Равносторонний треугольник вписан в окружность радиуса 5 см

Геометрия | 5 — 9 классы

Правильный треугольник вписан в окружность радиуса 5 см.

Определите радиус окружности, вписанной в этот треуг — к.

Зная радиус описанной окружности, найдем длину стороны треугольника : а = R * корень из 3 = 5корней из 3(см).

Сторона правильного треугольника, в который вписана окружность(через радиус вписанной окружности) : а = r * 2корня из 3 ; = &gt ; r = а / 2корня из 3 = 5 / 2 = 2, 5(см).

Видео:Равносторонний треугольник в окружностиСкачать

Прямоугольный треугольник вписан в окружность радиуса 5см в треугольник вписана окружность радиуса 1см найдите площадь треугольника?

Прямоугольный треугольник вписан в окружность радиуса 5см в треугольник вписана окружность радиуса 1см найдите площадь треугольника.

Видео:Окружность вписана в равносторонний треугольник, найти радиусСкачать

Правильный треугольник вписан в окружность, радиуса 6 см ?

Правильный треугольник вписан в окружность, радиуса 6 см .

Найдите периметр треугольника и радиус вписанной в него окружности.

Видео:Задание № 1088 — Геометрия 9 класс (Атанасян)Скачать

В правильный треугольник со стороной а вписана окружность, найдите радиус?

В правильный треугольник со стороной а вписана окружность, найдите радиус.

Видео:ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

Радиус окружности описанной около правильного треугольника равен 6см найдите радиус окружности вписанной в него?

Радиус окружности описанной около правильного треугольника равен 6см найдите радиус окружности вписанной в него.

Видео:Задание 16 ОГЭ по математике. Окружность вписана в равносторонний треугольник.Скачать

В окружность вписан правильный шестиугольник?

В окружность вписан правильный шестиугольник.

В него вписана окружность, в которую вписан правильный треугольник.

Найдите радиус большей окружности, если сторона треугольника равна 1 см.

Видео:15 задание треугольники огэ по математике / маттаймСкачать

В окружность с радиусом R, вписан правильный треугольник?

В окружность с радиусом R, вписан правильный треугольник.

Найдите радиус окружности, вписанной в этот треугольник.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Радиус окружности, описанной около правильного треугольника, равен 8см?

Радиус окружности, описанной около правильного треугольника, равен 8см.

Найдите радиус вписанной окружности.

Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Правильный треугольник со стороной см вписан в окружность?

Правильный треугольник со стороной см вписан в окружность.

Найдите радиус этой окружности.

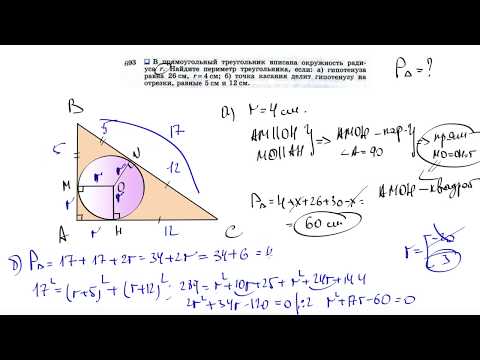
Видео:№693. В прямоугольный треугольник вписана окружность радиуса r. Найдите периметр треугольника,Скачать

В окружности радиуса 2 корень из 3 вписан правильный треугольник?

В окружности радиуса 2 корень из 3 вписан правильный треугольник.

Найдите радиус окружности, вписанной в данный треугольник.

Видео:Равносторонний треугольник вписан в окружность. Найти площадь меньшего сегмента.Скачать

Правильный треугольник вписан в окружность радиуса 5см?

Правильный треугольник вписан в окружность радиуса 5см.

Определите радиус окружности, вписанной в этот треугольник.

На этой странице сайта вы найдете ответы на вопрос Правильный треугольник вписан в окружность радиуса 5 см?, относящийся к категории Геометрия. Сложность вопроса соответствует базовым знаниям учеников 5 — 9 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.

В треугольнике АВС∠С = 90°, ∠А = 42°, ∠В = 90 — 42 = 48°. СН — высота, СЕ — биссектриса. ∠ЕСН = ? Высота прямоугольного треугольника делит его на два подобных треугольника, каждый из которых подобен исходному, значит∠АСН = ∠СВА = 48°. ∠АСЕ = 90 /..

(2, 3, 4), (2, 4, 5), (2, 5, 6) (3, 4, 5), (3, 4, 6), (3, 5, 6) (4, 5, 6) 7 треугольников.

ВО = ОС = АО = ОД = 7, 5см Р треугольника АОВ = ВО + АО + АВ = 7, 5 + 7, 5 + 4 = 19.

Треугольник не только прямоугольный , но и с равными катетами, равнобедренный, значит углы при основании 45тангенс 45 = 1.

Катет против угла в 30 градусов равен половине гипотенузы. Этот же катет прилежит к углу в 60 градусов. Гипотенуза т. О. будет 4 * 2 = 8.

По теореме синусов : x / sin(30°) = 12 / sin(90°) = > = >x / sin(30°) = 12 = > = >x = 12 * sin(30°) = > = >x = 12 * 0, 5 = > = >x = 6 (см) ; Ответ : 6 см.

Сумма угла 1 и 2 180 градусов. Угол 2 равен 180 — 125 = 55 градусов. Сумма всех углов 1, 2, 3 и 4 равна 360 градусов. Углы 1 и 3 одинаковые, значит угол 3 равен 125 градусов. Угол 4 — это или 360 — 125 — 125 — 55 = 55 градусов, или аналогично с у..

В результате обмена веществ организм получает энергию для своих жизненных процессов (энергетический обмен) и материал для построения и обновления клеток. (пластические процессы).

Решение задания приложено с поправкой.

Только одно верное утверждение : любые два равносторонние треугольники подобны. Так как все 3 угла равностороннего треугольника равны 60 градусов, а если у двух треугольников два угла равны, то такие треугольники подобны.

Видео:Построение равностронего треугольника.Скачать

Треугольник вписан в окружность радиуса 5 см

Видео:Шестнадцатое задание ОГЭ по математике (1) #огэ #огэ2023 #огэматематика #огэпоматематике #математикаСкачать

Треугольник вписанный в окружность

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:Равносторонний треугольник. Описанная окружностьСкачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = frac ab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Видео:Равносторонний треугольникСкачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Видео:Как легко решить задачу 17 по ОГЭСкачать

Нахождение радиуса вписанной в треугольник окружности

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в произвольный (любой), прямоугольный, равнобедренный или равносторонний треугольник. Также разберем примеры решения задач для закрепления представленного теоретического материала.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Формулы вычисления радиуса вписанной окружности

Произвольный треугольник

Радиус окружности, вписанной в любой треугольник, равняется удвоенной площади треугольника, деленной на его периметр.

где a, b, c – стороны треугольника, S – его площадь.

Прямоугольный треугольник

Радиус окружности, вписанной в прямоугольный треугольник, равняется дроби, в числителе которого сумма катетов минус гипотенуза, в знаменателе – число 2.

где a и b – катеты, c – гипотенуза треугольника.

Равнобедренный треугольник

Радиус вписанной в равнобедренный треугольник окружности вычисляется по формуле ниже:

где a – боковые стороны, b – основание треугольника.

Равносторонний треугольник

Радиус вписанной в правильный (равносторонний) треугольник окружности рассчитывается следующим образом:

где a – сторона треугольника.

Видео:2065 радиус окружности вписанной в правильный треугольник равен 29 Найдите высоту этого треугольникаСкачать

Примеры задач

Задание 1
Дан треугольник со сторонами 5, 7 и 10 см. Вычислите радиус вписанной в него окружности.

Решение
Сперва вычислим площадь треугольника. Для этого применим формулу Герона:

Остается только применить соответствующую формулу для вычисления радиуса круга:

Задание 2
Боковые стороны равнобедренного треугольника равны 16 см, а основание 7 см. Найдите радиус вписанной в фигуру окружности.

Решение
Воспользуемся подходящей формулой, подставив в нее известные значения:

Видео:Как разделить окружность на 3 равные части или как вписать равнобедренный треугольник в окружностьСкачать

Найдите периметр прямоугольного треугольника, вписанного в окружность радиуса 7,5 см, если один из катетов равен 9 см.

Ваш ответ

решение вопроса

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,937
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

№ 22. Найдите площадь правильного треугольника, вписанного вкруг радиуса 5.

Решебник по геометрии за 9 класс (А.В.Погорелов, 2001 год),
задача №22
к главе «§14. Площади фигур».

Выделите её мышкой и нажмите CTRL + ENTER

Большое спасибо всем, кто помогает делать сайт лучше! =)

Нажмите на значок глаза возле рекламного блока, и блоки станут менее заметны. Работает до перезагрузки страницы.