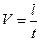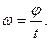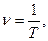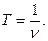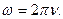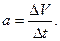Равнопеременное движение по окружности

1.Равномерное движение по окружности

2.Угловая скорость вращательного движения.

5.Связь линейной скорости с угловой.

7.Равнопеременное движение по окружности.

8.Угловое ускорение в равнопеременном движении по окружности.

10.Закон равноускоренного движения по окружности.

11. Средняя угловая скорость в равноускоренном движении по окружности.

12.Формулы, устанавливающие связь между угловой скоростью, угловым ускорением и углом поворота в равноускоренном движении по окружности.

1.Равномерное движение по окружности – движение, при котором материальная точка за равные интервалы времени проходит равные отрезки дуги окружности, т.е. точка движется по окружности с постоянной по модулю скоростью. В этом случае скорость равна отношению дуги окружности, пройденной точкой ко времени движения, т.е.

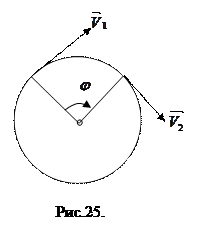
и называется линейной скоростью движения по окружности.

Как и в криволинейном движении вектор скорости направлен по касательной к окружности в направлении движения (Рис.25).

2. Угловая скорость в равномерном движении по окружности – отношение угла поворота радиуса ко времени поворота:

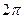
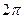
В равномерном движении по окружности угловая скорость постоянна. В системе СИ угловая скорость измеряется в(рад/c). Один радиан – рад это центральный угол, стягивающий дугу окружности длиной равной радиусу. Полный угол содержит радиан, т.е. за один оборот радиус поворачивается на угол радиан.

3. Период вращения – интервал времени Т, в течении которого материальная точка совершает один полный оборот. В системе СИ период измеряется в секундах.

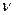
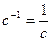
4. Частота вращения – число оборотов , совершаемых за одну секунду. В системе СИ частота измеряется в герцах ( 1Гц = 1 ) . Один герц – частота, при которой за одну секунду совершается один оборот. Легко сообразить, что

Если за время t точка совершает n оборотов по окружности то .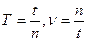

Зная период и частоту вращения, угловую скорость можно вычислять по формуле:

или

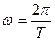
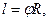
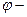
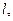
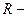
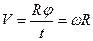
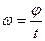
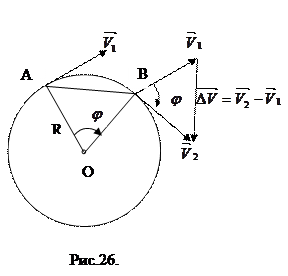
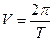
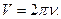
5 Связь линейной скорости с угловой. Длина дуги окружности равна где центральный угол, выраженный в радианах, стягивающий дугу радиус окружности. Теперь линейную скорость запишем в виде

, где .

Часто бывает удобно использовать формулы: или Угловую скорость часто называют циклической частотой, а частоту линейной частотой.

6. Центростремительное ускорение. В равномерном движении по окружности модуль скорости остаётся неизменным , а направление её непрерывно меняется (Рис.26). Это значит, что тело, движущееся равномерно по окружности, испытывает ускорение, которое направлено к центру и называется центростремительным ускорением.

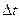
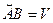
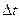
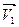
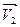
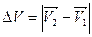
Пусть за промежуток времени прошло путь равный дуге окружности . Перенесём вектор , оставляя его параллельным самому себе, так чтобы его начало совпало с началом вектора в точке В. Модуль изменения скорости равен , а модуль центростремительного ускорения равен

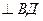
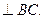
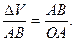
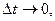
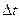
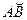
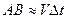
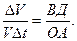
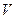
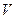
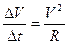
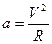
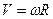
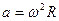
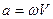
На Рис.26 треугольники АОВ и ДВС равнобедренные и углы при вершинах О и В равны, как углы с взаимно перпендикулярными сторонами АО и ОВ Это значит, что треугольники АОВ и ДВС подобные. Следовательно Если то есть интервал времени принимает сколь угодно малые значения, то дугу можно приближенно считать равной хорде АВ, т.е. . Поэтому можем записать Учитывая, что ВД= , ОА=R получим Умножая обе части последнего равенства на , получим и далее выражение для модуля центростремительного ускорения в равномерном движении по окружности: . Учитывая, что получим две часто применяемые формулы:

, .

Итак, в равномерном движении по окружности центростремительное ускорение постоянно по модулю.

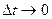
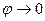
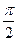
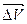
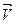
Легко сообразить, что в пределе при , угол . Это значит, что углы при основании ДС треугольника ДВС стремятся значению , а вектор изменения скорости становится перпендикулярным к вектору скорости , т.е. направлен по радиусу к центру окружности.

7. Равнопеременное движение по окружности – движение по окружности, при котором за равные интервалы времени угловая скорость изменяется на одну и ту же величину.

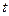
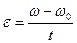
8. Угловое ускорение в равнопеременном движении по окружности – отношение изменения угловой скорости к интервалу времени , в течении которого это изменение произошло, т.е.

,

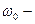
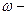
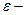
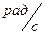
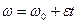
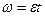
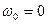
где начальное значение угловой скорости, конечное значение угловой скорости, угловое ускорение, в системе СИ измеряется в . Из последнего равенства получим формулы для вычисления угловой скорости

и , если .

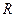
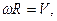
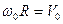
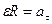
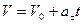
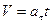
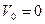
Умножая обе части этих равенств на и учитывая, что , — тангенциальное ускорение, т.е. ускорение, направленное по касательной к окружности , получим формулы для вычисления линейной скорости:

и , если .

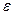
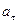
9. Тангенциальное ускорение численно равно изменению скорости в единицу времени и направлено вдоль касательной к окружности. Если >0, >0, то движение равноускоренное. Если

Дата добавления: 2015-08-08 ; просмотров: 17103 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Кинематика. Равнопеременное движение по окружностиСкачать

I. Механика

Видео:Физика - движение по окружностиСкачать

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Видео:Физика | Равномерное движение по окружностиСкачать

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Видео:Равноускоренное движение по окружностиСкачать

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Видео:Центростремительное ускорение. 9 класс.Скачать

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Видео:Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Видео:Вращательное движение. 10 класс.Скачать

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Равнопеременное движение.

Равнопеременным движением точки называется движение, при котором тело за равные промежутки времени изменяется одинаково.

Под равнопеременным движением понимают: равноускоренное движение (когда модуль скорости увеличивается, т. е. ускорение параллельно скорости — ), и равнозамедленное движение (когда модуль скорости уменьшается, т. е. ускорение антипараллельно скорости — ).

Видео:О терминах равноускоренное и равнозамедленное движениеСкачать

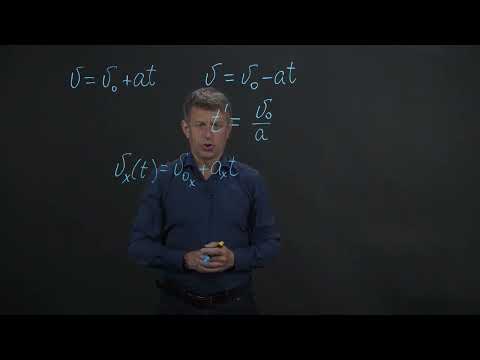
Ускорение и скорость при равнопеременном движении.

Ускорение равнопеременного движения — физическая величина, характеризующая быстроту изменения скорости, численно равная отношению вектора изменения скорости к промежутку времени, в течение которого это изменение произошло.

Спроектировав ускорение и скорость на направление движения, получим следующий вид уравнения:

где υ₀ — скорость в начальный момент времени, принятый за нуль; υ – текущее значение скорости. При определении ускорения тела из состояния покоя (равноускоренное движение, где начальная скорость υ₀ = 0) формула имеет вид:

При равнозамедленном движении, когда нулю равна не начальная, а конечная скорость, формула принимает вид:

Из первой формулы можно вывести формулу скорости:

📹 Видео

Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

Криволинейное, равномерное движение материальной точки по окружности. Практическая часть. 9 класс.Скачать

Равноускоренное движение по окружности. Видеоурок 51. Физика 10 классСкачать

Урок 89. Движение по окружности (ч.1)Скачать

Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать

УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Равнопеременное (равноускоренное) движениеСкачать