Равномерное распределение точек в окружности (7 видео)

Распределять точки по кругу как можно равномерно

Содержание

Описание проблемы
Примеры
Предыдущая попытка
Обновление: завершенный алгоритм:
ОТВЕТЫ
Ответ 1
Ответ 2
Ответ 3
Ответ 4
Ответ 5
Ответ 6
Ответ 7
Ответ 8
Генерировать случайную точку внутри круга (равномерно)
21 ответов
как создать случайную точку в пределах круга радиуса R:
почему sqrt(random()) ?
Создать случайную точку внутри круга (равномерно)
Как создать случайную точку внутри круга радиуса R :
Зачем sqrt(random()) ?
🔥 Видео

Видео:Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

Описание проблемы

У меня есть следующая проблема: у меня есть круг с определенным числом (ноль или более) точек на нем. Эти позиции фиксированы. Теперь я должен расположить еще один набор точек на круге, например, все точки вместе равномерно распределены по кругу, насколько это возможно.

Теперь моя цель — разработать алгоритм, содержащий список углов (представляющих неподвижные точки) и значение int (представляющее количество дополнительных точек) и снова возвращать список углов (содержащих только углы, в которых дополнительные пункты должны лежать).

Точки не должны быть действительно равномерно распределены (все одинаковое расстояние друг от друга), а скорее равномерно, насколько это возможно. Идеальное решение может не существовать большую часть времени, поскольку определенные точки фиксированы.

Диапазон всех углов лежит между -pi и + pi.

Видео:Равномерное распределение точек в кругуСкачать

Примеры

Некоторые примеры того, что я пытаюсь архивировать:

В этом последнем примере нужно вернуть что-то вроде: одна точка должна установить прямо между -pi * 3/4 и -pi/4, то есть: -pi/2 и распределить остальные 5 точек между -pi/4 и + pi (помните, что это круг, поэтому в этом случае -pi = + pi):

Видео:Равномерное распределениеСкачать

Предыдущая попытка

Я начал с рекурсивного алгоритма, который сначала ищет самый большой интервал между двумя точками и устанавливает новую точку прямо между ними. Однако он не дает удовлетворительные результаты. Рассмотрим, например, эту конфигурацию с двумя точками, которые необходимо вставить:

Не очень хорошее решение, так как оно могло быть гораздо лучше распределено (см. выше: -pi/6 и + pi/6).

Извините за длинный вопрос, надеюсь, вы понимаете, что я хочу архивировать.

Мне не нужен полный рабочий алгоритм, а правильная идея его разработки. Может быть, какой-нибудь псевдокод, если хотите. Был бы очень благодарен за некоторые намеки, чтобы подтолкнуть меня в правильном направлении. Спасибо заранее!

Видео:Физика | Равномерное движение по окружностиСкачать

Обновление: завершенный алгоритм:

Спасибо всем за ваши ответы! Мне показалось, что мне просто нужна была не жадная версия моего уже существующего алгоритма. Мне очень понравилась идея haydenmuhls, чтобы немного упростить проблему, инкапсулируя класс интервалов/сегментов:

Это делает алгоритм невероятно простым и понятным:

Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

ОТВЕТЫ

Ответ 1

Вы можете использовать объект Interval. Интервал представляет собой дугу круга между двумя исходными неподвижными точками.

Ниже приведен только псевдокод. Не ожидайте, что он будет работать где угодно.

Создайте список этих объектов, соответствующий интервалам между точками вашего круга. Каждый раз, когда вы добавляете точку, выберите интервал с наибольшим next_sub_length(). Когда вы закончите, нетрудно восстановить новый круг.

Это должно дать вам интервал с максимально возможным минимальным интервалом. То есть, если вы забьете решение по длине наименьшего интервала, это даст вам самый высокий балл. Я думаю, что вы стреляли.

Изменить: Просто понял, что вы специально задали об этом в Python. Я довольно Python n00b, но вы должны легко преобразовать его в объект Python, хотя вам не нужны геттеры, поскольку все в Python является общедоступным.

Ответ 2

Предположим, что у вас уже есть теги M , а еще нужно добавить N . Если все точки были равномерно распределены, у вас были бы пробелы 2*pi/(N+M) между ними. Итак, если вы нарезаете точки M , чтобы дать M сегменты угла, вы можете, конечно, поместить точки в сегмент (равномерно распределенные друг от друга), пока пространство не станет меньше или равно 2*pi/(N+M) .

Итак, если длина сегмента L , тогда вы должны поместить в него floor(L*(N+M)/(2*pi)) — 1 .

Теперь у вас останутся некоторые моменты. Разделите сегменты на расстояние, которое вы имели бы между точками, если бы добавилась еще одна точка. На самом деле добавьте точку в сегмент с наименьшим рангом. Повторно вставьте это в свой отсортированный список и сделайте это снова, пока не закончите очки.

Так как каждый раз вы помещаете точку в сегмент, где результат будет как можно более широким, а пространство между точками не зависит от того, в каком порядке вы добавили их, вы получите оптимальный интервал.

(Edit: где «оптимальный» означает «максимальное минимальное расстояние между точками», т.е. избегая наихудшего сценария точек сверху друг друга как можно лучше.)

(Редактирование: я надеюсь, что ясно, что идея состоит в том, чтобы решить, сколько точек входит в каждый сегмент, а затем только в самом конце, после того, как все были решены, вы размещаете их одинаково в каждом сегменте. )

Ответ 3

Предположим, что интервалы между точками равны a_1. a_n. Затем, если мы разделим каждый сегмент на куски минимального размера d, мы можем поместить floor(a_i/d) — 1 в сегменте. Это означает, что sum(floor(a/d) for a in interval_lengths) должно быть больше или равно n + s , где n — количество точек, которые мы хотим добавить, а s — количество точек, которые уже есть. Мы хотим выбрать d как можно больше, вероятно, лучше всего выполнить двоичный поиск наилучшего d.

Как только мы выбрали d, просто перейдите через каждый сегмент, добавив точки каждые d градусов, пока в сегменте не останется меньше 2 d градусов

Изменить все, что вам нужно, — найти d таким образом, чтобы sum(floor(a/d) for a in interval_lengths) == n + s , а затем назначить floor(a_i/d) — 1 сегментировать я каждые a_i/(floor(a_i/d) — 1) градусов. Двоичный поиск найдет это быстро.

Дальнейшее редактирование

Вот код для поиска d

Ответ 4

Сначала мы переопределяем термин следующим образом: Найдите такое распределение N точек, что длина минимального расстояния между любой из двух точек этих и предопределенных M максимальна. Поэтому ваша задача — найти этот максимум минимальной длины. Назовите его L У вас есть длина M существующих сегментов, предположите, что они хранятся в списке s . Поэтому, если эта длина L в первую очередь

и максимальное количество дополнительных точек

Итак, вы можете найти оптимальный L, используя двоичный поиск, начинающий минимум L = 0 и максимум L = min (s) и проверяя условие, если сумма (ls/L -1 для ls в s) >= N. Тогда для каждого сегмента s [i] вы можете просто поместить s [i]/L -1 точек равномерно. Я думаю, что это оптимальное решение.

Обновлено. В min(s) > L был недостаток. Это было достаточно хорошо для переопределенного термина, но ошибка для оригинала. Я изменил это условие на max(s) > L . Также добавлено пропускание сегментов меньше L в двоичном поиске. Вот полный обновленный код:

Ответ 5

Вы никогда не говорили точно, как точно измеряется равномерное расстояние. Общая среднеквадратичная дисперсия размера интервала от идеально расположенных интервалов размеров или что-то еще?

Если вы посмотрите на какой-либо конкретный открытый интервал в начале, я считаю, что оптимальное решение, в котором k точек в этом интервале будет всегда равномерно распределять их. Поэтому проблема сводится к выбору точек отсечения для того, для чего нужен минимальный размер интервала, чтобы получить определенное количество промежуточных точек. Когда закончите, если у вас недостаточно очков для распространения, отбросьте одну точку с каждого интервала от самого большого до самого маленького и повторите, пока не получите что-то разумное.

Я не уверен, что лучший способ выбрать отсечки.

Ответ 6

Я предлагаю рассмотреть эту проблему либо как:

Обернутая линия — позволяет легко определить расстояние между точками, затем перекругнуть круг

Рассмотрим углы между точками и центром круга, а не дугой. Опять же, это упрощает позиционирование новых точек и, возможно, является более легким кандидатом для повторного сопоставления точек окружности. Найдите все углы между уже размещенными точками, затем разделите наибольшую (или аналогичную) пополам и поместите новую точку в соответствующую точку на краю круга.

Ответ 7

Ответ 8

У меня есть функция, называемая «условие», которая принимает два аргумента — числитель (const) и знаменатель (pass-by-ref). Он либо «вырастает», либо «сжимает» значение знаменателя до тех пор, пока целое число «знаменателей» не войдет в числитель, т.е. Так, что числитель/знаменатель является целым числом.

будет ли знаменатель выращен или сокращен, зависит от того, какой из них приведет к его изменению на меньшую величину.

Установите числитель на 2 * pi и знаменатель на любой тип близкого расстояния, который вы хотите, и вы должны иметь довольно близкое к равномерному распределению.

Обратите внимание, что у меня также есть функция «сравнить», которая сравнивает два удвоения для равенства в пределах определенного допуска.

то функция условия

Надеюсь, что это поможет, я знаю, что этот маленький алгоритм пришел очень кстати для меня несколько раз.

Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Генерировать случайную точку внутри круга (равномерно)

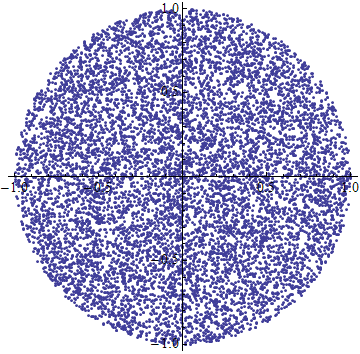
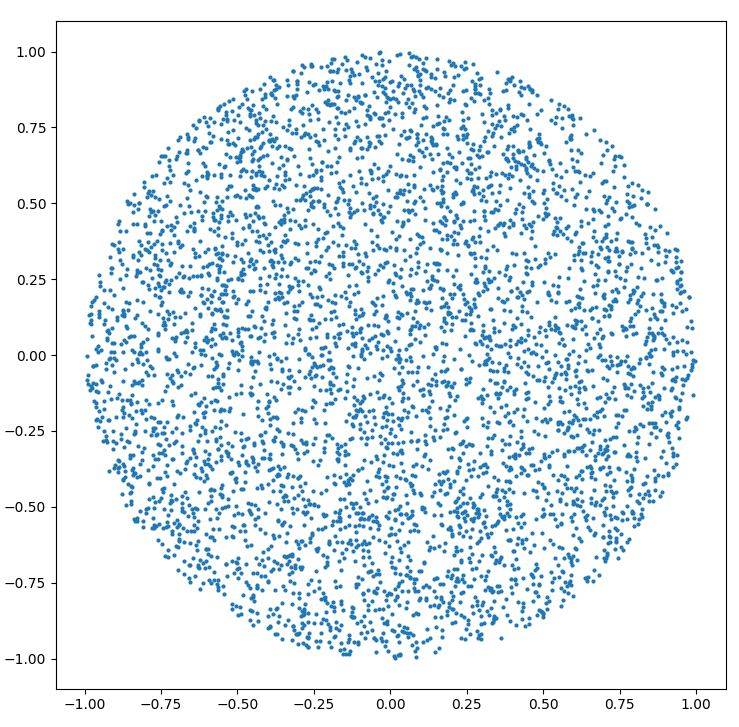
Мне нужно создать равномерно случайную точку в пределах круга радиуса R.

Я понимаю, что просто выбирая равномерно случайный угол в интервале [0 . 2π) и равномерно случайный радиус в интервале (0 . R) Я бы закончил с большим количеством точек к центру, так как для двух заданных радиусов точки меньшего радиуса будут ближе друг к другу, чем для точек большего радиуса.

Я нашел запись в блоге это здесьЯ бы очень хотел понять, откуда он получает (2/R 2 )×r и как он получает окончательное решение.

обновление: через 7 лет после публикации этого вопроса я все еще не получил удовлетворительного ответа на фактический вопрос о математике алгоритма квадратного корня. Так я провел день сам пишу ответ. ссылка на мой ответ.

Видео:"Парадоксальное" среднее расстояние между точками на окружностиСкачать

21 ответов

давайте как Архимед бы.

как мы можем генерировать точку равномерно в треугольнике ABC, где / AB / =|BC/? Давайте упростим это, распространившись на параллелограмм ABCD. Легко генерировать точки равномерно в ABCD. Мы равномерно выбираем случайную точку X на AB и Y на BC и выбираем Z такой, что XBYZ является параллелограммом. Чтобы получить равномерно выбранную точку в исходном треугольнике, мы просто складываем все точки, которые появляются в АЦП, обратно в ABC вдоль ПЕРЕМЕННЫЙ ТОК.

Теперь рассмотрим кругу. В пределе мы можем думать о нем как о бесконечном множестве изоцелевых треугольников ABC с B в начале и A и C на окружности, исчезающе близких друг к другу. Мы можем выбрать один из этих треугольников, просто выбрав угол тета. Поэтому теперь нам нужно сгенерировать расстояние от центра, выбрав точку в Щепке ABC. Опять же, распространитесь на ABCD, где D теперь вдвое больше радиуса от центра круга.

выбор случайной точки в ABCD используя описанный выше метод. Выберите случайную точку на AB. Равномерно выберите случайную точку на BC. То есть. выберите пару случайных чисел X и y равномерно на [0, R], дающих расстояния от центра. Наш треугольник представляет собой тонкую полоску, поэтому AB и BC по существу параллельны. Таким образом, точка Z-это просто расстояние x+y от начала координат. Если x+y>R, мы складываемся обратно.

вот полный алгоритм для R=1. Надеюсь, вы согласитесь, что все очень просто. Он использует trig, но вы можете дать гарантию на сколько времени он будет возьмите, а сколько random() вызывает его потребности, не похож на забор сброса.

вот он в Mathematica.

Видео:Криволинейное, равномерное движение материальной точки по окружности. Практическая часть. 9 класс.Скачать

как создать случайную точку в пределах круга радиуса R:

(если random() дает значение между 0 и 1 равновероятно)

если вы хотите преобразовать это в Декартовые координаты, вы можете сделать

Видео:Точки на числовой окружностиСкачать

почему sqrt(random()) ?

давайте посмотрим на математику, которая приводит к sqrt(random()) . Предположим для простоты, что мы работаем с единичным кругом, т. е. R = 1.

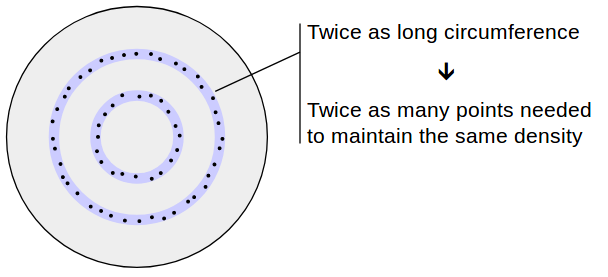
среднее расстояние между точками должно быть одинаковым независимо от того, как далеко от центра мы смотрим. Это означает, например, что, глядя на периметр круга с окружностью 2, мы должны найти в два раза больше точек, чем количество точек на периметре круга с окружностью 1.

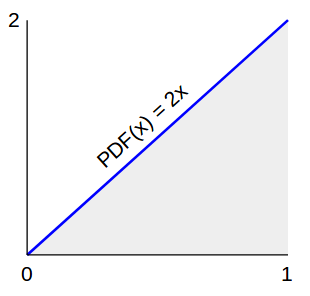
С длины окружности (2πr) растет линейно с r, из этого следует, что количество случайных точек должно линейно расти с r. Другими словами, желаемое функция плотности вероятности (PDF) растет линейно. Поскольку PDF должен иметь площадь равную 1, а максимальный радиус равен 1, то есть

таким образом, мы знаем, как должна выглядеть желаемая плотность наших случайных значений. Теперь:как мы генерируем такое случайное значение, когда все мы имеют равномерное случайное значение между 0 и 1?

из PDF создайте кумулятивная функция распределения (CDF)
зеркало это вдоль y = x
применить полученную функцию к равномерному значению от 0 до 1.

звучит сложно? Позвольте мне вставить желтую коробку с небольшим количеством боковой путь, который передает интуицию:

Предположим, мы хотим создать случайную точку со следующим распределением:

1/5 из пунктов равномерно между 1 и 2, и
4/5 точек равномерно между 2 и 3.

CDF, как следует из названия, является накопительной версией PDF. Интуитивно: Пока PDF (x) описывает количество случайных значений на x, CDF (x) описывает количество случайных значений меньше, чем x.

в этом случае CDF будет выглядеть так:

чтобы увидеть, как это полезно, представим, что мы стреляем пулями слева направо на равномерно распределенных высот. Когда пули попадают в линию, они падают на землю:—10—>

посмотрите, как плотность пуль на земле соответствует нашему желаемому распределению! Мы почти на месте!

проблема в том, что для этой функции y ось —выход и x ось —вход. Мы можем только «стрелять пулями с земли прямо вверх»! Нам нужна обратная функция!

вот почему мы отражаем все это; x становится y и y становится x:

мы называем это CDF -1 . Чтобы получить значения в соответствии с желаемым распределением, мы используем CDF -1 (random ()).

. Итак, вернемся к генерации случайных значений радиуса, где наш PDF равен 2x.

Шаг 1: Создайте CDF:

Поскольку мы работаем с reals, CDF выражается как Интеграл PDF.

Шаг 2: Зеркало CDF вдоль y = x:

математически это сводится к замене x и y и решения для y:

Шаг 3: примените полученную функцию к равномерному значению между 0 и 1

CDF -1 (random ()) = √random ()

что мы намеревались вывести: -)

вот быстрое и простое решение.

выбрать два случайных числа в диапазоне (0, 1), а именно a и b . Если b , поменять их местами. Ваша точка зрения (b*R*cos(2*pi*a/b), b*R*sin(2*pi*a/b)) .

вы можете думать об этом решении следующим образом. Если взять круг, вырезать его, а затем выпрямить, получится прямоугольный треугольник. Масштабируйте этот треугольник вниз, и у вас будет треугольник из (0, 0) до (1, 0) to (1, 1) и (0, 0) . Все эти преобразования измените плотность равномерно. То, что вы сделали, — это равномерно выбрать случайную точку в треугольнике и обратить процесс, чтобы получить точку в круге.

обратите внимание на плотность точки пропорционально обратному квадрату радиуса, следовательно, вместо выбора r С [0, r_max] С [0, r_max^2] , затем вычислите свои координаты как:

это даст вам равномерное распределение точек на диске.

подумайте об этом таким образом. Если у вас есть прямоугольник, где одна ось-радиус, а одна-угол, и вы берете точки внутри этого прямоугольника, которые находятся рядом с радиусом 0. Все они будут падать очень близко к началу (то есть близко друг к другу по кругу.) Однако точки вблизи радиуса R все они будут падать вблизи края круга (то есть далеко друг от друга.)

Это может дать вам некоторое представление о том, почему вы получаете такое поведение.

фактор это выведено на этой ссылке говорит вам, сколько соответствующей области в прямоугольнике необходимо настроить, чтобы не зависеть от радиуса, как только он сопоставлен с кругом.

Edit: Итак, то, что он пишет в ссылке, которую вы разделяете, — «это достаточно легко сделать, вычисляя обратное кумулятивное распределение, и мы получаем для r:».

основная предпосылка здесь заключается в том, что вы можете создать переменную с желаемым распределением из равномерного, сопоставив равномерное обратным функция кумулятивной функции распределения желаемой функции плотности вероятности. Почему? Просто примите это как должное, но это факт.

вот мой somehwat интуитивное объяснение математики. Функция плотности f (r) по отношению к r должна быть пропорциональна самой r. Понимание этого факта является частью любой основной книги по исчислению. См. разделы об элементах полярной области. Некоторые другие плакаты упоминали об этом.

поэтому мы назовем его f (r) = C*r;

это, оказывается, большая часть работы. Теперь, поскольку F(r) должна быть плотностью вероятности, вы можете легко увидеть,что, интегрируя f (r) через интервал (0, R), вы получите, что C = 2/R^2 (это упражнение для читателя.)

таким образом, f(r) = 2*r/r^2

OK, так вот как вы получаете формулу в ссылке.

тогда конечная часть идет от равномерной случайной величины u в (0,1), которую вы должны отобразить обратной функцией кумулятивного функция распределения от этой желаемой плотности f (r). Чтобы понять, почему это так, вам нужно найти расширенный текст вероятности, такой как Papoulis, вероятно (или вывести его самостоятельно.)

интегрируя f (r), вы получаете F(r) = r^2/R^2

чтобы найти обратную функцию этого, вы устанавливаете u = r^2 / R^2, а затем решаете для r, что дает вам r = R * sqrt (u)

это полностью имеет смысл интуитивно тоже, u = 0 должно соответствовать r = 0. Кроме того, U = 1 shoudl map to r = R. Также, он идет по функции квадратного корня, которая имеет смысл и соответствует ссылке.

Это действительно зависит от того, что вы подразумеваете под ‘абсолютно случайная’. Это тонкий момент, и вы можете прочитать больше об этом на странице wiki здесь:http://en.wikipedia.org/wiki/Bertrand_paradox_%28probability%29, где одна и та же проблема, давая разные интерпретации «равномерно случайным» дает разные ответы!

в зависимости от того, как вы выбираете точки, распределение может варьироваться, даже если они равномерно случайны в некоторые чувство.

похоже, что запись в блоге пытается сделать ее равномерно случайной в следующем смысле: если вы берете подпругу круга с тем же центром, то вероятность того, что точка падает в этой области, пропорциональна площади области. Это, я считаю, пытается следовать теперь стандартной интерпретации «равномерно случайных» для 2D-областей с области, определенные на них: вероятность падения точки в любой области (с областью хорошо defined) пропорциональна площади этой области.

причина, по которой наивное решение не работает, заключается в том, что оно дает более высокую плотность вероятности точкам ближе к центру круга. Другими словами, окружность с радиусом r/2 имеет вероятность r/2 получить выбранную в ней точку, но имеет площадь (количество точек) pi*r^2/4.

поэтому мы хотим, чтобы плотность вероятности радиуса имела следующее свойство:

вероятность выбора радиуса меньшего или равного заданному r должна быть пропорциональна площадь окружности с радиусом r. (потому что мы хотим иметь равномерное распределение по точкам, а большие площади означают больше точек)

другими словами, мы хотим, чтобы вероятность выбора радиуса между [0, r] была равна его доле от общей площади круга. Общая площадь окружности равна pi * R^2, а площадь окружности с радиусом r равна pi * r^2. Таким образом,мы хотели бы, чтобы вероятность выбора радиуса между [0, r] была (pi*r^2)/(pi*R^2) = r^2/R^2.

теперь приходит математика:

вероятность выбора радиуса между [0, r] является интегралом от p(r) dr от 0 до r (это просто потому, что мы добавляем все вероятности меньших радиусов). Таким образом, мы хотим Интеграл(p(r)dr) = r^2/R^2. Мы можем ясно видеть, что R^2 является константой, поэтому все, что нам нужно сделать, это выяснить, какой p(r), когда он интегрирован, даст нам что-то вроде r^2. Ответ явно Р * постоянный. Интеграл (R * константа dr) = r^2/2 * константа. Это должно быть равно r^2/R^2, поэтому Константа = 2 / R^2. Таким образом, у вас есть распределение вероятностей p(r) = r * 2/R^2

Примечание:

вот мой код Python для генерации num случайные точки из окружности радиуса rad :

пусть ρ (радиус) и φ (Азимут) — две случайные величины, соответствующие полярным координатам произвольной точки внутри круга. Если точки распределены равномерно, то какова функция распределения ρ и φ?

где S1 и S0-площади круга радиус r и R соответственно. Таким образом, CDF можно дать как:

обратите внимание, что для r=1 случайная величина sqrt(X), где X равномерна на [0, 1), имеет этот точный CDF (потому что P[sqrt(X)

распределение φ, очевидно, равномерно от 0 до 2*π. Теперь вы можете создавать случайные полярные координаты и преобразовывать их в Декартовые, используя тригонометрические уравнения:

не могу сопротивляться сообщение кода python для R=1.

вы получите

Видео:Математика это не ИсламСкачать

Создать случайную точку внутри круга (равномерно)

Мне нужно создать равномерно случайную точку в радиусе круга R .

Я понимаю это, просто выбирая равномерно случайный угол в интервале [0 . 2π) и равномерно случайный радиус в интервале (0 . R ), я получу больше точек к центру, поскольку для двух данных радиусы, точки в меньшем радиусе будут ближе друг к другу, чем для точек в большем радиусе.

Я нашел запись в блоге по этому поводу здесь , но я не понимаю его рассуждения. Я полагаю, это правильно, но мне бы очень хотелось понять, откуда он получает (2 / R 2 ) × r и как он получает окончательное решение.

Обновление: 7 лет после публикации этого вопроса я все еще не получил удовлетворительного ответа на фактический вопрос относительно математики позади алгоритма квадратного корня. Так что я потратил день на написание ответа сам. Ссылка на мой ответ .

Давайте подойдем к этому, как Архимед.

Как мы можем сгенерировать точку равномерно в треугольнике ABC, где | AB | = | BC |? Давайте сделаем это проще, расширив параллелограмм ABCD. В ABCD легко генерировать точки равномерно. Мы равномерно выбираем случайную точку X на AB и Y на BC и выбираем Z таким, что XBYZ является параллелограммом. Чтобы получить равномерно выбранную точку в исходном треугольнике, мы просто складываем любые точки, которые появляются в АЦП, обратно в АВС вдоль АС.

Теперь рассмотрим круг. В пределе мы можем рассматривать его как бесконечно много равнобедренных треугольников ABC с B в начале координат и A и C на окружности, исчезающе близко друг к другу. Мы можем выбрать один из этих треугольников, просто выбрав угол тета. Итак, теперь нам нужно сгенерировать расстояние от центра, выбрав точку в полоске ABC. Снова продлим до ABCD, где D теперь в два раза больше радиуса от центра круга.

Выбрать случайную точку в ABCD легко, используя описанный выше метод. Выберите случайную точку на AB. Равномерно выбрать случайную точку на BC. То есть. Выберите пару случайных чисел x и y равномерно на [0, R], давая расстояния от центра. Наш треугольник является тонкой полоской, поэтому AB и BC по существу параллельны. Таким образом, точка Z — это просто расстояние x + y от начала координат. Если x + y> R, мы сбрасываем обратно.

Вот полный алгоритм для R = 1. Я надеюсь, вы согласны, что это довольно просто. Он использует триггер, но вы можете дать гарантию того, сколько времени это займет и сколько random() вызовов ему нужно, в отличие от выборки отклонения.

Вот это в Mathematica.

Видео:Геометрическая вероятностьСкачать

Как создать случайную точку внутри круга радиуса R :

(Предполагается, что random() дает значение между 0 и 1 равномерно)

Если вы хотите преобразовать это в декартовы координаты, вы можете сделать

Видео:Физика 10 Равномерное движение точки по окружностиСкачать

Зачем sqrt(random()) ?

Давайте посмотрим на математику, которая приводит к sqrt(random()) . Предположим для простоты, что мы работаем с единичным кругом, т.е. R = 1.

Среднее расстояние между точками должно быть одинаковым независимо от того, как далеко от центра мы смотрим. Это означает, например, что, глядя на периметр окружности с окружностью 2, мы должны найти вдвое больше точек, чем количество точек на периметре окружности с окружностью 1.

Поскольку окружность круга (2π r ) растет линейно с ростом r , отсюда следует, что число случайных точек должно расти линейно с ростом r . Другими словами, искомая функция плотности вероятности (PDF) растет линейно. Так как PDF должен иметь площадь, равную 1, а максимальный радиус равен 1, мы имеем

Итак, мы знаем, как должна выглядеть желаемая плотность наших случайных значений. Теперь: как мы можем генерировать такое случайное значение, когда все, что у нас есть, это равномерное случайное значение между 0 и 1?

Из PDF создайте накопительную функцию распределения (CDF)
Отразите это вдоль y = x
Примените полученную функцию к равномерному значению от 0 до 1.

Звучит сложно? Позвольте мне вставить цитату с небольшой боковой дорожкой, которая передает интуицию:

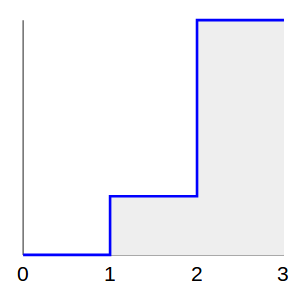
Предположим, мы хотим сгенерировать случайную точку со следующим распределением:

1/5 баллов равномерно между 1 и 2, и
4/5 баллов равномерно между 2 и 3.

CDF — это, как следует из названия, кумулятивная версия PDF. Интуитивно понятно: в то время как PDF ( x ) описывает количество случайных значений в точке x , CDF ( x ) описывает количество случайных значений меньше значения x .

В этом случае CDF будет выглядеть так:

Чтобы увидеть, как это полезно, представьте, что мы стреляем пулями слева направо на равномерно распределенных высотах. Когда пули попадают в линию, они падают на землю:

Посмотрите, как плотность пуль на земле соответствует нашему желаемому распределению! Мы почти там!

Проблема в том, что для этой функции ось y является выходной, а ось x является входной . Мы можем только «стрелять пулями прямо с земли»! Нам нужна обратная функция!

Вот почему мы отражаем все это; х становится у, а у становится х :

Мы называем это CDF -1 . Чтобы получить значения в соответствии с желаемым распределением, мы используем CDF -1 (random ()).

… Итак, вернемся к генерации случайных значений радиуса, где наш PDF равен 2 х .

Шаг 1: Создайте CDF: так

как мы работаем с реалами, CDF выражается как интеграл PDF.

Шаг 2: Зеркально отразите CDF вдоль y = x :

Математически это сводится к обмену x и y и решению для y :

Шаг 3: применить полученную функцию к равномерному значению от 0 до 1

CDF -1 (random ()) = √random ()

Что мы и собираемся извлечь 🙂

Вот быстрое и простое решение.

Выберите два случайных числа в диапазоне (0, 1), а именно a и b . Если b поменять их. Ваша точка зрения (b*R*cos(2*pi*a/b), b*R*sin(2*pi*a/b)) .

Вы можете думать об этом решении следующим образом. Если вы возьмете круг, обрежете его, а затем выпрямите, вы получите прямоугольный треугольник. Уменьшите этот треугольник, и вы получите треугольник от (0, 0) до (1, 0) до (1, 1) и обратно до (0, 0) . Все эти преобразования изменяют плотность равномерно. То, что вы сделали, равномерно выбрали случайную точку в треугольнике и полностью изменили процесс, чтобы получить точку в круге.

Обратите внимание на плотность точек пропорционально обратному квадрату радиуса, поэтому вместо того, чтобы выбирать r из [0, r_max] , выберите из [0, r_max^2] , а затем вычислите ваши координаты как:

Это даст вам равномерное распределение точек на диске.

Подумайте об этом таким образом. Если у вас есть прямоугольник, где одна ось является радиусом, а другая — углом, и вы берете точки внутри этого прямоугольника, которые близки к радиусу 0. Все они будут располагаться очень близко к началу координат (то есть близко друг к другу на окружности.) Однако, точки около радиуса R, все они будут падать около края круга (то есть далеко друг от друга).

Это может дать вам некоторое представление о том, почему вы получаете такое поведение.

Коэффициент, полученный по этой ссылке, говорит вам, сколько соответствующей области в прямоугольнике нужно отрегулировать, чтобы она не зависела от радиуса после его сопоставления с окружностью.

Редактировать: Итак, он пишет в ссылке, которой вы делитесь: «Это достаточно легко сделать, рассчитав обратное кумулятивному распределению, и мы получим для r:».

Основным условием здесь является то, что вы можете создать переменную с желаемым распределением из униформы, отобразив униформу с помощью обратной функции кумулятивной функции распределения желаемой функции плотности вероятности. Зачем? Просто пока принимайте это как должное, но это факт.

Вот мое интуитивное объяснение математики. Функция плотности f (r) по отношению к r должна быть пропорциональна самой r. Понимание этого факта является частью любой основной книги исчисления. Смотрите разделы об элементах полярной зоны. Некоторые другие постеры упоминали об этом.

Поэтому мы назовем это f (r) = C * r;

Это оказывается большая часть работы. Теперь, поскольку f (r) должна быть плотностью вероятности, вы можете легко увидеть, что, интегрируя f (r) по интервалу (0, R), вы получите, что C = 2 / R ^ 2 (это упражнение для читателя .)

Таким образом, f (r) = 2 * r / R ^ 2

Хорошо, вот как вы получите формулу в ссылке.

Затем последняя часть идет от равномерной случайной величины u в (0,1), которую необходимо отобразить с помощью обратной функции кумулятивной функции распределения от этой требуемой плотности f (r). Чтобы понять, почему это так, вам нужно найти расширенный вероятностный текст, такой как, вероятно, папулис (или получить его самостоятельно).

Интегрируя f (r), вы получите F (r) = r ^ 2 / R ^ 2

Чтобы найти обратную функцию этого, вы устанавливаете u = r ^ 2 / R ^ 2, а затем решаете для r, что дает вам r = R * sqrt (u)

Это также имеет смысл интуитивно, u = 0 должно отображаться на r = 0. Кроме того, u = 1 должно отображаться на r = R. Кроме того, оно идет по функции квадратного корня, которая имеет смысл и соответствует ссылке.

Причина, по которой наивное решение не работает, заключается в том, что оно дает более высокую плотность вероятности точкам, расположенным ближе к центру круга. Другими словами, у круга, который имеет радиус r / 2, есть вероятность r / 2 получить выбранную точку, но у него есть область (количество точек) pi * r ^ 2/4.

Поэтому мы хотим, чтобы плотность вероятности радиуса имела следующее свойство:

Вероятность выбора радиуса, меньшего или равного данному r, должна быть пропорциональна площади круга с радиусом r. (потому что мы хотим иметь равномерное распределение по точкам, а большие области означают больше точек)

Другими словами, мы хотим, чтобы вероятность выбора радиуса между [0, r] была равна его доле от общей площади круга. Общая площадь круга равна pi * R ^ 2, а площадь круга с радиусом r равна pi * r ^ 2. Таким образом, мы хотели бы, чтобы вероятность выбора радиуса между [0, r] была (pi * r ^ 2) / (pi * R ^ 2) = r ^ 2 / R ^ 2.

Теперь приходит математика:

Вероятность выбора радиуса между [0, r] является интегралом p (r) dr от 0 до r (это просто потому, что мы добавляем все вероятности меньших радиусов). Таким образом, мы хотим, чтобы интеграл (p (r) dr) = r ^ 2 / R ^ 2. Мы можем ясно видеть, что R ^ 2 является константой, поэтому все, что нам нужно сделать, это выяснить, какой p (r) при интеграции даст нам что-то вроде r ^ 2. Ответ явно г * постоянный. интеграл (r * постоянная dr) = r ^ 2/2 * постоянная. Это должно быть равно r ^ 2 / R ^ 2, поэтому константа = 2 / R ^ 2. Таким образом, у вас есть распределение вероятности p (r) = r * 2 / R ^ 2

Примечание. Другой, более интуитивно понятный способ осмыслить проблему — представить, что вы пытаетесь присвоить каждому кругу радиус вероятности плотности ra, равный пропорции числа точек на его окружности. Таким образом, окружность с радиусом r будет иметь 2 * pi * r «точки» на своей окружности. Общее количество баллов: pi * R ^ 2. Таким образом, вы должны дать окружности ra вероятность, равную (2 * pi * r) / (pi * R ^ 2) = 2 * r / R ^ 2. Это намного проще для понимания и более интуитивно понятно, но не совсем математически обоснованно.

Пусть ρ (радиус) и φ (азимут) — две случайные величины, соответствующие полярным координатам произвольной точки внутри окружности. Если точки распределены равномерно, то какова функция распределения ρ и φ?

Для любого r: 0 2

Где S1 и S0 — площади круга радиуса r и R соответственно. Таким образом, CDF может быть дан как:

Обратите внимание, что для R = 1 случайная величина sqrt (X), где X равномерно на [0, 1), имеет этот точный CDF (потому что P [sqrt (X) — англичанин, иммигрировавшие в Австралии
источник

Это действительно зависит от того, что вы подразумеваете под «равномерно случайным». Это тонкий момент, и вы можете узнать больше об этом на странице вики здесь: http://en.wikipedia.org/wiki/Bertrand_paradox_%28probability%29 , где та же проблема, давая различные интерпретации для «равномерно случайных» дает разные ответы!

В зависимости от того, как вы выбираете точки, распределение может варьироваться, даже если они в некоторых смысле .

Кажется, что запись в блоге пытается сделать ее равномерно случайной в следующем смысле: если вы возьмете под круг окружности с тем же центром, то вероятность того, что точка попадет в эту область, пропорциональна площади область. Я полагаю, что это попытка следовать принятой в настоящее время стандартной интерпретации «равномерно случайных» для 2D-областей с определенными на них областями : вероятность падения точки в любом регионе (с четко определенной областью) пропорциональна площади этого региона.