Конспект
Рассмотрим окружность с центром в точке О и прямую a, её не пересекающую.
Расстояние от центра окружности до прямой равно длине перпендикуляра ОВ.
Это расстояние больше радиуса окружности.
Будем перемещать прямую, параллельно самой себе в сторону центра окружности. В определённый момент, прямая коснется окружности.
Расстояние от центра окружности до прямой равно радиусу окружности.
Прямая, имеющая с окружностью только одну общую точку называется касательной к окружности.
Общая точка прямой и окружности называется точкой касания.
Будем передвигать прямую далее к центру. Прямая пересечет окружность в двух точках.
Расстояние от центра окружности до прямой меньше радиуса.
Продолжая движение дальше, мы получим еще одну касательную к окружности.
Продолжим движение прямой дальше, она опять не будет иметь с окружностью общих точек.
Расстояние от центра окружности опять больше её радиуса.
Рассмотрим случай, когда прямая имеет с окружностью одну общую точку.
Сформулируем свойство касательной.
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Дано: Окружность с центром О, a – касательная, B – точка касания.
Доказать: a ⊥ OB
Доказательство:
Пусть утверждение неверно, т.е. прямая a не перпендикулярна радиусу OB. Тогда OB – наклонная к прямой a. Перпендикуляр меньше наклонной, тогда расстояние от центра O до прямой a меньше радиуса. Следовательно, прямая a и окружность имеют 2 общие точки. Но это противоречит условию, т.к. прямая a – касательная. Значит наше предположение неверно и a ⊥ OB.
Верно и обратное утверждение:
Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Проведем к окружности две касательные из одной точки, не принадлежащей окружности.
Выполняется утверждение:
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Докажите его самостоятельно, используя равенство треугольников AOВ и AOС.
Дано: окружность с центром O, касательные AB и AC
Доказать: AB = AC, ∠OAB = ∠OAC
Геометрия, 7-9: учеб. для общеобразоват. учреждений/ [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. – М.: Просвещение, 2017.
Видео:Определение кратчайшей расстоянии от точки до плоскостиСкачать

Расстояние от центра окружности до хорды
Рассмотрим, как найти расстояние от центра окружности до хорды.
Расстояние от точки до прямой измеряется длиной перпендикуляра, опущенного из этой точки на данную прямую. Значит, расстояние от центра окружности до хорды равно длине перпендикуляра, проведённого из центра окружности к этой хорде.
Например, расстояние от точки O — центра окружности — до хорды AB равно длине перпендикуляра OF:
Отрезки AB и CD являются хордами окружности. Найти расстояние от центра окружности до хорды CD, если AB=24, CD=10, а расстояние от центра окружности до хорды AB равно 5.


2) Треугольники AOB и COD — равнобедренные с основаниями AB и CD (AO=BO=CO=DO как радиусы).
Значит, их высоты OF и OK являются также медианами. Следовательно,
3) Рассмотрим треугольник AOF, где ∠AFO=90 º.
4) Рассмотрим треугольник COK, где ∠CKO=90 º.
Видео:Расстояние от точки до плоскости / Вывод формулыСкачать

Как найти расстояние между прямой и окружностью
Видео:10 класс, 19 урок, Расстояние от точки до плоскостиСкачать

Расстояние между двумя фигурами
Общее определение расстояния между двумя произвольными фигурами выходит за рамки школьной программы, и мы его не приводим. Ряд частных случаев, когда расстояние между двумя фигурами можно ввести на базе школьного материала, перечислен в следующей таблице.
| Фигуры | Рисунок | Определение расстояния |
| Две точки | 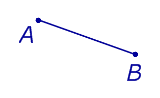 | Расстоянием между двумя точками называют длину отрезка AB. |
| Точка, лежащая на прямой | 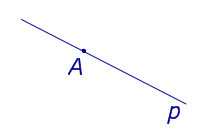 | Расстояние равно 0. |
| Точка, не лежащая на прямой | 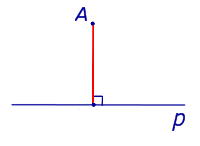 | Расстоянием от точки до прямой называют длину перпендикуляра, опущенного из точки на прямую. |
| Две параллельные прямые | 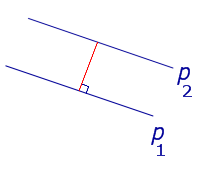 | Расстоянием между параллельными прямыми называют длину перпендикуляра, опущенного из любой точки одной прямой на другую прямую. |
| Две пересекающиеся прямые |  | Расстояние равно 0. |
| Две скрещивающиеся прямые | 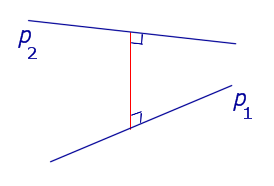 | Расстоянием между скрещивающимися прямыми называют длину общего перпендикуляра к этим прямым. |
| Точка, лежащая на плоскости |  | Расстояние равно 0. |
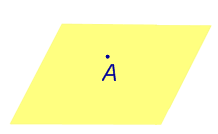
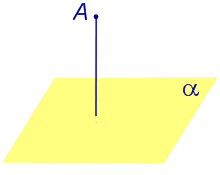
| Точка, не лежащая на плоскости | 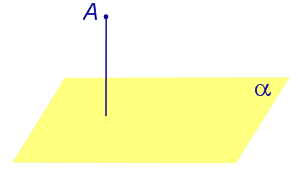 | Расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из этой точки на плоскость. |
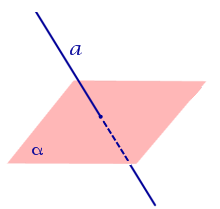
| Прямая, пересекающая плоскость | 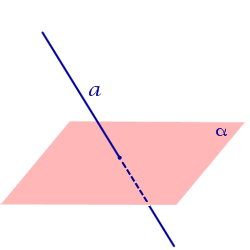 | Расстояние равно 0. |
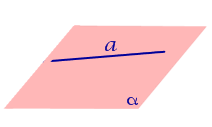
| Прямая, лежащая на плоскости |  | Расстояние равно 0. |
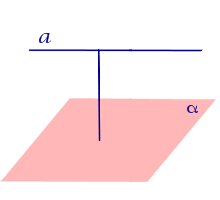
| Прямая, параллельная плоскости | 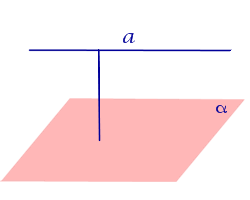 | Расстоянием от прямой, параллельной плоскости, до плоскости называют длину перпендикуляра, опущенного из любой точки данной прямой на плоскость. |
| Две пересекающиеся плоскости |  | Расстояние равно 0. |
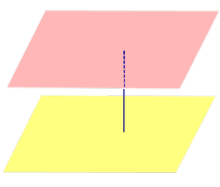
| Две параллельные плоскости | 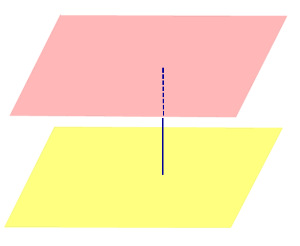 | Расстоянием между параллельными плоскостями называют длину перпендикуляра, опущенного из любой точки одной плоскости на другую плоскость (все такие перпендикуляры имеют одну и ту же длину). |
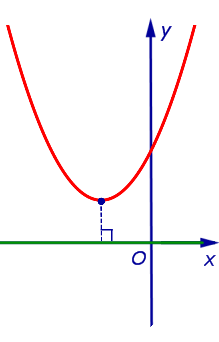
| Парабола y = a x 2 + b x + c , не пересекающая ось абсцисс, и ось абсцисс | 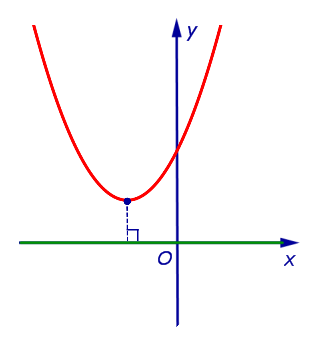 | Расстоянием от параболы, не пересекающей ось абсцисс, до оси абсцисс называют длину кратчайшего отрезка, один из концов которого лежит на параболе, а другой на оси абсцисс. Этим кратчайшим отрезком является перпендикуляр, опущенный из вершины параболы на ось абсцисс. |
| Окружность и не пересекающая ее прямая | 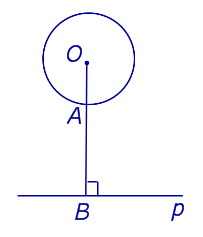 | Расстоянием между окружностью и непереcекающей ее прямой называют длину кратчайшего отрезка, один из концов которого лежит на окружности, а другой конец – на прямой. Если перпендикуляр OB , опущенный из центра O окружности на прямую, пересекает окружность в точке A, то расстояние от окружности до прямой равно длине отрезка AB. |
| Две непересекающиеся окружности, каждая из которых лежит вне другой | 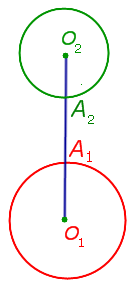 | Расстоянием между непересекающимися окружностями называют длину кратчайшего отрезка, один из концов которого лежит на одной окружности , а другой конец – на другой окружности. Если линия центров O1O2 пересекает окружность с центром O1 в точке A1, а окружность с центром O2 – в точке A2, то расстояние между окружностями будет равно длине отрезка A1A2. |
Гипербола 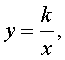 где k – любое, отличное от нуля, число, и ось абсцисс. где k – любое, отличное от нуля, число, и ось абсцисс. | 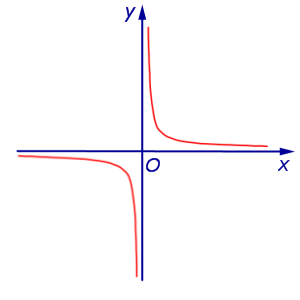 | Расстояние между гиперболой и осью абсцисс считается равным 0, поскольку гипербола неограниченно приближается к оси абсцисс (длина отрезка, один из концов которого лежит на гиперболе, а другой конец – на оси абсцисс, может быть сколь угодно малой). |
| Две точки |
 |
Определение расстояния:
Расстоянием между двумя точками называют длину отрезка AB.

Расстояние равно 0.

Определение расстояния:
Расстоянием от точки до прямой называют длину перпендикуляра, опущенного из точки на прямую.

Определение расстояния:
Расстоянием между параллельными прямыми называют длину перпендикуляра, опущенного из любой точки одной прямой на другую прямую.

Расстояние равно 0.
Определение расстояния:
Расстоянием между скрещивающимися прямыми называют длину общего перпендикуляра к этим прямым.
Расстояние равно 0.
Определение расстояния:
Расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из этой точки на плоскость.
Расстояние равно 0.
Расстояние равно 0.
Определение расстояния:
Расстоянием от прямой, параллельной плоскости, до плоскости называют длину перпендикуляра, опущенного из любой точки данной прямой на плоскость.
Расстояние равно 0.
Определение расстояния:
Расстоянием между параллельными плоскостями называют длину перпендикуляра, опущенного из любой точки одной плоскости на другую плоскость (все такие перпендикуляры имеют одну и ту же длину).
Определение расстояния:
Расстоянием от параболы, не пересекающей ось абсцисс, до оси абсцисс называют длину кратчайшего отрезка, один из концов которого лежит на параболе, а другой на оси абсцисс.
Этим кратчайшим отрезком является перпендикуляр, опущенный из вершины параболы на ось абсцисс.

Определение расстояния:
Расстоянием между окружностью и непереcекающей ее прямой называют длину кратчайшего отрезка, один из концов которого лежит на окружности , а другой конец – на прямой.
Если перпендикуляр OB , опущенный из центра O окружности на прямую, пересекает окружность в точке A , то расстояние от окружности до прямой равно длине отрезка AB.

Определение расстояния:
Расстоянием между непересекающимися окружностями называют длину кратчайшего отрезка, один из концов которого лежит на одной окружности, а другой конец – на другой окружности.
Если линия центров O1O2 пересекает окружность с центром O1 в точке A1, а окружность с центром O2 – в точке A2, то расстояние между окружностями будет равно длине отрезка A1A2.
Видео:Расстояние от точки до прямойСкачать

Взаимное расположение прямой и окружности
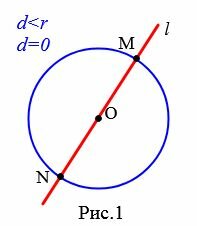
Выясним количество общих точек прямой и окружности в зависимости от их взаимного расположения. Если прямая l проходит через центр O окружности (Рис.1), то она пересекает окружность в двух точках, которые являются концами диаметра окружности.
Пусть прямая не проходит через центр окружности. Проведем перпендикуляр OH к прямой l (Рис.2, Рис.3, Рис.4). Обозначим расстояние от центра окружности до прямой l буквой d. Рассмотрим сколько общих точек будут иметь прямая и окружность в зависимости от соотношения d и r.
 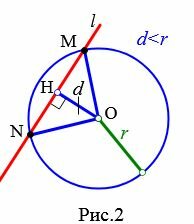 |
Теорема 1. Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.
В этом случае прямая называется секущей по отношению к окружности.
Доказательство. Пусть расстояние от центра окружности до прямой меньше радиуса окружности: d Теорема 2. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку.
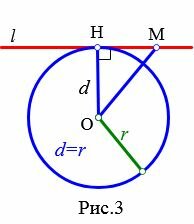 |
Доказательство. Пусть расстояние от центра окружности до прямой равно радиусу окружности: d=r (Рис.3). В этом случае OH=r, т.е. точка H лежит на окружности и является общей точкой прямой l и окружности. Возьмем на прямой l любую точку M отличной от H. Тогда расстояние от OM больше расстояния OH=r, поскольку наклонная OM больше перпендикуляра OH к прямой l. Следовательно точка M не лежит на окружности. Получили, что точка H единственная общая точка прямой l и окружности.
Теорема 3. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.
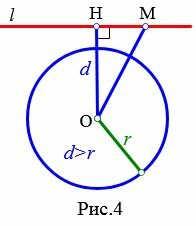 |
Доказательство. Пусть расстояние от центра окружности до прямой больше радиуса окружности:d>r (Рис.4). Тогда ( small OH > r). Возьмем на прямой l любую точку M отличной от H. Тогда ( small OM > OH>r). Следовательно точка M не лежит на окружности. Таким образом, если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.
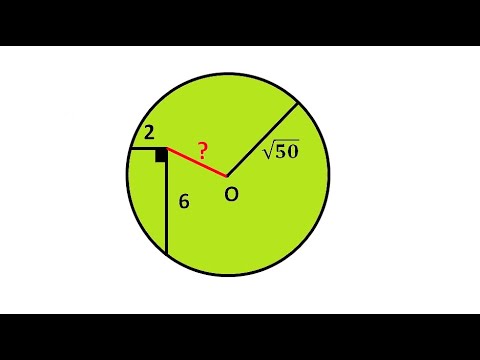
Видео:Найти расстояние от центра окружности до вершины прямого углаСкачать
61. Стереометрия  Читать 0 мин.
Читать 0 мин.
Видео:7 класс, 38 урок, Расстояние от точки до прямой. Расстояние между параллельными прямымиСкачать

61.333. Расстояния
Расстояния
Задача на нахождения расстояния в стереометрической фигуре является главной и самой важной из всех. Прежде всего определимся с тем, что имеется ввиду под словом «расстояние», ведь их может быть бесконечно много.
Расстояние между объектами в геометрии – это кратчайшее из расстояний между ними.
В стереометрии найти расстояние можно между следующими комбинациями фигур:
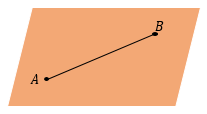
РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ
Расстояние между точками– это длина отрезка, соединяющего эти точки.
В задачах на стереометрию мы не можем просто воспользоваться линейкой, и длину этого отрезка должны найти аналитически. Поэтому длину отрезка AB между точками A и B находят как сторону треугольника, если отрезок AB удается включить в некоторый треугольник в качестве одной из его сторон.
То есть если в задаче предлагается найти расстояние между точками, нужно задать себе вопрос: «В каком треугольнике этот отрезок является стороной?», затем построить этот треугольник и найти в нем нужную сторону.
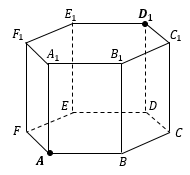
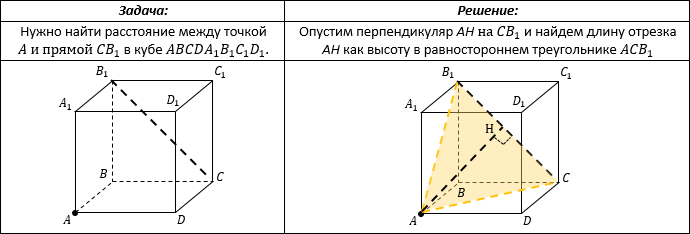
РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПРЯМОЙ
Расстояние от точки до прямой – длина перпендикуляра, опущенного из точки на прямую.
Этот отрезок перпендикуляра можно вычислить, включив его в треугольник (или трапецию) в качестве одной из высот. То есть нужно задать себе вопрос: «В каком треугольнике этот отрезок является высотой?», затем построить этот треугольник и найти в нем высоту.
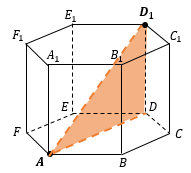
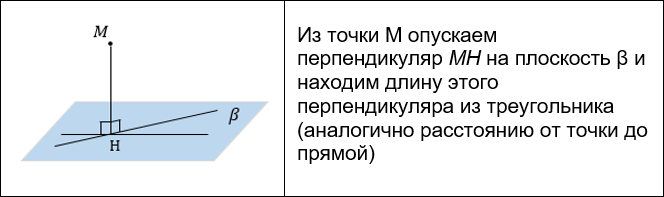
РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПЛОСКОСТЬЮ
Существует несколько способов нахождения расстояния от точки до плоскости:
- Построение перпендикуляра из точки на плоскость.
- К этому способу обращаются, если расстояние из точки M на плоскость опускать неудобно, а удобно опустить равный ему перпендикуляр из другой точки, лежащей на одной линии с M .
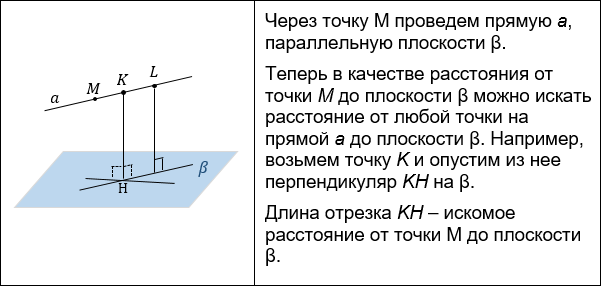
- Построение перпендикуляра из точки прямой к плоскости.
- Построение перпендикуляра из точки плоскости на плоскость.
К этому способу, аналогично, обращаются, если расстояние из точки M на плоскость опускать неудобно, а удобно опустить равный ему перпендикуляр из другой точки, лежащей на одной плоскости с M.
- Через двойное выражение объема.
Расстояние от точки M до плоскости β – это перпендикуляр, опущенный из точки на плоскость, то есть по сути это высота в некоторой пирамиде с вершиной M и плоскостью основания, лежащей на β. Если легко вычислить объем этой пирамиды, используя другое основание и другую высоту, то через этот объем можно найти нужное расстояние.
РАССТОЯНИЕ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ
Существует несколько способов нахождения расстояния между скрещивающимися прямыми:
1. Построение взаимного перпендикуляра.
2. Построение параллельной прямой.
К этому способу обращаются, если строить взаимный перпендикуляр неудобно и одна из скрещивающихся прямых уже заключена в удобную плоскость.
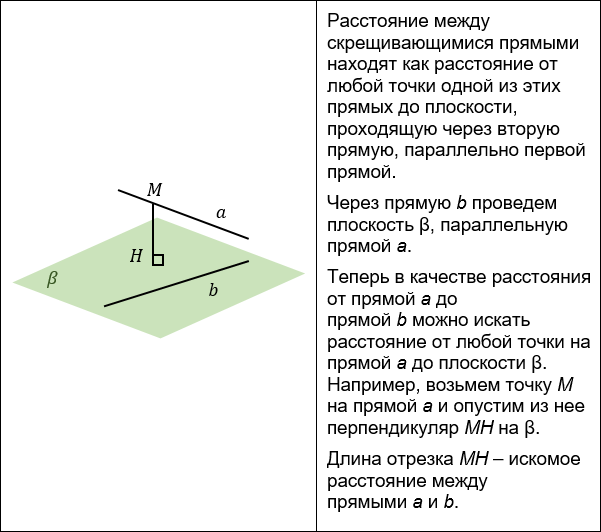
3. Построение параллельной плоскости.
🔍 Видео
18. Расстояние от точки до прямой в пространствеСкачать

Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать

19. Расстояние от точки до плоскостиСкачать

№631. Пусть d — расстояние от центра окружности радиуса r до прямой р. Каково взаимное расположениеСкачать

ВСЯ ГЕОМЕТРИЯ ЗА 10 МИНУТ / 7 КЛАСС / АТАНАСЯНСкачать

Расстояние между высотой и центром окружности (от точки до прямой) ОГЭ-ЕГЭСкачать

Как найти диаметр окружности, зная длину хорды и расстояние от центра окружности до неё? #огэ #егэСкачать

Когда ждать двойную индексацию пенсийСкачать

ПЛОЩАДЬ КОЛЬЦА. Сделай выбор: на чьей ты стороне?Скачать

Определение кратчайшей расстояние от точки до плоскости способом замены плоскостей проекцииСкачать

ЕГЭ Задание 16 Расстояние от точки до прямойСкачать

Лекция 24. Расстояние от точки до прямой на плоскости.Скачать

ЕГЭ по математике - Расстояние от точки до прямойСкачать

Расстояние точки до прямой, формула, которая обязательно поможет нам в параметрах😍😎 #математика #егэСкачать

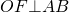
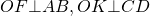
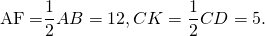
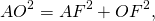
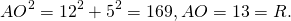


 Читать 0 мин.
Читать 0 мин.