На плоскости прямая и окружность могут либо пересекаться друг с другом, либо не пересекаться:
Расстояние от центра O до прямой m равно длине перпендикуляра OA. Следовательно, расстояние от центра окружности до прямой всегда будет равно перпендикуляру, опущенному из центра окружности на прямую.
Если расстояние от центра окружности до прямой больше радиуса данной окружности, то прямая и окружность не пересекаются и не имеют общих точек:
Видео:№631. Пусть d — расстояние от центра окружности радиуса r до прямой р. Каково взаимное расположениеСкачать

Касательная
Если расстояние от центра окружности до прямой равно радиусу данной окружности, то прямая касается окружности и они имеют одну общую точку, такая прямая называется касательной к окружности:
Прямая m — касательная. Точка соприкосновения прямой и окружности, то есть их общая точка, называется точкой касания: точка A — точка касания.
Касательная – это прямая линия, имеющая с окружностью одну общую точку.
Видео:Геометрия 8 класс (Урок№25 - Взаимное расположение прямой и окружности.)Скачать

Секущая
Если расстояние от центра окружности до прямой меньше радиуса данной окружности, то прямая пересекает окружность и они имеют две точки касания, такая прямая называется секущей к окружности:
Секущая – это прямая линия, имеющая с окружностью две общие точки.
Видео:№632. Расстояние от точки А до центра окружности меньше радиуса окружности. Докажите, что любаяСкачать

Взаимное расположение прямой и окружности
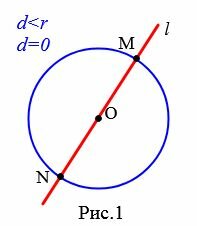
Выясним количество общих точек прямой и окружности в зависимости от их взаимного расположения. Если прямая l проходит через центр O окружности (Рис.1), то она пересекает окружность в двух точках, которые являются концами диаметра окружности.
Пусть прямая не проходит через центр окружности. Проведем перпендикуляр OH к прямой l (Рис.2, Рис.3, Рис.4). Обозначим расстояние от центра окружности до прямой l буквой d. Рассмотрим сколько общих точек будут иметь прямая и окружность в зависимости от соотношения d и r.
 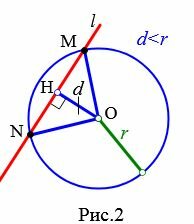 |
Теорема 1. Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.
В этом случае прямая называется секущей по отношению к окружности.
Доказательство. Пусть расстояние от центра окружности до прямой меньше радиуса окружности: d Теорема 2. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку.
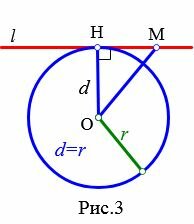 |
Доказательство. Пусть расстояние от центра окружности до прямой равно радиусу окружности: d=r (Рис.3). В этом случае OH=r, т.е. точка H лежит на окружности и является общей точкой прямой l и окружности. Возьмем на прямой l любую точку M отличной от H. Тогда расстояние от OM больше расстояния OH=r, поскольку наклонная OM больше перпендикуляра OH к прямой l. Следовательно точка M не лежит на окружности. Получили, что точка H единственная общая точка прямой l и окружности.
Теорема 3. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.
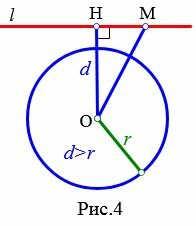 |
Доказательство. Пусть расстояние от центра окружности до прямой больше радиуса окружности:d>r (Рис.4). Тогда ( small OH > r). Возьмем на прямой l любую точку M отличной от H. Тогда ( small OM > OH>r). Следовательно точка M не лежит на окружности. Таким образом, если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.
Видео:8 класс, 31 урок, Взаимное расположение прямой и окружностиСкачать

Если расстояние от центра окружности до прямой больше радиуса окружности
Видео:ОГЭ ЗАДАНИЕ 16 НАЙДИТЕ ДЛИНУ ХОРДЫ ОКРУЖНОСТИ ЕСЛИ РАДИУС 13 РАССТОЯНИЕ ДО ХОРДЫ 5Скачать

Ваш ответ
Видео:Найти расстояние от центра окружности до вершины прямого углаСкачать
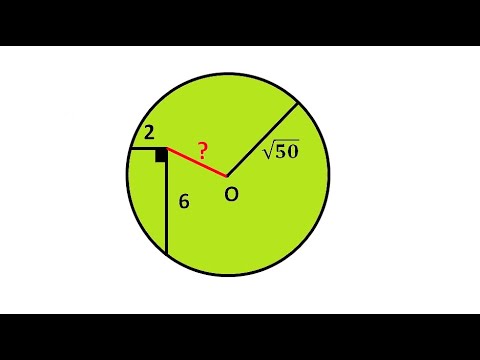
решение вопроса
Видео:Как найти диаметр окружности, зная длину хорды и расстояние от центра окружности до неё? #огэ #егэСкачать

Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,044
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
🔥 Видео
Планиметрия 12 | mathus.ru | расстояние между центрами пересекающихся окружностейСкачать

Прямая и окружность. Математика. 6 класс.Скачать

Расстояние между центрами вписанной и описанной окружностей треугольника и их радиусами #ShortsСкачать

Длина окружности. Математика 6 класс.Скачать

10 класс, 11 урок, Числовая окружностьСкачать

Найти центр и радиус окружностиСкачать

Радиус описанной окружностиСкачать

Геометрия на ЕГЭ. Расстояние от центра окружности до произвольной точки хорды. Степень точки.Скачать

Как найти центр и радиус нарисованной окружности #математика #егэ2023 #школа #fyp #shortsСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Найдите длину хорды окружности радиусом 13, если расстояние от центра окружности до хорды равно 5.Скачать

Окружность, диаметр, хорда геометрия 7 классСкачать

ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать





