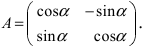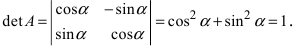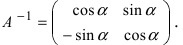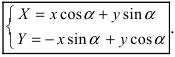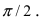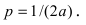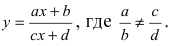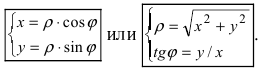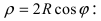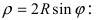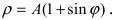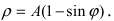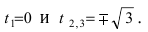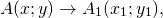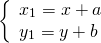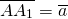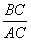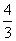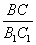- Окружность в параллельном переносе
- Преобразования декартовой системы координат с примерами решения
- Преобразования декартовой системы координат
- Параллельный перенос и поворот системы координат
- Полярные координаты. Замечательные кривые
- Параллельный перенос
- Метод параллельного переноса
- Параллельный перенос
- Геометрия. 9 класс
- Параллельный перенос, поворот плоскости и подобные треугольники
- Корзина
- Параллельный перенос
- Поворот плоскости вокруг точки на угол
- Подобные треугольники
- Параллельный перенос
- 📺 Видео
Видео:11 класс, 12 урок, Параллельный переносСкачать

Окружность в параллельном переносе
Видео:Геометрия 9 класс (Урок№29 - Параллельный перенос.)Скачать

Преобразования декартовой системы координат с примерами решения
Содержание:
Видео:9 класс, 32 урок, Параллельный переносСкачать

Преобразования декартовой системы координат
Параллельный перенос и поворот системы координат
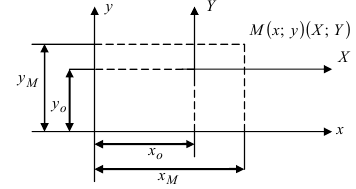
1. Параллельный перенос системы координат. Пусть на плоскости две декартовы системы координат, причем соответствующие оси параллельны и сонаправлены (Рис.46):
Рис. 46. Параллельный перенос одной системы координат относительно другой системы.
Систему координат
Пример:
Дана точка М(3;2) и начало новой системы координат 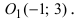
Решение:
Используя формулы, определяющие параллельный перенос одной системы отсчета относительно другой, получим 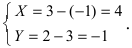
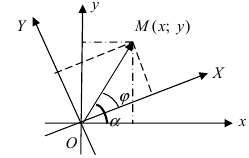
2. Поворот системы координат. Пусть даны две системы координат (старая и новая), имеющие общее начало отсчета и повернутые относительно друг друга на угол 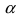
Рис. 47. Поворот одной системы координат относительно другой системы с общим началом координат двух систем.
Получим формулы, связывающие старые и новые координаты произвольной точки М(х; у). Из рисунка видно, что в новой системе координат координаты точки равны 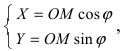
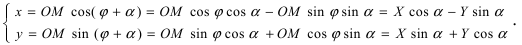
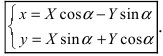
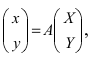
Найдем обратное преобразование системы координат, найдем матрицу 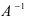
Найдем алгебраические дополнения всех элементов
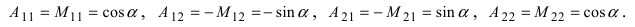
Определение: Унитарными преобразованиями называются такие преобразования, для которых определитель матрицы преобразования равен 1.
Определение: Ортогональными преобразованиями называются такие преобразования, для которых обратная матрица к матрице преобразования совпадает с транспонированной матрицей преобразования.
Таким образом, имеем 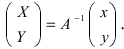
Пример:
Найти координаты точки М(1; 2) в новой системе координат, повернутой относительно старой системы отсчета на угол
Решение:
Воспользуемся полученными формулами 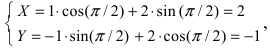
Рассмотрим применение преобразования координат:
а) Преобразовать уравнение параболы 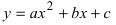
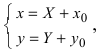
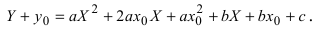
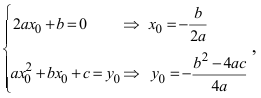
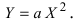
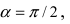
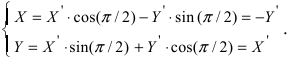
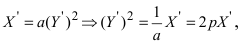
Пример:
Преобразовать уравнение параболы 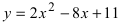
Решение:
Найдем начало отсчета новой системы координат после параллельного переноса 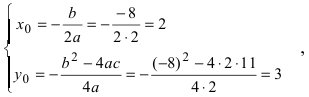
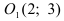
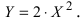
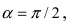
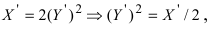
б) Выяснить, какую кривую описывает функция
Проведем следующее преобразование 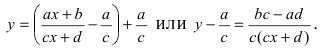
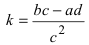
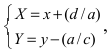
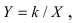
Полярные координаты. Замечательные кривые
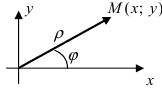
Пусть полярная ось совпадает с осью абсцисс Ох, а начало полярной оси (полюс полярной системы координат) совпадает с началом координат декартовой системы отсчета (Рис. 48). Любая точка М(х;у) в полярной системе координат характеризуется длиной радиус-вектора, соединяющего эту точку с началом отсчета и углом 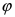
Рис. 48. Полярная система координат.
Главными значениями угла 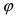
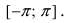
Рассмотрим замечательные кривые в полярной системе координат:
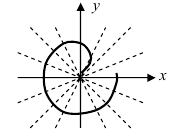
1. Спираль Архимеда 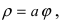
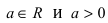
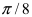
Рис. 49. Спираль (улитка) Архимеда.
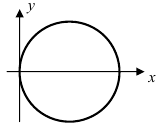
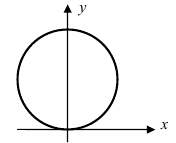
2. Уравнение окружности: уравнение 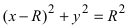
Рис. 50. Окружность с центром в точке A(R; 0) и радиусом R.
3. Уравнение 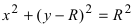
Рис. 51. Окружность с центром в точке А(0; R) и радиусом R.
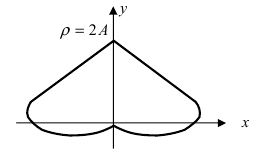
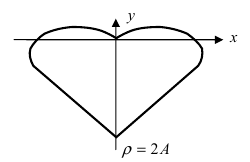
4. Кардиоиды:
Рис. 52. Кардиоида
Рис. 53. Кардиоида
Аналогично выглядят кардиоиды 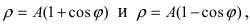
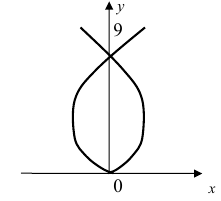
5. Петля: 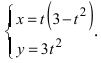
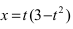
Для первого корня у = 0, а для второго и третьего — у = 9 . Следовательно, петля имеет вид
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
- Непрерывность функций и точки разрыва
- Точки разрыва и их классификация
- Экстремум функции
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Параллельный перенос. Симметрия. Поворот | МатематикаСкачать

Параллельный перенос
Параллельный перенос — это преобразование плоскости, при котором точки смещаются в одном и том же направлении на одно и то же расстояние.
Строгое определение параллельного переноса даётся либо через декартовы координаты, либо через вектор.
1) Введём на плоскости декартовы координаты x, y.
Параллельный перенос — это такое преобразование фигуры F, при котором её произвольная точка (x;y) переходит в точку (x+a; y+b), где a и b — некоторые числа, одинаковые для всех точек (x;y) фигуры F.
Формулы параллельного переноса

то параллельный перенос задаётся формулами:
Говорят также, что A1 является образом точки A при параллельном переносе на вектор (a; b). Точка A называется прообразом.
2) Параллельный перенос на данный вектор ā называется отображение плоскости на себя, при котором каждая точка A отображается в такую точку A1, то вектор AA1 равен вектору ā:
Свойства параллельного переноса
1) Параллельный перенос есть движение (то есть параллельный перенос сохраняет расстояние).
2) При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.
3) При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).
4) Каковы бы ни были точки A и A1, существует единственный параллельный перенос, при котором точка A переходит в точку A1.
В алгебре параллельный перенос широко используется для построения графиков функций.
Видео:Геометрия и группы. Алексей Савватеев. Лекция 2.3. Параллельный переносСкачать

Метод параллельного переноса
Перейдем сразу к решению задач на построение методом параллельного переноса.
Задача 6.34. Даны две окружности Fv F2 и прямая I. Провести прямую, параллельную прямой I, на которой окружности Fr и F2 высекают равные хорды.
Пусть прямая V искомая, т.е. прямая V высекает на данных окружностях равные хорды АВ иА’В’ (рис. 6.34).
Видео:Параллельный переносСкачать

Параллельный перенос
Параллельный перенос — это преобразование плоскости, при котором точки смещаются в одном и том же направлении на одно и то же расстояние.
Строгое определение параллельного переноса даётся либо через декартовы координаты, либо через вектор.
1) Введём на плоскости декартовы координаты x, y.
Параллельный перенос — это такое преобразование фигуры F, при котором её произвольная точка (x;y) переходит в точку (x+a; y+b), где a и b — некоторые числа, одинаковые для всех точек (x;y) фигуры F.
Формулы параллельного переноса

то параллельный перенос задаётся формулами:
Говорят также, что A1 является образом точки A при параллельном переносе на вектор (a; b). Точка A называется прообразом.
2) Параллельный перенос на данный вектор ā называется отображение плоскости на себя, при котором каждая точка A отображается в такую точку A1, то вектор AA1 равен вектору ā:
Свойства параллельного переноса
1) Параллельный перенос есть движение (то есть параллельный перенос сохраняет расстояние).
2) При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.
3) При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).
4) Каковы бы ни были точки A и A1, существует единственный параллельный перенос, при котором точка A переходит в точку A1.
В алгебре параллельный перенос широко используется для построения графиков функций.
Видео:Координаты вектора. 9 класс.Скачать

Геометрия. 9 класс
Конспект
Отметим точки A, B и зададим некоторый вектор а. Отложим вектор а от каждой из точек. При этом точка А отображается в точку А1, точка В отображается в точку В1. Таким образом вектор АА1 равен вектору ВВ1 и равны вектору а. Этот вид отображения плоскости на себя называется параллельным переносом.
Проведем отрезок АВ. Отложим вектор р от точек А и В. При этом точка А отображается в точку А1, точка В отображается в точку В1. Проведем отрезок А1В1. Отрезок АВ отображается на отрезок А1В1 при параллельном переносе на вектор р.
Построим треугольник ABC и задаем некоторый вектор а. Отложим вектор р от каждой из точек А, В, С. При этом точка А отображается в точку А1, точка В отображается в точку В1, точка С отображается в точку С1. Таким образом векторы АА1 = ВВ1 = СС1 и равны вектору а. Соединим отрезками точки А1, В1, С1. Треугольник АВС отображается на треугольник А1В1С1 при параллельном переносе на вектор а.
Сформулируем определение. Параллельным переносом на вектор р называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М1, что вектор ММ1 = р. Является ли параллельный перенос движением – отображением плоскости на себя, сохраняющим расстояние?
Пусть при параллельном переносе на вектор а точки M и N отображаются в точки M1 и N1. Так как вектор MM1 равен вектору a и вектор NN1 равен вектору a, то векторы MM1 и NN1 равны, т.е. MM1 = NN1, MM1 ║ NN1 следовательно, четырехугольник – параллелограмм, т.е. MN = M1N1. Значит, расстояние не изменяется. Таким образом доказали, что параллельный перенос является движением. Отметим следующие свойства.
При параллельном переносе:
1) отрезок переходит в равный ему отрезок;
2) угол переходит в равный ему угол;
3) окружность переходит в равную ей окружность;
4) любой многоугольник переходит в равный ему многоугольник;
5) параллельные прямые переходят в параллельные прямые;
6) перпендикулярные прямые переходят в перпендикулярные прямые.
Чтобы задать параллельный перенос достаточно задать некоторый вектор т.е. указать направление и расстояние.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Параллельный перенос, поворот плоскости и подобные треугольники
Корзина

Теоретический урок по предмету математики для решения задач по теме «Параллельный перенос, поворот плоскости и подобные треугольники».
Содержание данной онлайн страницы электронного справочника для школьников:
- – тема «Параллельный перенос» представлена на примере решения задач 145 — 148;
- – в контрольных работах с номерами 149 — 154 данной рабочей тетради по математике рассматривается поворот плоскости вокруг точки на угол;
- – повторение курса геометрии 9 класса в решениях приведено на примере заданий 155 — 173: углы треугольника, площадь треугольника через катеты и гипотенузу, вычисление радиуса описанной окружности, стороны ромба, подобные треугольники.
Видео:Поворот и параллельный перенос координатных осей. ЭллипсСкачать
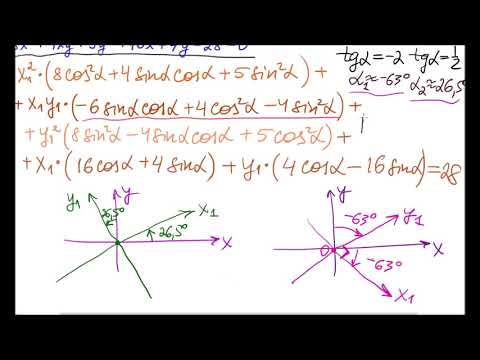
Параллельный перенос


Параллельным переносом на вектор 


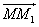

Задача 145.



A → A1 : 


B → B1 : 


Теорема:
При параллельном переносе на вектор 

f – параллельный перенос на вектор 
M 

N 



Точка M переводится движением в точку M1 с условием, что два вектора равны: M 



Точка N переводится движением в точку N1 с условием, что два вектора равны: N 



Следовательно, полученные отрезки параллельны MM1 || NN1 и построенные отрезки равны MM1 = NN1
Значит, четырехугольник MM1N1N – параллелограмм.
Поэтому MN = M1N1, значит f – движение.

Задача 146.
A 




B 




C 


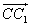


A 




B 




C 


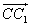



Задача 147.
точка D лежит на AC: D 
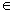
точка C лежит на AD: C 
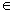
BC 
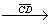
б) Доказать: ABB1D – равнобедренная трапеция
1) От точки B проведем прямую a, параллельную вектору 
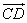

2) Точка B переводится движением в точку B1



3) Проведем прямую B1D, параллельную отрезку BC:
Рассмотрим четырехугольник BB1DC.
Т.к. основания BB1 || CD и боковые стороны BC || BD параллельны, то BB1DC – параллелограмм (по определению)
По свойству параллелограмма:
основания BB1 = CD и боковые стороны BC = BD равны, но AB = BC, тогда AB = B1D
Т.к. BB1 || AD параллельны и AB 
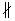
Т.к. AB = B1D, то ABB1D – равнобедренная трапеция.
Задача 148.
Дано: 
вектор 
окр (O;R) 

ΔABC 

EFPQ 

как показано на рисунке.
Видео:9 класс. Параллельный переносСкачать

Поворот плоскости вокруг точки на угол
Определение:




O – центр поворота
α – угол поворота
Задача 149.


α = 75° (против часовой стрелки)
O – центр поворота
1) A 
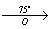


2) B 
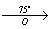


Теорема:
Поворот является движением.


α – угол поворота (против часовой стрелки)
точка O – центр поворота
Тогда треугольники равны ΔOMN = ΔOM1N1 по двум сторонам и углу между ними:




Тогда MN = M1N1, значит, f – движение.
Задача 150.
точка O – центр поворота


1) A 
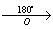


2) B 
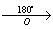


Задача 151.
точка A – центр поворота
α = 160° (против часовой стрелки)
1) B 
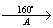


2) C 
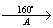


Задача 152.
точка O – центр поворота


1) A 
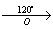


2) B 
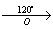


Задача 153.
точка C – центр окружности (C; R)
точка O – центр поворота
угол поворота α = 60° (против часовой стрелки)
а) точка C и точка O не совпадают
б) точка C и точка O совпадают


1) проведем луч CO
2) C 
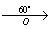



Т.к. точка О – центр поворота и точка С – центр окружности совпадают, то окружности (C;R) и (C1;R) будут тоже совпадать.

Задача 154.
Δ ABC – равнобедренный, равносторонний
D – точка пересечения биссектрис
D – центр поворота
угол поворота α = 120°
ΔABC 

Т.к. Δ ABC – правильный, то все углы в нем равны 60°.
Т.к. точка D – центр описанной и вписанной окружности, то
Δ ABD = Δ BDC = Δ DAC (по трем сторонам).
Следовательно, что 





A 

B 

C 

Таким образом, Δ ABC отображается на себя.
Повторение.
Задача 155.






Найти: наибольший угол треугольника
Пусть x – коэффициент пропорциональности. Зная, что сумма углов в треугольнике равна 180°, составим и решим уравнение:
3x + 7x + 8x = 180
Наибольший угол 

Задача 156.
треугольник ΔABC – равнобедренный,
один угол больше другого:






Найти: угол при основании треугольника
Пусть x° – угол при основании треугольника. Зная, что сумма углов в треугольнике составляет 180°, составим и решим уравнение:
(x + 60°) + x + x = 180°
Значит, 

Задача 157.
треугольник ΔABC – прямоугольный
c = 26 см – гипотенуза
Найти: больший катет b
Пусть x – коэффициент пропорциональности. По теореме Пифагора составим и решим уравнение:
(5x) 2 + (12x) 2 = 26 2
25x 2 + 144x 2 = 676
b = 12 • 2 = 24 (см)
Задача 158.


c = 13 – гипотенуза
По теореме Пифагора получаем:
a = 
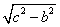

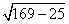

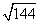
Тогда площадь треугольника
SΔABC = 


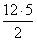
= 30 (квадратных единиц)
Задача 159.
треугольник ΔABC – равнобедренный,


c = 4 
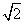
Найти: площадь треугольника SΔABC = ?
SΔABC = 

Т.к. Δ ABC – равнобедренный, то углы при основании по 45° и катеты равны a = b.
По теореме Пифагора получаем:
Тогда (4 
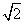
Тогда площадь треугольника
SΔABC = 


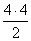
= 8 (квадратных единиц)
Задача 160.




Найти: радиус описанной окружности R = ?
Т.к. AH – медиана, то CH = 

По теореме Пифагора получаем:
Тогда CH = 


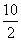
Точка H – центр описанной окружности
Т.к. R = AH, то R = AH = CH = 5 ед.
Задача 161.


соотношение острых углов




AC = 4 
Найти: радиус описанной окружности R = ?


Тогда 



Следовательно, BC = 

По теореме Пифагора получаем:
AC 2 + 
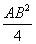
AC 2 = 

AB 2 = 
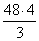
R = AD = BD = 8 : 2 = 4 (ед)
Задача 162.




радиус описанной окружности
Тогда AB = 2,5 • 2 = 5
По теореме Пифагора получаем:
AC = 
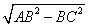

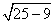

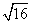




tg 


0,6 = 
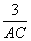

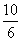
Задача 164.


Найти: 



Т.к. AH = AC, то Δ AHC – равнобедренный.
Точка H – радиус вписанной окружности, поэтому AH = CH, но AH = AC, следовательно, AH = CH = AC.
Тогда Δ AHC – равносторонний.
Значит, 





Задача 165.
треугольник Δ ABC – правильный, равносторонний,
SΔABC = 
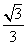
Найти: длину биссектрисы BH = ?


Рассмотрим Δ ABC – равнобедренный, где




Тогда BH – медиана, высота.
Значит, перпендикулярны отрезки BH 
Рассмотрим треугольники Δ ABH и Δ BHC.
AB = BC, по условию.
AH = CH, BH – медиана.
Значит, треугольники равны Δ ABH = Δ BHC.
Т.е. SΔABH = 




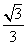

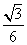
SΔABH = 

Рассмотрим треугольник Δ ABH.
Т.к. BH – биссектриса, то угол 

AH = 

SΔABH = 


AB • BH = 

По теореме Пифагора получаем:
AB 2 = AH 2 + BH 2
AB 2 = 

BH 2 = 

BH = 
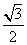
Используя результат (**) в уравнении (*), получаем
AB • 
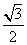

AB 2 = 
AB = 
Тогда AB • BH = 






Задача 166.
треугольник Δ ABC – правильный, равносторонний,


R = 
Найти: площадь треугольника
Рассмотрим Δ ABO (AO = BO = R) 

Проведем из вершины O к AB высоту OH.
Рассмотрим Δ AOH, где 

Т.к. 







OH = 


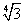

По теореме Пифагора получаем:
OH 2 + AH 2 = OA 2

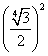

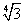



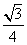
= 
AH 2 = 
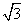

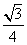

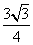



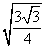

Тогда площадь треугольника
SΔAOH = 




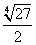

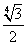

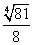

Следовательно, SΔABO = 2 • SΔAOH = 2 • 
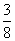


Тогда площадь треугольника
SΔABC = 3 • SΔABO = 3 • 


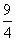




Площадь ромба SABCD = 384
Соотношение диагоналей ромба:
Найти: сторону ромба AB = ?
SABCD = 

Пусть x – коэффициент пропорциональности. Тогда
SABCD = 

Следовательно, диагональ BD = 4x = 4 • 8 = 32
AC = 3x = 3 • 8 = 24
Поэтому половина диагонали AO = 



BO = 



По теореме Пифагора получаем:
AO 2 + BO 2 = AB 2
Сторона ромба AB = 
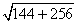

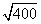
Задача 168.
треугольник Δ ABD – равнобедренный,


Найти: площадь треугольника
SΔABD = 

Проведем высоту BH к основанию AD.
По свойству равнобедренного треугольника:
BH – медиана, биссектриса, высота.
Т.к. BH – медиана, то AH = DH = 16 : 2 = 8 (ед.)
Рассмотрим треугольник Δ ABH, где угол 

По теореме Пифагора получаем:
AB 2 = AH 2 + BH 2
BH = 
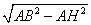

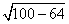

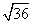
Тогда площадь треугольника
SΔABD = 



Ответ: площадь треугольника SΔABD = 48 кв.ед.

Задача 169.
треугольник Δ ABC –равнобедренный,
основание AC больше высоты BH на 15: AC > BH на 15
Найти: основание AC = ?
Т.к. треугольник Δ ABC –равнобедренный, то BH – высота, медиана, биссектриса.
Тогда AC = AH + CH = AH + AH = 2 AH
Рассмотрим Δ ABH – прямоугольный.
Пусть AC = (x) ед. 


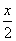
Тогда AB = (x – 15) ед. (по условию).
По теореме Пифагора решим уравнение:
(x – 15) 2 = ( 
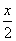



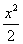
4 (x 2 – 30x) = x 2
4x 2 – 120x = x 2
3x 2 – 120x = 0 | : x
Таким образом, 40 ед. – длина основания.
Ответ: AC = 40 ед.
Видео:ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

Подобные треугольники
Задача 170.






CH – биссектриса угла 

Доказать: подобие треугольников
Δ BHC 









Т.к. CH – биссектриса угла 





Рассмотрим Δ BHC








Тогда 



Поэтому треугольники подобны Δ BHC 



верхнее основание BC = 4 см
нижнее основание AD = 10 см
диагональ BD = 8 см
часть диагонали BO = ?
соотношение периметров треугольников


Углы равны 



Углы равны 



Тогда треугольники подобны Δ BCO 




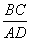

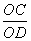







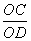













Пусть BO = x, AO = 8 – x. Тогда 10x = 4 • (8 – x)
x = 2 

Следовательно, BO = 2 



Ответ: BO = 2 



Задача 172.
ΔABC 



P (ΔABC) = 12 +16 + 20 = 48 (дм)
Т.к. треугольники подобны, то

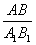

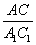




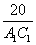


Тогда соотношение периметров треугольников

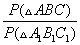
Из равенств (*) и (**) следует



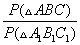




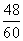

B1C1 = 
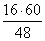
Тогда 





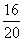



A1B1 = 
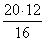
Задача 173.


стороны трапеции пересекаются в точке M:
Рассмотрим треугольники ΔAMD и ΔBMC:








Тогда, по первому признаку подобия треугольников:
треугольники подобны Δ AMD 


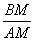

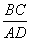

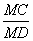


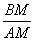

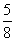
но AM = AB + BM = 3,9 + BM
8 • BM = 5 (3,9 + BM)

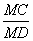

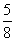
Видео:АвтоГраф. Векторы и параллельный переносСкачать

Параллельный перенос
Параллельный перенос — это преобразование плоскости, при котором точки смещаются в одном и том же направлении на одно и то же расстояние.
Строгое определение параллельного переноса даётся либо через декартовы координаты, либо через вектор.
1) Введём на плоскости декартовы координаты x, y.
Параллельный перенос — это такое преобразование фигуры F, при котором её произвольная точка (x;y) переходит в точку (x+a; y+b), где a и b — некоторые числа, одинаковые для всех точек (x;y) фигуры F.
Формулы параллельного переноса

то параллельный перенос задаётся формулами:
Говорят также, что A1 является образом точки A при параллельном переносе на вектор (a; b). Точка A называется прообразом.
2) Параллельный перенос на данный вектор ā называется отображение плоскости на себя, при котором каждая точка A отображается в такую точку A1, то вектор AA1 равен вектору ā:
Свойства параллельного переноса
1) Параллельный перенос есть движение (то есть параллельный перенос сохраняет расстояние).
2) При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.
3) При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).
4) Каковы бы ни были точки A и A1, существует единственный параллельный перенос, при котором точка A переходит в точку A1.
В алгебре параллельный перенос широко используется для построения графиков функций.
📺 Видео
Вычитание векторов. 9 класс.Скачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Смирнов С. В. - Дифференциальная геометрия - Параллельный перенос на поверхностиСкачать

Урок 8. Параллельный перенос. Декартовы координаты на плоскости.Скачать

Векторы. Метод координат. Вебинар | МатематикаСкачать

Видеоурок "Преобразование координат"Скачать

Параллельный перенос.Скачать

Понятие вектора. Коллинеарные вектора. 9 класс.Скачать