Все точки окружности находятся на одинаковом расстоянии от центра (3 видео)

Окружность. Круг.

Окружностью называется кривая замкнутая линия на плоскости, все точки которой находятся на одинаковом расстоянии от одной точки; эта точка называется центром окружности.

Часть плоскости, ограниченная окружностью, называется кругом.

Отрезок прямой, соединяющий точку окружности с её центром, называется радиусом (рис. 84).

Так как все точки окружности находятся от центра на одном и том же расстоянии, то все радиусы одной и той же окружности равны между собой. Радиус обыкновенно обозначается буквой R или r.

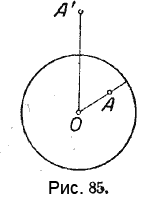
Точка, взятая внутри окружности, находится от её центра на расстоянии, меньшем радиуса. В этом легко убедиться, если через данную точку провести радиус (рис. 85).

Точка, взятая вне окружности, находится от её центра на расстоянии, большем радиуса. В этом легко убедиться, если соединить данную точку с центром окружности (рис. 85).

Отрезок прямой, соединяющий две точки окружности, называется хордой.

Хорда, проходящая через центр, называется диаметром (рис. 84). Диаметр обыкновенно обозначается буквой D. Диаметр равен двум радиусам:

Так как все радиусы одного и того же круга равны между собой, то и все диаметры данного круга равны между собой.

Теорема . Хорда, не проходящая через центр круга, меньше диаметра, проведённого в том же круге.

В самом деле, если проведём какую-нибудь хорду, например АВ, и соединим её концы с центром О (рис. 86), то увидим, что хорда АВ меньше ломаной линии АО + ОВ, т. е. АВ (breve); (breve) Задача. Через три точки, не лежащие на одной прямой, провести окружность.

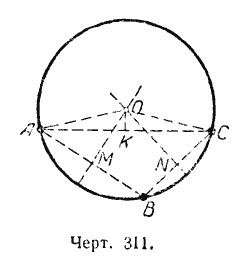
Пусть нам даны три точки А, В и С, не лежащие на одной прямой (черт.311).

Соединим эти точки отрезками АВ и ВС. Чтобы найти точки равноудалённые от точек А и В разделим отрезок АВ пополам и через середину (точку М) проведём прямую перпендикулярную к АВ. Каждая точка этого перпендикуляра одинаково удалена от точек А и В.

Чтобы найти точки, равноудалённые от точек В и С, разделим отрезок ВС пополам и через его середину (точку N) проведем прямую, перпендикулярную ВС. Каждая точка этого перпендикуляа одинаково удалена от точек В и С.

Точка О пересечения этих перпендикуляров будет находиться на одинаковом расстоянии от данных точек А, В и С (АО = ВО = СО). Если мы, приняв точку О за центр круга, радиусом, равным АО, проведём окружность, то она пройдёт через все данные точки А, В и С.

Точка О является единственной точкой, которая может служить центром окружности, проходящей через три точки А, В и С, не лежащие на одной прямой, так как два перпендикуляра к отрезкам АВ и ВС могут пересечься только в одной точке. Значит, задача имеет единственное решение.

Примечание. Если три точки А, В и С будут лежать на одной прямой, то задача не будет иметь решения, так как перпендикуляры к отрезкам АВ и ВС будут параллельны и не будет существовать точки, одинаково удаленной от точек А, В, С, т. е. точки, которая могла бы служить центром искомой окружности.

Если соединить отрезком точки А и С и середину этого отрезка (точку К) соединить с центром окружности О, то ОК будет перпендикулярна к АС (черт. 311), так как в равнобедренном треугольнике АОС ОК является медианой, поэтому ОК⊥АС.

Следствие. Три перпендикуляра к сторонам треугольника, проведённые через их середины пересекаются в одной точке.

Содержание

ГДЗ учебник по математике 5 класс Бунимович. Глава 1. Подведем итоги. Номер №4
Решение
Всё про окружность и круг
🌟 Видео

Видео:Как искать точки на тригонометрической окружности.Скачать

ГДЗ учебник по математике 5 класс Бунимович. Глава 1. Подведем итоги. Номер №4

Каким свойством обладают точки окружности? Что называют радиусом окружности? диаметром окружности?

Решение

Все точки окружности находятся на одинаковом расстоянии от центра.
Расстояние от центра до любой точки вне этой окружности больше радиуса.
Радиус − это отрезок соединяющий центр окружности с любой точкой, лежащей на этой окружности.
Диаметр − отрезок, соединяющий две точки окружности и проходящий через центр окружности.

Видео:Радиус и диаметрСкачать

Всё про окружность и круг

Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.

Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.

Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2

Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.

Квадрат касательной равен произведению секущей на ее внешнюю часть

Центральный угол — это угол, вершина которого совпадает с центром окружности.

Дугой называется часть окружности, заключенная между двумя точками.

Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.

Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.

Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.