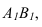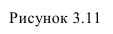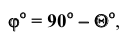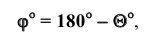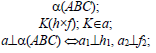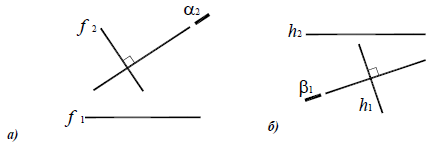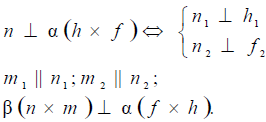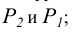Расстояние между параллельными прямыми способом замены плоскостей

Для решения целого ряда задач начертательной геометрии наиболее рациональным является метод замены плоскостей проекций. Например, с его помощью можно определить натуральную величину плоской фигуры, расстояние между параллельными прямыми, опорные точки пересечения поверхностей.

Видео:Определение расстояние между параллельными прямыми (Способ замены плоскостей проекции).Скачать

Замена одной плоскости проекции

Сущность метода заключается в замене одной из плоскостей проекций на дополнительную плоскость, выбранную так, чтобы в новой системе плоскостей решение поставленной задачи значительно упрощалось. Положение фигур в пространстве при этом не меняется.

Рассмотрим на примере точек A и B, как осуществляются построения на комплексном чертеже. Изначально точка A находится в системе плоскостей П₁, П₂. Введем дополнительную горизонтальную пл. П₄. Она будет перпендикулярна фронтальной плоскости проекций П₂ и пересечет её по оси x₁. Эту ось необходимо провести на комплексном чертеже с учётом цели построения. Здесь мы расположили её произвольно.

В новой системе плоскостей положение точки A» не изменится. Чтобы найти точку A’₁, которая является проекцией т. А на плоскость П₄, проведем из A» перпендикуляр к оси x₁. На этом перпендикуляре от точки его пересечения с осью x₁ отложим отрезок A_x1А’₁, равный отрезку A_xA’.

Данные построения основаны на равенстве ординат точек A’ и А’₁. Действительно, в системе плоскостей П₁, П₂ и в системе П₂, П₄ точка A удалена от фронтальной плоскости проекций П₂ на одно и то же расстояние.

Теперь осуществим перевод точки B в новую систему плоскостей П₁, П₄ (рис. ниже). Для этого введем произвольную фронтальную пл. П₄, которая будет перпендикулярна горизонтальной плоскости проекций П₁ и пересечет её по оси x₁.

В системе П₁, П₄ положение точки B’ останется неизменным. Чтобы найти точку B»₁, проведем из B’ перпендикуляр к оси x₁. На этом перпендикуляре от точки его пересечения с осью x₁ отложим отрезок B_x1B»₁ равный отрезку B_xB». Описанные построения основаны на равенстве аппликат точек B» и B»₁.

Видео:Метод замены плоскостей. Нахождение расстояния между прямыми общего положенияСкачать

Замена двух плоскостей проекций

Иногда для решения поставленной задачи требуется замена двух плоскостей проекций (рис. ниже). Пусть A’ и A» – исходные проекции точки A, находящейся в системе пл. П₁, П₂. Введем первую дополнительную плоскость П₄ и определим новую горизонтальную проекцию A’₁ точки A, как это было описано ранее.

Для осуществления второй замены плоскости проекций будем рассматривать систему пл. П₂, П₄ в качестве исходной. Введем новую фронтальную плоскость П₅ перпендикулярно горизонтальной пл. П₄. Для этого на произвольном месте чертежа проведем ось x₂ = П₄ ∩ П₅. Из точки A’₁, положение которой останется неизменным, восстановим перпендикуляр к оси x₂. На нем от точки A_x2 отложим отрезок A_x2A»₁ равный отрезку A»A_x1.

Видео:Определение кратчайшего расстояние между скрещивающимися прямыми методом замены плоскостей проекцииСкачать

Использование метода замены при решении задач

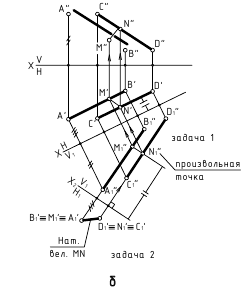
Владея методом замены применительно к одной точке, можно построить дополнительные проекции любых фигур, поскольку они представляют собой множество точек. На рисунке ниже показан перевод отрезка AB в частное положение. Новая плоскость П₄ проведена параллельно AB, поэтому отрезок проецируется на неё в натуральную величину.

На следующем рисунке показана плоскость общего положения α, заданная следами. Переведем её в новую систему плоскостей П₁, П₄ так, чтобы α занимала проецирующее положение. Для этого перпендикулярно горизонтальному следу h_0α введем дополнительную фронтальную плоскость П₄.

Новый фронтальный след f_0α1 строится по двум точкам. Одна из них, X_α1, лежит на пересечении h_0α с осью x₁. Дополнительно возьмем точку N, принадлежащую α, и укажем её фронтальную проекцию N»₁ на плоскости П₄.

Определение расстояния между параллельными плоскостями

Параллельные плоскости α и β расположены так, как показано на рисунке. Чтобы найти расстояние между ними, необходимо из произвольной точки A, взятой на пл. α, опустить перпендикуляр AB на пл. β и определить его настоящую длину.

Для уменьшения количества геометрических построений α и β предварительно переводятся в проецирующее положение с помощью метода замены плоскостей проекций. Вспомогательная точка M используется для определения направления следов f_0β1 и f_0α1, параллельных друг другу.

Видео:19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

Решение метрических задач в начертательной геометрии с примерами

Содержание:

К метрическим задачам относятся задачи на определение натуральной величины отрезков, расстояний углов, площадей плоских фигур.

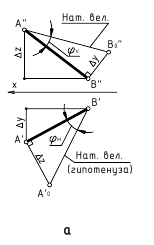
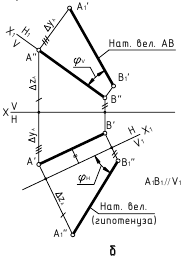
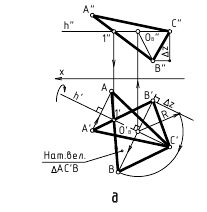
Определение натуральной величины отрезка и углов наклона к плоскостям проекций методом прямоугольною треугольника Натуральная величина отрезка равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция отрезка, а вторым — разность расстояний концов отрезка от той плоскости, на которой ведется построение. При этом угол между гипотенузой и катетом проекций является углом наклона отрезка к той плоскости, ряльной величины выполнено на горизонтальной проекции. Поэтому одним катетом прямоугольного треугольника, является горизонтальная проекция

Если необходимо определить угол наклона отрезка АВ к плоскости 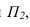то построение прямоугольного треугольника ведется на фронтальной проекции.

Видео:57. Определение расстояния между двумя параллельными прямымиСкачать

Решение метрических задач методами преобразовании проекций

Положении геометрических образов, при которых расстоянии и углы не искажаются на плоскостях проекций

Метрические характеристики объектов на чертежах не искажаются, если геометрические образы занимают частное положение относительно плоскостей проекций.

Приведем некоторые из них.

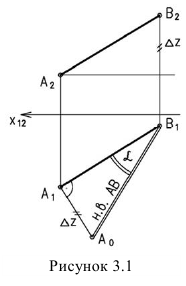
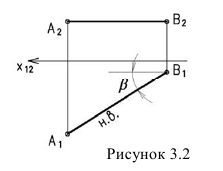
1. Прямая проецируется в натуральную величину, если она параллельна плоскости проекций (рисунок 3.2).

— угол наклона к плоскости

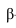
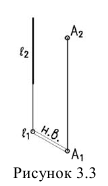
2. Расстояние от точки до прямой проецируется в натуральную величину, если прямая проецирующая (рисунок 3.3).

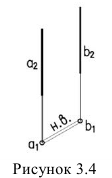
3. Расстояние между параллельными прямыми проецируется в натуральную величину, если прямые проецирующие (рисунок 3.4).

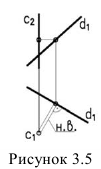
4. Расстояние между скрещивающимися прямыми проецируется в натуральную величину, если одна из прямых проецирующая (рисунок 3.5).

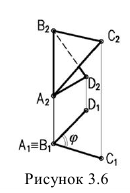
5. Угол между плоскостями (двугранный угол) проецируется в натуральную величину, если ребро угла проецирующее (рисунок 3.6).

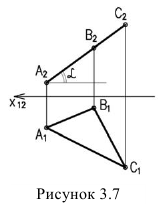
6. Угол наклона плоскости к плоскости проекций проецируется в натуральную величину, если плоскость проецирующая (рисунок 3.7)

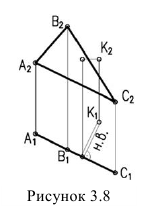
7. Расстояние от точки до плоскости проецируется в натуральную величину, если плоскость проецирующая (рисунок 3.8)

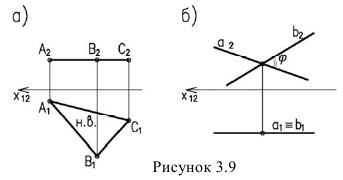
8. Любая плоская фигура проецируется в натуральную величину, если она параллельна плоскости проекций (рисунок 3.9а,б)

Таким образом, для решения метрических задач целесообразно данный объект привести в частное положение с тем, чтобы на одной из новых проекций получить более простое решение задачи.

Для такого перехода и служат способы преобразования проекций.

Существует несколько способов преобразовании проекций: способ вращения вокруг осей перпендикулярных плоскостям проекций, способ плоскопараллельного перемещения, способ замены плоскостей проекций и др.

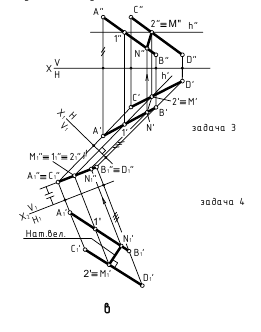
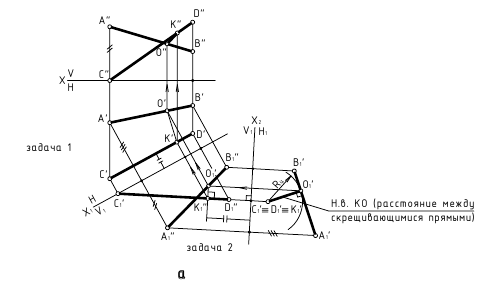
Четыре основных задачи преобразовании проекций

Этими способами решаются четыре основные задачи:

• Задача 1. Прямую общего положения преобразуем в линию уровня (одно преобразование).
• Задача 2. Прямую общего положения преобразуем в проецирующую (два преобразования)
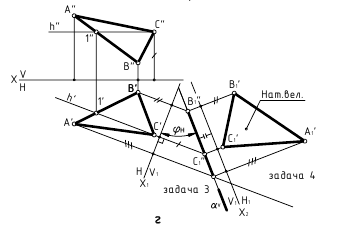
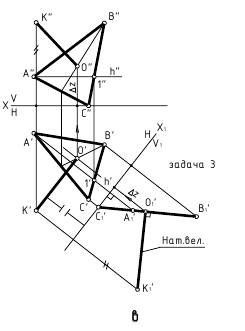
• Задача 3. Плоскость общего положения преобразуем в проецирующую (одно преобразование)
• Задача 4. Плоскость общего положения преобразуем в плоскость уровня (два преобразования)

Решение 1-ой и 2-ой задачи преобразовании проекций методом вращении, плоскопараллельного перемещении и замены плоскостей проекций

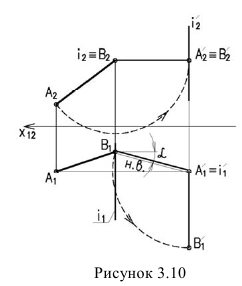
Способ вращения

Способ вращения заключается в том, что геометрические образы вращаются вокруг осей перпендикулярных плоскостям проекций до занятия ими какого-либо частного положения относительно плоскостей проекций. При этом одна проекция точки перемещается по окружности, вторая — но прямой параллельной оси проекций.

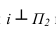
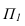
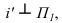
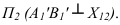
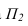
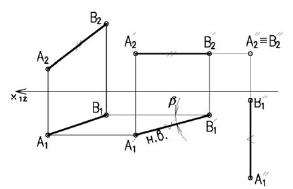
На рисунке 3.10 вокруг осивращаем отрезок ЛВ до положения параллельного плоскости(1 задача). Далее вращением вокруг осиполученный отрезок до положения перпендикулярного плоскости На отрезок с проецируется в точку

Способ плоскопараллельного перемещения

Способ плоскопараллельного перемещения является разновидностью способа вращения (вращение без закрепленных осей), т.е. положение объекта можно преобразовывать путем перемещения его параллельно одной плоскости проекций, одновременно изменяя его положение относительно другой плоскости проекций до занятия им какого-либо частного положения.

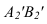
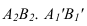
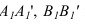
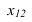
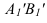
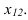
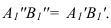
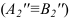
На рисунке 3.11 сначала АВ переводим из общего положения в положение горизонтальное. При этом должно быть равно по величина находим в пересечении вертикальных линий связи и линий параллельных оси (1 задача). Далее отрезок перемещаем до положения перпендикулярного оси При этом На фронтальной проекции отрезок с проецируется в точку (2 задача).

Способ замены плоскостей проекций

Сущность способа замены плоскостей проекций заключается в том, что старая система плоскостей проекций заменяется на новую, с таким расчетом, чтобы относительно новой системы плоскостей, геометрический образ занял какое-то частное положение. При этом нужно помнить, что линии связи будут перпендикулярны относительно новой оси проекций и расстояния от новой оси проекций до новой проекции точки равно расстоянию от старой проекции точки до старой оси.

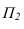
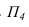
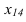
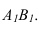
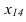
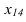
На рисунке 3.12 произведена первая замена плоскость заменена на новую фронтальную плоскость параллельную прямой АВ. При этом новая ось проводится параллельно проекции Линии связи проводятся перпендикулярно оси и на них от откладываются координаты z точек А и В (1 задача).

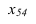
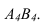
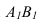
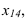
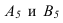
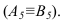
Далее прямую АВ преобразуем в проецирующую. Для этого проводим новую ось перпендикулярно проекции. Т.к. параллельна оси , расстояние до проекций будет одинаковое и прямая спроецируется в точку (2 задача)

Решение 3-ой и 4-ой задачи преобразовании проекций методом плоскопараллельного перемещения и замены плоскостей проекций

Так как метод вращения является более громоздким, рассмотрим решение 3-ей и 4-ой задачи преобразования методом плоскопараллельного перемещения и методом замены плоскостей проекций.

Способ плоскопараллельного перемещения

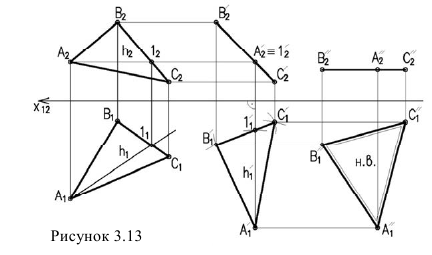
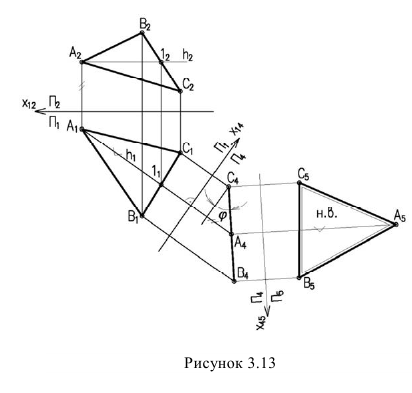
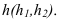
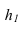
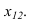
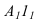
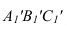
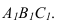
Для того чтобы плоскость из общего положения перевести в проецирующее, нужно иметь ввиду, что при этом ее горизонталь или фронталь должна быть перпендикулярна плоскости проекций. Поэтому на рисунке 3.13 проведена горизонталь Далее располагаем перпендикулярно оси Откладываем на ней отрезок и циркулем строим треугольник равный по величине На фронтальной проекции треугольник проецируется в линию (3 задача).

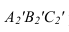
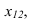
Чтобы плоскость треугольника перевести в положение плоскости уровня, достаточно полученную фронтальную проекцию расположить параллельно оси при этом на горизонтальной проекции треугольник проецируется в натуральную величину (4-я задача)

Способ замены плоскостей проекций

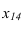
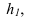
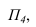
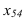
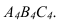
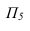
При решении задачи методом замены (рисунок 3.14) новую ось проводим перпендикулярно горизонтали тогда на новую фронтальную плоскость треугольник спроецируется в линию, т.е. станет перпендикулярным (3-я задача). Чтобы плоскость перевести в положение плоскости уровня, необходимо новую ось провести параллельно плоскости На новую плоскость треугольник спроецируется в натуральную величину.

Для того, чтобы методами преобразования решить любую метрическую задачу, необходимо определить какую из четырех основных задач преобразования необходимо решать в каждом конкретном случае.

Видео:Расстояние между скрещивающимися прямыми. Способ перемены плоскостей проекцийСкачать

Метрические задачи

Метрические задачи — это задачи на определение линейных или угловых размеров геометрических объектов, а также расстояний и углов между ними.

Главным вопросом метрических задач является вопрос о построении перпендикуляра к прямой или плоскости. Построение взаимно перпендикулярных прямых было рассмотрено ранее.

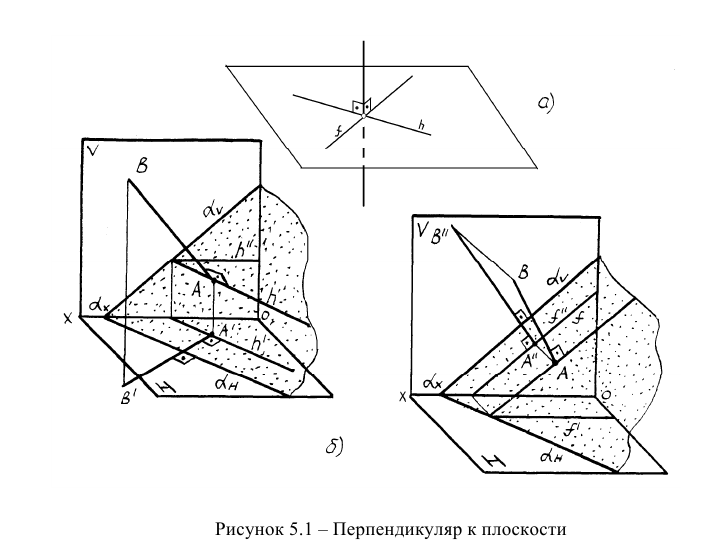
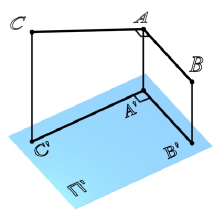
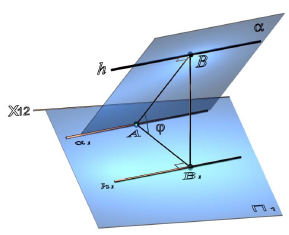
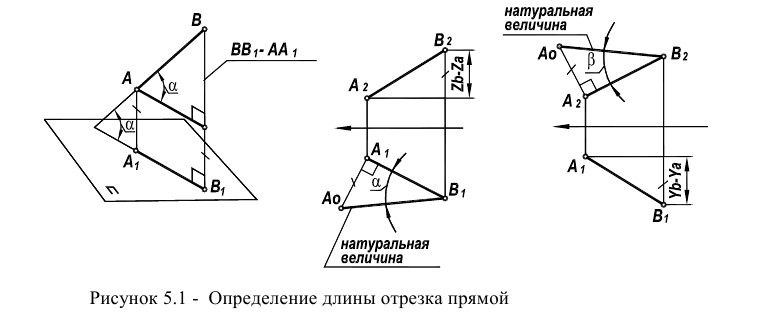
Из элементарной геометрии известно, что прямая перпендикулярна к плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости. В качестве этих пересекающихся прямых наиболее целесообразно использовать горизонталь и фронталь плоскости. Это объясняется тем, что только в этом случае прямой угол будет проецироваться в натуральную величину на соответствующие плоскости проекций. На рисунке 5.1 приведен пространственный чертеж, на котором из плоскости а (из точки А) восстановлен перпендикуляр АВ. Из приведенного изображения можно выяснить методику построения проекций перпендикуляра к плоскости: горизонтальная проекция перпендикуляра к плоскости проводится перпендикулярно горизонтальной проекции горизонтали или горизонтальному следу плоскости, а фронтальная проекция перпендикуляра проводится перпендикулярно фронтальной проекции фронтали или фронтальному следу плоскости. Таким образом, необходимо выполнить следующий алгоритм проведения проекций перпендикуляра к плоскости:

Построение перпендикуляра к плоскость и восстановление перпендикуляра из плоскости называется прямой задачей, а построение плоскости, перпендикулярной к прямой — обратной задачей. Обе задачи решаются по одному и тому же вышеописанному алгоритму. При этом плоскость, перпендикулярную заданной прямой, можно задать следами или пересекающимися горизонталью и фронталью.

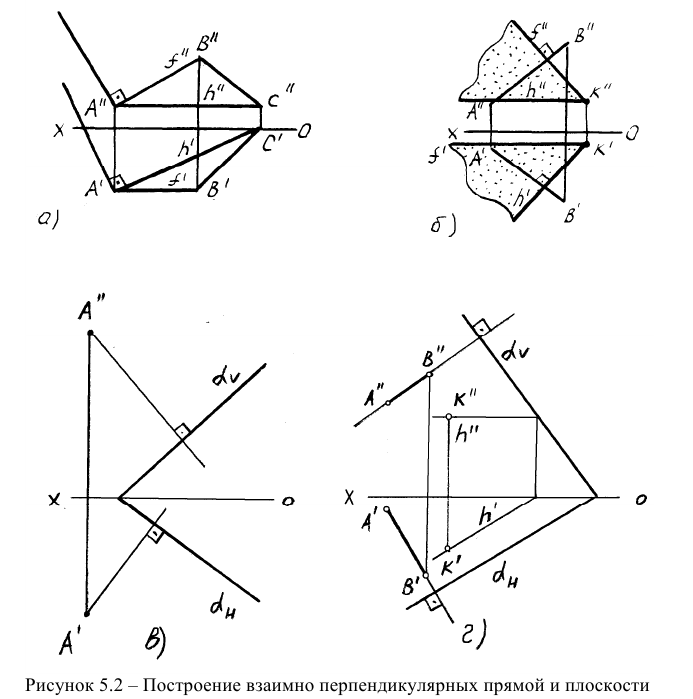
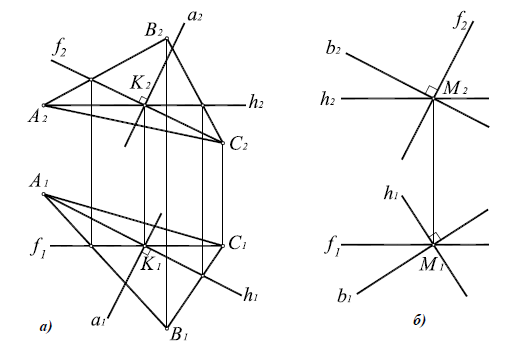
На рисунке 5.2 показано решение прямой (а) и обратной (б) задач. В прямой задаче из точки A треугольника AВС восстановлен перпендикуляр, в обратной задаче через точку К проведена плоскость, перпендикулярная прямой АВ. Плоскость задана пересекающимися горизонталью и фронталью.

Здесь же приведены примеры прямой и обратной задач, если плоскость задана следами. В прямой задаче (в) из точки Л построен перпендикуляр на плоскость, в обратной (г) — через точку К проведена плоскость перпендикулярно прямой АВ.

Определение расстояний между геометрическими объектами

Среди этих задач можно выделить следующие задачи: расстояние от точки до плоскости, расстояние от точки до прямой, расстояние между двумя параллельными прямыми, расстояние между двумя скрещивающимися прямыми, расстояние между двумя параллельными плоскостями и другие. В общем случае все задачи сводятся к определению расстояний между двумя точками.

Чтобы определить расстояние от точки до плоскости, необходимо выполнить ряд логических действий:

1. Из точки опустить перпендикуляр на заданную плоскость;
2. Найти точку встречи перпендикуляра с плоскостью;
3. Определить НВ расстояния между заданной и найденной точками.

Задача на определение расстояния от точки до прямой решается по следующему плану:

1. Через точку к провести плоскость, перпендикулярную заданной прямой;
2. Найти точку встречи М заданной прямой с проведенной плоскостью;
3. Соединить полученные точки (это будет перпендикуляр из точки на прямую);
4. Определить НВ перпендикуляра.

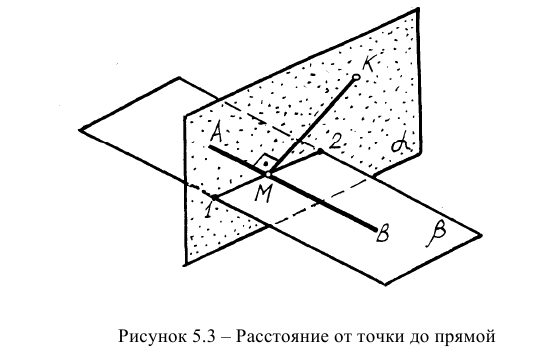
Пространственная модель решения второй задачи представлена на рисунке 5.3. Рассмотренная задача относится также к задачам на перпендикулярность двух прямых.

Другие упомянутые задачи на определение расстояний легче решаются методами преобразования эпюра, которые будут рассмотрены в последующих разделах.

Перпендикулярность плоскостей

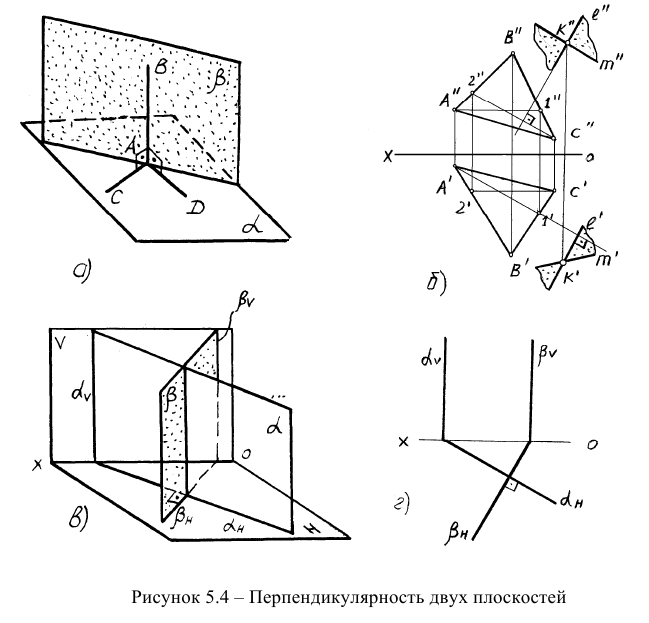
Плоскость перпендикулярна другой плоскости, если она содержит прямую, перпендикулярную другой плоскости (рисунок 5.4а). Таким образом, для того, чтобы провести плоскость, перпендикулярную другой, необходимо сначала провести перпендикуляр к заданной плоскости, а затем через него провести искомую плоскость. На рисунке 5.46 представлена задача: через точку К провести плоскость, перпендикулярную плоскости треугольника AВС. Искомая плоскость задана двумя пересекающимися прямыми, одна из которых перпендикулярна заданной плоскости.

Если две плоскости являются одноименными плоскостями частного положения (например, горизонтально- или фронтально-проецирующими), то при перпендикулярности плоскостей их собирательные следы будут перпендикулярны друг другу (рисунок 5.4в,г).

Если плоскости являются плоскостями общего положения, то при их перпендикулярности одноименные следы не будут взаимно перпендикулярны. Другими словами, перпендикулярность одноименных следов плоскостей общего положения не является достаточным условием для перпендикулярности самих плоскостей.

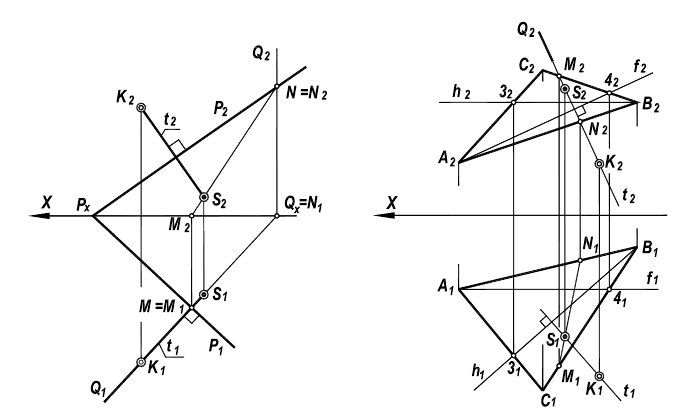
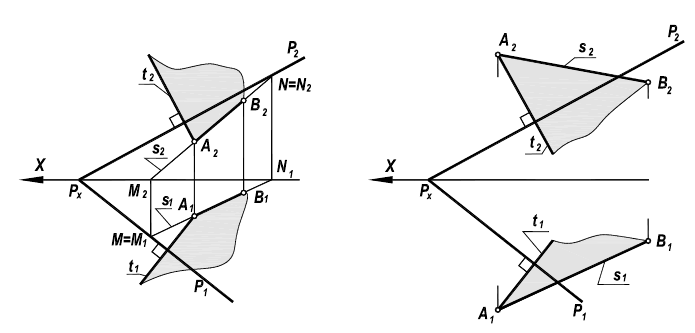
Определение углов между прямой и плоскостью и между двумя плоскостями

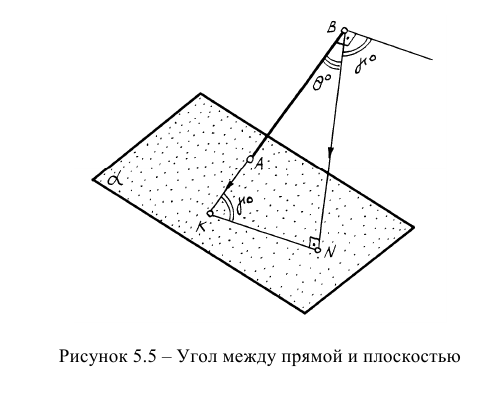
Определение углов между геометрическими объектами является трудоемкой задачей, если её решать традиционными геометрическими способами. Так, например, задачу на определение угла между прямой и плоскостью (рисунок 5.5) можно решить способом, алгоритм которого содержит следующие операции:

1. Определить точку встречи прямой АВ с плоскостью а;
2. Из точки В построить перпендикуляр на плоскость;
3. Найти точку встречи перпендикуляра с плоскостью;
4. Точки К и N соединить и определить НВ угла BKN.

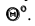
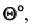
Однако задача может быть значительно упрощена, если использовать способ решения задачи с помощью дополнительного угла. Дополнительным углом назовем угол между заданной прямой АВ и перпендикуляром BN, обозначенный через Из приведенного рисунка видно, что, если из точки В прямой построить на плоскость перпендикуляр, определить НВ дополнительного угла то искомый угол определится по формуле:

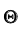
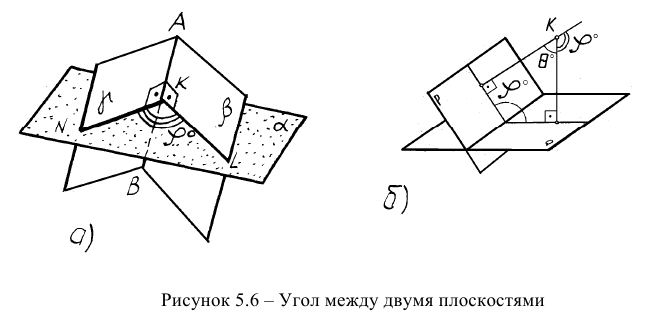
которую можно решить графически, достроив угол до 90°.

То же самое можно сказать о задаче на определение двугранного угла, то есть угла между двумя плоскостями (рисунок 5.66). Первый способ (геометрический) достаточно трудоемок. Он заключается в пересечении угла вспомогательной плоскостью а, перпендикулярной ребру АВ, построении линий пересечения KN и KL и определении натуральной величины угла NKL.

С помощью дополнительного угла задача решается следующим образом. В растворе двугранного угла (рисунок 5.6в) берут любую точку К и строят из неё перпендикуляры на обе плоскости двугранного угла, которые образуют дополнительный угол 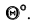Далее определяют НВ дополнительного угла и дополняют его (графически) до 180 градусов, исходя из формулы:

Дополненный угол будет искомым.

Натуральную величину дополнительного угла в обеих задачах наиболее целесообразно определять методом вращения вокруг горизонтали или фронтали, который будет изложен в последующих темах.

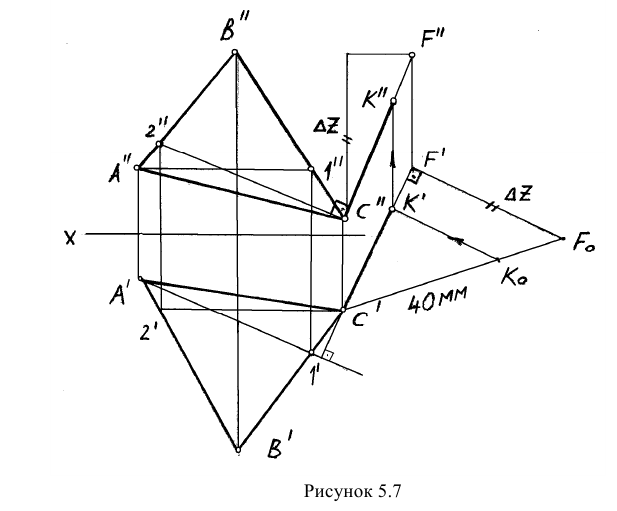
Пример: Из любой вершины треугольника АВС восстановить перпендикуляр длиной 40 мм.

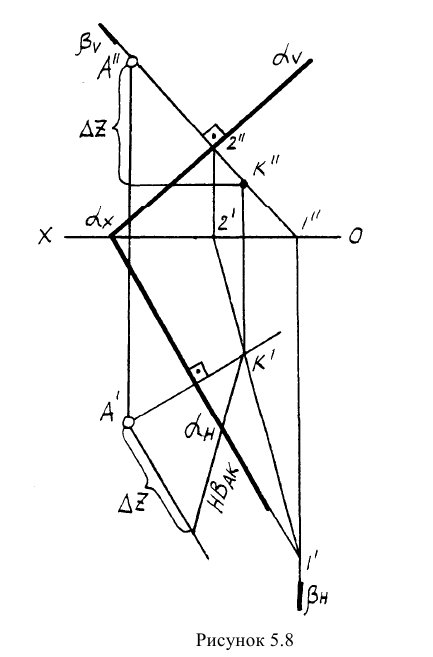
Решение: Сначала необходимо в плоскости треугольника АВС провести горизонталь и фронталь для того, чтобы построить проекции восстановленного перпендикуляра. Далее из точки С проводим проекции перпендикуляра согласно рассмотренному выше алгоритму о перпендикуляре к плоскости. Для того, чтобы отложить 40 мм, необходимо определить НВ ограниченного отрезка перпендикуляра CF (точку F берем произвольно). НВ отрезка CF определяем методом прямоугольного треугольника на горизонтальной проекции CF. Полученную точку К возвращаем на проекции по теореме Фалеса. Получаем проекции перпендикуляра длиной 40 мм (рисунок. 5.7).

Пример: Найти расстояние от точки А до плоскости, заданной следами

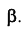
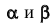
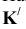
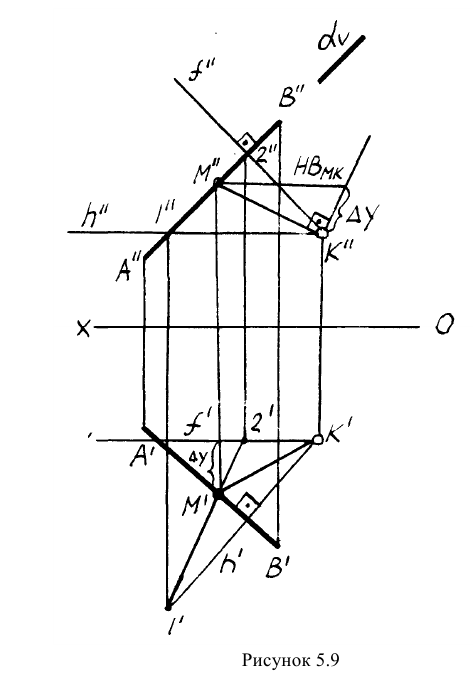
Решение: Из точки А строим перпендикуляр на заданную плоскость. Проекции перпендикуляра проводим перпендикулярно следам. Далее находим точку встречи перпендикуляра с заданной плоскостью с помощью вспомогательной фронтально-проецирующей плоскости Находим линию пересечения плоскостей (линия 1-2) и точку встречи в месте пересечения горизонтальной проекции перпендикуляра с линией 1-2. Методом прямоугольного треугольника определяем НВ расстояния АК (рисунок 5.8).

Пример: Определить расстояние от точки К до прямой AВ.

Решение: Через точку К проводим плоскость, перпендикулярную заданной прямой. Плоскость задаем пересекающимися горизонталью и фронталью. Их проекции проводим согласно алгоритму о перпендикуляре к плоскости (обратная задача). Далее находим точку встречи прямой AВ с проведенной плоскостью (точка М). Определяем натуральную величину КМ методом прямоугольного треугольника (рисунок 5.9).

Видео:Определение кратчайшей расстояние от точки до плоскости способом замены плоскостей проекцииСкачать

Примеры метрических задач

Задачи, в которых определяются различные геометрические величины -расстояния между объектами, длины отрезков, углы, площади и т.д. называются метрическими. Решение многих метрических задач, например задач на определение кратчайших расстояний, требует построения перпендикулярных прямых и плоскостей.

Перпендикулярность является частным случаем пересечения прямых, прямой и плоскости или двух плоскостей. Необходимо установить соотношения, по которым строятся проекции перпендикулярных прямых и плоскостей.

Теорема о проекциях прямого угла

Прямой угол проецируется на плоскость без искажения, если одна из его сторон параллельна этой плоскости (рис. 10.1).

Рис. 10.1. Теорема о проекциях прямого угла

Дано :BAC = 90°; AB || П’

Доказать, что C’A’A’B’

Доказательство: если AB||П’, то A’B’||AB, но AA’П’^AA’A’B’ значит ABAA,AB плоскости CAA’C’, тогда и A’B’ CAA’C’. Следовательно,CA’A’B’.

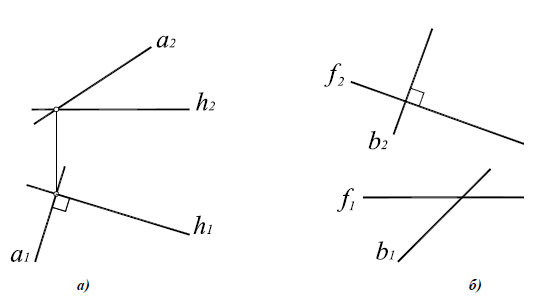
На основании этой теоремы две взаимно перпендикулярные прямые (пересекающиеся или скрещивающиеся) проецируются на П₁ в виде взаимно перпендикулярных прямых, если одна из них горизонталь, на П₂ — если одна из них фронталь (рис. 10.2,а).

Условие перпендикулярности скрещивающихся прямых (рис. 10.2,б) сводятся к условиям перпендикулярности пересекающихся прямых, поведенных через произвольную точку и соответственно параллельных скрещивающимся прямым. Таким образом, понятие перпендикулярности можно отнести как к пересекающимся, так и к скрещивающимся прямым.

Рис. 10.2. Перпендикулярные прямые:
а -пересекающиеся a₁ h₁ a h ;
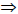
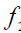
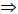
б -скрещивающиеся b2 ₂ b

Линии наибольшего наклона плоскости

Прямые, лежащие в плоскости и перпендикулярные линиям уровня этой плоскости, называются линиями наибольшего наклона к соответствующей плоскости проекций (рис. 10.3). Так, прямая, лежащая в плоскости и перпендикулярная горизонтали плоскости, называется линией наибольшего наклона к горизонтальной плоскости проекций, а прямая, перпендикулярная фронтали — линией наибольшего наклона к фронтальной плоскости проекций.

Угол между линией наибольшего наклона и ее проекцией на соответствующую плоскость равен углу наклона плоскости к плоскости проекций (см. рис. 9.15).

Рис. 10.3. Линия наибольшего наклона плоскости а к П₁:
а — плоскость общего положения; h ∈α — горизонталь плоскости а; AB h — линия наибольшего наклона;
φ = AB, AB ₁ — угол наклона плоскости а к П₁

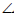
Перпендикулярность прямой и плоскости

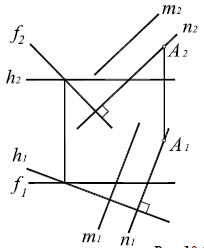
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости. На основании теоремы о проекциях прямого угла можно получить условие перпендикулярности прямой общего положения и плоскости общего положения:
Если прямая а перпендикулярна плоскости α(ABC), то ее горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция — фронтальной проекции фронтали плоскости.

Например, при построении прямой а, перпендикулярной плоскости α(ABC) (рис. 10.4,а), в плоскости строятся линии уровня — горизонталь и фронталь, затем через произвольную точку в плоскости, в данном случае точку K(h×), строится прямая, горизонтальная проекция которой перпендикулярна горизонтальной проекции горизонтали плоскости α(ABC), а фронтальная проекция — фронтальной проекции фронтали плоскости.

Рис. 10.4. Перпендикулярность прямой и плоскости:

а -построение прямой, перпендикулярной плоскости:

б -построение плоскости, перпендикулярной прямой:

Аналогично решается задача о построении плоскости, перпендикулярной прямой общего положения (рис. 10.4,б)

Если плоскость проецирующая, проекции линий уровня совпадают со следом плоскости, перпендикулярность устанавливается по отношению к следу плоскости. Горизонтальная проекция перпендикуляра к горизонтально-проецирующей плоскости строится перпендикулярно горизонтальному следу плоскости (рис. 10.5,а). Прямая, перпендикулярная горизонтально-проецирующей плоскости, занимает положение горизонтальной линии уровня.
Аналогично, фронтальная проекция перпендикуляра к фронтально-проецирующей плоскости строится перпендикулярно фронтальному следу плоскости (рис. 10.5,б). Прямая, перпендикулярная фронтально-проецирующей плоскости, занимает положение фронтали.

Рис. 10.5. Перпендикулярность прямой и проецирующей плоскости:
а -построение прямой, перпендикулярной плоскости;
б -построение плоскости, перпендикулярной прямой

Взаимная перпендикулярность плоскостей

Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Таким образом, построение взаимно перпендикулярных плоскостей сводится к построению перпендикулярных прямой и плоскости. Например, чтобы через произвольную точку А провести плоскость, перпендикулярную плоскости a(× h) (рис. 10.6), достаточно построить прямую n,перпендикулярную плоскости α(×h): n₁h₁; n₂₂. Вторая прямая m, определяющая искомую плоскость, может быть задана произвольно — как пересекающая прямую n или параллельная ей.

Рис. 10.6. Перпендикулярность двух плоскостей

Дано: α(h × ) ; A (A₁, A₂).

Построить: A ∈ β α .

Видео:Расстояние между параллельными прямымиСкачать

Определение метрических задач

Традиционно задачи, связанные с измерением длин, углов, площадей и объемов относят к метрическим. В основе решения этих задач лежит определение длины отрезка и, как производной от этого, площади плоской фигуры.

Определение длины отрезка

Одним из наиболее распространенных методов (рисунок 5.1) является метод прямоугольного треугольника (так его называют в начертательной геометрии) или метод ортогональных дополнений (название, принятое в линейной алгебре).

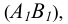
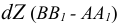
Идея метода базируется на следующем. Истинная величина отрезка AВ является гипотенузой прямоугольного треугольника, один из катетов которого, является проекцией отрезка AВ на плоскость проекции а второй катет -разница координат концов отрезка для оси, отсутствующей в рассматриваемой плоскости проекции (ортогональное дополнение). Угол между проекцией и гипотенузой этого треугольника (а) определяет наклон прямой к соответствующей плоскости проекции.

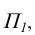
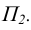
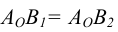
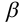
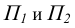
На комплексном чертеже возможно решение как на плоскости так и на плоскости При правильных построениях . Углы а и -углы наклона отрезка прямой АВ к плоскости соответственно.

Определение площади треугольника

Определение площади треугольника и величины плоского угла можно свести к известной задаче построения треугольника по трем сторонам.

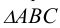
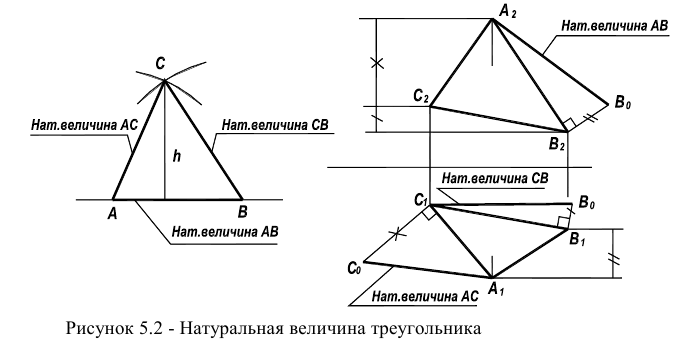
Для этого достаточно, используя рассмотренный выше способ прямоугольного треугольника, найти по порядку истинные величины сторон (в соответствии с рисунком 5.2), а затем на свободном месте построить треугольник по трем сторонам.

Величина плоского угла между двумя любыми сторонами этой фигуры может быть измерена на истинной величине треугольника.

Проецирование прямого угла

Решение многих задач Начертательной геометрии связано с необходимостью построения на чертеже взаимно перпендикулярных прямых и плоскостей. Базой для этого служит умение строить прямые углы на комплексном чертеже.

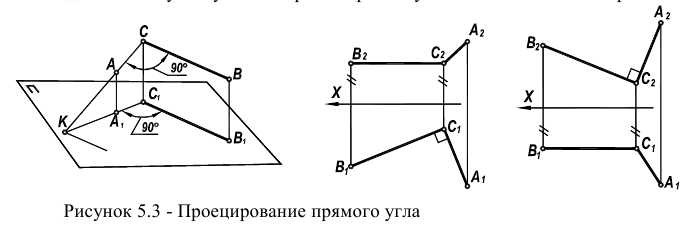
Известная в теории чертежа теорема (приведем ее без доказательства) утверждает, что прямой угол (в соответствии с рисунком 5.3) проецируется на

соответствующую плоскость проекций вез искажения, если одна из его сторон параллельна этой плоскости проекций, а вторая — ей не перпендикулярна.

Перпендикулярность прямых и плоскостей

Выше уже отмечалось, что в трехмерном Евклидовом пространстве отсутствует полная параллельность, то же самое можно сказать и о перпендикулярности. Понятие перпендикулярности так же, как и параллельности, вводится через определение.

Перпендикулярность прямой и плоскости

Считают, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся (любым) прямым этой плоскости.

При решении задачи возможны два варианта: проведение перпендикулярной прямой к плоскости из внешней точки и из точки, лежащей в плоскости.
Рассмотрим возможность проведения перпендикуляра из точки К, лежащей в плоскости общего положения Р, заданной следами (рисунок 5.4).

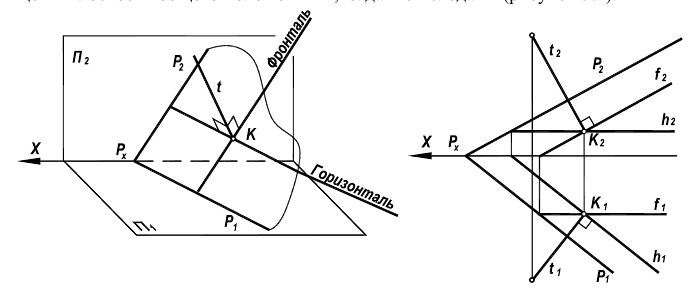
Рисунок 5.4 — Перпендикулярность прямой и плоскости

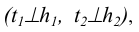
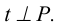
В плоскости Р (через точку К) проводятся горизонталь h и фронталь f. Прямые, перпендикулярные соответствующим проекциям линий уровня в соответствии с теоремой о проецировании прямого угла и данным выше определением, могут быть приняты за проекции прямой .

В том случае, когда точка К не лежит в плоскости Р, решение задачи аналогично (рисунок 5.5).

Поскольку положение точки пересечения искомого перпендикуляра не определено, решение соответствует следующей схеме:

а) в плоскости проводятся горизонталь h (через точку В) и фронталь f (через точку A), в случае задания плоскости следами за фронталь и горизонталь принимаются соответствующие следы плоскости

Рисунок 5.5 — Перпендикуляр к плоскости

б) из внешней точки К к соответствующим проекциям линий уровня (следам) проводятся перпендикулярные прямые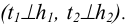— Линия t принимается за перпендикуляр, опущенный из точки К к плоскости Р;

в) определяется точка S пересечения этого перпендикуляра t и плоскости.

Расстояние от точки до плоскости

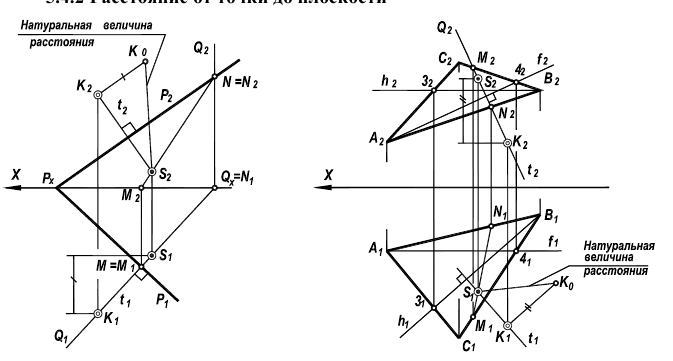
Рисунок 5.6 — Расстояние от точки до плоскости

Задачу на определение расстояние от точки до плоскости (рисунок 5.6) можно свести к решению уже известных задач на построение перпендикуляра к плоскости (рисунок 5.5) и определения натуральной величины отрезка прямой (рисунок 5.1)

Перпендикулярность плоскостей

Считают, что две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную другой плоскости.

Задача может ставиться, как проведение плоскости, перпендикулярной заданной, проходящей через точку или прямую.

При проведении искомой плоскости через точку, как и в предыдущем случае, возможны два варианта проведения плоскости перпендикулярной заданной: через точку, лежащую в плоскости и через точку вне ее (рисунок 5.7).

Точно такой же вариант возникает и при проведении перпендикулярной плоскости через прямую (лежащую в исходной плоскости или не лежащую).

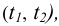
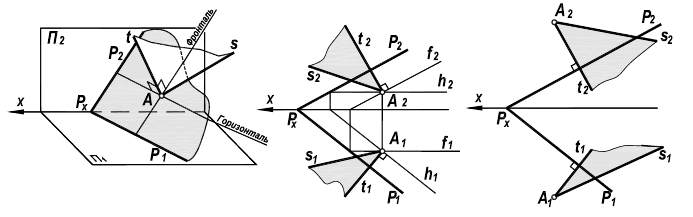
Рассмотрим вариант построения плоскости, проходящей через точку. Пусть точка А лежит в плоскости Р. Линии перпендикулярные соответствующим проекциям линий уровня (следам), определят перпендикуляр t к плоскости Р.

Рисунок 5.7 — Перпендикулярность плоскостей
Проведение через точку А произвольной прямой s позволяет определить плоскость Q, которая будет перпендикулярна плоскости Р.

Если точка А лежит вне плоскости Р, то решение аналогично. Проведение через точку А перпендикуляра t и произвольной прямой s определит плоскость Q, которая также, по определению, будет перпендикулярна плоскости Р.

Решение задачи на проведение плоскости через прямую аналогично решению задачи по проведению плоскости через точку. Достаточно вместо произвольной прямой s использовать заданную прямую АВ. И тогда, в соответствии с рисунком 5.8, задача сведется к проведению перпендикуляра t к плоскости Р (из точки, лежащей в плоскости или лежащей вне ее).

Рисунок 5.8 — Перпендикулярность плоскостей

Определение натуральных величин геометрических элементов

1. Определить натуральную величину отрезка общего положения:

• способом прямоугольного треугольника;
• способом замены плоскостей проекций преобразовать в прямую уровня;
• способом вращения вокруг проецирующей оси преобразовать в прямую уровня.

2. Определить натуральную величину плоскости общего положения (замкнутого отсека):

• способом замены плоскостей проекций преобразовать в плоскость уровня;
• способом вращения вокруг линии уровня преобразовать в плоскость уровня;
• способом плоскопараллельного перемещения преобразовать в плоскость уровня.

Определение расстояния между геометрическими элементами (образами)

1. Определить расстояние от точки до прямой общего положения:

• способом замены плоскостей проекций преобразовать плоскость, заданную прямой и точкой, в плоскость уровня (задачи 3 и 4 преобразования; прямую и точку рассматривать как плоскость);
• способом замены плоскостей проекций преобразовать прямую общего положения в проецирующую прямую (задачи 1 и 2 преобразования);
• способом вращения вокруг линии уровня преобразовать плоскость, заданную прямой и точкой, в плоскость уровня;
• способом плоскопараллельного перемещения преобразовать плоскость, заданную прямой и точкой, в плоскость уровня;
• способом задания плоскости, перпендикулярной к прямой (3-й тип задач), построить через заданную точку плоскость, перпендикулярную к прямой, и определить точку пересечения последней с плоскостью.

2. Определить расстояние между параллельными прямыми:

• способом замены плоскостей проекций преобразовать плоскость, заданную параллельными прямыми, в плоскость уровня (задачи 3 и 4 преобразования);
• способом замены плоскостей проекций преобразовать две параллельные общего положения в проецирующие прямые (задачи 1 и 2 преобразования);
• способом вращения вокруг линии уровня преобразовать плоскость, заданную параллельными прямыми, в плоскость уровня, ограничив ее замкнутым отсеком;
• способом плоскопараллельного перемещения преобразовать плоскость, заданную параллельными прямыми, в плоскость уровня;
• способом задания плоскости, перпендикулярной к прямой (3-й тип задач), построить плоскость через любую точку, принадлежащую одной из прямых, перпендикулярную ко второй прямой, и определить точку пересечения этой плоскости со второй прямой.

3. Определить расстояние между скрещивающимися прямыми, преобразовав одну из прямых в проецирующую (задачи 1 и 2 преобразования).

4. Определить расстояние от точки до плоскости:

• по теме «Перпендикулярность» – провести перпендикуляр к плоскости, построить точку пересечения этого перпендикуляра с заданной плоскостью и найти любым способом натуральную величину построенного отрезка (см. пункт 1);
• способом замены плоскостей проекций преобразовать плоскость общего положения в плоскость проецирующую.

5. Определить расстояние от точки до поверхности вращения:

• способом замены плоскостей проекций преобразовать плоскость, проведенную через точку и ось вращения поверхности, в плоскость уровня (задача 4 преобразования);
• способом вращения вокруг проецирующей оси повернуть плоскость, проведенную через точку и ось вращения поверхности, в плоскость уровня.

Определение углов наклона геометрических элементов к плоскостям проекций H и V

1. Определить углы наклона прямой общего положения к плоскостям проекций H и V:

• способом прямоугольного треугольника построить на двух проекциях натуральные величины отрезка и определить углы наклона прямой;
• способом замены плоскостей проекций преобразовать прямую общего положения в горизонтальную, а затем во фронтальную прямую (задача 1 преобразования);
• способом вращения вокруг соответствующей проецирующей оси преобразовать прямую общего положения в горизонтальную и во фронтальную прямые.

2. Определить угол наклона прямой к заданной плоскости общего положения:

• из любой точки прямой опустить перпендикуляр к плоскости;
• способом вращения вокруг линии уровня преобразовать построенную плоскость, заданную прямой и перпендикуляром, в плоскость уровня;
• искомый угол будет дополнять построенный угол до 90°.

3. Определить величину двухгранного угла, если на чертеже есть линии пересечения плоскостей, образующих двухгранный угол (ребро):

• способом замены плоскостей проекций преобразовать ребро двухгранного угла в проецирующую прямую (задачи 1 и 2 преобразования).

4. Определить угол между двумя плоскостями общего положения, если на чертеже нет линии пересечения заданных плоскостей (ребра):

• задача решается косвенным путем, для чего из любой точки пространства следует опустить перпендикуляры к заданным плоскостям, которые, в свою очередь, задают вспомогательную плоскость, перпендикулярную к этим плоскостям;
• эту вспомогательную плоскость способом вращения вокруг линии уровня следует преобразовать в плоскость уровня, определив угол между перпендикулярами (преобразование вспомогательной плоскости в плоскость уровня возможно и другими способами – ее плоскопараллельным перемещением или заменой плоскостей проекций);
• искомый угол будет дополнять построенный угол до 180° (углом между плоскостями считают угол острый).

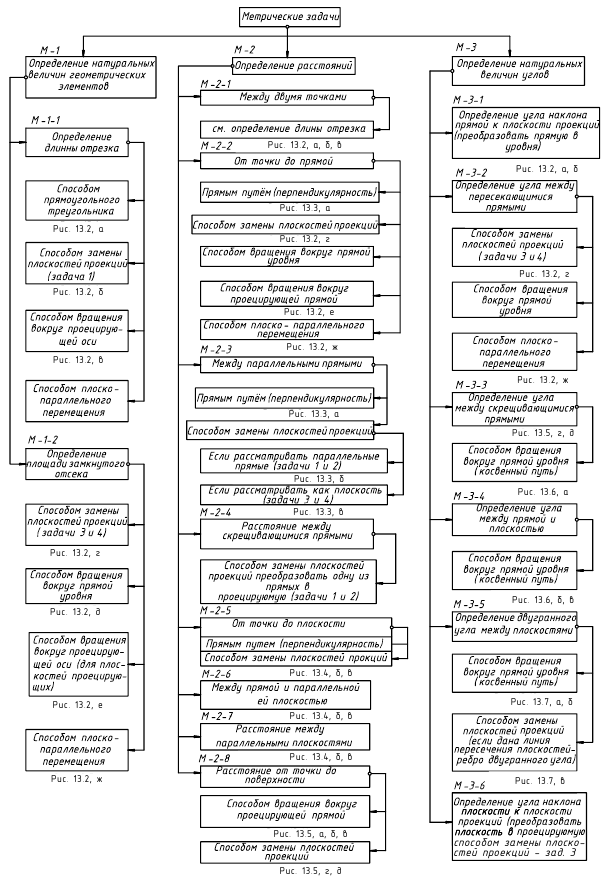
Структуризация материала тринадцатой лекции в рассмотренном объеме схематически представлена на рис. 13.1 (лист 1). На последующих листах 2–7 компактно приведены иллюстрации к этой схеме для визуального повторения изученного материала при его повторении (рис. 13.2–13.7).

Метрические задачи:

Определение натуральной величины геометрических элементов:

1. Определение длины отрезка

Способ прямоугольного треугольника

Способ замены плоскостей проекций (задача 1)

Способ вращения вокруг проецирующей оси

2. Определение площади замкнутого отсека

Способ замены плоскостей проекций (задачи 3 и 4)

Способ вращения вокруг прямой уровня (горизонтали)

Способ вращения вокруг проецирующей оси i(i V)

Способ плоско-параллельного перемещения (переноса)

Определение расстояний:

1. Расстояние между точками — определяется величиной отрезка, соединяющего эти точки

2. Расстояние от точки до прямой — определяется величиной перпендикуляра, опущенного из точки к прямой

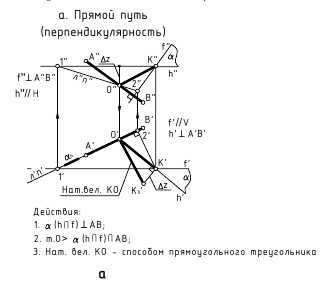
а. Прямой путь (перпендикулярность)

б. Способ замены плоскостей проекций: определить натуральную величину плоскости, которую определяют точка и прямая (см.рис. 13.2, г)

в. Способ вращения вокруг прямой уровня: определить натуральную величину плоскости, которую определяют точка и прямая (см.рис.13.2, д)

г. Способ плоскопараллельного переноса: определить натуральную величину плоскости, которую определяют точка и прямая (см.рис.13.2, ж)

3. Расстояние между параллельными прямыми — определяется величиной перпендикуляра, проведённого из произвольной точки одной прямой к другой прямой

а. Способ замены плоскостей проекции (рассматриваем две прямые) — задачи 1 и 2 (преобразовать прямые общего положения AB и CD в проецирующие)

б. Способ замены плоскостей проекции (рассматриваем плоскость, которую определяют параллельные прямые) — задачи 3 и 4 (определить натуральную величину плоскости ? (AB//СВ))

4. Расстояние между скрещивающимися прямыми — определяется величиной перпендикуляра, проведённого от одной из прямых, преобразованной в точку, к другой прямой (задачи 1 и 2 замены плоскостей проекции).

Способ замены плоскостей проекций — задачи 1 и 2

5. Расстояние от точки до плоскости — определяется величиной перпендикуляра, проведённого из точки на плоскость до точки его пересечения с этой плоскостью.

а. Прямой путь (перпендикулярность)

б. Способ замены плоскостей проекций (плоскость преобразовать в проецирующую — задача 3)

6. Расстояние между прямой и параллельной ей плоскостью — определяется величиной перпендикуляра, проведённого из произвольной точки на прямой к плоскости.

7. Расстояние между параллельными плоскостями — определяется величиной отрезка перпендикуляра, опущенного из точки одной плоскости на другую плоскость (до точки пересечения с другой плоскостью).

8. Расстояние от точки до поверхности

a. Cпособ вращения вокруг проецирующей оси

б. Способ замены плоскостей проекции

Определение величин углов:

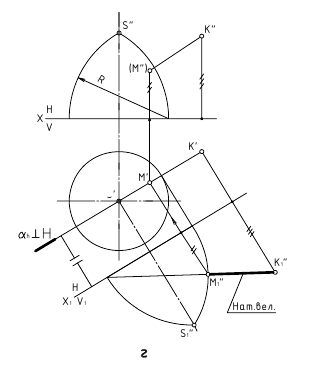
1. Угол φ между скрещивающимися прямыми — определяется плоским углом, образованным двумя пересекающимися прямыми, проведёнными из произвольной точки пространства параллельно скрещивающимся прямым (рис. 13.6, а)

Способ вращения вокруг линии уровня

Дано:
а и b — скрещивающиеся прямые
Требуется:
∠φ — ?

Решение:
1.
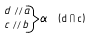
2. ∠φ — вращением вокруг фронтали, проведённой в построенной плоскости α(d ∩с)

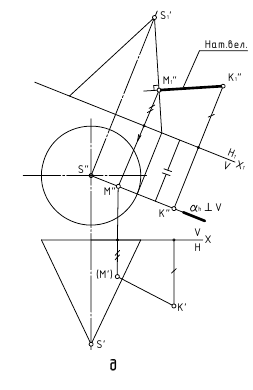
2. Угол φ между прямой и плоскостью — определяется углом между прямой и её проекцией на эту плоскость.

Дано:
α(h ∩ f);
AB — прямая общего положения
Требуется:
∠φ — ?

Решение:
1. l α(h ∩ f);
l» f»;
l‘ h’;
2. ∠φ — вращением вокруг фронтали, проведённой в построенной плоскости β(AB∩l)

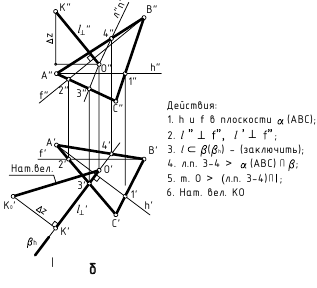
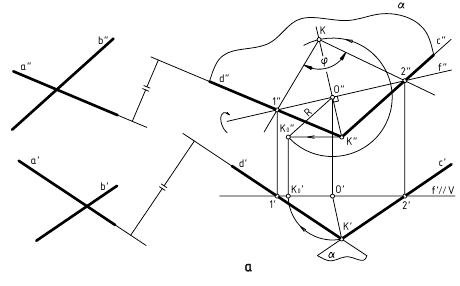
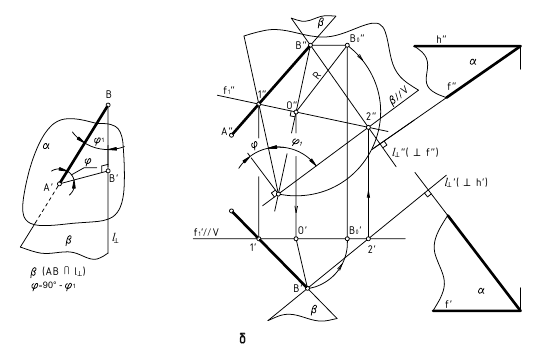
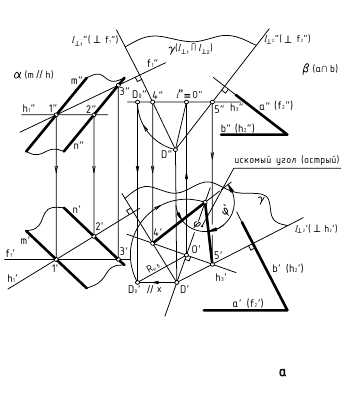
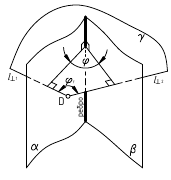
3. Угол φ между плоскостями α и β — определяется линейным углом, образованным двумя прямыми, по которым некоторая плоскость γ, перпендикулярная плоскостям (или их ребру), пересекает эти плоскости (углом между плоскостями считают острый угол).

а. Если на чертеже нет ребра (линии пересечения заданных плоскостей) — угол φ определяется способом вращения вокруг линии уровня (рис. а)

Дано:
(m // h); (а ∩ b).
Требуется:
∠φ — ?
Решение:
1. провести в заданной плоскости фронтали и горизонтали;

2. из произвольной точки пространства D (D’, D») провести перпендикуляры l₁ и l₂ к заданными плоскостям, которые определяют плоскость γ(l₁ ∩ l₂);
3. ∠φ — вращением вокруг горизонтали h₃, проведённой в построенной плоскости γ(l₁ ∩ l₂).

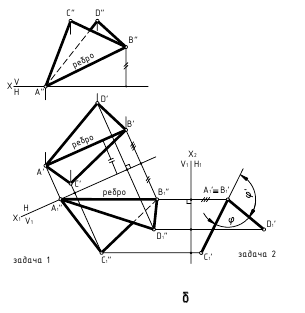
б. Если на чертеже есть ребро (линия пересечения заданных плоскостей) — угол φ определяется способом замены плоскостей проекций (задачи 1 и 2, рис. б)

ребро АВ двугранного угла преобразовать двумя заменами в проецирующую прямую.

• Тени в ортогональных проекциях
• Кривые поверхности
• Пересечения криволинейных поверхностей
• Пересечения поверхностей с прямой и плоскостью
• Пересечение поверхности плоскостью и прямой
• Развертки поверхностей
• Способы преобразования проекций
• Взаимное положение прямой и плоскости

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Способы преобразования чертежа

Содержание:

Способы преобразования чертежа можно классифицировать, исходя из основных составляющих аппарата проецирования:

• изменение положения фигур относительно основной системы координат (способ вращения относительно различных осей; способ плоскопараллельного движения);
• изменение положения плоскостей проекций (способ замены плоскостей проекций);
• изменение направления проецирования (способы дополнительного проецирования: косоугольное, окружностное, винтовое и другие).

Цель способов преобразования чертежа — приведение геометрических фигур в частное (параллельное или проецирующее) положение относительно плоскостей проекций для обеспечения большей наглядности изображения и упрощения решения позиционных и метрических задач.

Видео:Расстояние между параллельными плоскостямиСкачать

Способ замены плоскостей проекций

Смысл способа замены плоскостей проекций: при сохранении неизменного положения фигуры в пространстве вводится новая плоскость проекций, перпендикулярная одной из основных плоскостей проекций; для получения новой проекции фигуры она ортогонально проецируется на введенную плоскость проекций

Проецирование точки на вспомогательную плоскость проекций

Метрические задачи начертательной геометрии связаны с определением натуральных величин геометрических объектов. Эти величины невозможно построить ни на одной из плоскостей проекций П1, П2, П3 для произвольной ориентации объектов в пространстве: проекции отрезков короче, чем их оригиналы; проекции плоских фигур имеют искаженную форму и меньшую площадь: проекции углов, в том числе прямых, не равны действительным их значениям (рис. 2.1).

При решении позиционных задач прямым способом приходится вводить множество вспомогательных геометрических фигур, что приводит к громоздкости геометрических построений. Например, для определения линии пересечения двух плоскостей необходимо вводить вспомогательные плоскости особого положения; для построения двух взаимно перпендикулярных прямых необходимо вводить плоскость общего положения и т.д. (см. раздел 1). Это усложняет решение практических задач и чтение комплексного чертежа.

Проецирование геометрических объектов

Для устранения выше перечисленных проблем применяются способы преобразования комплексного чертежа. Одна группа этих способов связана со сменой ориентации плоскостей проекций относительно данных объектов, вторая – со сменой ориентации геометрических объектов относительно фиксированных плоскостей проекций, третья –со сменой способа проецирования. К первой группе относятся такие способы:

а) способ замены плоскостей проекций;

б) способ прямоугольного аксонометрического проецирования (см. п. 6.4),

в) способ вращения вокруг проецирующей оси (см. п. 2.2);

г) способ плоскопараллельного перемещения (см. п. 2.3);

д) способы вращения вокруг линии уровня (см. п. 2.4),

е) способ косоугольного проецирования (см. п. 2.5).

Все вышеперечисленные способы применяются для перевода геометрических объектов из общего положения в частное (положение уровня или проецирующее положение) с целью установления их взаимного расположения или для определения натуральных величин.

Суть способа замены плоскостей проекций

Способ замены плоскостей проекций состоит во введении системы дополнительных плоскостей особого положения П4, П5, …, параллельных или перпендикулярных элементам заданных геометрических объектов (плоскостей или плоских линий) с дальнейшим проецированием на эти плоскости (рис. 2.2 а, в, д) и совмещением П4, П5, … в одну плоскость (рис. 2.2 б, г, е).

Способ замены плоскостей проекций

На рис. 2.2 а – б построены четыре ортогональные проекции точки А на плоскости проекций П1, П2, П3, П4. Плоскость П4 — горизонтально-проецирующая. её горизонтальный след — одна из осей вспомогательной системы координат. Нижний индекс «14» свидетельствует о том, что прямая является линией пересечения плоскостей П1, П4. Вторая ось – фронтальный след – по направлению совпадает с осью z.

На рис. 2.2 в – г построены четыре ортогональные проекции точки А на плоскости проекций П1, П2, П3, П5. Плоскость П5 -фронтально-проецирующая. её фронтальный след — одна из осей вспомогательной системы координат. Нижний индекс «25» свидетельствует о том, что прямая является линией пересечения плоскостей П2, П5. Другая ось – горизонтальный след – по направлению совпадает с осью у.

На рис. 2.2 д – е построены четыре ортогональные проекции точки А на плоскости проекций П1, П2, П3, П6. Плоскость П6 — профильно-проецирующая. её профильный след — одна из осей вспомогательной системы координат. Нижний индекс «36» свидетельствует о том, что прямая является линией пересечения плоскостей П3, П6.Другая ось – фронтальный след –по направлению совпадает с осью х.

Правила проецирования на вспомогательные плоскости проекций:

а) проекция А4 точки А на горизонтально-проецирующую плоскость П4 находится на линии проекционной связи А1А4, перпендикулярной оси и сохраняет высоту (координату z);

б) проекция А5 точки А на фронтально-проецирующую плоскость П5 находится на линии проекционной связи А2А5, перпендикулярной оси и сохраняет глубину (координату у);

в) проекция А6 точки А на профильно-проецирующую плоскость П6 находится на линии проекционной связи А3А6,перпендикулярной оси и сохраняет ширину (координату х).

Длина отрезка и углы его наклона к плоскости проекций

Длины проекций отрезка АВ прямой общего положения на плоскости проекций П1, П2, П3 меньше действительной длины отрезка. Только прямые особого положения проецируются хотя бы на одну из плоскостей проекций в натуральную величину.

Для определения натуральной величины отрезка АВ способом замены плоскостей проекций необходимо ввести плоскость П4, параллельную этому отрезку. Проекция А4В4 — натуральная величина (рис. 2.3 а). Угол α наклона отрезка АВ к плоскости П1 равен углу наклона проекции А4В4 к оси .

На рис. 2.3 б заданы горизонтальная и фронтальная проекции отрезка АВ. Для определения натуральной величины отрезка и угла его наклона к плоскости П1 вводится вспомогательная горизонтально-проецирующая плоскость П4, параллельная отрезку АВ (ось параллельна проекции А1В1). С помощью линий проекционной связи и по координатам концов отрезка определяется проекция А4В4, являющаяся натуральной величиной АВ.

Аналогично можно определить натуральную величину отрезка путём введения дополнительной фронтально- или профильно-проецирующей плоскости П5, П6.В этом случае можно определить углы β, γ наклона отрезка к П2, П3 (рис. 2.3 в – г).

Необходимо отметить, что расстояние от отрезка до дополнительной плоскости проекций выбирается произвольно. В п. 1.4.4 показан способ прямоугольного треугольника для определения натуральной величины отрезка. Этот способ является частным случаем способа замены плоскостей проекций, в котором отрезок принадлежит вспомогательной плоскости проекций (расстояние от отрезка до вспомогательной плоскости проекций равно нулю).

Определение натуральной величины отрезка и углов его наклона к плоскостям проекций

Расстояние от точки до прямой и плоскости

Для определения расстояния от точки D до прямой l общего положения (рис. 2.4 а) необходимо ввести вспомогательную плоскость проекций П4, параллельную прямой (ось параллельна проекции l1),и найти проекции D4, l4. В таком случае прямая l занимает положения уровня относительно П4. При дальнейшем введении вспомогательной плоскости проекций П5, перпендикулярной прямой l (ось перпендикулярна проекции l4), последняя проецируется в точку l5, поскольку прямая l занимает проецирующее положения относительно П5. Проекции геометрических объектов на плоскость П5 строятся по координатам, которые определяются по системе плоскостей П1, П4. Например, расстояние h от оси до D5 равно расстоянию от оси до D1. Длина отрезка D5l5 рана расстоянию от точки D до прямой l.

Необходимо отметить, что плоскость П5 нельзя вводить сразу (без использования П4), поскольку она занимает особое положения только в системе плоскостей П4, П5, а в системе П1, П2, П3 – общее.

Определение расстояния от точки до прямой

На рис. 2.4 б прямая l задана отрезком АВ. Отрезок DN принадлежит прямой перпендикулярной l. Прямая занимает положения уровня относительно П5 (проекция D4N4 параллельна оси ). Точка N (основа перпендикуляра) является точкой пересечения двух взаимно перпендикулярных прямых n, l. Таким образом, задачу по определению расстояния от точки D до прямой l способом замены плоскостей проекций можно дополнить задачей на построение двух взаимно перпендикулярных прямых l, n ,пересекающихся в точке N.

Для определения расстояния от точки D до плоскости Σ общего положения (рис. 2.5 а) необходимо перевести плоскость Σ в проецирующее положения путём введения вспомогательной плоскости проекций П4, перпендикулярной Σ (ось перпендикулярна одной из линий уровня плоскости). В этом случае плоскость Σ проецируется в прямую Σ4, а искомое расстояние является длиной перпендикуляра D4N4, проведенного из точки D4 до прямой Σ4. Точка N — основа перпендикуляра и одновременно точка пересечения прямой заданной отрезком DN, с плоскостью Σ.

На рис. 2.5 б плоскость Σ задана треугольником АВС. Его горизонтальная прямая уровня h, заданная двумя точками А и 1, проецируется на перпендикулярную ей плоскость П4 в точку h4. Проекция А4В4С4 треугольника является отрезком, наклонённым под углом α к оси . Этот угол равен углу наклона плоскости Σ к П1. Расстояние от точки D до плоскости АВС равно длине отрезка D4N4. Горизонтальная проекция D1N1 параллельна оси и перпендикулярна горизонтальной проекции h1 горизонтали.

Определение расстояния от точки до плоскости

Расстояние между параллельными прямыми, прямой и плоскостью, двумя плоскостями

Для определения расстояния между параллельными прямыми l, m способом замены плоскостей проекций (рис. 2.6 а) вводится система двух вспомогательных плоскостей проекций П4, П5. Первая из них параллельна заданным прямым, вторая – им перпендикулярна. На плоскость П4 прямые проецируются в натуральные величины, на П5 – в точки . Длина отрезка равна расстоянию между параллельными прямыми l, m.

На рис. 2.6 б прямые заданы отрезками АВ, CD. Отрезок принадлежит прямой , перпендикулярной прямой . Прямая занимает положение уровня относительно П5 (проекция параллельна оси ). Длина отрезка равна расстоянию между параллельными прямыми l, m.

Для определения расстояния между параллельными прямой l и плоскостью Σ (рис. 2.7 а) вводится вспомогательная плоскость проекций П4, перпендикулярна Σ (ось перпендикулярна одной из линий уровня плоскости). Искомое расстояние является длиной отрезка , перпендикулярного проекциям l4, Σ4.

На рис. 2.7 б плоскость Σ задана треугольником АВС. Его горизонтальная прямая уровня h, заданная двумя точками А, 1, проецируется на перпендикулярную ей плоскость П4 в точку h4. Проекция А4В4С4 треугольника является отрезком прямой. Расстояние от прямой l до плоскости АВС равно длине отрезка . Горизонтальная проекция параллельна оси и перпендикулярна горизонтальной проекции h1 горизонтали.

Для определения расстояния между параллельными плоскостями Σ, Ω (рис. 2.8 а) вводится вспомогательная плоскость проекций П4, перпендикулярна этим плоскостям (ось перпендикулярна линии уровня одной из плоскостей). Искомое расстояние является длиной отрезка , перпендикулярного проекциям Σ4, Ω4.

На рис. 2.8 б плоскости Σ, Ω заданы своими горизонтальными и фронтальными следами. Фронтальный след плоскости Σ проецируется на перпендикулярную ей плоскость П4 в точку . Проекции Σ4, Ω4 плоскостей являются прямыми – следами построенными с помощью

Определение расстояния между параллельными прямыми

Определение расстояния между параллельными прямой и плоскостью

Определение расстояния между параллельными плоскостями

Расстояние между скрещивающимися прямыми

Для определения расстояния между скрещивающимися прямыми l, m способом замены плоскостей проекций (рис. 2.9) вводится система двух вспомогательных плоскостей проекций П4, П5. Первая из них параллельна одной из заданных прямых (например, l), вторая – перпендикулярна этой прямой. На плоскость П4 прямая l проецируется в натуральную величину, на П5 – в точку. Длина отрезка равна расстоянию между скрещивающимися прямыми l, m

На рис. 2.9 прямые заданы отрезками АВ, CD. Отрезок перпендикулярен прямым и занимает положения уровня относительно П5 (проекция параллельна оси ). Длина отрезка равна расстоянию между скрещивающимися прямыми l, m.

Определение расстояния между скрещивающимися прямыми

Угол между прямыми, прямой и плоскостью, двумя плоскостями

Натуральную величину углов между прямыми, прямой и плоскостью, двумя плоскостями невозможно определить графически по их проекциям без применения способов преобразования комплексного чертежа.

Для определения плоского угла χ между прямыми l, m, пересекающимися в точке K, способом замены плоскостей проекций необходимо спроецировать этот угол в натуральную величину. Следует ввести систему двух вспомогательных плоскостей проекций П4, П5. Первая должна быть перпендикулярна плоскости Σ, образованной данными прямыми, вторая – параллельна Σ.

На рис. 2.10 прямые l, m заданы отрезками AВ, СD. Плоскость П4 перпендикулярна фронтали f (плоскости Σ), проведенной через точки C, 1. Проекция Σ4 является отрезком прямой линии. Плоскость П5 параллельна плоскости Σ (проекция Σ4 параллельна оси ).

Определение плоского угла

Угол φ между прямой l и плоскостью Σ определяется с помощью введения вспомогательной плоскости проекций П4, перпендикулярный заданной плоскости (рис. 2.11 а). Таким образом, задача по определению угла φ между прямой l и плоскостью Σ сводится к задаче по определению угла между проекцией l4 прямой и следом Σ4 плоскости.

Угол φ между прямой l и плоскостью Σ также определяется (рис. 2.11 б) с помощью вспомогательного угла между данной прямой и прямой проходящей через произвольную точку D прямой l перпендикулярно плоскости Σ (см. п. 1.6.3, рис. 1.69). Таким образом, задача по определению угла φ между прямой l и плоскостью Σ сводится к задаче по определению вспомогательного угла между двумя прямыми (см. рис. 2.10). Из проекций D1, D2 произвольной точки прямой l проведены проекции перпендикулярные соответствующим следам плоскости Σ. С помощью вспомогательной плоскости проекций П4, перпендикулярной плоскости Ω, образованной прямыми (ось перпендикулярна проекции h1 плоскости Ω), последняя проецируется в прямую линию l4. После введения плоскости проекций П5, параллельной плоскости Ω (ось параллельна следу l4), определяется натуральная величина вспомогательного угла . Искомый угол φ дополняет вспомогательный угол до 90°.

Определение угла между прямой и плоскостью

Существуют два способа определения угла θ между двумя плоскостями Σ, Ω (см. п. 1.6.3). Прямой способ реализуется, в том числе, с помощью способа замены плоскостей проекций.

Прямой способ определения двугранного угла

На рис. 2.12 плоскости Σ, Ω заданы треугольником АВС и параллельными прямыми a, b. Прямая k — линия пересечения плоскостей (см. п. 1.5.8, рис. 1.42). С помощью вспомогательной плоскости проекций П4, параллельной прямой k, последняя переведена в положения уровня. Введение плоскости проекций П5, перпендикулярной прямой k, позволяет определить угол θ между заданными плоскостями.

При непрямом способе угол θ между плоскостями Σ, Ω равен углу между прямыми пересекающимися в произвольной точке пространства и перпендикулярны ,соответственно, плоскостям Σ, Ω (см. п. 1.6.3, рис. 1.70)..

На рис. 2.13 плоскости Σ, Ω заданы своими горизонтальными и фронтальными следами. Из проекций D1, D2 произвольной точки пространства проведены прямые и перпендикулярные соответствующим следам плоскостей.

С помощью вспомогательной плоскости проекций П4, перпендикулярной вспомогательной плоскости Ψ, заданной прямыми плоскость Ψ переведена в проецирующее положение. После введения плоскости проекций П5, параллельной плоскости Ψ, определяется угол , числовое значение которого совпадает с искомым углом θ.

Непрямой способ определения двугранного угла

Натуральная величина плоской фигуры

Натуральная величина плоской фигуры определяется как без применения способов преобразования комплексного чертежа, так и с их применением.

На рис. 2.14 показан способ определения натуральной величины треугольника АВС способом прямоугольного треугольника (см. п. 1.4.4). Предварительно определяются натуральные величины сторон АВ, ВС, АС. На их основе строится треугольник А0В0С0, тождественный натуральной величине треугольника АВС

Для определения натуральной величины плоской фигуры Ф способом замени плоскостей проекций (рис. 2.15 а) необходимо ввести по очереди плоскость П4, перпендикулярную Ф, и П5, параллельную Ф (ось параллельная следу плоской фигуры на плоскости П4). Проекция Ф5 является натуральной величиной фигуры Ф.

На рис. 2.15 б плоская фигура является треугольником АВС. Ось вспомогательной системы плоскостей П1, П4 перпендикулярна фронтальной проекции фронтали f треугольника. Проекция А4В4С4 является отрезком прямой линии. Ось вспомогательной системы плоскостей П4, П5 параллельна проекции А4В4С4. Проекция А5В5С5 является натуральной величиной треугольника АВС.

Определение натуральной величины плоской фигуры способом прямоугольного треугольника

Определение натуральной величины плоской фигуры способом замены плоскостей проекций

Пересечение прямой и плоскости, двух плоскостей

У п. 1.5.7 показан способ определения точки K пересечения прямой l и плоскости Σ с помощью вспомогательной плоскости Ω особого положения (рис. 1.38).

Для определения точки K пересечения прямой l с плоскостью Σ способом замены плоскостей проекций (рис. 2.16) вводится вспомогательная плоскость П4, перпендикулярная плоскости Σ. На П4 последняя проецируется в прямую Σ4. Точка K4 пересечения Σ4, l4 позволяет определить горизонтальную и фронтальную проекции точки K пересечения прямой l с плоскостью Σ.

Определение точки пересечения прямой и плоскости

На рис. 2.16 плоскость Σ задана треугольником АВС, прямая l – точками 2, 3. На плоскости построена фронталь f, которой перпендикулярна вспомогательная плоскость проекций П4. Точка K пересечения прямой и плоскости имеет проекцию K4, которая является точкой пересечения отрезков .

У п. 1.5.8 показаны три способа определения линии пересечения двух плоскостей (рис. 1.42 – 1.46), не связанные с преобразованиями комплексного чертежа.

Определение линии пересечения плоскостей

Для определения линии MN пересечения двух плоскостей Σ, Ω способом замены плоскостей проекций (рис. 2.17) вводится вспомогательная плоскость П4, перпендикулярная плоскости Σ, на которую последняя проецируется в прямую Σ4. Прямая M4N4 пересечения Σ4, Ω4 позволяет определить горизонтальную и фронтальную проекции линии пересечения данных плоскостей .

На рис. 2.17 плоскости Σ, Ω заданы треугольниками АВС, DEF. В первом проведена фронталь f, которой перпендикулярна вспомогательная плоскость проекций П4. Линия пересечения плоскостей АВС, DEF имеет проекцию М4N4, принадлежащую проекции А4В4С4.

Видео:Способ замены (перемены) плоскостей проекции. Определение истинной величины отрезка и плоской фигурыСкачать

Способ вращения вокруг проецирующей оси

Метод вращения вокруг проецирующих осей этот метод заключается в том, что геометрический объект (прямую или плоскость) вращают вокруг проецирующей оси i до положения параллельности какой-либо плоскости проекций. В результате вращения геометрический объект проецируется на плоскость проекций в натуральную величину.

Вращение точки вокруг проецирующей оси

Способ вращения вокруг проецирующей оси — это один из способов преобразования комплексного чертежа, в котором геометрический объект вращается вокруг проецирующей оси до тех пор, пока не займет особое положение (рис. 2.18).

Поскольку любой геометрический объект является совокупностью точек в пространстве, для его вращения вокруг оси необходимо уметь вращать каждую точку.

На рис. 2.19 показан комплексный чертёж точки А до и после вращения вокруг осей i, j соответственно на углы α, β.

Вращение вокруг проецирующей оси

Реализация способа вращения вокруг проецирующей оси

Для вращения точки А вокруг проецирующей оси необходимо знать:

а) ось вращения– прямая линия, которая не изменяет своего положения в пространстве во время вращательного движения точки;

б) центр вращения – точка на оси вращения, для которого выполняется условие перпендикулярности отрезку оси вращения;

в) радиус вращения r – расстояние от центра вращения до точки А;

г) направление вращения;

Траекторией точки А при её вращении вокруг проецирующей оси является дуга окружности, принадлежащей плоскости уровня. Проекция траектории на одну из плоскостей проекций является дугой окружности, на две другие – прямой, параллельной соответствующим осям координат (рис. 2.19).

Способом вращении вокруг проецирующей оси можно определить :

а) натуральную величину отрезка (см. п. 2.2.2);

б) расстояния между геометрическими объектами (см. пп. 2.2.3 – 2.2.5);

в) точку пересечения прямой и плоскости (см. п. 2.2.6);

г) линию пересечения двух плоскостей (см. п. 2.3.5);

д) точки пересечения прямой линии с поверхностью тела вращения (см. п. 4.2.2.3).

Длина отрезка

Задача по определению натуральной величины отрезка имеет простейший способ реализации с использованием способа вращения вокруг проецирующей оси .

На рис. 2.20 приведён пример определения длины отрезка АВ общего положения. Через точку А проведена фронтально-проецирующая ось j, вокруг которой данный отрезок вращается до положения горизонтального уровня (фронтальная проекция параллельная оси х). Горизонтальная проекция является натуральной величиной отрезка АВ

Определение длины отрезка

Расстояние от точки до прямой и плоскости

Для определения расстояния от точки А до прямой l общего положения способом вращения вокруг проецирующей оси необходимо повернуть прямую до положения уровня.

На рис. 2.21 прямая l задана отрезком ВС. Фронтально-проецирующая ось вращения j проходит через точку В. Точки А, С вращаются вокруг оси на одинаковый угол. После вращения отрезок ВС занимает горизонтальное положение уровня По теореме о проецировании прямого угла (см. п. 1.4.8, рис. 1.26) горизонтальная проекция перпендикуляра, проведенного из точки к отрезку , проецируется на П1 в натуральную величину. Натуральная величина отрезка АN определяется путём вращения отрезка вокруг фронтально-проецирующей оси и равна длине отрезка

Определение расстояния от точки до прямой

Определение расстояния от точки до плоскости

Для определения расстояния от точки D до плоскости Σ общего положения способом вращении вокруг проецирующей оси необходимо повернуть плоскость в проецирующее положение.

На рис. 2.22 плоскость Σ задана треугольником АВС. Плоскости принадлежит фронталь f, проведенная через точки В, 1. Фронтально-проецирующая ось вращения j проходит через точку В. Точки А, С, D вращаются вокруг оси j на одинаковый угол. После вращения прямая f занимает горизонтально-проецирующее положение, а треугольник проецируется на П1 в отрезок прямой. Длина перпендикуляра , проведенного к плоскости , равна расстоянию от точки D к плоскости Σ.

Расстояние между параллельными прямыми, прямой и плоскостью, двумя плоскостями

Для определения расстояния между параллельными прямыми l, m способом вращения вокруг проецирующей оси прямые l, m вращаются вокруг этой оси до положения уровня.

На рис. 2.23 прямые заданные отрезками АВ, CD. Прямые вращаются вокруг фронтально-проецирующей оси j, яка проходить через точку А, до горизонтального положения уровня. На горизонтальной плоскости проекций П1 проекция перпендикуляра к образует прямые углы с проекциями . Расстояние между параллельными прямыми равно длине отрезка и определяется способом вращения вокруг проецирующей оси (равно длине отрезка

Для определения расстояния между параллельными прямой l и плоскостью Σ способом вращения вокруг проецирующей оси плоскость Σ вращается вокруг проецирующей оси до проецирующего положения.

Определение расстояния между параллельными прямыми

Определение расстояния между параллельными прямой и плоскостью

На рис. 2.24 плоскость Σ задана треугольником АВС, прямая l – отрезком DE. Фронталь f плоскости АВС, задана двумя точками В, 1, после вращения вокруг проецирующей оси j, проходящей через точку В, проецируется на плоскость П1 в точку у . Проекция треугольника является отрезком прямой. Расстояние от прямой l до плоскости АВС равно длине отрезка

Для определения расстояния между параллельными плоскостями Σ, Ω последние вращаются вокруг проецирующей оси до проецирующего положения.

На рис. 2.25 плоскости Σ, Ω заданы треугольниками АВС, DEF. Фронталь f плоскости АВС задана двумя точками В, 1. После вращения вокруг проецирующей оси j, проходящей через точку В, фронталь f проецируется на плоскость П1 в точку . Проекции треугольников являются отрезками прямых. Расстояние между данными плоскостями равно длине перпендикуляра

Определение расстояния между параллельными плоскостями

Расстояние между скрещивающимися прямыми

Для определения расстояния между скрещивающимися прямыми l, m применяется способ вспомогательной параллельной плоскости (см. п. 1.6.2, рис. 1.65 – 1.66), для чего вводится плоскость Σ, проходящая через прямую параллельно прямой l. После вращения вокруг проецирующей оси плоскость Σ проецируется в прямую линию. Расстояние между этой линией и соответствующей проекцией прямой l равен расстоянию между скрещивающимися прямыми.

Определение расстояния между скрещивающимися прямыми

На рис. 2.26 прямые l, m заданы отрезками АВ, CD. Вспомогательная плоскость Σ, задана треугольником CDE, параллельна отрезку АВ. После вращения вокруг горизонтально-проецирующей оси и, проходящая через точку D, треугольник CDE занимает фронтально-проецирующее положение . Длина перпендикуляра равна расстоянию между прямыми l, m.

Пересечение прямой и плоскости

Для определения точки K пересечения прямой l и плоскости Σ последняя вращается вокруг проецирующей оси до проецирующего положения. На рис. 2.27 плоскость задана треугольником АВС, прямая – отрезком DE. В плоскости построена фронталь f, которая после вращения вокруг фронтально-проецирующей оси j переводится в горизонтально-проецирующую прямую f . При этом плоскость проецируется в прямую , пересекающую проекцию в точке . Вращение этой точки вокруг оси j в обратном направлении позволяет определить искомые проекции K1, K2.

Определение точки пересечения прямой и плоскости

Видео:Видеоурок "Расстояние между прямыми в пространстве"Скачать

Способ плоскопараллельного перемещения

Способ плоскопараллельного перемещения основан на том, что при параллельном переносе геометрического тела относительно плоскости проекций проекция его на эту плоскость не меняет своей формы и размеров, хотя и меняет положение.

Плоскопараллельное перемещение тела

Плоскопараллельным движением тела называется такое его движение, в котором все точки тела имеют траектории, принадлежащие плоскостям, параллельным некоторой неподвижной плоскости. Последней в начертательной геометрии выбирают одну из плоскостей проекций.

Плоскопараллельные перемещения

Способ плоскопараллельного перемещения каждой точки тела реализуется с помощью комбинации двух движений: поступательного движения проецирующей оси и вращения вокруг этой оси (рис. 2.28).Целью применения способа плоскопараллельного перемещения является переведение геометрических объектов из общего положения в особое.

Способ вращения вокруг проецирующей оси (см. п. 2.2) является частным случаем способа плоскопараллельного перемещения, в котором ось вращения неподвижна.

Реализация способа плоскопараллельного перемещения тела Ф на его комплексном чертеже приведена на рис. 2.29. Она аналогична вращению вокруг проецирующей оси, но имеет существенное преимущество: одну из проекций объекта (на рис. 2.29 – это фронтальная проекция) можно переносить на свободное поле комплексного чертежа.

Основное правило плоскопараллельного перемещения

При плоскопараллельном перемещении геометрического объекта расстояния между всеми парами его точек не изменяются.

На рис. 2.29 длины проекций отрезков одинаковы так же, как одинаковы длины проекций отрезков и т.д..

Правило определения видимости для способа плоскопараллельного перемещения

При плоскопараллельном перемещении геометрического объекта видимость его линий не изменяется на одной из плоскостей проекций.

На рис. 2.29 на фронтальной проекции отрезок ВD невидим, все другие – видимы. После плоскопараллельного перемещения тела видимость отрезков на фронтальной проекции не изменилась, на горизонтальной – изменилась для отрезков AD, CD.

Способом плоскопараллельного перемещения решаются все задачи, описанные в п. 2.2, а также и те, которые не целесообразно решать способом вращения вокруг проецирующей оси.

Реализация способа плоскопараллельного перемещения

Расстояние между скрещивающимися прямыми

Расстояние между скрещивающимися прямыми определяется такими способами:

а) вспомогательной параллельной плоскости (см. п. 1.6.2, рис. 1.65 – 1.66);

б) замены плоскостей проекций (п. 2.1.5, рис. 2.9);

в) вращения вокруг проецирующей оси (п. 2.2.5, рис. 2.26);

г) плоскопараллельного перемещения.

Способом параллельного перемещения можно определить расстояние между скрещивающимися прямыми l, m путём проецирования одной из прямых в точку.

На рис. 2.30 прямые l, m заданы отрезками АВ, CD. Их перемещение, параллельное плоскости П2, дозволяет перевести прямую l в горизонтальное положение уровня (проекция параллельна оси х; длина проекции является натуральной величиной отрезка АВ). Перемещение отрезков , параллельное плоскости П1, позволяет спроецировать прямую во фронтально-проецирующее положение (проекция перпендикулярна оси х; проекция является точкой). Расстояние между скрещивающимися прямыми l, m равно длине проекции перпендикуляра .

Определение расстояния между скрещивающимися прямыми

Угол между прямыми, прямой и плоскостью, двумя плоскостями

Для определения угла χ между двумя прямыми l, m, пересекающимися в точке K, способом плоскопараллельного перемещения необходимо перевести плоскость Σ,образованную этими прямыми , сначала в проецирующее положение, а потом – в положение уровня.

На рис. 2.31 прямые l, m заданы отрезками АВ, CD. В плоскости Σ, заданной прямыми l, m, вводится горизонталь h, которая с помощью перемещения, параллельного П1, переводится во фронтально-проецирующее положение (проекция перпендикулярна оси х; проекция является точкой; проекция является прямой линией). Перемещение плоскости параллельно плоскости П2 позволяет спроецировать угол χ между прямыми l, m в натуральную величину.

Определение плоского угла

Угол φ между прямой l и плоскостью Σ и между двумя плоскостями определяется с помощью перемещения плоскости Σ параллельно одной из плоскостей проекций до проецирующего положения.

На рис. 2.32 плоскость Σ задана треугольником АВС, прямая l – отрезком DE. В плоскости Σ проведена горизонтальная прямая уровня h, которая после плоскопараллельного перемещения проецируется в точку , а треугольник – на отрезок прямой. Угол φ между фронтальными проекциями равен искомому углу φ между прямой l и плоскостью Σ.

Определение угла между прямой и плоскостью

На рис. 2.33 плоскости Σ, Ω заданы треугольниками АВС, ABD. С помощью перемещения отрезка АВ (основы двугранного угла) параллельно П2, данный отрезок проецируется на П1 в натуральную величину. Перемещение отрезка параллельно П1 позволяет спроецировать заданные плоскости в прямые линии, пересекающиеся в точке, и определить угол θ между ними. Этот угол равен искомому двугранному углу при ребре АВ.

Определение двугранного угла

Натуральная величина плоской фигуры

Для определения натуральной величины плоской фигуры Ф способом плоскопараллельного перемещения необходимо перевести эту фигуру в положение уровня, перед этим спроецировав её на отрезок прямой линии.

На рис. 2.34 фигура Ф является треугольником АВС. В нём вводится горизонталь h, которая с помощью перемещения, параллельного П1, переводится во фронтально-проецирующее положение (проекция перпендикулярна оси х; проекция является точкой; проекция является отрезком прямой). Перемещение фигуры параллельно плоскости П2 позволяет определить натуральную величину треугольника АВС.

Определение натуральной величины плоской фигуры

Пересечение плоскостей

Для определения линии k (отрезка MN) пересечения двух плоскостей Σ, Ω способом плоскопараллельного перемещения одна из плоскостей переводится в проецирующее положение.

На рис. 2.35 плоскости заданы треугольниками АВС, DEF. В первом проведена горизонталь h, которая перемещается параллельно П1 до фронтально-проецирующего положения (проекция перпендикулярна оси х; проекция является точкой). При этом треугольник проецируется на отрезок который совпадает с проекцией линии пересечения, заданной точками . Искомые горизонтальная и фронтальная проекции отрезка MN определяются по линиям проекционной связи.

Определение линии пересечения плоскостей

Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Способ вращения вокруг линии уровня

При применении метода поворота плоскость проекции не изменяется, и изменяется исходное положение в пространстве. Изменение исходного положения осуществляется вращением Он вокруг оси. Линия проекции уровня или прямая линия обычно выбирается в качестве оси вращения.

Вращение точки вокруг линии уровня

Способ вращения вокруг линии уровня является одним из способов преобразования комплексного чертежа, в котором геометрический объект вращается вокруг линии уровня до тех пор, пока не займет особое положение (рис. 2.36).

На рис. 2.37 а показаны положения точки В до и после вращения вокруг горизонтальной прямой уровня.

Вращение вокруг линии уровня

Реализация способа вращения вокруг линии уровня

Для вращения точки В вокруг прямой уровня необходимо знать:

а) ось вращения – горизонталь, фронталь или профильная прямая уровня;

б) центр вращения – точка на оси вращения, для которой выполняется условие перпендикулярности отрезка оси вращения;

в) радиус вращения r – расстояние от центра вращения до точки В;

г) направление вращения.

Траекторией точки В при её вращении вокруг линии уровня является окружность, принадлежащая проецирующей плоскости. Проекция траектории на одну из плоскостей проекций является отрезком, перпендикулярным соответствующей проекции линии уровня (рис. 2.37 б).

На рис. 2.37 отрезок общего положения вращается вокруг горизонтали h до положения горизонтального уровня. Из горизонтальной проекции точки В проведена проекция r1 радиуса вращения, перпендикулярная оси h. На горизонтальной плоскости проекций прямой угол с основой проецируется в натуральную величину (по теореме о проецировании прямого угла, см. п. 1.4.8). Точка является центром вращения точки В. С помощью линии проекционной связи определяются фронтальные проекции центра вращения и радиуса вращения. С помощью способа вращения вокруг фронтально-проецирующей оси определяется натуральная величина радиуса вращения r (отрезок ), равная длине отрезка . Новое положение точки В (после вращения вокруг горизонтали h) удалено от центра вращения на величину радиуса вращения.

Способом вращения вокруг линии уровня целесообразно решать задачу на нахождение натуральной величины плоской фигуры и плоского угла – угла между двумя прямыми, пересекающимися в точке.

Натуральная величина плоской фигуры и плоского угла

Для определения натуральной величины плоской фигуры Ф необходимо повернуть её вокруг линии уровня до положения уровня.

На рис. 2.38 задан треугольник АВС. Определение его натуральной величины реализуется с помощью вращения вокруг горизонтали h, проходящей через его точки Из горизонтальной проекции точки В проведена проекция r1 радиуса вращения, перпендикулярная оси h. На горизонтальной плоскости проекций прямой угол с основой проецируется в натуральную величину. Точка является центром вращения точки В. С помощью линии проекционной связи определяются фронтальные проекции центра и радиуса вращения. С помощью способа вращения вокруг фронтально-проецирующей оси определяется натуральная величина отрезка , равная длине отрезка . Положение точки В (после вокруг горизонтали h) удалено от центра вращения на величину радиуса вращения r. Поскольку точки А, 1 принадлежат оси вращения, они остаются неподвижными. Точка является точкой пересечения лучей (точка является центром вращения точки С; отрезок перпендикулярен h1).

Определение натуральной величины плоской фигуры

На рис. 2.38 показана натуральная величина плоского угла χ при вершине А.

Способ совмещения

Способ совмещения является частным случаем способа вращения вокруг линии уровня. Осью вращения в нём является след плоскости, которой принадлежит плоская фигура.

Способ совмещения используется для нахождения натуральной величины плоской фигуры. В результате вращения последняя совмещается с одной из плоскостей проекций (рис. 2.39 а).

На рис. 2.39 б показана реализация способа совмещения плоскости Σ общего положения с горизонтальной плоскостью проекций П1. На фронтальном следе произвольно выбрана точка . Горизонтальная проекция точки 1 принадлежит оси х. Высота точки 1 равна . Центром вращения точки 1 вокруг горизонтального следа вращения плоскости Σ является точка . Натуральная величина r радиуса вращения равна длине отрезка 1. Величина радиуса вращения откладывается вдоль направления вращения Через точки строится новое положение фронтального следа. Таким образом, после вращения вокруг горизонтального следа плоскость Σ совмещается с горизонтальной плоскостью проекций П1.

Способ совмещения

На рис. 2.40 определена натуральная величина четырехугольника АВСD, принадлежащего плоскости Σ, заданной горизонтальным и фронтальным следами . Точки А, В, С, D вращаются вокруг горизонтального следа Для определения нового положения из точки А проводится горизонталь h и определяются точки Точка принадлежит новому положению горизонтали. Аналогично определяются точки . После вращения натуральная величина четырехугольника принадлежит плоскости проекций П1.

Определение натуральной величины плоской фигуры способом совмещения

Видео:7 класс, 38 урок, Расстояние от точки до прямой. Расстояние между параллельными прямымиСкачать

Способ косоугольного проецирования

Изображения предметов на чертежах получают проецированием. Проецирование – это процесс получения изображения предмета на какой-либо поверхности . Получившееся при этом изображение называют проекцией предмета. Слово «проекция» в переводе с латинского означает «бросание вперед, вдаль».

Косоугольное проецирование на ортогональные плоскости проекций

Косоугольное проецирование — один из видов параллельного проецирования (см. п. 1.1.2.1, рис. 1.3), в котором проецирующие лучи не перпендикулярны плоскостям проекций П1, П2, П3.

Косоугольное проецирование задаётся направлением проецирования і, которое в общем случае направлено вдоль линии общего положения.

В начертательной геометрии используются три вида косоугольного проецирования:

а) на ортогональные плоскости проекций П1, П2, П3;

б) на плоскость особого положения (см. п. 2.5.2);

в) на биссекторную плоскость (см. п. 2.5.3).

Использование косоугольного проецирования направлено на искажение изображения геометрического объекта с целью упрощения его формы (прямая проецируется в точку, плоскость – в прямую и т.д.).

Правило косоугольного проецирования точки на ортогональные плоскости проекций

При косоугольном проецировании точки А на одну из плоскостей проекций П1, П2, П3 косоугольная проекция совпадает с соответствующим следом (см. п. 1.4.3, рис. 1.12) проецирующего луча і (рис. 2.41 а). Горизонтальная проекция точки принадлежит оси х, фронтальная – совпадает с косоугольной проекцией . Линии косоугольного проецирования параллельны соответствующим проекциям проецирующего луча і.

На рис. 2.41 б построен комплексный чертёж точки А и её косоугольной проекции А на фронтальную плоскость проекций П2.

Косоугольное проецирование на плоскость проекций

Способ косоугольного проецирования позволяет относительно быстро решать позиционные задачи на пересечение геометрических объектов (прямой и плоскости, двух плоскостей и т.д.).

На рис. 2.42 построена точка K пересечения прямой l с плоскостью Σ, заданной параллельными прямыми а, b. Введен проецирующий луч і, параллельный заданной плоскости. Косоугольная проекция плоскости Σ на плоскость проекций П2 (прямая ) является фронтальным следом плоскости Σ и пересекается с косоугольной проекцией в точке . С помощью линий проекционной связи определяются фронтальная и горизонтальная проекции искомой точки K.

Определение точки пересечения прямой и плоскости

На рис. 2.42 с целью упрощения горизонтальные проекции плоскости и прямой не обозначены (они совпадают с осью х). Их фронтальные проекции совпадают с косоугольными проекциями, поэтому нижний индекс «2» также не обозначен.

На рис. 2.43 построена линия k пересечения плоскости Σ, заданной параллельными прямыми а, b, с плоскостью Ω, заданной треугольником АВС. Введен проецирующий луч і, параллельный плоскости Σ. Косоугольная проекция плоскости Σ на плоскость проекций П2 (пряма ) является фронтальным следом плоскости Σ и пересекается с косоугольной проекцией по прямой , заданной отрезком . С помощью линий проекционной связи определяются фронтальная и горизонтальная проекции искомой прямой k.

Определение линий пересечения плоскостей

Косоугольное проецирование на плоскость особого положения

При косоугольном проецировании на плоскость особого положения (плоскость уровня или проецирующую плоскость) вводится вспомогательная плоскость с помощью одного из своих следов .

На рис. 2.44 а показан способ косоугольного проецирования на горизонтально-проецирующую плоскость . На рис. 2.44 б построен комплексный чертёж точки А, косоугольно спроецированной на эту плоскость. Горизонтальная проекция является точкой пересечения оси с горизонтальной проекцией проецирующего луча. Фронтальная проекция является точкой пересечения фронтальной проекции проецирующего луча с вертикальной линией проекционной связи, проведенной из точки .

Косоугольное проецирование на проецирующую плоскость

На рис. 2.45 построена точка K пересечения прямой l с плоскостью Σ, заданной параллельными прямыми а, b. Введены горизонтально-проецирующая плоскость и проецирующий луч і, параллельный плоскости Σ. Косоугольная проекция плоскости Σ на плоскость проекций П2 является прямой пересекающейся с косоугольной проекцией в точке С помощью линий проекционной связи определяются фронтальная и горизонтальная проекции искомой точки K.

Определение точки пересечения прямой и плоскости

На рис. 2.45 для упрощения горизонтальные проекции плоскости и прямой не обозначены (они совпадают с осью ). Их фронтальные проекции не совпадают с проекциями на плоскость поэтому нижний индекс «2» обязателен.

На рис. 2.46 построена линия k пересечения плоскости Σ, заданной параллельными прямыми а, b, с плоскостью Ω, заданной треугольником АВС. Введены горизонтально проецирующая плоскость и проецирующий луч і, параллельный плоскости Σ. Косоугольная проекция плоскости Σ на плоскость проекций П2 пересекается с косоугольной проекцией плоскости Ω по прямой заданной отрезком С помощью линий проекционной связи определяются фронтальная и горизонтальная проекции искомой прямой k.

Определение линии пересечения плоскостей

Косоугольное проецирование на биссекторную плоскость

Биссекторная плоскость – это плоскость, равнонаклонённая к двум плоскостям проекций. При решении позиционных задач на пересечение геометрических объектов используются способы косоугольного проецирования, в том числе на биссекторную плоскость которая проходит через ось х, принадлежит ІІ и ІV четвертям (см. п. 1.3.1, рис. 1.6) и наклонена к плоскостям проекций П1, П2 под углом 45° (рис. 2.47 а).

Биссекторная плоскость

Основное свойство точек биссекторной плоскости

Любая точка А биссекторной плоскости имеет одинаковые по модулю и противоположные по знаку высоту z и глубину у (рис. 2.47).

На рис. 2.47 б построен комплексный чертёж точки А и её косоугольной проекции на биссекторную плоскость

Согласно основному свойству биссекторной плоскости на комплексном чертеже вместо обозначения косоугольных проекций которые совпадают , упрощенно обозначается только (рис. 2.48).

Косоугольное проецирование точки на биссекторную плоскость

Правило определения косоугольной проекции точки на биссекторную плоскость

Косоугольная проекция точки А на биссекторную плоскость является точкой пересечения горизонтальной и фронтальной проекций проецирующего луча і (рис. 2.48).

На рис. 2.49 построена точка K пересечения прямой l с плоскостью Σ, заданной параллельными прямыми а, b. Введен проецирующий луч і, параллельный заданной плоскости. Косоугольная проекция плоскости Σ на биссекторную плоскость П2 является прямой пересекающейся с косоугольной проекцией в точке С помощью линий проекционной связи точки на биссекторную плоскость определяются фронтальная и горизонтальная проекции точки K.

Определение точки пересечения прямой и плоскости

На рис. 2.50 построена линия k пересечения плоскости Σ, заданной параллельными прямыми а, b, с плоскостью Ω, заданной треугольником АВС. Введен проецирующий луч і, параллельный плоскости Σ. Косоугольная проекция плоскости Σ на биссекторную плоскость является прямой пересекающейся с косоугольной проекцией плоскости Ω по прямой заданный отрезком С помощью линий косоугольной проекционной связи определяются фронтальная и горизонтальная проекции искомой прямой k.

Определение линий пересечения плоскостей

Видео:Определение кратчайшего расстояния между скрещивающимися прямыми (Способ замены плоскостей проекций)Скачать

Комбинированные способы

Описанные в разделах 1, 2 способы позволяют решать большое количество позиционных и метрических задач начертательной геометрии. При этом одну задачу можно решать разными способами, которые отличаются сложностью реализации. Поэтому, прежде, чем решать ту или иную задачу, необходимо проанализировать и сравнить между собой разные способы по критерию их сложности. Субъективное мнение авторов по этому вопросу приведено в табл. 2.1.

Таблица 2.1- Способы решения задач начертательной геометрии

Из табл. 2.1 видим, что универсальным способом решения почти всех задач начертательной геометрии является способ замены плоскостей проекций.

При решении комплексных задач способ замены плоскостей проекций можно дополнять другими способами (например, вращение вокруг проецирующей оси і, плоскопараллельного перемещения и т.д.). Умение объединять разные способы свидетельствует о высоком уровне опытности будущего инженера .

На рис. 2.51 определена натуральная величина треугольника АВС с использованием комбинации двух способов – замены плоскостей проекций и плоскопараллельного перемещения. На рис. 2.52 комбинацией двух указанных способов определён двугранный угол θ при ребре АВ.

Определение натуральной величины плоской фигуры

Определение двугранного угла

Примеры и образцы решения задач:

Услуги по выполнению чертежей:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

🔍 Видео

Определение кратчайшей расстоянии от точки до плоскостиСкачать

Определить кратчайшее расстояние между ребрами AB и SC. Замена плоскостей проекцииСкачать

Расстояние между скрещивающимися прямыми за 1 минуту. #математикапрофиль2023 #егэ2023 #школа #fypСкачать

Геометрия 7 класс (Урок№26 - Расстояние от точки до прямой. Расстояние между параллельными прямыми.)Скачать

Замена плоскостей проекции(Расстояние от точки до прямой)Скачать