Радиусы двух пересекающихся окружностей равны 17

Видео:Математика Радиусы двух пересекающихся окружностей равны 17 см и 39 см, а расстояние между ихСкачать

Ваш ответ

Видео:Планиметрия 12 | mathus.ru | расстояние между центрами пересекающихся окружностейСкачать

решение вопроса

Видео:Задание 24 Две пересекающиеся окружностиСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,929
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Задача про две вневписанные окружности | ЕГЭ. Задание 16. Математика | Борис Трушин |Скачать

Радиусы двух пересекающихся окружностей равны 17 см и 39 см, а расстояниемежду их центрами – 44 см?

Математика | 5 — 9 классы

Радиусы двух пересекающихся окружностей равны 17 см и 39 см, а расстояние

между их центрами – 44 см.

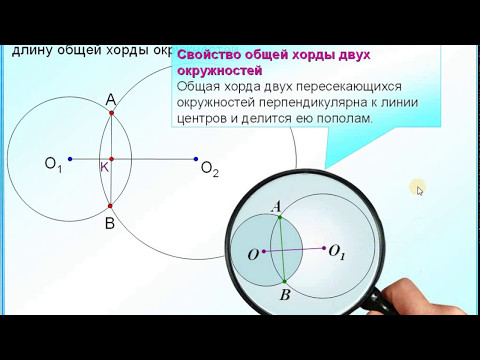
Найдите длину общей хорды окружностей.

Расстояние между центрами O1O2 = 44 см.

Расстояния от центра окружности до хорды O1C = x см, O2C = 44 — x см.

Длина хорды AB = a см ; AC = BC = a / 2 см.

По теореме Пифагора

Подставляем известные величины

Подставляем 1 уравнение во 2 уравнение

1936 — 88x + 289 = 1521

x = (1936 + 289 — 1521) / 88 = 704 / 88 = 8

Подставляем это в 1 уравнение

8 ^ 2 + a ^ 2 / 4 = 289

a ^ 2 = (289 — 64) * 4 = 225 * 4 = 900

Видео:Планиметрия 11 |mathus.ru|  расстояние между центрами пересекающихся окружностейСкачать

Длина хорды окружности равна 120, а расстояние от центра окружности до этой хорды равно 45?

Длина хорды окружности равна 120, а расстояние от центра окружности до этой хорды равно 45.

Найдите диаметр окружности.

Видео:Найти радиус окружности если известны длины пересекающихся хордСкачать

Хорда, равная 18 см, отсекает от окружности дугу в 90 * ?

Хорда, равная 18 см, отсекает от окружности дугу в 90 * .

Найдите расстояние от центра окружности до хорды.

Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

В окружности с центром О и радиусом 6 см и перпендикулярные радиусы ОА и ОB Чему равна длина хорды AB?

В окружности с центром О и радиусом 6 см и перпендикулярные радиусы ОА и ОB Чему равна длина хорды AB?

Видео:ОГЭ по математике. 9 класс. Задача 26. Вариант 5.Скачать

Отрезки АВ и СD является хордами окружности?

Отрезки АВ и СD является хордами окружности.

Найдите расстояние от центра окружности до хорды СD, если АВ = 40 , CD = 42, а расстояние от центра окружности до хорды АВ равна 21.

Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

ДАНА ОКРУЖНОСТЬ?

НАЙДИТЕ РАССТОЯНИЕ ОТ ЦЕНТРА ОКРУЖНОСТИ ДО ХОРДЫ AB ЕСЛИ AB 8 СМ , А РАДИУС 5 СМ.

Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Расстояние между центрами двух равных окружностей 10см?

Расстояние между центрами двух равных окружностей 10см.

Каков должен быть радиус этих окружностей , чтобы они имели только одну общую точку?

Видео:Без этих теорем ты не затащишь геометрию на ЕГЭ. Задача 17 счетная планиметрияСкачать

ДАНА ОКРУЖНОСТЬ?

НАЙДИТЕ РАССТОЯНИЕ ОТ ЦЕНТРА ОКРУЖНОСТИ ДО ХОРДЫ AB ЕСЛИ AB 8 СМ , А РАДИУС 5 СМ.

Видео:Геометрия Общая хорда двух пересекающихся окружностей видна из их центров под углами 90 и 60. НайтиСкачать

Радиусы двух окружностей равны 3 сантиметра и 5 сантиметров а расстояние между наиболее удаленными точками этих окружностей равно 18 см Найдите расстояние между центрами окружностей?

Радиусы двух окружностей равны 3 сантиметра и 5 сантиметров а расстояние между наиболее удаленными точками этих окружностей равно 18 см Найдите расстояние между центрами окружностей.

Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Центр окружности S1 с радиусом 7, 5 см находится на расстоянии 4, 5 см от оси симметрии m?

Центр окружности S1 с радиусом 7, 5 см находится на расстоянии 4, 5 см от оси симметрии m.

При симметрии относительно оси m окружности S1 переходит в окружности S2.

Найдите длину общей хорды окружности S1 и S2?

Видео:Внутреннее сопряжение двух дуг окружностей третьей дугой. Урок14.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Начертит две окружности с общим центром?

Начертит две окружности с общим центром.

Радиус большой окружности 4 см а меньшей 4 см.

Проведи отрезок, пересекающий каждую из окружностей в двух точках.

Видео:ЕГЭ Задача 16 Пересекающиеся окружностиСкачать

Одна из двух равных окружностей проходит через центр другой окружности?

Одна из двух равных окружностей проходит через центр другой окружности.

Вычисли длину общей хорды, если радиус окружности равен 18 м.

На странице вопроса Радиусы двух пересекающихся окружностей равны 17 см и 39 см, а расстояниемежду их центрами – 44 см? из категории Математика вы найдете ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

Четырехугольник является ромбом, если его стороны равны, а диагонали не равны и взаимно перпендикулярны. Имеем вершины : А(3 ; 5 ; 4), В(5 ; 0 ; 2), С(1 ; 1 ; — 2) и Д ( — 1 ; 6 ; 0). Находим длины сторон : АВ = √((Хв — Ха)² + (Ув — Уа)² + (Zв — Zа..

4x + 3y + 6 = 0, 8x + 6y — 7 = 0 → 4x + 3y — 7 / 2 = 0 |4x + 3y — 7 / 2 — (4x + 3y + 6)| = | — 7 / 2 — 6| = 19 / 2.

(92 — 12) : 4 — 12 — на столько тетрадь дороже ручки.

(92 — 12) : 4 — 12 = 8 руб настолько дороже тетрадь.

Х — 80 = 280 + 2 х — 80 = 282 х = 282 + 80 х = 362.

Решим уравнение х = 362 Ответ : х = 362.

1) 45 : 3 = 15(км) — изначальная скорость вороны 2) 15 * 8 = 120 (км) за 8 секунд 3) 75 : 15 = 5(сек) Ответ : за 5 секунд пролетит ворона 75 м и за 8 секунд 120 км пролетит ворона.

75 ; 150 ; 225 ; 300 ; 375 ; 450 ; 525 ; 600 ; 675 ; 750 ; 825 ; 900 ; 975.

641, 62 (считала на калькуляторе) : ).

1) 8, 4 * 0, 55 = 4, 62 2) 4, 62 + 3, 28 = 7, 9 3) 7, 9 * 9, 2 = 72, 68 4) 72, 68 — 43, 78 = 28, 9.

Видео:Радиус и диаметрСкачать

Радиусы двух пересекающихся окружностей равны 17

ПРОПОРЦИОНАЛЬНЫЕ ЛИНИИ В КРУГЕ.

§ 11. Пропорциональные отрезки в круге.

1. Ферма моста ограничена дугой окружности (черт. 13); высота фермы MK= h = 3 м; радиус дуги АМВ пролёта R = 8,5 м. Вычислить длину АВ пролёта моста.

Черт. 13

2. В сводчатом подвале, имеющем форму полуцилиндра, надо поставить две стойки, каждую на одинаковом расстоянии от ближайшей стены. Определить высоту стоек, если ширина подвала по низу равна 4 м, а расстояние между стойками 2 м.

3. 1) Из точки окружности проведён перпендикуляр на диаметр. Определить его длину при следующей длине отрезков диаметра: 1) 12 см и3 см; 2) 16см и 9 см, 3)2 м и 5 дм.

2) Из точки диаметра проведён перпендикуляр до пересечения с окружностью. Определить длину этого перпендикуляра, если диаметр равен 40 см, а проведённый перпендикуляр отстоит от одного из концов диаметра на 8 см.

4. Диаметр разделён на отрезки: АС= 8 дм и СВ=5 м, и из точки С проведён к нему перпендикуляр CD данной длины. Указать положение точки D относительно круга, когда CD равняется: 1) 15 дм; 2) 2 м; 3) 23 дм.

5. АСВ—полуокружность; CD — перпендикуляр на диаметр АВ. Требуется:

1) определить DB, если AD = 25 и CD =10;

2) определить АВ, если AD: DB= 4 : 9 и CD=30;

3) определить AD, если CD=3AD, а радиус равен r;

4) определить AD, если AВ=50 и CD= 15.

6. 1) Перпендикуляр, опущенный из точки окружности на радиус, равный 34 см, делит его в отношении 8:9 (начиная от центра). Определить длину перпендикуляра.

2) Хорда BDC перпендикулярна к радиусу ODA. Определить ВС, если ОA = 25 см и AD=10 см.

3) Ширина кольца, образованного двумя концентрическими окружностями, равна 8 дм; хорда большей окружности, касательная к меньшей, равна 4 м. Определить радиусы окружностей.

7. С помощью сравнения отрезков доказать, что среднее арифметическое двух неравных чисел больше их среднего геометрического.

8. Построить отрезок, средний пропорциональный между отрезками 3 см и 5 см.

9. Построить отрезок, равный: √ 15 ; √ 10 ; √ 6 ; √ 3 .

10. ADB—диаметр; АС—хорда; CD—перпендикуляр к диаметру. Определить хорду АС: 1) если АВ=2 м и AD = 0,5 м; 2) если AD = 4 см и DB = 5 см; 3) если AB=20 м и DB= 15 м.

11. АВ—диаметр; АС—хорда; AD—её проекция на диаметр АВ. Требуется:

1) определить AD, если АB=18 см и АС=12 см;

2) определить радиус, если AС=12 м и AD=4 м;

3) определить DB, если AС=24 см и DB = 7 /₉ AD.

12. АВ—диаметр; АС—хорда; AD—её проекция на диаметр АВ. Требуется:

1) определить АС, если АВ = 35 см и AC=5AD;

2) определить АС, если радиус равен r и AC=DB.

13. Две хорды пересекаются внутри круга. Отрезки одной хорды равны 24 см и 14 см; один из отрезков другой хорды равен 28 см. Определить второй её отрезок.

14. Мостовая ферма ограничена дугой окружности (черт. 13); длина моста АВ= 6 м, высота А =1,2 м. Определить радиус дуги (OM= R).

Черт. 13

15. Два отрезка АВ и CD пересекаются в точке М так, что МА =7 см, MB=21 см,
МС = 3 см и MD = 16 см. Лежат ли точки А, В, С и D на одной окружности?

16. Длина маятника MA = l = 1 м (черт.14), высота подъёма его, при отклонении на угол α, CA = h= 10 см. Найти расстояние ВС точки В от МА (ВС = х).

Чет. 14.

17. Для перевода железнодорожного пути шириной b = 1,524 м в месте АВ (черт. 15) сделано закругление; при этом оказалось, ; что BС= а = 42,4 м. Определить радиус закругления OA = R.

Черт. 15.

18. Хорда АМВ повёрнута около точки М так, что отрезок МА увеличился в 2 1 /₂ раза. Как изменился отрезок MB?

19. 1) Из двух пересекающихся хорд одна разделилась на части в 48 см и 3 см, а другая — пополам. Определить длину второй хорды.

2) Из двух пересекающихся хорд одна разделилась на части в 12 м и 18 м, а другая— в отношении 3:8. Определить длину второй хорды.

20. Из двух пересекающихся хорд первая равна 32 см, а отрезки другой хорды равны
12 см и 16 см. Определить отрезки первой хорды.

21. Секущая ABC повёрнута около внешней точки А так, что внешний её отрезок АВ уменьшился в три раза. Как изменилась длина секущей?

22. Пусть ADB и AЕС—две прямые, пересекающие окружность: первая —в точках D и В, вторая —в точках E и С. Требуется:

1) определить АЕ, если AD = 5 см, DB=15 см и АС=25 см;

2)определитьBD, если АВ = 24 м, АС= 16 м и ЕС=10м;

3) определить АВ и АС, если АВ+АС=50 м, a AD : AE = 3:7.

23. Радиус окружности равен 7 см. Из точки, удалённой от центра на 9 см, проведена секущая так, что она делится окружностью пополам. Определить длину этой секущей.

24. МАВ и MCD—две секущие к одной окружности. Требуется:

1) определить CD, если МВ= 1 м, MD = 15 дм и CD = MA;

2) определить MD, если MA =18 см, АВ=12 см и MC:CD = 5:7;

3) определить АВ, если АВ= МС, МА = 20 и CD= 11.

25. Две хорды продолжены до взаимного пересечения. Определить длину полученных продолжений, если хорды равны а и b, а их продолжения относятся, как т : п.

26. Из одной точки проведены к окружности секущая и касательная. Определить длину касательной, если внешний и внутренний отрезки секущей соответственно выражаются следующими числами: 1) 4 и 5; 2) 2,25 и 1,75; 3) 1 и 2.

27. Касательная равна 20 см, а наибольшая секущая, проведённая из той же точки, равна 50 см. Определить радиус круга.

28. Секущая больше своего внешнего отрезка в 2 1 /₄ раза. Во сколько раз она больше касательной, проведённой из той же точки?

29. Общая хорда двух пересекающихся окружностей продолжена, и из точки, взятой на продолжении, проведены к ним касательные. Доказать, что они равны.

30. На одной стороне угла А отложены один за другим отрезки: AВ=6 см и ВС =8 см; а на другой стороне отложен отрезок AD = 10 см. Через точки В, С и D проведена окружность. Узнать, касается ли этой окружности прямая AD, а если нет, то будет ли точка D первой (считая от A) или второй точкой пересечения.

31. Пусть будет: АВ—касательная и ACD—секущая той же окружности. Требуется:

1) определить CD, если АВ = 2 см и AD = 4 см;

2) определить AD, если AC:CD = 4:5 и АВ=12 см;

3) определить АВ, если AB = CD и АС = а.

32. 1) Как далеко видно с воздушного шара (черт. 16), поднявшегося на высоту 4 км над землёй (радиус земли равен = 6370 км)?

Черт. 16. Черт. 17.

2) Гора Эльбрус (на Кавказе) поднимается над уровнем моря на 5 600 м. Как далеко можно видеть с вершины этой горы?

3) М — наблюдательный пункт высотой А метров над землёй (черт. 17); радиус земли R, МТ= d есть наибольшее видимое расстояние. Доказать, что d = √ 2Rh + h 2

Замечание. Так как h 2 вследствие своей малости сравнительно с 2Rh на результат почти не влияет, то можно пользоваться приближённой формулой d ≈ √ 2Rh .

33. 1) Касательная и секущая, выходящие из одной точки, соответственно равны 20 см и 40 см; секущая удалена от центра на 8 см. Определить радиус круга.

2) Определить расстояние от центра до той точки, из которой выходят касательная и секущая, если они соответственно равны 4 см и 8 см, а секущая удалена от центра на
12 см.

34. 1) Из общей точки проведены к окружности касательная и секущая. Определить длину касательной, если она на 5 см больше внешнего отрезка секущей и на столько же меньше внутреннего отрезка.

2) Из одной точки проведены к окружности секущая и касательная. Секущая равна а, а её внутренний отрезок больше внешнего отрезка на длину касательной. Определить касательную.

36. Из одной точки проведены к одной окружности касательная и секущая. Касательная больше внутреннего и внешнего отрезков секущей соответственно на 2 см и 4 см. Определить длину секущей.

36. Из одной точки проведены к окружности касательная и секущая. Определить их длину, если касательная на 20 см меньше внутреннего отрезка секущей и на 8 см больше внешнего отрезка.

37. 1) Из одной точки проведены к окружности секущая и касательная. Сумма их равна 30 см, а внутренний отрезок секущей на 2 см меньше касательной. Определить секущую и касательную.

2) Из одной точки проведены к окружности секущая и касательная. Сумма их равна 15 см, а внешний отрезок секущей на 2 см меньше касательной. Определить секущую и касательную.

38. Отрезок АВ продолжен на расстояние ВС. На АВ и АС, как на диаметрах, построены окружности. К отрезку АС в точке В проведён перпендикуляр BD до пересечения с большей окружностью. Из точки С проведена касательная СК к меньшей окружности. Доказать, что CD = СК.

39. К данной окружности проведены две параллельные касательные и третья касательная, пересекающая их. Радиус есть средняя пропорциональная между отрезками третьей касательной. Доказать.

40. Даны две параллельные прямые на расстоянии 15 дм одна от другой; между ними дана точка М на расстоянии 3 дм от одной из них. Через точку М проведена окружность, касательная к обеим параллелям. Определить расстояние между проекциями центра и точки М на одну из данных параллелей.

41. В круг радиуса r вписан равнобедренный треугольник, у которого сумма высоты и основания равна диаметру круга. Определить высоту.

42. Определить радиус круга, описанного около равнобедренного треугольника: 1) если основание равно 16 см, а высота 4 см; 2) если боковая сторона равна 12 дм, а высота 9 дм; 3) если боковая сторона равна 15 м, а основание 18 м.

43. В равнобедренном треугольнике основание равно 48 дм, а боковая сторона равна 30 дм. Определить радиусы кругов, описанного и вписанного, и расстояние между их центрами.

44. Радиус равен r, хорда данной дуги равна а. Определить хорду удвоенной дуги.

45. Радиус окружности равен 8 дм; хорда АВ равна 12 дм. Через точку А проведена касательная, а из точки В—хорда ВС, параллельная касательной. Определить расстояние между касательной и хордой ВС.

46. Точка А удалена от прямой MN на расстояние с. Данным радиусом r описана окружность так, что она проходит через точку А и касается линии MN. Определить расстояние между полученной точкой касания и данной точкой А.

🌟 Видео

Теорема о числе точек пересечения двух окружностейСкачать

Общая хорда двух окружностейСкачать

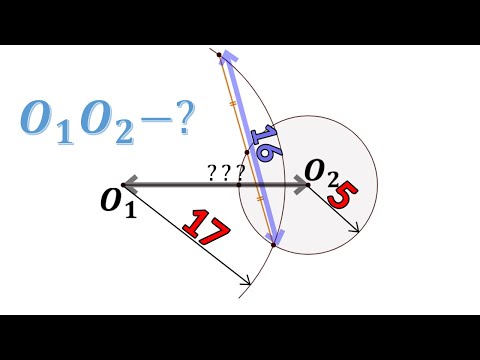
Сможешь найти расстояние между центрами пересекающихся окружностей?Скачать

10.17.1. Планиметрия. Гордин Р.К.Скачать