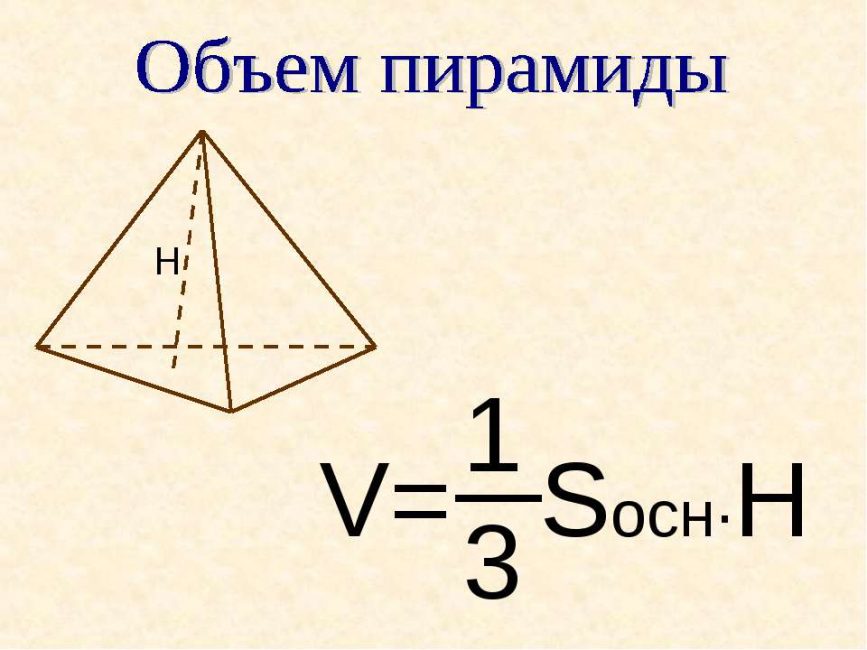
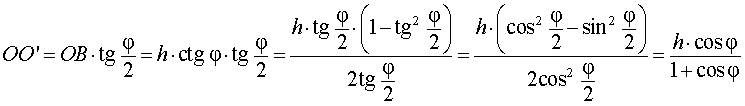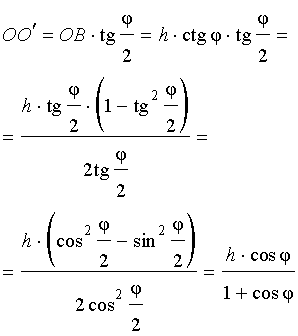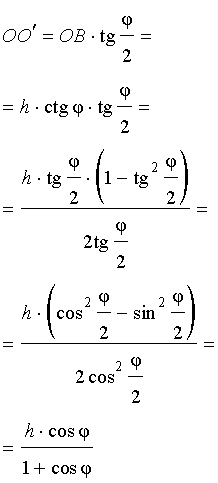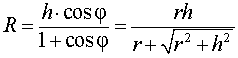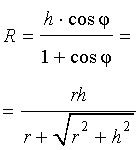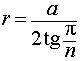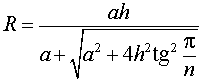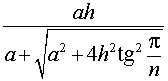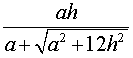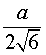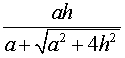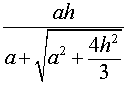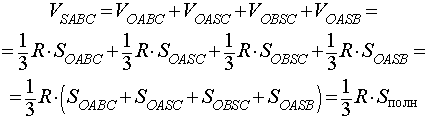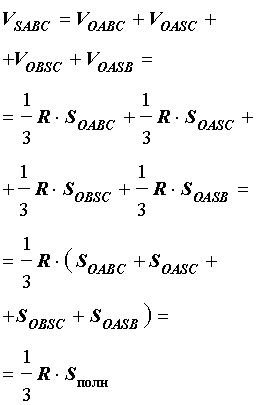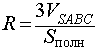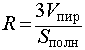Как найти высоту пирамиды через радиус вписанной окружности (3 видео)

Как найти высоту в пирамиде: треугольной, четырехугольной, правильной

Высота основания в пирамиде – тема, на которую часто попадаются задачи на экзаменах и в старших классах. Решать такие задачи просто, если понимать принцип решения и знать формулы.

В нашей статье, вы без лишних формул и теории сможете понять, как решать задачи на нахождение высоты в пирамиде. Обратите внимание, что в разделе «формулы» отсутствуют все формулы правильной пирамиды, так как наша цель – научить решать задачи на нахождение высоты.

Содержание этой статьи:

Содержание

Теория
Правильная пирамида
Основные свойства
Четырехугольная пирамида
Треугольная пирамида
Необходимые знания для нахождения высоты
Формулы для нахождения высоты
ВИДЕО: Примеры решения задач
Нахождение высоты в правильной пирамиде
Треугольная пирамида
Четырехугольная пирамида
Часто задаваемые вопросы
Типичные ошибки на ЕГЭ
Полезные советы
Пирамида. Правильная пирамида
Сфера, вписанная в пирамиду
Биссекторная плоскость. Основное свойство биссекторной плоскости
Сфера, вписанная в пирамиду. Свойства пирамиды, описанной около сферы
Радиус сферы, вписанной в правильную n — угольную пирамиду
Сфера, вписанная в треугольную пирамиду. Формула для радиуса вписанной сферы
🌟 Видео

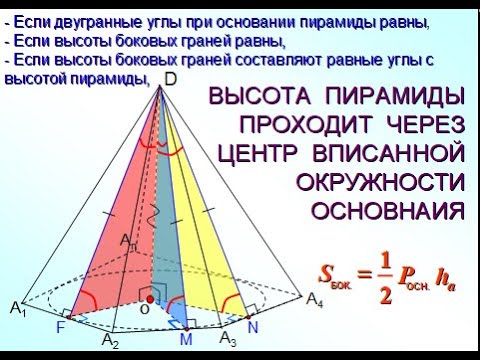
Видео:Пирамиды, в которых высота проходит через центр вписанной в основание окружностиСкачать

Теория

Правильная пирамида

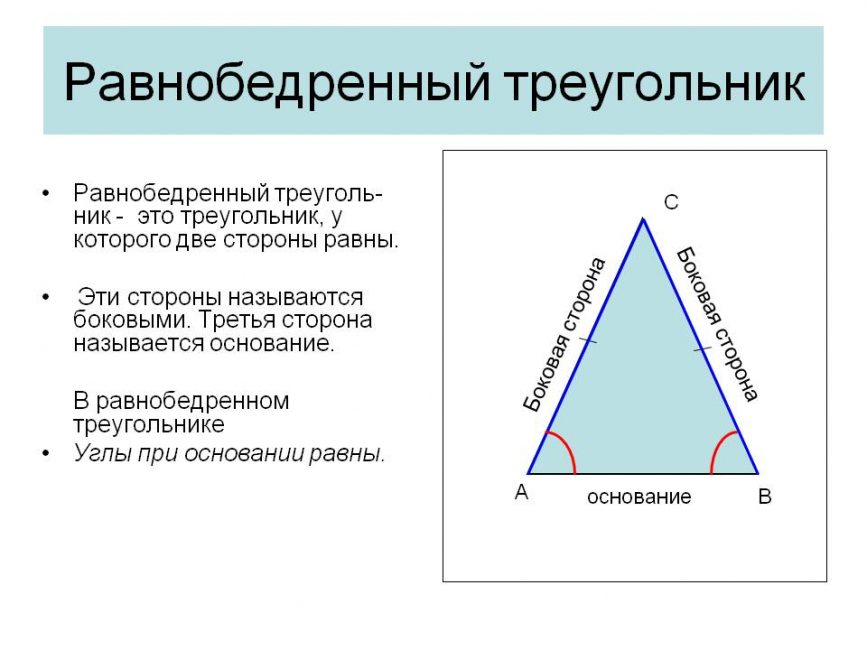
Правильная пирамида имеет в основании многоугольник, а высота проходит через центр основания. Боковые грани – равнобедренные треугольники. Напомним, что в равнобедренном треугольнике две стороны равны, следовательно, боковые ребра в правильной пирамиде тоже равны. Многоугольник в основании правильный, т.е. его стороны равны.

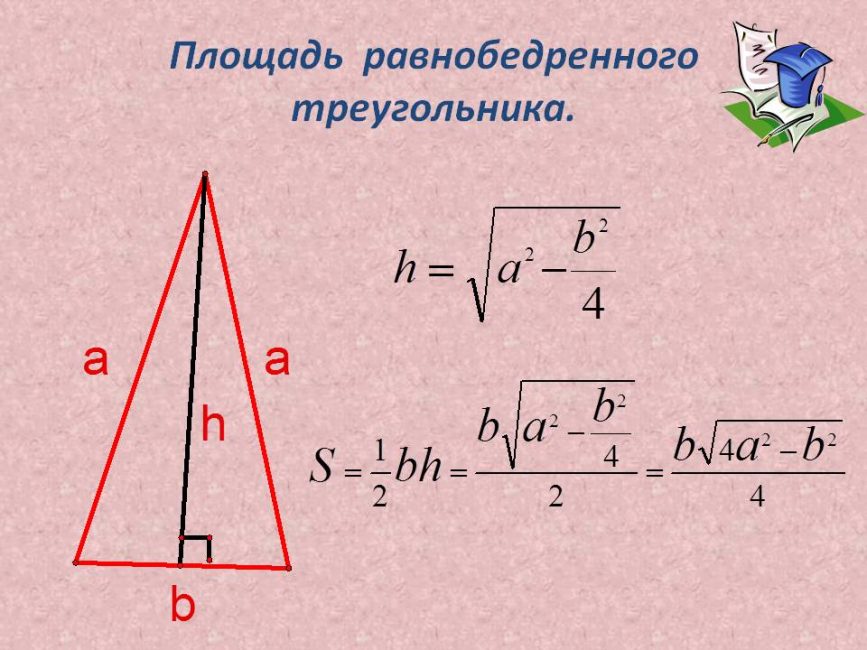
Для решения задач понадобится знать теоремы равнобедренного треугольника:

Основные свойства

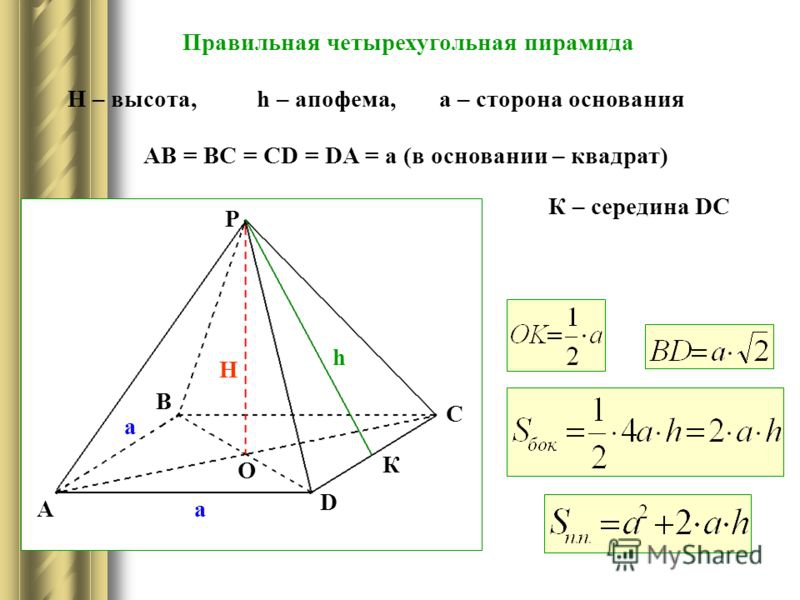
Четырехугольная пирамида

В основании – многоугольник; остальные грани – треугольники, соединяющиеся в общей вершине.

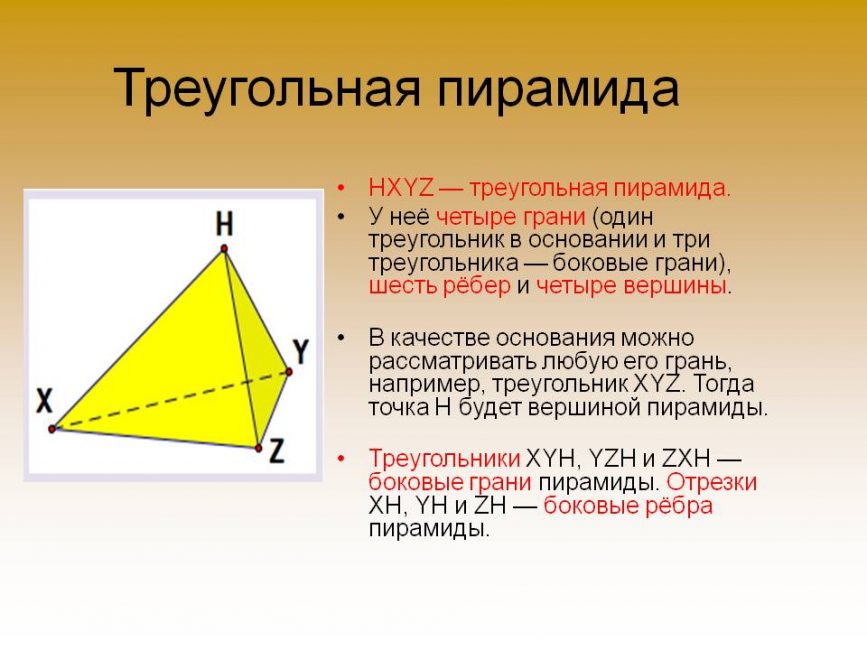
Треугольная пирамида

В качестве основания можно рассматривать любую грань. Вся фигура состоит из треугольников.

Необходимые знания для нахождения высоты

Когда теория закреплена, можно переходить к формулам.

Формулы для нахождения высоты

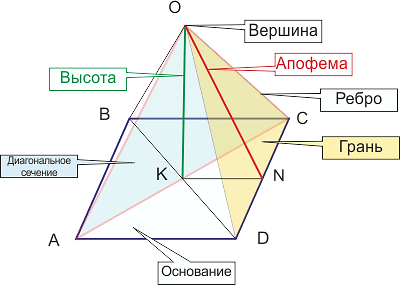
Запомните, что маленькая буква h – это апофема, а большая H – высота.

В некоторых задачах, высоту можно найти через объем:

ВИДЕО: Примеры решения задач

Нахождение высоты в правильной пирамиде

Ниже будут представлены текстовые решения часто встречающихся задач.

Треугольная пирамида

Задача 1

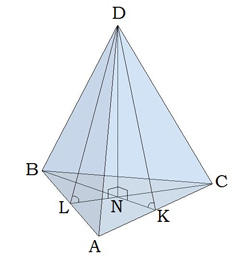
В правильной треугольной пирамиде DBAC с вершиной D биссектрисы треугольника BAC пересекаются в точке N. Площадь треугольника BAC равна 4; объем пирамиды равен 12. Найдите длину отрезка DN.

DN – высота, следовательно, объем фигуры можно выразить по формуле:

DN = 3V/S основания = 3*12/4 = 9

Задача 2

DBAC – медианы основания BAC. Они пересекаются в точке N. Площадь ΔBAC равна 18, V = 20; найдите высоту.

Пользуясь формулой объема, получается:

DN = 3V/S ΔBAC = 3*36/18 = 108/18 = 6

Четырехугольная пирамида

Задача 1

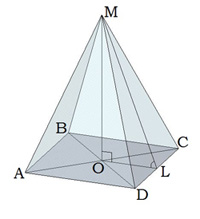
Найдите высоту пирамиды, если ML = 10, а DC = 12. В основании квадрат.

ML – это апофема, сторона нам известна, следовательно, можно применить формулу для нахождения OL:

Известно, что MOL – прямоугольный угол. Применим теорему Пифагора:

MO ² = √ML ² — √OL ² = √100- √36 = √64

Задача 2

Известно, что диагональ AC = 20, ML = 10, а сторона DC = 12; найдите MO правильной четырехугольной пирамиды.

Найдем OL

В основании фигуры – квадрат, стороны и углы которого равны. Значит, половина диагонали = 10. Рассмотрим треугольник LOC, он – прямоугольный. Из исходных данный ясно, что LC = 6 (в равнобедренном треугольнике, высота, проведенная из вершины, делит основание на 2 равные части – это свойство р/б треугольника).

Пользуясь теоремой Пифагора, находим OL:

OL² = √OC² — √LC² = √100 – √36 = √64 = 8

Задача 3

Ищем MO

Пользуясь той же теоремой, находим высоту:

MO² = √ML² – √OL² = 100 – 64 = 36

Задача 4

Известно, что в основании ABCD, AB=CD=BC=AD. Треугольник DMC имеет площадь 36см, DC = 4, OL = 6. Определите тип фигуры и найдите высоту.

Исходя из информации про основание, мы сделали вывод, что перед нами правильная пирамида – стороны основания равны. Следовательно, перед нами четырехугольная правильная пирамида.

Из первого вывода следует, что боковые грани – равнобедренные треугольники, а высота и медиана этих треугольников – апофема. Пользуясь формулами, найдем высоту.

Площадь равнобедренного треугольника

Теперь у нас есть апофема, а OL нам было уже давно. MOL – прямоугольный треугольник, 2 стороны которого, мы уже знаем. Следовательно, мы можем посчитать высоту.

MO = ML – OL = 18 – 6 = 12

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Часто задаваемые вопросы

Часто в задании не указывают какой тип фигуры, чтобы человек сам догадался и применил нужные формулы. Понять какой тип фигуры легко – начните решение задачи с рассмотрения основания и заучивания свойств фигуры.

Зная определения и свойства, определить тип фигуры очень легко.

Чтобы решать задачи, человек должен включать логику, а не подставлять исходные числа в знакомые формулы. С этим расчетом, в некоторых задачах умышленно добавляют лишние данные, которые могут даже не использоваться при решении. Чаще такое встречается в задачах на ЕГЭ.

Для удобства, человек может не выделять отдельно высоту, а сразу писать, например, BE (если B – вершина, а E – основание). То же с апофемой. Важно, чтобы сам человек осознавал, что это за линия и как ее использовать в решении.

Ключ к пониманию стереометрии – умение визуализировать объекты в пространстве. Если в дополнение к этому умению, знать формулы, свойства и теорию – задачи будут решаться быстро и безошибочно.

Если выразить высоту через формулу объема, то получится следующее:

Пример: объем пирамиды равен 70 куб. см., а площадь боковых граней – 30см²

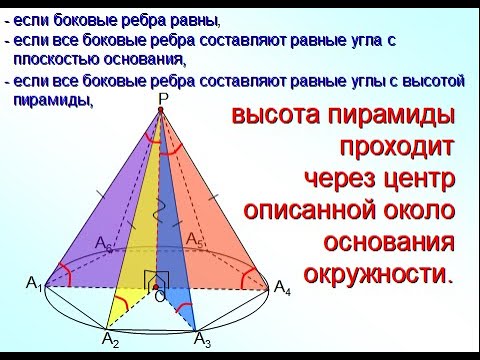
Видео:Пирамиды, в которых высота проходит через центр описанной около основания окружностиСкачать

Типичные ошибки на ЕГЭ

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Полезные советы

Если в задаче указан объем – ищите высоту через него.
Делите равнобедренные треугольники на прямоугольные – так быстрее и проще решить задачу.
Учите квадратные корни чисел – так, вы будете быстрее справляться с теоремой Пифагора.
Не кидайтесь сразу к решению – изучите исходные данные и сделайте правильные выводы.
Если в заданиях получаются слишком крупные числа (от 1000), то перепроверьте решение – вероятно, вы допустили ошибку. В заданиях в учебнике и на экзамене практически не используются крупные числа.

Чтобы успешно решить задачу для нахождения высоты пирамиды, достаточно знать теорию и формулы. Добавив к своим знаниям немного практики и внимательности, вы легко и быстро будете решать подобные задачи! Если вы не согласны с рейтингом статьи, то просто поставьте свои оценки и аргументируйте их в комментариях. Ваше мнение очень важно для наших читателей. Спасибо!

Видео:10 класс, 33 урок, Правильная пирамидаСкачать

Пирамида. Правильная пирамида

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Данный видеоурок поможет пользователям получить представление о теме Пирамида. Правильная пирамида. На этом занятии мы познакомимся с понятием пирамиды, дадим ей определение. Рассмотрим, что такое правильная пирамида и какими свойствами она обладает. Затем докажем теорему о боковой поверхности правильной пирамиды.

Видео:Задача 6 №27926 ЕГЭ по математике. Урок 141Скачать

Сфера, вписанная в пирамиду

Как найти высоту пирамиды через радиус вписанной окружности

Биссекторная плоскость. Основное свойство биссекторной плоскости

Сфера, вписанная в пирамиду. Свойства пирамиды, описанной около сферы

Радиус сферы, вписанной в правильную n — угольную пирамиду

Сфера, вписанная в треугольную пирамиду. Формула для радиуса вписанной сферы

Видео:Найти высоту Пирамиды Д430Скачать

Биссекторная плоскость. Основное свойство биссекторной плоскости

Определение 1. Биссекторной плоскостью двугранного угла называют такую плоскость, которая проходит через ребро двугранного угла и делит этот угол на два равных двугранных угла (рис. 1).

Утверждение 1. Точка, расположенная внутри двугранного угла, находится на одном и том же расстоянии от граней этого угла тогда и только тогда, когда она лежит на биссекторной плоскости.

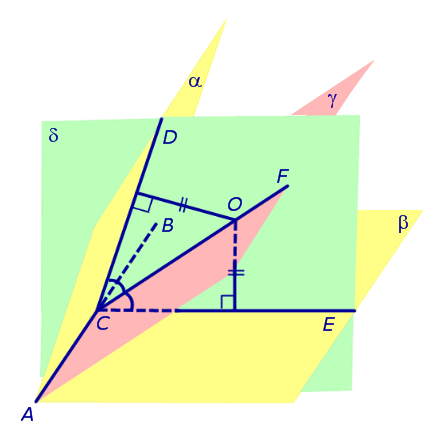
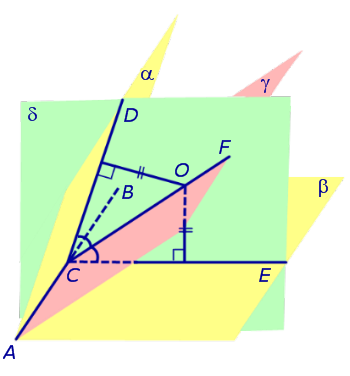
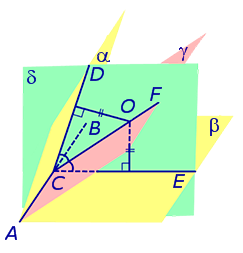
Доказательство. Рассмотрим произвольную точку O, расположенную внутри двугранного угла, и проведем через эту точку плоскость δ , перпендикулярную к ребру AB двугранного угла (рис. 2).

Плоскость δ пересекает ребро AB двугранного угла в точке C, а грани двугранного угла α и β по лучам CD и CE соответственно. Угол DCE является линейным углом двугранного угла. Биссекторная плоскость γ пересекает плоскость δ по биссектрисе CF линейного угла DCE .

Таким образом, справедливость утверждения вытекает из соответствующих теорем о свойствах биссектрисы угла. Доказано.

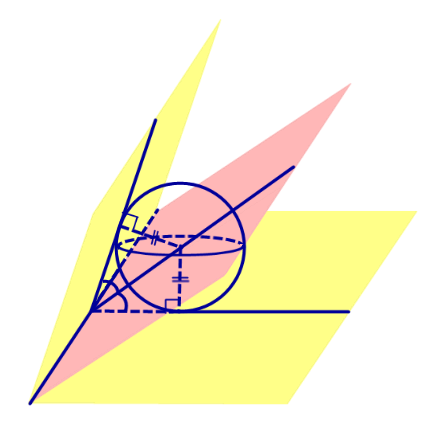
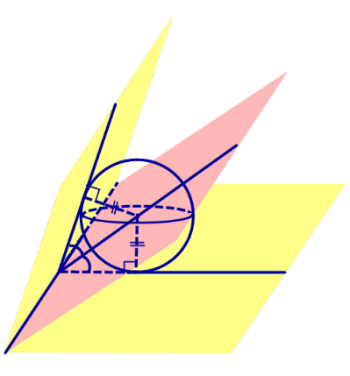
Следствие 1. Если сфера, расположенная внутри двугранного угла, касается каждой из плоскостей граней этого угла, то центр сферы находится на биссекторной плоскости двугранного угла (рис. 3).

Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Сфера, вписанная в пирамиду. Свойства пирамиды, описанной около сферы

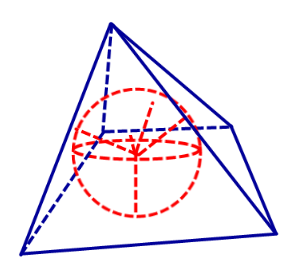
Определение 2. Сферой, вписанной в пирамиду, называют такую сферу, которая касается плоскостей всех граней пирамиды, причем точки касания лежат на гранях пирамиды (рис. 4).

Определение 3. Если сфера вписана в пирамиду, то пирамиду называют описанной около сферы.

Если сфера вписана в пирамиду, то она касается граней каждого внутреннего двугранного угла, образованного соседними гранями пирамиды. В соответствии со следствием 1 центр вписанной в пирамиду сферы должен находиться в точке пересечения биссекторных плоскостей всех внутренних двугранных углов, образованных соседними гранями пирамиды.

Если у пирамиды нет точки, в которой пересекаются биссекторные плоскости всех внутренних двугранных углов, образованных соседними гранями пирамиды, то в такую пирамиду нельзя вписать сферу.

Замечание 1. Для того, чтобы проверить, можно ли в пирамиду вписать сферу, достаточно проверить, существует ли точка пересения биссекторных плоскостей всех внутренних двугранных углов при основании пирамиды. Если такая точка существует, то она будет равноудалена как от основания пирамиды, так и от каждой из боковых граней.

Рассмотрим несколько типов пирамид, в которые можно вписать сферу.

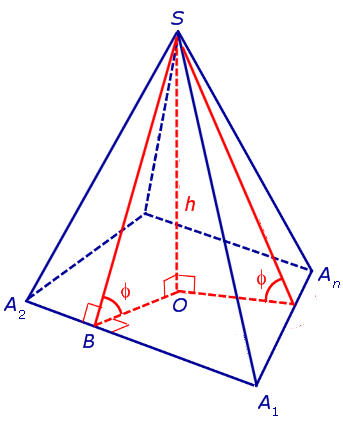
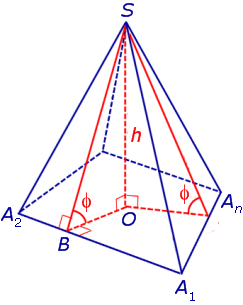
Утверждение 2. Если у пирамиды SA₁A₂ . A_n основание O перпендикуляра, опущенного из вершины S на плоскость основания пирамиды, лежит внутри многоугольника A₁A₂ . A_n , а все боковые грани пирамиды наклонены под одним и тем же углом к плоскости основания пирамиды, то в такую пирамиду можно вписать сферу.

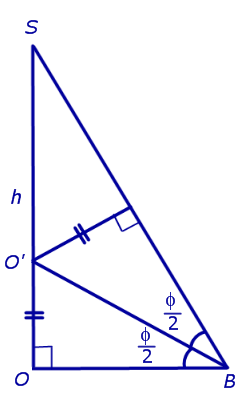
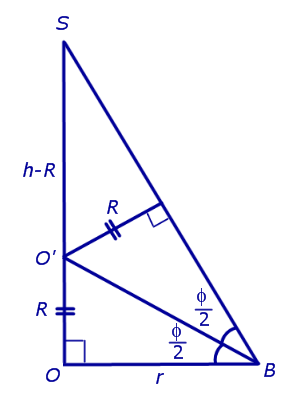
Доказательство. Пусть все боковые грани пирамиды наклонены к плоскости основания под углом φ , а высота пирамиды равна h. Рассмотрим, например, боковую грань SA₁A₂ и проведем в ней высоту SB (рис. 5).

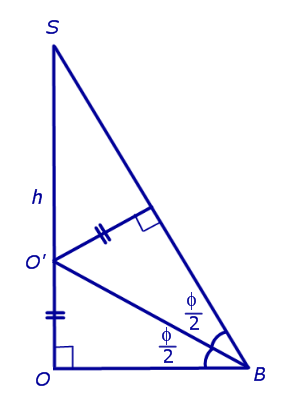
По теореме о трех перпендикулярах отрезок OB перпендикулярен ребру A₁A₂ . Следовательно, угол SBO является линейным углом двугранного угла между боковой гранью SA₁A₂ и плоскостью основания пирамиды и равен φ. Биссекторная плоскость этого двугранного угла пересекает высоту пирамиды в точке O’ (рис. 6).

Катет OB прямоугольного треугольника SOB выражается через высоту пирамиды h и угол φ по формуле

Катет OO’ прямоугольного треугольника OO’B выражается через высоту пирамиды h и угол φ по формуле

Поскольку длина отрезка OO’ не зависит от выбора боковой грани пирамиды, то биссекторные плоскости всех внутренних двугранных углов при основании пирамиды пересекаются в точке O’, которая и является центром вписанной в пирамиду сферы.

Доказательство утверждения 2 завершено.

Поскольку у любой правильной пирамиды все внутренние двугранные углы при основании равны, то справедливо

Следствие 2. В любую правильную пирамиду можно вписать сферу, причем ее радиус R выражается через высоту пирамиды h и внутренний двугранный угол при основании пирамиды φ по формуле

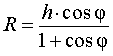(1)

Видео:Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать

Радиус сферы, вписанной в правильную n — угольную пирамиду

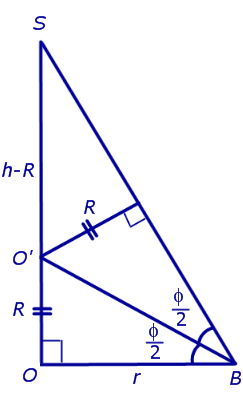
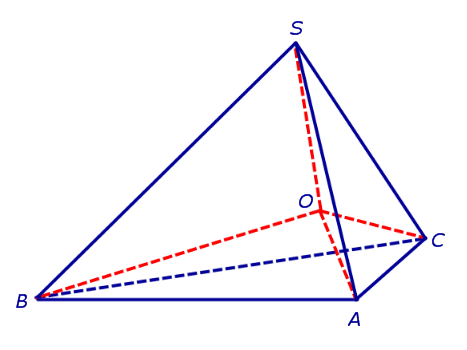
Решение. Рассмотрим правильную n — угольную пирамиду SA₁A₂ . A_n и обозначим символом O’ центр вписанной в пирамиду сферы, а буквой O – центр основания пирамиды. Проведем плоскость через высоту пирамиды SO и апофему SB какой-либо боковой грани (рис. 7).

Буквой R на рисунке 7 обозначен радиус вписанной в пирамиду сферы, буквой r – радиус вписанной в основание пирамиды окружности, а буквой φ – внутренний двугранный угол при основании пирамиды. Из прямоугольного треугольника OSB получаем

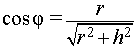(2)

В силу следствия 2 из формул (1) и (2) получаем

из формулы (3) получаем соотношение

Ответ.

Следствие 3. Радиус сферы, вписанной в правильную треугольную пирамиду с высотой h и ребром основания a, равен

Следствие 4. Радиус сферы, вписанной в правильный тетраэдр с ребром a, равен

Следствие 5. Радиус сферы, вписанной в правильную четырехугольную пирамиду с высотой h и ребром основания a, равен

Следствие 6. Радиус сферы, вписанной в правильную шестиугольную пирамиду с высотой h и ребром основания a, равен

Видео:Вычисление радиуса сферы, вписанной в правильную треугольную пирамидуСкачать

Сфера, вписанная в треугольную пирамиду.
Формула для радиуса вписанной сферы

Утверждение 3. В любую треугольную пирамиду можно вписать сферу.

Доказательство. Доказательство этого утверждения напоминает планиметрическое доказательство возможности вписать окружность в произвольный треугольник.

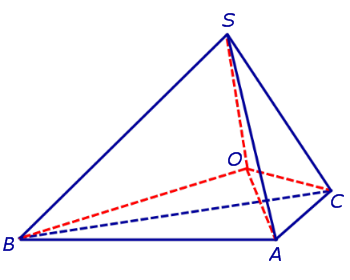
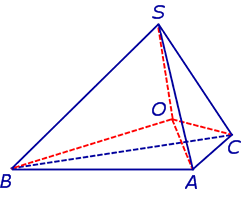
Действительно, пусть SABC – произвольный тетраэдр. Биссекторная плоскость внутреннего двугранного угла с ребром AC и биссекторная плоскость внутреннего двугранного угла с ребром AB пересекаются по некоторой прямой, проходящей через вершину A. Биссекторная плоскость внутреннего двугранного угла в ребром BC пересекает эту прямую в единственной точке O , которая и является центром вписанной сферы (рис. 8).

Получим формулу, позволяющую вычислить радиус вписанной в тетраэдр SABC сферы. Для этого заметим, что объем пирамиды SABC равен сумме объемов пирамид OABC, OSCA, OSAB, OSCB, причем высота каждой из пирамид OABC, OSCA, OSAB, OSCB равна радиусу R вписанной в пирамиду SABC сферы. Если обозначить площади граней тетраэдра SABC символами

а объемы пирамид SABC, OABC, OSCA, OSAB, OSCB – символами

то справедливы следующие равенства:

где символом S_полн обозначена площадь полной поверхности пирамиды SABC.

Замечание 2. Если в пирамиду (необязательно треугольную) можно вписать сферу, то, рассуждая аналогично, можно получить следующую формулу для радиуса вписанной в пирамиду сферы