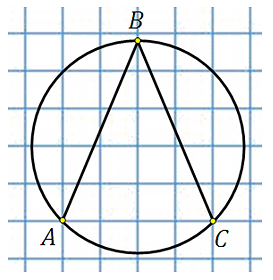
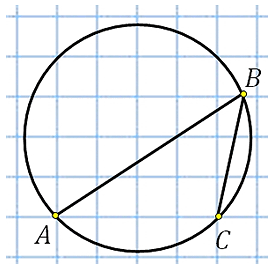
27887. Найдите величину угла ABC. Ответ дайте в градусах.
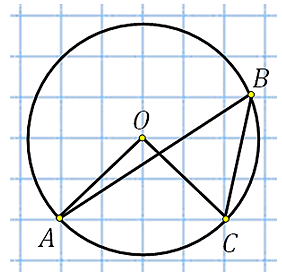
Отметим центр окружности. Обозначим его точкой О, построим центральный угол АОС:
Угол АОС равен 90 0 . Это видно по тому как проходят АО и ОС относительно клетчатой сетки. Угол АВС это вписанный угол, построенный на той же дуге.
По свойству вписанного угла:
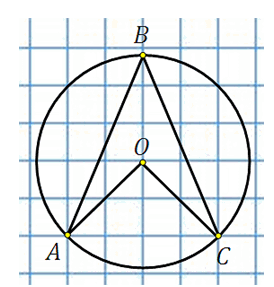
27888. Найдите величину угла ABC. Ответ дайте в градусах.
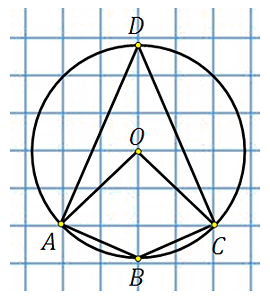
Отметим центр окружности. Обозначим его точкой О, построим центральный угол АОС и вписанный угол ADC:
Центральный угол АОС равен 90 0 . По свойству вписанного угла
Известно, что у четырёхугольника вписанного в окружность сумма противоположных углов равна 180 градусам, следовательно:
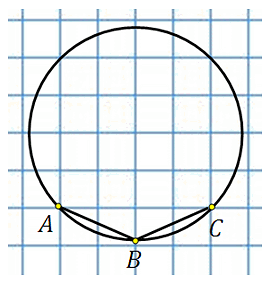
27889. Найдите величину угла ABC. Ответ дайте в градусах.
Отметим центр окружности (видно о клетчатой сетке). Обозначим его точкой О, построим центральный угол АОС:
Угол АОС равен 90 градусов. Угол АВС это вписанный угол, построенный на той же дуге. По свойству вписанного угла:
Видео:№68. На рисунке 48 ∠AOB = 50°, ∠FOE = 70°. Найдите углы АОС, BOD, СОЕ и COD.Скачать

Найдите угол вас изображенный на рисунке окружность
На окружности отмечены точки A и B так, что меньшая дуга AB равна 72°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 72°. Треугольник AOB — равнобедренный. Значит,
Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 54° = 36°.
Читатели, знакомые с теоремой «Угол между хордой и касательной равен половине дуги, стягиваемой хордой», могут решить эту задачу в одно действие: ∠ABC = 72° : 2 = 36°.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 56°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 56°. Треугольник AOB — равнобедренный. Значит,
Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 62° = 28°.
Читатель, знающий правило «Угол между хордой и касательной равен половине дуги, стягиваемой хордой», может решить эту задачу в одно действие:
Найдите угол ABC. Ответ дайте в градусах.
Впишем в окружность квадрат так, как показано на рисунке. Стороны квадрата отсекают на окружности равные дуги. Поэтому градусная мера дуги AC, на которую опирается угол ABC, составляет полного угла 360°, т. е. равна 270°. Угол ABC вписанный, поэтому он равен половине дуги, на которую опирается. Следовательно, угол ABC равен 135°.
Видео:Найдите угол: задача по геометрииСкачать

Геометрия. Урок 1. Задания. Часть 2.
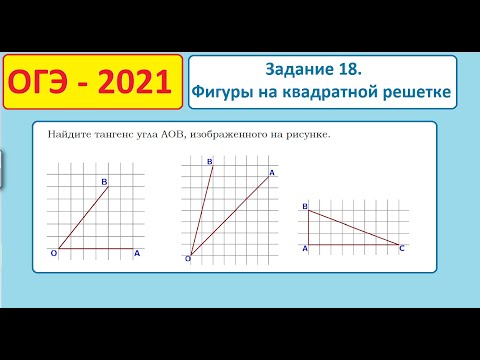
№8. Найдите тангенс угла A O B , изображенного на рисунке.
Решение:
Опустим перпендикуляр A H на сторону O B .
Рассмотрим прямоугольный △ A O H :
Тангенс угла – отношение противолежащего катета к прилежащему.
tg ∠ A O H = A H O H = 4 2 = 2
№9. Найдите тангенс угла A треугольника A B C б изображённого на рисунке.
Решение:
Тангенс угла – это отношение противолежащего катета к прилежащему.
tg ∠ B A C = B C A C = 2 5 = 0,4
№10. На рисунке изображена трапеция A B C D . Используя рисунок, найдите sin ∠ B A H .
Решение:
Рассмотрим прямоугольный △ A B H :
Синус угла – отношение противолежащего катета к гипотенузе.
sin ∠ A = B H A B
Найдем A B по теореме Пифагора:
A B 2 = A H 2 + B H 2
A B 2 = 3 2 + 4 2
A B 2 = 9 + 16 = 25
A B = ± 25 = [ − 5 не подходит 5 подходит
sin ∠ A = B H A B = 4 5 = 0,8
№11. На рисунке изображен ромб A B C D . Используя рисунок, найдите tg ∠ O B C .
Решение:
Тангенс угла – это отношение противолежащего катета к прилежащему.
tg ∠ O B C = O C B O = 3 4 = 0,75
№12. На рисунке изображена трапеция A B C D . Используя рисунок, найдите cos ∠ H B A .
Решение:
Рассмотрим прямоугольный △ A B H :
Косинус угла – отношение прилежащего катета к гипотенузе.
cos ∠ A B H = B H A B
Найдем A B по теореме Пифагора:
A B 2 = A H 2 + B H 2
A B 2 = 6 2 + 8 2
A B 2 = 36 + 64 = 100
A B = ± 100 = [ − 10 не подходит 10 подходит
cos ∠ A B H = B H A B = 8 10 = 0,8
№13. Найдите тангенс угла, изображенного на рисунке.
Решение:
tg β = tg ( 180 ° − α ) = − tg α
Рассмотрим прямоугольный △ B C H .
Тангенс угла – отношение противолежащего катета к прилежащему.
tg α = C H B H = 3 1
tg β = − tg α = − 3
№14. Найдите тангенс угла A O B .
Решение:
Опустим высоту B H на сторону O A .
Рассмотрим прямоугольный △ O B H :
Найдем B H и O H по теореме Пифагора:
B H 2 = 2 2 + 8 2 = = 4 + 64 = 68
B H = ± 68 = ± 4 ⋅ 17 = ± 4 ⋅ 17 = ± 2 17 = [ − 2 17 не подходит 2 17 подходит
O H 2 = 1 2 + 4 2 = 1 + 16 = 17
O H = ± 17 = [ − 17 не подходит 17 подходит
📸 Видео
№66. На рисунке 41 найдите углы 1, 2, 3, 4, если: a) ∠2 +∠4 = 220°; б) 3(∠1 +∠3) = ∠Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Демоверсия ОГЭ 2022. Математика. ГЕОМЕТРИЯ 1 частьСкачать

ОГЭ как найти тангенс угла, если нет треугольника #математика #огэ #огэматематика #геометрияСкачать

Найдите угол ABC. Ответ дайте в градусах. | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

Найдите угол: задача по геометрииСкачать

ОГЭ математика ФИГУРЫ НА РЕШЕТКЕ 19#1🔴Скачать

ОГЭ 2021. Задание 18. Фигуры на квадратной решеткеСкачать
Геометрия Используя данные рисунка найдите отрезок AD если CD = a угол BAC = γ угол DBA = βСкачать

Найдите угол: задача по геометрииСкачать

№51. На рисунке 38 угол AOD— прямой, ∠AOB = = ∠BOC = Z∠COD. Найдите угол, образованныйСкачать
Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Математика ОГЭ 2020. Углы. Задание 16№ 311412 (1)Скачать

#2_Самое сложное задание 16 ОГЭ 2021. Задачи по геометрии. Вписанные и центральные углы.Скачать

ОГЭ 2021. Фигуры на квадратной решетке.Скачать
Точка O – центр окружности, ∠BOC=160° ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

№112. На рисунке 66 АВ = ВС, ∠1=130°. Найдите ∠2.Скачать

ОГЭ по математике. Треугольник вписан в окружность . (Вар. 4) √ 17 модуль геометрия ОГЭСкачать