Радиус вписанной окружности в трапеции равен 30 найдите высоту

Видео:Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать

Ваш ответ

Видео:Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

решение вопроса

Видео:Задание 16 ОГЭ по математике. Окружность вписана в трапецию.Скачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,044
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать

Трапеция. Свойства трапеции

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .

Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .

Видео:Геометрия, номера 45.1, 46.1 (радиус вписанной окружности)Скачать

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия –

Отношение площадей этих треугольников есть .

4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Видео:Задача 6 №27926 ЕГЭ по математике. Урок 141Скачать

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Вписанная окружность

Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то

Видео:Радиус описанной окружности трапецииСкачать

Площадь

или где – средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

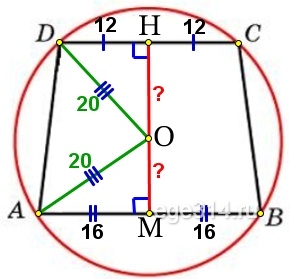
Решение №2085 Основания равнобедренной трапеции равны 32 и 24. Радиус описанной окружности равен 20. Центр окружности лежит внутри трапеции. Найдите высоту трапеции.

Основания равнобедренной трапеции равны 32 и 24. Радиус описанной окружности равен 20. Центр окружности лежит внутри трапеции. Найдите высоту трапеции.

Через центр окружности О проведём высоту НМ, она делит основания равнобедренной трапеции пополам:

DH = DC/2 = 24/2 = 12
АМ = АВ/2 = 32/2 = 16

Проведём радиусы DO и АО, получаем два прямоугольных треугольника ΔDHO и ΔAMO, найдём в них по теореме Пифагора катеты HO и МО соответственно:

Найдём высоту трапеции НМ:

НМ = НО + МО = 16 + 12 = 28

📸 Видео

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту треугольникаСкачать

ЕГЭ математика 2023 Вариант 2 задача 1Скачать

Задача про трапецию, описанную около окружностиСкачать

Нафиг теорему синусов 3 задание проф. ЕГЭ по математике (часть II)Скачать

ОГЭ2021. Трапеция описана около окружности. #shortsСкачать

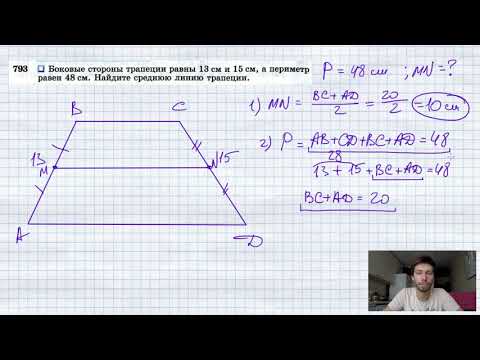
№793. Боковые стороны трапеции равны 13 см и 15 см, а периметр равен 48 см. Найдите среднюю линиюСкачать

2111 основания равнобедренной трапеции равны 8 и 6Скачать

Трапеция вписана в окружность. Найти радиус окружностиСкачать

8 класс, 6 урок, ТрапецияСкачать

2104 Найдите высоту трапеции в которую вписана окружность радиуса 28Скачать