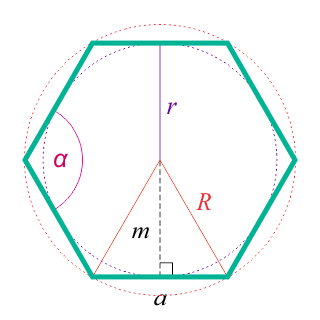
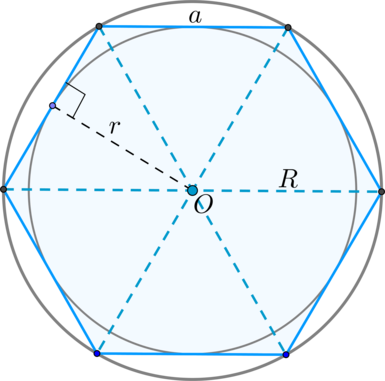
Деление шестиугольника на треугольники (7 видео)

Гексагон

Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.

Шестиугольник — это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.

Выпуклый шестиугольник — это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.

Правильный шестиугольник — это шестиугольник, все стороны которого равны между собой.

Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 — 2 ) = 720 градусов.

При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.

Содержание

Свойства правильного шестиугольника
Правильный шестиугольник и его свойства
Шестиугольники на решетке
Задача
Подсказка
Решение
Послесловие
Доказательство
Решение головоломки
🌟 Видео

Свойства правильного шестиугольника

все внутренние углы равны между собой
каждый внутренний угол правильного шестиугольника равен 120 градусам
все стороны равны между собой
сторона правильного шестиугольника равна радиусу описанной окружности
большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
меньшая диагональ правильного шестиугольника в ( sqrt ) раз больше его стороны.
vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
правильный шестиугольник заполняет плоскость без пробелов и наложений
диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности. 6.
инвариантен относительно поворота плоскости на угол, кратный относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями)
nреугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60° .

Внутренние углы Внутренние углы в правильном шестиугольнике равны (120^circ) :

Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)

Радиус вписанной окружности правильного шестиугольника равен апофеме:

(r = m = alargefrac<>normalsize)

Радиус описанной окружности равен стороне правильного шестиугольника:

Периметр правильного шестиугольника

Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны

(S = pr = largefrac<>normalsize),
где (p) − полупериметр шестиугольника.

Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности

Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

Видео:Сумма углов треугольника. Геометрия 7 класс | Математика Скачать

Правильный шестиугольник и его свойства

Определение

Выпуклый многоугольник называется правильным, если все его стороны равны и все его углы равны.

Замечание

Т.к. сумма всех углов (n) –угольника равна (180^circ(n-2)) , то каждый угол правильного (n) –угольника равен [alpha_n=dfracn cdot 180^circ]

Пример

Каждый угол правильного четырехугольника (т.е. квадрата) равен (dfrac 4cdot 180^circ=90^circ) ;

каждый угол правильного шестиугольника равен (dfrac6cdot 180^circ=120^circ) .

Теоремы

1. Около любого правильного многоугольника можно описать окружность, и притом только одну.

2. В любой правильный многоугольник можно вписать окружность, и притом только одну.

Следствия

1. Окружность, вписанная в правильный многоугольник, касается всех его сторон в серединах.

2. Центры вписанной и описанной окружности у правильного многоугольника совпадают.

Теорема

Если (a) – сторона правильного (n) –угольника, (R) и (r) – радиусы описанной и вписанной окружностей соответственно, то верны следующие формулы: [begin S&=dfrac n2ar\ a&=2Rcdot sindfracn\ r&=Rcdot cosdfracn end]

Свойства правильного шестиугольника

1. Сторона равна радиусу описанной окружности: (a=R) .

2. Радиус описанной окружности является биссектрисой угла правильного шестиугольника.

3. Все углы правильного шестиугольника равны (120^circ) .

4. Площадь правильного шестиугольника со стороной (a) равна (dfrac<3sqrt>a^2) .

5. Диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу (r) вписанной в правильный шестиугольник окружности.

6. Инвариантен относительно поворота плоскости на угол, кратный (60^circ) относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями).

Замечание

В общем случае правильный (n) -угольник инвариантен относительно поворота на угол (dfrac) .

Видео:2 2 2 изометрия треугольника и шестиугольникаСкачать

Шестиугольники на решетке

Видео:Свойства правильного шестиугольникаСкачать

Задача

Правильный шестиугольник со стороной n разбит на единичные треугольники. Отметим все вершины этих треугольников. Найдите:
а) количество правильных шестиугольников с вершинами в отмеченных точках, стороны которых лежат на линиях разбиения (как оранжевый шестиугольник на рис. 1);
б) количество всех правильных шестиугольников с вершинами в отмеченных точках.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Подсказка

а) Начните с небольших n = 1, 2, 3, … Постарайтесь заметить закономерность в последовательности чисел, равных количеству шестиугольников в каждом случае.
б) Рассмотрите частный случай: выясните, сколько шестиугольников определяют точки, расположенные на периметре правильного шестиугольника со стороной m, и, учитывая результат пункта а), найдите общее число всех шестиугольников.

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Решение

а) Итак, рассмотрим правильный шестиугольник H со стороной n, нарисованный на треугольной сетке. Посчитаем, сколько в нем содержится правильных шестиугольников со сторонами, параллельными сторонам H.

Ясно, что шестиугольник со стороной n всего один — он совпадает с H. Шестиугольников со стороной (n-1) уже 7 штук: у одного центр совпадает с центром H, а остальные получаются из него сдвигами к каждой из вершин H. Если продолжить уменьшать размер шестиугольника, то после аккуратного разбора случаев можно получить, что со стороной (n-2) будет 19 шестиугольников, а со стороной (n-3) — уже 37. Как возникают эти числа и что их объединяет?

Зафиксируем натуральное (k

Поскольку у каждого шестиугольника ровно одна левая нижняя вершина, то получается, что всего таких шестиугольников будет столько же, сколько узлов сетки попадает внутрь и на стороны шестиугольника со стороной (n-k).

Считать число точек внутри шестиугольника с данной стороной m можно разными способами. Мы последуем простому и изящному рассуждению, приведенному Мартином Гарднером в книге «Путешествие во времени». На рис. 3 все точки разбиты на четыре группы: те, что находятся в трех параллелограммах, плюс одна центральная точка. В одном параллелограмме (m(m-1)) точек, поэтому всего в шестиугольнике со стороной m будет (p_m=3m(m-1)+1=3m^2-3m+1) точек.

Нам, чтобы теперь решить задачу, нужно просуммировать эти выражения по всем m от 1 до n, то есть найти сумму (P=sumlimits_^n p_m). Удобнее всего это сделать, перегруппировав слагаемые так, чтобы отдельно сложить квадраты, отдельно — первые степени и отдельно — единицы:

Теперь осталось воспользоваться известными формулами для суммы чисел от 1 до n и для суммы их квадратов (см. задачу Суммы квадратов, суммы кубов. ):

После упрощения получится, что это выражение равно (n^3).

б) Надо заметить, что все точки, расположенные на периметре правильного шестиугольника со стороной m (где (minmathbb), (mle n)) определяют ровно m правильных шестиугольников (рис. 4). Верно и обратное: если на нашей сетке построен правильный шестиугольник, то его вершины обязательно будут лежать на сторонах другого шестиугольника, которые при этом параллельны сторонам H.

С учетом результатов пункта а) это означает, что надо найти сумму (N=sumlimits_^(p_cdot m)). Или, в полном виде:

Упрощать это выражение можно по-разному. Вот один из путей. Сначала выделим в отдельное слагаемое сумму, которую мы уже нашли в пункте а):

Сумма в первых скобках равна, как мы знаем, (n^3), и с учетом множителя n получится (n^4).

Разберемся со второй суммой. Компактно она записывается в виде (sumlimits_^ p_mcdot (m-1)). Но каждое слагаемое ( p_mcdot (m-1)=(3m^2-3m+1)(m-1)=3m^3-6m^2+4m-1) — это многочлен, а значит с этой суммой можно поступить так же, как мы делали в пункте а) — перегруппировать ее так, чтобы каждая степень складывалась отдельно:

Опять воспользуемся известными формулами для этих сумм и получим:

После упрощения останется следующее: (frac34n^4-frac12n^3-frac14n^2).

Поэтому искомое число всех правильных шестиугольников равно:

Видео:Все о правильном шестиугольнике за 1 минуту! #егэ2023 #математикапрофиль2023 #школаСкачать

Послесловие

Ненадолго отвлечемся от треугольных решеток и рассмотрим довольно естественно возникающий в контексте этой задачи вопрос: можно ли на обычной квадратной сетке (на построить правильный шестиугольник или треугольник так, чтобы все его вершины находились в узлах?

Оказывается, что нет. Краткое доказательство приводится ниже в скрытом виде, так что у вас остается возможность подумать самостоятельно над тем, почему это так.

Доказательство

Поскольку взятые через одну вершины правильного шестиугольника образуют правильный треугольник, то достаточно доказать, что не существует правильного треугольника с вершинами в узлах обычной квадратной решетки.

Допустим, что такой треугольник ABC все-таки существует. Тогда его площадь обязательно выражается рациональным числом. Это сразу следует из формулы Пика (см. статью Г. Мерзона Площади многоугольников и тающий лёд), но есть и простое наглядное рассуждение, не привлекающее такую «тяжелую артиллерию». Дело в том, что треугольник ABC достраивается до прямоугольника AMNK (достаточно провести через его вершины вертикальные и горизонтальные линии сетки, см. рис), площадь которого, очевидно, целая. При этом добавляются три прямоугольных треугольника (или два, если одна из сторон треугольника ABC идет по линии сетки), площади S₁, S₂ и S₃ которых либо целые, либо полуцелые. Значит, и площадь треугольника ABC сама тоже либо целая, либо полуцелая — и в любом случае рациональная.

С другой стороны, площадь правильного треугольника выражается через его сторону AB по формуле (AB^2sqrt3/4). Но по теореме Пифагора (AB^2=AM^2+MB^2) — целое число. Поскольку (sqrt3) — число иррациональное, то и площадь получается иррациональной. Получаем противоречие: одно и то же число (площадь ABC) не может быть одновременно рациональным и иррациональным.

Можно рассуждать и несколько по-другому. А именно, следить можно не за площадями, а за углами треугольника. Точнее, за их тангенсами. С одной стороны, как хорошо известно, угол равностороннего треугольника равен 60°, а его тангенс — (sqrt3). С другой стороны, аналогичным достроением до прямоугольника получим, что этот угол представляется как сумма (или разность — в зависимости от расположения треугольника ABC относительно линий сетки) двух углов, тангенсы которых рациональны. Из этого следует, что и этот угол должен быть рациональным (см. формулу тангенса суммы). Опять получается противоречие.

Вернемся к треугольной решетке. При внимательном ее рассмотрении обнаруживаются интересные свойства. Например, в каждом правильном шестиугольнике с вершинами в узлах решетки центр тоже является узлом. Кажется, что это очень простое наблюдение, но оно позволяет заметить большее. Оказывается, что число шестиугольников, имеющих центром некоторый узел, в точности равно значению выражения (h(h+1)/2), где h — расстояние от этого узла до ближайшей стороны исходного шестиугольника, а в качестве единицы измерения взята высота единичного треугольника сетки (рис. 5).

Это легко можно доказать, опираясь на факт, которым мы пользовались при решении пункта б): с центром в данном узле существует ровно h шестиугольников размера от 1 до h, стороны которых параллельны сторонам исходного шестиугольника H, а каждый из них «порождает», в соответствии с упомянутым фактом, число шестиугольников, равное его размеру. Значит, надо сложить числа от 1 до h, а это и даст выражение (h(h+1)/2). Числа такого вида называют треугольными.

Опираясь на эту находку, сделанную Сергеем Царановым, можно решить пункт б) еще одним способом. Для этого в каждом внутреннем узле решетки запишем число, равное количеству шестиугольников, имеющих центром данный узел (рис. 6, слева) — то есть соответствующее треугольное число T_k. Сумма всех записанных чисел будет равна числу всех правильных шестиугольников (будут посчитаны и те шестиугольники, стороны которых не лежат на линиях разбиения).

Но как сосчитать такую сумму? Можно так: все слагаемые разобьем на 6 одинаковых групп, заключенные в треугольные области, тогда искомая сумма равна увеличенной в 6 раз сумме всех чисел одной группы и плюс центральное число, не вошедшее ни в одну из групп (рис. 6, справа), которое равно T_n. Учитывая, что в группе по рядам записаны треугольные числа, получаем, что нужно посчитать сумму (sumlimits_^(T_icdot (n-i))). Это делается аналогично тому, как подсчитывались суммы в решении — получится (frac(n-1)n(n+1)(n+2)).

Значит, всего шестиугольников

Упрощая это выражение получим все тот же результат — (left(fracright)^2). Это, кстати, квадрат центрального треугольного числа.

Другой подход есть и к пункту а), причем он почти не требует вычислений. По аналогии с рис. 2 будем отмечать положения, которые может занимать центр шестиугольника (со сторонами, параллельными сторонам исходного шестиугольника), последовательно уменьшая его размер от n до 1 (рис. 7).

То есть для каждого размера мы имеем свое множество центров. Каждое из этих множеств можно представить себе по-другому: в виде трехгранного уголка, сложенного из единичных кубиков (рис. 8). Из таких уголков складывается кубик со стороной n. Это и дает ответ: n 3 шестиугольников.

С обсуждаемой задачей связана и придуманная автором головоломка «Разрушенные шестиугольники»: из спичек сложен правильный шестиугольник, разбитый на треугольные ячейки (рис. 9); какое наименьшее количество спичек надо убрать из этой конструкции, чтобы в ней не осталось ни одного контура правильного шестиугольника?

Попробуйте решить ее самостоятельно, опираясь на уже известные сведения о числе шестиугольников.

Решение головоломки

Как мы уже знаем, в шестиугольнике со стороной 3 есть 27 правильных шестиугольников: 19 со стороной 1 спичка, 7 со стороной 2 спички и 1 со стороной 3 спички. Заметим, что шесть спичек — по одной при каждой вершине исходного шестиугольника — не входят ни в один из этих 27 шестиугольников, поэтому ни одну из этих спичек нет смысла убирать.

Остальные спички можно представить в объединения трех неперекрывающихся групп спичек. В первой группе 6 шестиугольников со стороной 1 спичка, во второй группе 7 таких шестиугольников, в третьей группе — еще 6 (см. рис.).

Чтобы разрушить эти 19 шестиугольников, надо разбить их на смежные пары и в каждой паре убрать общую спичку, то есть надо убрать 3 + 4 + 3 = 10 спичек. После чего останется только один центральный шестиугольник со стороной 2, для разрушения которого надо убрать еще одну спичку. Значит, всего требуется убрать 11 спичек — например так, как показано на следующем рисунке.

Эта головоломка основана на исходной задаче при n = 3. При n = 1 и n = 2 она решается совсем просто, а вот уже при n = 4 возникают сложности и без компьютерного перебора справиться не получается. Возможно, у кого-то из читателей получится это сделать.