Радиус вектор центра тяжести (7 видео) | Курс школьной геометрии

Определение центра масс

При исследовании поведения систем частиц, часто удобно использовать для описания движения такую точку, которая характеризует положение и движение рассматриваемой системы как единого целого. Такой точкой служит центр масс.

Для однородных тел обладающих симметрией центр масс часто совпадает с геометрическим центром тела. В однородном изотропном теле одной выделенной точке найдется симметричная ей точка.

Содержание

Радиус-вектор и координаты центра масс
Скорость центра масс
Примеры задач на определение центра масс
Определения и формулы для вычисления центров тяжести
Определения и формулы для вычисления центров тяжести
Центр масс. Определение. Формула. Центр тяжести.
🌟 Видео

Видео:Радиус векторСкачать

Радиус-вектор и координаты центра масс

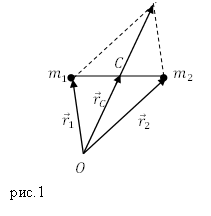
Предположим, что у нас имеются две частицы с равными массами, им соответствуют радиус-векторы: $<overline>_1 и <overline>_2$ . В этом случае центр масс расположен посередине между частицами. Центр масс (точка C) определён радиус-вектором $<overline>_C$ (рис.1).

Из рис.1 видно, что:

Можно ожидать, что вместе с геометрическим центром системы радиус-вектор, которого равен $<overline>_C,$ играет роль точка, положение которой определяет распределение массы. Ее определяют так, чтобы вклад каждой частицы был пропорционален ее массе:

Радиус -вектор $<overline>_C$, определенный выражением (2) — средне взвешенная величина радиус-векторов частиц $<overline>_1$ и $<overline>_2$. Это становится очевидным, если формулу (2) представить в виде:

Выражение (3) показывает, что радиус-вектор каждой частицы входит в $<overline>_C$ с весом, который пропорционален его массе.

Выражение (3) легко обобщается для множества материальных точек, которые расположены произвольным образом.

Если положения N материальных точек системы задано при помощи их радиус-векторов, то радиус — вектор, определяющий положение центра масс находим как:

Выражение (4) считают определением центра масс системы.

При этом абсцисса центра масс равна:

Ордината ($y_c$) центра масс и его аппликата ($z_c$):

Формулы (4-7) совпадают с формулами, которые используют для определения тяжести тела. В том случае, если размеры тела малы в сравнении с расстоянием до центра Земли, центр тяжести считают совпадающим с центром масс тела. В большинстве задач центр тяжести совпадает с центром масс тела.

Видео:Центр тяжести фигуры. Способ 1Скачать

Скорость центра масс

Выражение для скорости центра масс ($<overline>_c=frac<d<overline>_c>

$) запишем как:

где $overline

$ — суммарный импульс системы частиц; $M$ масса системы. Выражение (8) справедливо при движениях со скоростями которые существенно меньше скорости света.

Если система частиц является замкнутой, то сумма импульсов ее частей не изменяется. Следовательно, скорость центра масс при этом величина постоянная. Говорят, что центр масс замкнутой системы перемещается по инерции, то есть прямолинейно и равномерно, и это движение не зависимо от движения составных частей системы. В замкнутой системе могут действовать внутренние силы, в результате их действия части системы могут иметь ускорения. Но это не оказывает влияния на движение центра масс. Под действием внутренних сил скорость центра масс не изменяется.

Видео:Урок 79. Центр масс тела и методы определения его положенияСкачать

Примеры задач на определение центра масс

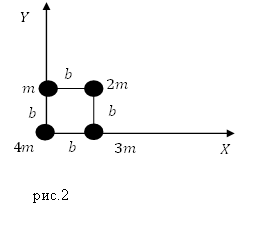
Задание. Система составлена из материальных точек (рис.2), запишите координаты ее центра масс?

Решение. Рассмотрим рис.2. Центр масс системы лежит на плоскости, значит, у него две координаты ($x_c,y_c$). Найдем их используя формулы:

Вычислим массу рассматриваемой системы точек:

Тогда абсцисса центра масс $x_ $равна:

Ответ. $x_c=0,5 b$; $y_с=0,3 b$

Задание. Космонавт, имеющий массу $m$, неподвижен относительно корабля массы $M$. Двигатель космического аппарата выключен. Человек начинает подтягиваться к кораблю при помощи легкого троса. Какое расстояние пройдет космонавт ($s_1$), какое корабль ($s_2$) до точки встречи? В начальный момент расстояние между ними равно $s$.

Решение. Центр масс корабля и космонавта лежит на прямой, соединяющей эти объекты.

В космосе, где внешние силы отсутствуют, центр масс замкнутой системы (корабль-космонавт) либо покоится, либо движется с постоянной скоростью. В избранной нами (инерциальной) системе отсчета он покоится. При этом:

Видео:2.4. Радиус-вектор и вектор перемещенияСкачать

Определения и формулы для вычисления центров тяжести

Видео:10 Класс - Физика - Перемещение. Радиус-вектор.Скачать

Определения и формулы для вычисления центров тяжести

Чтобы ввести понятие центроида, разделите рассматриваемый объект на достаточно большое количество мелких объектов по сравнению с объектом или базовой частью любой формы. Гравитация элементарных частиц с индексом I, обусловленная действием Земли, обозначается DR, -, а гравитация всего объекта — R. Гравитация элементарных частиц объекта практически направлена к центру Земли. Другими словами, это формирует систему конвергенции.

Давайте выясним, какие кривые C соединяют эти две точки, чтобы тяжелая материальная точка начиналась из точки A без начальной скорости. Людмила Фирмаль

Если размеры рассматриваемого объекта малы по сравнению с размером земного шара, гравитация элементарных частиц объекта может рассматриваться как система параллельных сил, направленных в одном направлении. Центр тяжести объекта является центром параллельной системы сил, образованной почти под действием силы тяжести его элементарных частиц. Радиус-вектор gf центра тяжести тела рассчитывается как радиус-вектор (рис. 88) центра параллельной силы по следующей формуле. £ г (DR, P Z Рисование Где r (радиус-вектор гравитационной точки действия базовой части тела, взятый за точку; DR — сила тяжести элементарных частиц; P = £ DR — сила тяжести всего тела.

Центр тяжести является точкой действия результирующей силы тяжести в случае силы тяжести.

r’ zc’r ’ Где xc, усы и zc — координаты центра тяжести. x ^ yh z — координаты точки приложения силы тяжести для DR (. Используйте концепцию центроида тела, чтобы представить концепцию центроида.

Основная часть тела и гравитация всего тела могут быть выражены через массу At, M и ускорение свободного падения g, используя следующие уравнения: DR, = Am, г, P = Mg. Подставляя эти значения силы тяжести в (1) и (G) после уменьшения на g, которое предполагается одинаковым во всех частях тела, (2) В соответствии с этим (2 ‘) Уравнения (2) и (2 ‘) определяют радиус-вектор центра тяжести объекта. Центроид обычно определяется как радиус-вектор, который является геометрической точкой, независимой от центроида. Это рассчитывается по уравнению (2) или (2 ‘). В проекции на оси координат из (2) и (2 ‘) вы получите: £ X / дм, XY ^ m1 £ 2 , Где v — объем тела Присвойте эти значения (2) и (2 ‘). После уменьшения y „и p„, получите формулу соответственно.

После того как Ньютон сформулировал основные законы классической механики, их применение к несвободным твердым и механическим системам стало затруднительным до тех пор, пока не были сформулированы аксиомы связи. Людмила Фирмаль

Определить центр тяжести тела. Если тело имеет форму поверхности, то есть, если один из размеров меньше двух других, например тонкий лист железа, ДР,. = У5Д5 „P = ysS, где ys — удельный вес. D5; — площадь элементарных частиц на поверхности S — общая площадь поверхности. Получите следующее выражение: Для однородного тела, такого как провод, размер которого на два меньше по сравнению с третьим, можно определить радиус-вектор для центроида длины линии, используя следующую формулу: £ W fc = -! -. Где D / (длина элемента строки. Серьезность определяется. I — Общая длина линии, центр.

Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:Радиус-векторыСкачать

Центр масс. Определение. Формула. Центр тяжести.

Центр масс это геометрическая точка находящаяся внутри тела, которая определяет распределение массы этого тела. Любое тело можно представить в виде суммы некоторого количества материальных точек. В этом случае положение центра масс определяет радиус вектор.

mi — масса итой точки.

ri — радиус вектор итой точки.

Если просуммировать массы всех материальных точек, то получится масса всего тела. На положение центра масс влияет однородность распределения массы по объему тела. Центр масс может находиться как внутри тела, так и за его приделами. Скажем у кольца, центр масс находится в центре окружности. Там где нет вещества. В общем, для симметричных тел обладающих однородным распределением массы центр масс всегда находится в центре симметрии или на ее оси.

Если к телу прикладывать некоторую силу, то оно начнет двигаться. Представьте себе кольцо, лежащее на поверхности стола. Если к нему приложить силу, а попросту начать толкать, то оно будет скользить по поверхности стола. А вот направление движения будет завесить от места приложения силы.

Если силу направить от внешнего края к центру, по перпендикуляру к внешней поверхности, то кольцо начнет прямолинейно двигаться по поверхности стола в направлении приложения силы. Если же силу приложить по касательной к внешнему радиусу кольца, то оно начнет поворачиваться относительно своего центра масс. Таким образом, можно заключить, что движение тела состоит из суммы поступательного движения и вращательного относительно центра масс. То есть движение любого тела можно описать движением материальной точки находящейся в центре масс и имеющей массу всего тела.

Существует также понятие центр тяжести. В общем, это не одно и то же что и центр масс. Центр тяжести это точка относительно, которой общий момент силы тяжести равен нулю. Если представить себе стержень длинной скажем 1 метр, диаметром 1см, и однородный по своему сечению. На концах стержня закреплены металлические шары одинаковой массы. То центр масс этого стержня будет находиться посередине. Если этот стержень поместить в неоднородное гравитационное поле, то центр тяжести будет смещён в сторону большей напряжённости поля.

На поверхности земли, где сила тяжести однородна, центр масс практически совпадает с центром тяжести. Для любого постоянного однородного гравитационного поля центр тяжести всегда будет совпадать с центром масс.