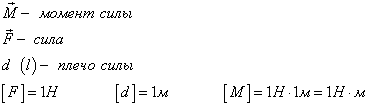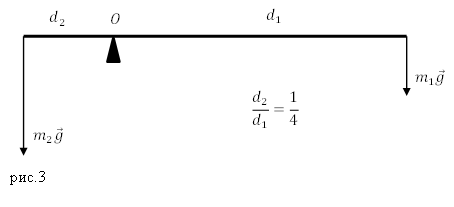Радиус вектор действия силы плечо силы

Видео:Статика. Что такое плечо силы?Скачать

I. Механика

Видео:Момент силыСкачать

Тестирование онлайн

Видео:Момент силы. Определение, размерность и знаки. Плечо силыСкачать

Плечо силы

Плечо силы — это длина перпендикуляра из некоторой вымышленной точки О к силе. Вымышленный центр, точку О, будем выбирать произвольно, моменты каждой силы определяем относительно этой точки. Нельзя для определения моментов одних сил выбрать одну точку О, а для нахождения моментов других сил выбрать ее в другом месте!

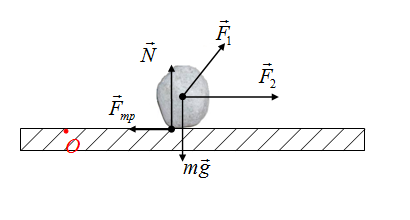
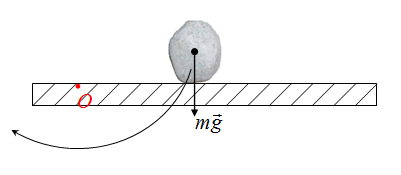
На камень действуют сила тяжести, сила трения, сила реакции опоры, две дополнительные внешние силы F₁ и F₂

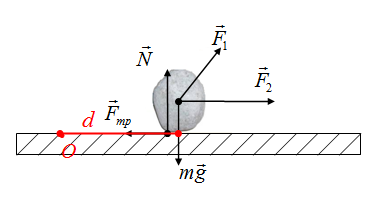
Выбираем точку О в произвольном месте, больше ее местоположение не изменяем. Тогда плечо силы тяжести — это длина перпендикуляра (отрезок d) на рисунке

Плечо силы реакции опоры определяется аналогично

Если перпендикуляр нет возможности построить, то вектор силы продлевается в необходимом направлении, после чего строим перпендикуляр к этой линии. Плечо силы F₂

Осталась сила трения! Если точка О и сила лежат на одной линии, то плечо этой силы равно нулю. Плечо силы трения равно нулю.

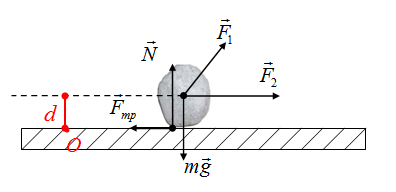
При решении задач выгодно точку О выбирать в точке пересечения нескольких сил. Тогда плечи всех этих сил будут нулевыми. Например, если точку О в предыдущем примере выбрать иначе, то плечи сил будут иными.

Плечи сил F₁, F₂ и силы тяжести равны нулю, так как точка О лежит с ними на одной прямой (или на самой силе). Плечо силы реакции опоры — это длина d₁. Плечо силы трения — это длина d₂.

Видео:10 Класс - Физика - Перемещение. Радиус-вектор.Скачать

Момент силы

Это векторная величина, определяется по формуле

Направление вектора момента силы определяется следующим образом. Представляем в какую сторону сила пытается повернуть (тащить) тело относительно точки О, если тело с точкой О закреплены осью. Если по часовой стрелки, то вектор имеет знак «+», если против часовой, тогда знак «-«.

Момент силы реакции опоры отрицательный, так как сила реакции опоры «поворачивает» тело против часовой стрелки

Момент силы тяжести положительный, так как сила тяжести «поворачивает» тело по часовой стрелки

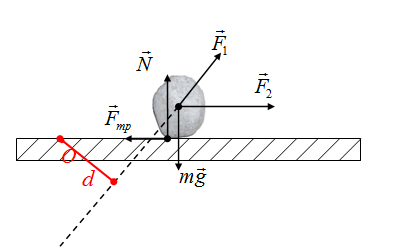
Если точка О выбрана на теле

Момент силы реакции опоры и силы трения положительные, так как силы «поворачивают» тело по часовой стрелки

Видео:Момент силы относительно точкиСкачать

Основные понятия и опреде­ления статики.

Видео:Момент силы относительно точки и осиСкачать

1. Основные понятия и определения статики.

Материальные объекты в статике:

система материальных точек,

абсолютно твердое тело.

Системой материальных точек, или механической системой, называется такая совокупность материальных точек, в которой положение и движение каждой точки зависит от положения и движения других точек этой системы.

Абсолютно твердое тело – это тело, расстояние между двумя точками которого не изменяется.

Твердое тело может находиться в состоянии покоя или движения определенного характера. Каждое их этих состояний будем называть кинематическим состоянием тела .

Сила — мера механического взаимодействия тел, определяющая интенсивность и направление этого взаимодействия.

Сила может быть приложена в точке, тогда эта сила – сосредоточенная.

Сила может действовать на все точки данного объема или поверхности тела, тогда эта сила – распределенная.

Система сил — совокупность сил, действующих на данное тело.

Равнодействующей называется сила, эквивалентная некоторой системе сил.

Уравновешивающей силой называется сила, равная по модулю равнодействующей и направленная по линии ее действия в противоположную сторону.

Системой взаимно уравновешивающихся сил называется система сил, которая будучи приложенной к твердому телу, находящемуся в покое, не выводит его из этого состояния.

Внутренние силы – это силы, которые действуют между точками или телами данной системы.

Внешние силы – это силы, которые действуют со стороны точек или тел, не входящих в данную систему.

Видео:2.4. Радиус-вектор и вектор перемещенияСкачать

Задачи статики:

— преобразование систем сил, действующих на твердое тело в эквивалентные им системы;

— исследование условий равновесия тел под действием приложенных к ним сил.

Видео:Урок 80 (осн). Момент силы. Правило моментовСкачать

1. Аксиомы статики.

1. Аксиома инерции . Под действием взамно-уравновешивающихся сил материальная точка (тело) находится в состоянии покоя или движется прямолинейно и равномерно.

2. Аксиома равновесия двух сил . Две силы, приложенные к твердому телу взаимно уравновешиваются только в том случае, если их модули равны и они направлены по одной прямой в противоположные стороны.

3. Аксиома присоединения и исключения уравновешивающихся сил . Действие системы сил на твердое тело не изменится, если к ней присоединить или из нее исключить систему взаимно-уравновешивающихся сил.

Следствие . Не изменяя кинематического состояния абсолютно твердого тела, силу можно переносить вдоль линии ее действия, сохраняя неизменным ее модуль и направление.

Сила — скользящий вектор.

4. Аксиома параллелограмма сил . Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах.

5. Аксиома равенства действия и противодействия . Всякому действию соответствует равное и противоположно направленное противодействие.

Видео:Момент силыСкачать

2. Связи и их реакции

Твердое тело называется свободным , если оно может перемещаться в пространстве в любом направлении.

Тело, ограничивающее свободу движения данного твердого тела, является по отношению к нему связью .

Твердое тело, свобода движения которого ограничено связями, называется несвободным .

Все силы, действующие на несвободное твердое тело, можно разделить на:

• задаваемые (активные)
• реакции связей

Задаваемая сила выражает действие на данное тело других тел, способных вызвать изменение его кинематического состояния.

Реакция связи – это сила, с которой данная связь действует на тело, препятствуя тем или иным его перемещениям.

Принцип освобождаемости твердых тел от связей — несвободное твердое тело можно рассматривать как свободное, на которое кроме задаваемых сил, действуют реакции связей.

Как определить направление реакции?

Если существует два взаимно перпендикулярных направления на плоскости, в одном из которых связь препятствует перемещению тела, а в другом нет, то направление ее реакции противоположно первому направлению.

В общем случае направлена реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу.

Видео:Эффект Джанибекова [Veritasium]Скачать

Формула плеча силы

Видео:Лекция 4.1 | Радиус-вектор, скорость и ускорение | Александр Чирцов | ЛекториумСкачать

Определение и формула плеча силы

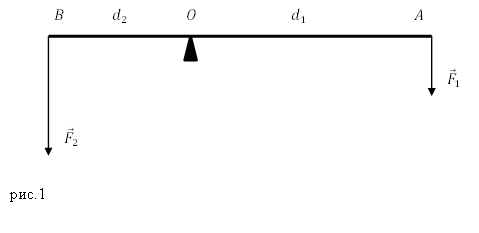
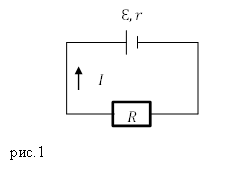
Рассмотрим рычаг с осью вращения находящийся в точке О. (рис.1). Силы $<overline>_1$ и $<overline>_2$, действующие на рычаг направлены в одну сторону.

Минимальное расстояние между точкой опоры (точка О) и прямой, вдоль которой действует на рычаг сила, называют плечом силы.

Для нахождения плеча силы следует из точки опоры опустить перпендикуляр к линии действия силы. Длинна данного перпендикуляра и станет плечом рассматриваемой силы. Так, на рис.1 расстояние $left|OAright|=d_1$- плечо силы $F_1$; $left|OAright|=d_2$- плечо силы $F_2$.

Рычаг находится в состоянии равновесия, если выполняется равенство:

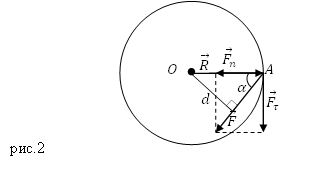
Предположим, что материальная точка движется по окружности (рис.2) под действием силы $overline$ (сила действует в плоскости движения точки). В таком случае угловое ускорение ($varepsilon $) точки определяется тангенциальной составляющей ($F_$) силы $overline$:

где $m$ — масса материальной точки; $R$ — радиус траектории движения точки; $F_$ — проекция силы на направление скорости движения точки.

Если угол $alpha $ — это угол между вектором силы $overline$ и радиус — вектором $overline$, определяющим положение рассматриваемой материальной точки (Этот радиус- вектор проведен из точки О в точку А на рис.2), тогда:

Расстояние $d$ между центром O и линией действия силы $overline$ называют плечом силы. Из рис.2 следует, что:

Если на точку будет действовать сила ($overline$), направленная по касательной к траектории ее движения, то плечо силы будет равно $d=R$, так как угол $alpha $ станет равен $frac$.

Видео:Момент импульса и момент силы относительно точки и оси | Студенты, абитуриенты МФТИ | Вуз. физика #1Скачать

Момент силы и плечо

Понятие плечо силы иногда используют, для записи величины момента силы ($overline$), который равен:

где $overline$ — радиус — вектор проведенный к точке продолжения силы$ overline$. Модуль вектора момента силы равен:

Видео:Центр тяжести тела. Условия равновесия тел | Физика 7 класс #46 | ИнфоурокСкачать

Построение плеча силы

И так, плечом силы называют длину перпендикуляра, который проводят из некоторой выбранной точки, иногда ее называют полюсом (выбираемой произвольно, но при рассмотрении одной задачи один раз). При рассмотрении задач точку О выбирают обычно на пересечении нескольких сил) к силе (рис.3 (а)). Если точка О будет лежать на одной прямой с силами или на самой силе, то плечи сил будут равны нулю.

Если перпендикуляр не получается построить, то вектор силы продлевают в нужном направлении, после этого строят перпендикуляр (рис.3 (б)).

Видео:§4.3. Главный вектор и главный момент сил инерцииСкачать

Примеры задач с решением

Задание. Какова масса меньшего тела ($m_1$), если его уравновешивает тело массой $m_2=$кг? Тела находятся на невесомом рычаге (рис.3) отношение плеч рычага 1:4?

Решение. Основой решения задачи является правило равновесия рычага:

где силы, действующие на концы рычага равны по модулю силам тяжести, которые действуют на тела, следовательно, формулу (1.1) перепишем в виде:

Из выражения (1.2) получим искомую массу $m_1$:

Вычислим искомую массу:

Ответ. $m_1=0,5 кг$

Задание. Однородный стержень длинной $l $и массой $M$ расположен горизонтально. Один конец стержня в точке А закреплён так, что может вращаться вокруг этой точки, другой конец опирается на наклонную плоскость, угол наклона которой к горизонту равен $alpha $. На стержне на расстоянии $b $от точки А лежит небольшой груз. Каковы плечи сил, действующих на стержень?

Решение. Изобразим на рис.4 силы, действующие на стержень. Это: сила тяжести: $Moverline$, вес груза, расположенного на нем $overline

=m_1overline$, сила реакции наклонной плоскости: $overline$; сила реакции опоры в точке A: $overline’$.

Плечи сил будем искать относительно точки A. Плечо силы $overline$ будет равно нулю, так как сила приложена к стержню в точке А:

Плечо другой силы реакции опоры ($overline$) равно длине перпендикуляра AC:

Плечо силы $Moverline$ из рис.4 , так как сила тяжести приложена к центру масс стержня, который для однородного стержня находится на его середине:

Плечо силы $m_1overline,$ учитывая, что груз маленький и принимая его за материальную точку, равно:

🎬 Видео

Вращательное движение. 10 класс.Скачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Котика ударило током, 10 т. ВольтСкачать

Момент силы: почему его так назвали ?Скачать

Момент инерцииСкачать

ЕГЭ по Физике 2022. Кинематика. Радиус-векторСкачать