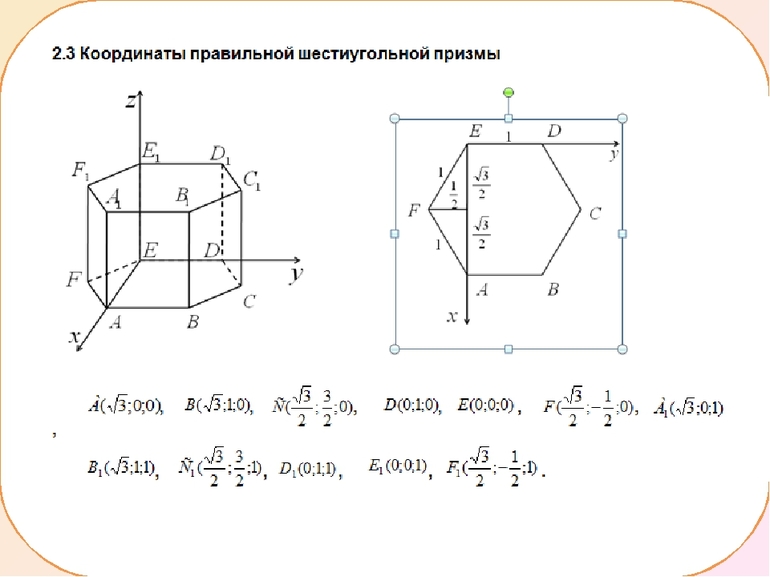
Одним из фундаментальных объектов в геометрии является многоугольник. Если рассматривать фигуру в трёхмерном пространстве, то с помощью двух таких геометрических тел с шестью углами можно построит правильную шестиугольную призму. При этом боковые грани обязательно будут прямоугольниками. По своему виду такая фигура напоминает пчелиные соты, поэтому она и интересна для изучения архитекторам и математикам.
- Общие сведения
- Свойства шестигранника
- Решение простого примера
- Задача высокого уровня
- Правильная шестиугольная призма — свойства, признаки и формулы
- Общие сведения
- Свойства шестигранника
- Решение простого примера
- Задача высокого уровня
- Радиус окружности, описанной около основания правильной шестиугольной призмы, равен 3см?
- Цилиндр вписан в правильную четырехугольную призму?
- Шестиугольная и треугольная правильные призмы имеют равные высоты и равные площади боковых поверхностей?
- Найдите площадь боковой и полной поверхности правильной треугольной призмы с высотой h = 10, если радиус окружности, вписанной в основание, равен r = 9 см?
- Сторона основания правильной шестиугольной призмы равна a, боковое ребро равно b?
- Основанием прямой треугольной призмы служит прямоугольный треугольник с гипотенузой 17 см и катетом 8 см?
- Основанием прямой треугольной призмы служит прямоугольный треугольник с гипотенузой 17 см и катетом 8 см?
- В правильной треугольной призме сторона основания равна 5 см , а высота призмы равна 12 см ?
- В правильной треугольной призме сторона основания равна 9 ДМ, а высота 11 ДМ?
- Вычислить площади боковой и полной поверхности правильной 4 — х угольной призмы имеющей высоту, равную 25 см, радиус описанной около основания окружности 8 см?
- Около шара радиусом 4 см описана правильна треугольная призма ?
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Общие сведения
Призма представляет собой многогранную объёмную фигуру. Две стороны её всегда конгруэнтные (равные) и расположены относительно друг друга в параллельных плоскостях. Остальные же грани являются параллелограммами и формируют общие боковые основания с параллельными поверхностями. Четырёхугольники состоят из попарно равноудалённых прямых. Называют их боковыми гранями призмы. Оставшиеся же 2 многоугольника — основанием. По сути, фигура — это частный случай некругового цилиндра.
Кроме основания и граней, в состав стереофигуры входит:
- высота — прямая, перпендикулярная плоскостям, лежащим у основания многогранника;
- боковые рёбра — стороны, являющиеся общими для боковых граней;
- вершины — точки, принадлежащие сразу двум отрезкам и формирующим периметр геометрического тела;
- диагонали — отрезки, проходящие через 2 вершины, но при этом несвойственные одной грани;
- диагональные плоскости — пересекающие боковые рёбра и диагональ у основания.
Кроме этого, используются такие понятия, как диагональное и ортогональное сечение. Первое представляет собой параллелограмм, полученный при пересечении призмы и диагональной плоскости. Второе же — пересечение многогранника с плоскостью, перпендикулярной боковому ребру.
В зависимости от расположения стенок и вида основания, призмы разделяют на 3 типа. Прямой называют ту, где все грани — прямоугольники. Если у фигуры в основании находится правильный многоугольник, стереофигура считается правильной. Частным случаем её является полуправильная призма. В ней боковые грани образуют квадраты. Когда же у многогранника основания непараллельные, призму называют усечённой.
Полуправильный многогранник, имеющий 2 параллельных основания в виде правильных n-угольников, равных между собой, чьи грани представляют собой ломаную линию, называют антипризмой. В качестве примера такой фигуры можно привести октаэдр, икосаэдр и восьмиугольный октагон.
Видео:Радиус описанной окружностиСкачать

Свойства шестигранника
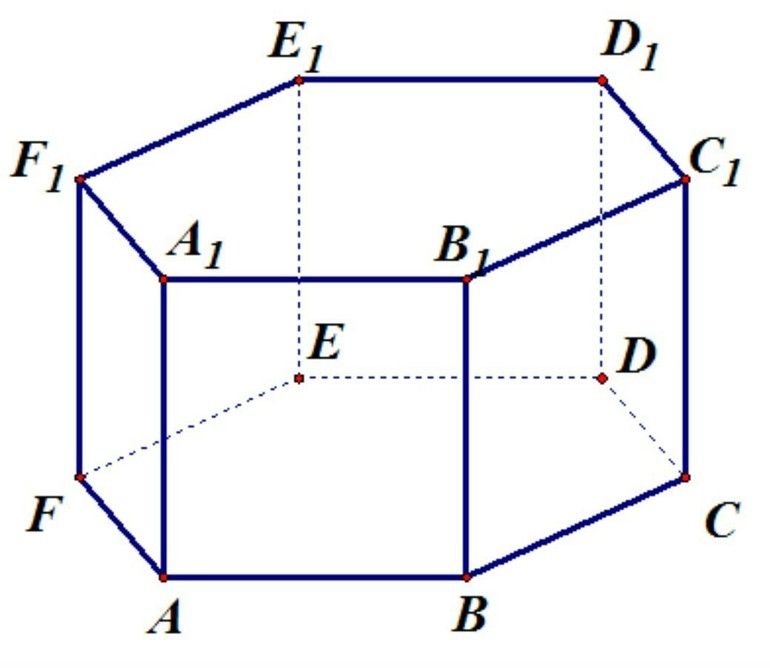
Правильную шестиугольную призму принято обозначать большими латинскими буквами: ABCDEFA1B1C1D1E1F1. Длину основания подписывают маленьким символом a, а длину боковой стороны h. К характеристикам фигуры относят площади основания, боковые грани, полную поверхность, объём многогранника. Всего у геометрического тела 8 граней, 18 рёбер и 12 вершин.
Для успешного вычисления различных параметров фигуры понадобится знать следующие формулы:
Если рассмотреть правильный шестиугольник, лежащий в основе призмы ABCDEF, и провести отрезки AB, CD, EF, у них будет общая точка пересечения. Для удобства обозначить её можно буквой O. Так как, в соответствии со свойствами, треугольники AOB, BOC, COD, DOE, EOF, FOA будут правильными, можно составить равенство: AO = OD = EO = OB = CO = OF = a .
Через точку М можно провести прямую AC и CF. Образованный ранее треугольник AEO будет равнобедренным. В нём отрезок AO равняется по величине OE. Значит, угол EOA будет развёрнутым и равняться 120 градусам. Используя свойства равнобедренного треугольника, можно записать: AE = a * √2 * (1 — cos EOA). То есть: AE = AC = √3 * a.
По аналогии можно найти и стороны: EA1, FB1, AC1, BD1, CE1, DF1. Так как AA1 = h, а из свойств правильной призмы следует, что угол EAA1 — прямой, длины сторон будут равны между собой, и их можно найти, используя формулу: √(AA1 2 + AE 2 )= √(h 2 + 3 * a) = 2 * a. Грань EB1 = FC1 = AD1 = BE1 = CF1 = DA1 = √(BB1 2 + BE 2 ) = √(h 2 + 4 *a) = √5 *a. Сторона FE1 = √(FE 2 + EE 2 ) = √(h 2 + a 2 ) = √2 *a.
Длины диагоналей призмы равняются сумме квадратов высоты и длины основания под корнем. Это легко доказать, если принять, что ЕЕ1 = h, а FE = a. Треугольник FEE1 прямоугольный, значит, FE = √(h 2 + a 2 ), что и следовало доказать.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Решение простого примера
Такого вида задачи обычно даются в учебниках по геометрии для выпускных классов средней школы. Решить их самостоятельно несложно, нужно только знать формулы и представлять, как выглядит та или иная фигура. При этом часто приходится использовать дополнительные построения. Вот один из таких типовых примеров.
Пусть имеется девятиугольная фигура, в которую вписана правильная шестиугольная призма со стандартным обозначением вершин. Сторона основания в ней составляет 4 см, а длина бокового ребра меньше её в 2 раза, то есть равняется 2. Необходимо вычислить расстояние от точки C1 до прямой, соединяющей вершины EF. По условию задачи в основании лежит геометрическое тело, у которого все стороны и углы равны, то есть фигура правильная.
Чтобы понять, что будет представлять искомая прямая, нужно изобразить призму на рисунке и на нём же начертить отрезок. Фактически это будет перпендикуляр, который и является вычисляемым расстоянием. Проекцией точки С1 будет вершина С. Из неё можно построить перпендикуляр, который ограничится точкой E. Таким образом, поставленная задача сводится к поиску длины отрезка C1E.
Найти длину прямой можно как гипотенузу прямоугольного треугольника С1СE. Треугольная фигура будет с прямым углом C. Из условия задачи отрезок С1С в два раза меньше ребра основания, а значит равен 2. Теперь осталось найти, чему равняется длина CE. Геометрическое тело CDE является равнобедренным. По условию CD = ED. Сумму углов шестиугольника можно найти по формуле е = 180 * (n — 2) = 180 * 4 = 720. Получается, что на каждый угол приходится по 120 градусов.
С вершины D можно опустить перпендикуляр DN на CE. Принимая во внимание свойства равнобедренного треугольника, высота DN будет медианной и биссектрисой. Следовательно, угол C равняется 30 градусов, так как CDH — прямоугольный.
Теперь можно найти СH. Сделать это возможно через косинус угла C: cos 30 = CH / CD. Отсюда: CH = 4 * p/2 = 2 √ 3. Так как CH = HE, сторона CE = 2 * 2 √3. К треугольнику CC1E можно применить теорему Пифагора: C1E 2 = C1C 2 + CE = 2 2 + (4 c3) 2 . C1E 2 = √ 52. Таким образом, искомый ответ можно записать так: C1E = 2√13.
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Задача высокого уровня
Решение примеров повышенного уровня сложности предполагает не только хорошее понимание изучаемого материала, но и знание предыдущих тем. Понадобится вспомнить формулы для нахождения площадей и объёмов плоских фигур и их свойства. Вот пример одной из таких задач.
Пусть имеется шестиугольная объёмная фигура, у которой баковая грань равняется 6, а площадь основания 12. Нужно найти объём геометрического тела с вершинами в точках A, B1, C1, D1, E1, F1.
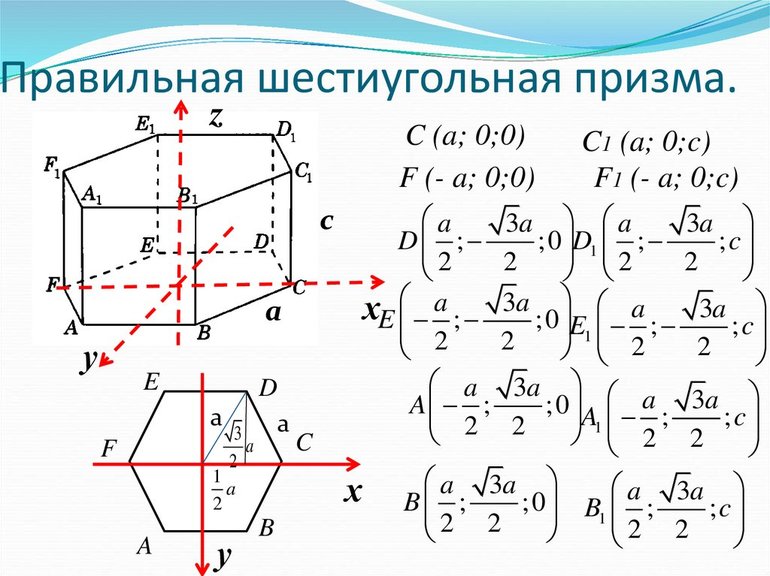
В таких задачах перед тем как непосредственно приступить к вычислениям, желательно использовать вспомогательный рисунок. На нём нужно изобразить фигуру в трёхмерной системе координат и подписать все её вершины.
Согласно условию, площадь основания Sabcde1f1 = 12, отрезок AA1 = 6. Так как фигура правильная, то все ребра у призмы буду равны. Чтобы найти, сколько будет составлять объём, понадобится обозначить многогранник. Для этого следует построить отрезки F1B, F1A, B1, E1A, D1A, C1A. Получившаяся фигура представляет собой пирамиду.
Формула для нахождения объёма пирамиды записывается так: V = h * S / 3. Её можно привести к виду: V = (AA1 * Sb1c1d1e1f1) / 3. Теперь нужно определить, чему же будет равняться площадь шестиугольника. Так как в основании призмы лежит правильная фигура с шестью углами, радиус описанной окружности будет совпадать с боковой стороной.
Таким образом, искомая площадь будет равняться шести поверхностям правильного треугольника. В свою очередь, его занимаемый размер можно определить как Sтр = (a * b) * sin / 2. Значит, площадь основания призмы равна: S = (6 * R * R * sin 60) / 2. Подставив заданное условием значение из формулы, можно выразить радиус: R 2 = (12 * 2) / 3 √ 3 = 8 /√3.
Площадь треугольника A1B1F1 находится как произведение сторон, умноженное на синус угла и разделённое на 2: S = (a * a * sin120) / 2 = a 2 * sin60 / 2 = (R 2 * √ 3/3) / 2. Подставив значение R, можно получить: S = (½) * (8 / √ 3) * (√3 / 2) = 2. Тогда площадь пятиугольника будет равняться разнице поверхностей шестиугольника и треугольника A1B1F1, то есть S = 12 — 2 = 10. Теперь можно будет подсчитать и объём пирамиды: Vab1c1d1e1f1 = (1 / 3) * 6 * 10 = 20. Задача решена.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Правильная шестиугольная призма — свойства, признаки и формулы
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Общие сведения
Призма представляет собой многогранную объёмную фигуру. Две стороны её всегда конгруэнтные (равные) и расположены относительно друг друга в параллельных плоскостях. Остальные же грани являются параллелограммами и формируют общие боковые основания с параллельными поверхностями. Четырёхугольники состоят из попарно равноудалённых прямых. Называют их боковыми гранями призмы. Оставшиеся же 2 многоугольника — основанием. По сути, фигура — это частный случай некругового цилиндра.
Кроме основания и граней, в состав стереофигуры входит:
- высота — прямая, перпендикулярная плоскостям, лежащим у основания многогранника;
- боковые рёбра — стороны, являющиеся общими для боковых граней;
- вершины — точки, принадлежащие сразу двум отрезкам и формирующим периметр геометрического тела;
- диагонали — отрезки, проходящие через 2 вершины, но при этом несвойственные одной грани;
- диагональные плоскости — пересекающие боковые рёбра и диагональ у основания.
Кроме этого, используются такие понятия, как диагональное и ортогональное сечение. Первое представляет собой параллелограмм, полученный при пересечении призмы и диагональной плоскости. Второе же — пересечение многогранника с плоскостью, перпендикулярной боковому ребру.
В зависимости от расположения стенок и вида основания, призмы разделяют на 3 типа. Прямой называют ту, где все грани — прямоугольники. Если у фигуры в основании находится правильный многоугольник, стереофигура считается правильной. Частным случаем её является полуправильная призма. В ней боковые грани образуют квадраты. Когда же у многогранника основания непараллельные, призму называют усечённой.
Полуправильный многогранник, имеющий 2 параллельных основания в виде правильных n-угольников, равных между собой, чьи грани представляют собой ломаную линию, называют антипризмой. В качестве примера такой фигуры можно привести октаэдр, икосаэдр и восьмиугольный октагон.
Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Свойства шестигранника
Правильную шестиугольную призму принято обозначать большими латинскими буквами: ABCDEFA1B1C1D1E1F1. Длину основания подписывают маленьким символом a, а длину боковой стороны h. К характеристикам фигуры относят площади основания, боковые грани, полную поверхность, объём многогранника. Всего у геометрического тела 8 граней, 18 рёбер и 12 вершин.
Для успешного вычисления различных параметров фигуры понадобится знать следующие формулы:
- Площадь основания. Так как в основе тела лежат правильные шестиугольники, то, используя их свойства, можно получить формулу: S = (3 * a 2 * √ 3) / 2, где: а — сторона многоугольника.
- Площадь полной поверхности. Определяется она из равенства: Sb = 6 * a * h + 2 * (3 * a 2 * √ 3) / 2. Из-за того, что площадь плоскости можно получить путём сложения сторон призмы и двух поверхностей её основания, а грань — прямоугольник (S прямоугольника = a * h), то указанная формула будет верной.
- Объём. Он равняется произведению площади основания на высоту. Роль последней может играть ребро любой стороны, например, BB1. Учитывая сказанное, формулу можно записать так: V = S * BB 1 = ((3 √ 3) / 2) * (a 2 * h).
Если рассмотреть правильный шестиугольник, лежащий в основе призмы ABCDEF, и провести отрезки AB, CD, EF, у них будет общая точка пересечения. Для удобства обозначить её можно буквой O. Так как, в соответствии со свойствами, треугольники AOB, BOC, COD, DOE, EOF, FOA будут правильными, можно составить равенство: AO = OD = EO = OB = CO = OF = a .
Через точку М можно провести прямую AC и CF. Образованный ранее треугольник AEO будет равнобедренным. В нём отрезок AO равняется по величине OE. Значит, угол EOA будет развёрнутым и равняться 120 градусам. Используя свойства равнобедренного треугольника, можно записать: AE = a * √2 * (1 — cos EOA). То есть: AE = AC = √3 * a.
По аналогии можно найти и стороны: EA1, FB1, AC1, BD1, CE1, DF1. Так как AA1 = h, а из свойств правильной призмы следует, что угол EAA1 — прямой, длины сторон будут равны между собой, и их можно найти, используя формулу: √(AA1 2 + AE 2 )= √(h 2 + 3 * a) = 2 * a. Грань EB1 = FC1 = AD1 = BE1 = CF1 = DA1 = √(BB1 2 + BE 2 ) = √(h 2 + 4 *a) = √5 *a. Сторона FE1 = √(FE 2 + EE 2 ) = √(h 2 + a 2 ) = √2 *a.
Длины диагоналей призмы равняются сумме квадратов высоты и длины основания под корнем. Это легко доказать, если принять, что ЕЕ1 = h, а FE = a. Треугольник FEE1 прямоугольный, значит, FE = √(h 2 + a 2 ), что и следовало доказать.
Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Решение простого примера
Такого вида задачи обычно даются в учебниках по геометрии для выпускных классов средней школы. Решить их самостоятельно несложно, нужно только знать формулы и представлять, как выглядит та или иная фигура. При этом часто приходится использовать дополнительные построения. Вот один из таких типовых примеров.
Пусть имеется девятиугольная фигура, в которую вписана правильная шестиугольная призма со стандартным обозначением вершин. Сторона основания в ней составляет 4 см, а длина бокового ребра меньше её в 2 раза, то есть равняется 2. Необходимо вычислить расстояние от точки C1 до прямой, соединяющей вершины EF. По условию задачи в основании лежит геометрическое тело, у которого все стороны и углы равны, то есть фигура правильная.
Чтобы понять, что будет представлять искомая прямая, нужно изобразить призму на рисунке и на нём же начертить отрезок. Фактически это будет перпендикуляр, который и является вычисляемым расстоянием. Проекцией точки С1 будет вершина С. Из неё можно построить перпендикуляр, который ограничится точкой E. Таким образом, поставленная задача сводится к поиску длины отрезка C1E.
Найти длину прямой можно как гипотенузу прямоугольного треугольника С1СE. Треугольная фигура будет с прямым углом C. Из условия задачи отрезок С1С в два раза меньше ребра основания, а значит равен 2. Теперь осталось найти, чему равняется длина CE. Геометрическое тело CDE является равнобедренным. По условию CD = ED. Сумму углов шестиугольника можно найти по формуле е = 180 * (n — 2) = 180 * 4 = 720. Получается, что на каждый угол приходится по 120 градусов.
С вершины D можно опустить перпендикуляр DN на CE. Принимая во внимание свойства равнобедренного треугольника, высота DN будет медианной и биссектрисой. Следовательно, угол C равняется 30 градусов, так как CDH — прямоугольный.
Теперь можно найти СH. Сделать это возможно через косинус угла C: cos 30 = CH / CD. Отсюда: CH = 4 * p/2 = 2 √ 3. Так как CH = HE, сторона CE = 2 * 2 √3. К треугольнику CC1E можно применить теорему Пифагора: C1E 2 = C1C 2 + CE = 2 2 + (4 c3) 2 . C1E 2 = √ 52. Таким образом, искомый ответ можно записать так: C1E = 2√13.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Задача высокого уровня
Решение примеров повышенного уровня сложности предполагает не только хорошее понимание изучаемого материала, но и знание предыдущих тем. Понадобится вспомнить формулы для нахождения площадей и объёмов плоских фигур и их свойства. Вот пример одной из таких задач.
Пусть имеется шестиугольная объёмная фигура, у которой баковая грань равняется 6, а площадь основания 12. Нужно найти объём геометрического тела с вершинами в точках A, B1, C1, D1, E1, F1.
В таких задачах перед тем как непосредственно приступить к вычислениям, желательно использовать вспомогательный рисунок. На нём нужно изобразить фигуру в трёхмерной системе координат и подписать все её вершины.
Согласно условию, площадь основания Sabcde1f1 = 12, отрезок AA1 = 6. Так как фигура правильная, то все ребра у призмы буду равны. Чтобы найти, сколько будет составлять объём, понадобится обозначить многогранник. Для этого следует построить отрезки F1B, F1A, B1, E1A, D1A, C1A. Получившаяся фигура представляет собой пирамиду.
Формула для нахождения объёма пирамиды записывается так: V = h * S / 3. Её можно привести к виду: V = (AA1 * Sb1c1d1e1f1) / 3. Теперь нужно определить, чему же будет равняться площадь шестиугольника. Так как в основании призмы лежит правильная фигура с шестью углами, радиус описанной окружности будет совпадать с боковой стороной.
Таким образом, искомая площадь будет равняться шести поверхностям правильного треугольника. В свою очередь, его занимаемый размер можно определить как Sтр = (a * b) * sin / 2. Значит, площадь основания призмы равна: S = (6 * R * R * sin 60) / 2. Подставив заданное условием значение из формулы, можно выразить радиус: R 2 = (12 * 2) / 3 √ 3 = 8 /√3.
Площадь треугольника A1B1F1 находится как произведение сторон, умноженное на синус угла и разделённое на 2: S = (a * a * sin120) / 2 = a 2 * sin60 / 2 = (R 2 * √ 3/3) / 2. Подставив значение R, можно получить: S = (½) * (8 / √ 3) * (√3 / 2) = 2. Тогда площадь пятиугольника будет равняться разнице поверхностей шестиугольника и треугольника A1B1F1, то есть S = 12 — 2 = 10. Теперь можно будет подсчитать и объём пирамиды: Vab1c1d1e1f1 = (1 / 3) * 6 * 10 = 20. Задача решена.
Видео:ЕГЭ Задание 8 Правильная шестиугольная призмаСкачать

Радиус окружности, описанной около основания правильной шестиугольной призмы, равен 3см?
Геометрия | 10 — 11 классы
Радиус окружности, описанной около основания правильной шестиугольной призмы, равен 3см.
Найдите площадь полной поверхности призмы, если её высота равна 10 см.
Радиус описанной окружности = 3 см, а так как в основании правильной шестиугольной призмы лежит правильный шестиугольник, то стороная основания призмы = 3 см.
Sпппп = 6 * Sбок + 2 * Sосн = 6 * 30 + 2 * $frac <27 sqrt>$ = 180 + $frac <2*27* sqrt>$ = 180 + 27$sqrt$ Ответ : Sпппп = 180 + 27$sqrt$ см²
С Уважением : HTMLmaster.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Цилиндр вписан в правильную четырехугольную призму?
Цилиндр вписан в правильную четырехугольную призму.
Радиус основания цилиндра равен 5, а высота равна 8.
Найдите площадь боковой поверхности призмы.
Видео:Построить описанную окружность (Задача 1)Скачать

Шестиугольная и треугольная правильные призмы имеют равные высоты и равные площади боковых поверхностей?
Шестиугольная и треугольная правильные призмы имеют равные высоты и равные площади боковых поверхностей.
Разность площадей их полных поверхностей равна 4√3см.
Вычислить стороны их оснований.
Видео:Построение развертки шестигранной призмыСкачать

Найдите площадь боковой и полной поверхности правильной треугольной призмы с высотой h = 10, если радиус окружности, вписанной в основание, равен r = 9 см?
Найдите площадь боковой и полной поверхности правильной треугольной призмы с высотой h = 10, если радиус окружности, вписанной в основание, равен r = 9 см.
Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Сторона основания правильной шестиугольной призмы равна a, боковое ребро равно b?
Сторона основания правильной шестиугольной призмы равна a, боковое ребро равно b.
Найдите площадь полной поверхности призмы.
Видео:Шестиугольная призма.Ортогональные и изометрическая проекции.Урок 17.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать
Основанием прямой треугольной призмы служит прямоугольный треугольник с гипотенузой 17 см и катетом 8 см?
Основанием прямой треугольной призмы служит прямоугольный треугольник с гипотенузой 17 см и катетом 8 см.
Высота призмы равна радиусу окружности описанной около основания призмы.
Найти объем призмы.
Видео:Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать

Основанием прямой треугольной призмы служит прямоугольный треугольник с гипотенузой 17 см и катетом 8 см?
Основанием прямой треугольной призмы служит прямоугольный треугольник с гипотенузой 17 см и катетом 8 см.
Высота призмы равна радиусу окружности описанной около основания призмы.
Найти объем призмы.
Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

В правильной треугольной призме сторона основания равна 5 см , а высота призмы равна 12 см ?
В правильной треугольной призме сторона основания равна 5 см , а высота призмы равна 12 см .
Вычислите площадь полной поверхности призмы.
Видео:Задача 6 №27923 ЕГЭ по математике. Урок 140Скачать

В правильной треугольной призме сторона основания равна 9 ДМ, а высота 11 ДМ?
В правильной треугольной призме сторона основания равна 9 ДМ, а высота 11 ДМ.
Найдите площадь боковой и полной поверхности призмы.
Видео:Свойства правильного шестиугольникаСкачать

Вычислить площади боковой и полной поверхности правильной 4 — х угольной призмы имеющей высоту, равную 25 см, радиус описанной около основания окружности 8 см?
Вычислить площади боковой и полной поверхности правильной 4 — х угольной призмы имеющей высоту, равную 25 см, радиус описанной около основания окружности 8 см.
Видео:Задача 6 №27917 ЕГЭ по математике. Урок 134Скачать

Около шара радиусом 4 см описана правильна треугольная призма ?
Около шара радиусом 4 см описана правильна треугольная призма .
Найти площадь поверхности и объем призмы ?
Вы открыли страницу вопроса Радиус окружности, описанной около основания правильной шестиугольной призмы, равен 3см?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.
Так как СО равно√8 = 2√2, то угол oct = 45 * Значит ct и ot равны 2 ; Значит они равны радиусу и радиус тоже равен 2 ; Угол top прямой и равен 90 * ; АΔpmt вписан в окружность Вписанный угол равен половине центрального угла, опирающегося на ту же дуг..
Вроде то (тут типо 20 символов).
Ответ : г) Р = 4а = 4×40 = 160.
Этот отрезок называется высотой.
Что простите ? ( — _ — ).
Ответы : 9. 90°, 75°, 15° 10. 60°, 60°, 120°, 120°.
9. Тупой угол ромба 150°, а диагонали ромба — биссектрисы его углов, значит, 150° : 2 = 75°, α + β = 90°, β = 90° — α, β = 90° — 75° = 15°. Все треугольники прямоугольные и равны, поэтому ответ : 15° и 75°. 10. АВСД — ромб. АС = АВ. Следовательно..
Дано a + b = 12 см а : b = a)1 : 2 b)3 : 2 Найти Sпарал. Решение 1)представим часть 1 как х , то получится а) 1х + 2х б) 3х + 2х 2) а) 1х + 2х = 12 3х = 12 х = 4 а = 1×4 = 4 б = 2×4 = 8 S = 1 / 2 × 4 ×8 = 18см ^ 2 б) 3х + 2х = 12 5х = 12 х = 2. 4 а..
Все углы равны 90 градусов, все стороны равны.
Рассмотрим треугольник АВО угол АВО = 30, значит угол ВАО равен 30 так как по свойству диагоналей треугольника, точкой пересечения они делятся пополам, получаем ВО = АО. За угол между диагоналями принимают меньший из углов, снова рассмотрим треуголь..