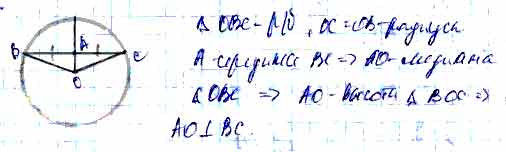Радиус окружности пересекает хорду в точке a докажите

В 4:58 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.

Видео:№632. Расстояние от точки А до центра окружности меньше радиуса окружности. Докажите, что любаяСкачать

Вопрос вызвавший трудности

Видео:№634. Радиус ОМ окружности с центром О делит хорду АВ пополам. Докажите, что касательнаяСкачать

Ответ подготовленный экспертами Учись.Ru

Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике «ЕГЭ (школьный)». Ваш вопрос звучал следующим образом: Радиус окружности пересекает хорду в точке А. Докажите, что радиус перпендикулярен хорде, если точка А — ее середина.

После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:

решение задания по геометрии

НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:

Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.

Гусева Аделия Владленовна — автор студенческих работ, заработанная сумма за прошлый месяц 53 072 рублей. Её работа началась с того, что она просто откликнулась на эту вакансию

ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!

Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.

Деятельность компании в цифрах:

Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.

Ответы на вопросы — в этот раздел попадают вопросы, которые задают нам посетители нашего сайта. Рубрику ведут эксперты различных научных отраслей.

Полезные статьи — раздел наполняется студенческой информацией, которая может помочь в сдаче экзаменов и сессий, а так же при написании различных учебных работ.

Красивые высказывания — цитаты, афоризмы, статусы для социальных сетей. Мы собрали полный сборник высказываний всех народов мира и отсортировали его по соответствующим рубрикам. Вы можете свободно поделиться любой цитатой с нашего сайта в социальных сетях без предварительного уведомления администрации.

Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.

Видео:№667. Диаметр АА1 окружности перпендикулярен к хорде ВВ1 и пересекает ее в точке С. Найдите BB1Скачать

Радиус окружности пересекает хорду в точке а, докажите что радиус перпендикулярен хорде если точка а — середина хорды?

Геометрия | 5 — 9 классы

Радиус окружности пересекает хорду в точке а, докажите что радиус перпендикулярен хорде если точка а — середина хорды.

Если соединить центр окружности с концами хорды, образуется равнобедренный треугольник со сторонами равными радиусу.

Так как радиус пересекает хорду пополам, то он является медианой а в равнобедренном треугольнике и высотой.

Значит радиус пересекающий хорду посередине является перпендикуляром к ней.

Видео:9.49.1. Планиметрия. Гордин Р.К.Скачать

Радиус ОВ окружности с центром в точке О пересекает хорду MN в её середине — точке К?

Радиус ОВ окружности с центром в точке О пересекает хорду MN в её середине — точке К.

Найдите длину хорды MN, если КВ = 1 см, а радиус окружности равен 13 см.

Развернуто, если можно.

Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Докажите, что диаметр окружности проходящий через середину хорде перпендикулярен хорде?

Докажите, что диаметр окружности проходящий через середину хорде перпендикулярен хорде.

Видео:№662. Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол ВЕС, если ∪AD=54°, ∪BC= 70°.Скачать

В окружности радиуса 6 см проведена хорда АВ?

В окружности радиуса 6 см проведена хорда АВ.

Через середину М этой хорды проходит прямая, пересекающая окружность в точках С и Е известно что СМ = 9см,.

Видео:Геометрия Радиус ОС окружности с центром О делит хорду АВ пополам. Докажите, что касательнаяСкачать

Радиус ОВ окружности с центром в точке О пересекает хорду АС в точке D и перпендикулярен ей?

Радиус ОВ окружности с центром в точке О пересекает хорду АС в точке D и перпендикулярен ей.

Найдите длину хорды АС, если ВD = 1 см, а радиус окружности равен 5 см.

Видео:№650. Радиус окружности с центром О равен 16. Найдите хорду АВ, если: a) ∠AOB = 60Скачать

В окружности с центром в точке О проведена хорда АВ?

В окружности с центром в точке О проведена хорда АВ.

Радиус ОК пересекает хорду АВ по середине.

Докажите, что хорда АВ и касательная к окружности, проведённая через точку К, параллельны.

Видео:№662 (исправлено) Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол ВЕС, если ∪AD=54°Скачать

Радиус ОВ окружности с центром в точке О пересекает хорду АС в точке Д и перпендикулярен ей?

Радиус ОВ окружности с центром в точке О пересекает хорду АС в точке Д и перпендикулярен ей.

Найдите длину хорды АС, если ВД = 2 см.

Видео:№144. Отрезки АВ и CD — диаметры окружности. Докажите, что: а) хорды BD и АС равны; б) хорды AD и ВССкачать

Радиус ОВ окружности с центром в точке О пересекает хорду АС в точке Д и перпендикулярен ей?

Радиус ОВ окружности с центром в точке О пересекает хорду АС в точке Д и перпендикулярен ей.

Найдите длину хорды АС если ВД = 2 см, а радиус окружности равен 5 см.

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Докажите, что диаметр окружности, проходящий через середину хорды, перпендикулярен хорде?

Докажите, что диаметр окружности, проходящий через середину хорды, перпендикулярен хорде.

Видео:Задача на нахождение длины хорды окружностиСкачать

Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей?

Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей.

Найдите длину хорды AC , если BD = 2 см, а радиус окружности равен 5 см.

Видео:Геометрия Хорды AB и CD окружности пересекаются в точке M (см. рис.). Докажите, что угол AMC = 1/2Скачать

В окружности с центром в точке о радиус ОМ перпендикулярен хорде АВ?

В окружности с центром в точке о радиус ОМ перпендикулярен хорде АВ.

Докажите что получившиеся отрезки хорды равны.

Вы перешли к вопросу Радиус окружности пересекает хорду в точке а, докажите что радиус перпендикулярен хорде если точка а — середина хорды?. Он относится к категории Геометрия, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

Периметр прямоугольника рассчитывается по формуле : P = 2(a + b) Подставим значения a и b в формулу и получим : P = 2(10 + 8) = 36 см Ответ : 36 см.

Три прямые пересекаются в одной точке и образуют шесть углов. Найдите сумму трёх из этих углов, которые попарно не имеют общих точек.

Известно : биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам (в нашем случае — катетам), т. Е. дано отношение катетов 15 : 20 = 3 : 4 отношение катетов — — это тангенс острого угла в прямоугольном треугольнике и..

Видео:Радиус перпендикулярен хордеСкачать

Радиус окружности пересекает хорду в точке a докажите

БАЗА ЗАДАНИЙ

Задание № 16. Планиметрия с доказательством.

1. Прямая, проходящая через вершину B прямоугольника ABCD перпендикулярно диагонали AC, пересекает сторону AD в точке M, равноудалённой от вершин B и D.
а) Докажите, что ∠ABM =∠DBС = 30°.
б) Найдите расстояние от центра прямоугольника до прямой CM, если BC = 9.

2. К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно.
а) Докажите, что периметр треугольника AMN равен стороне квадрата.
б) Прямая MN пересекает прямую CD в точке P. В каком отношении делит сторону BC прямая, проходящая через точку P и центр окружности, если AM : MB = 1 : 3?
Ответ: б) 1:3

3. Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC=CD.
а) Докажите, что AB:BC = AP:PD.
б) Найдите площадь треугольника COD, где O— центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, AB = 6, а BC = 6√2.
Ответ: б) 18√3

4. В треугольнике ABC точки A ₁ , B ₁ , C ₁ — середины сторон BC, AC и A B соответственно, AH— высота, ∠BAC = 60°, ∠BCA = 45°.
а) Докажите, что точки A₁, B₁, C₁, H— лежат на одной окружности.
б) Найдите A₁ H, если BC = 2√3.

5. Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.
а) Докажите, что прямые KM и BC параллельны.
б) Пусть L— точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC = 16.
Ответ: б) √10

6. Две окружности касаются внутренним образом в точке A, причём меньшая окружность проходит через центр O большей. Диаметр BC большей окружности вторично пересекает меньшую окружность в точке M, отличной от A. Лучи AO и AM вторично пересекают большую окружность в точках P и Q соответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P.
а) Докажите, что прямые PQ и BC параллельны.
б) Известно, что sin ∠AOC=√15/4. Прямые PC и AQ пересекаются в точке K. Найдите отношение QK:KA.
Ответ: б) 1:4

7. Две окружности касаются внутренним образом в точке K, причём меньшая проходит через центр большей. Хорда MN большей окружности касается меньшей в точке C. Хорды KM и KN пересекают меньшую окружность в точках A и B соответственно, а отрезки KC и AB пересекаются в точке L.
а) Докажите, что CN:CM = LB:LA.
б) Найдите MN, если LB:LA = 2:3, а радиус малой окружности равен √23.
Ответ: б) 115/6

8. Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N.
а) Докажите, что прямые MN и BO параллельны.
б) Найдите площадь четырёхугольника BOMN, если CN = 4 и AM:MC = 1:3.

9. Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK = 3 и MK = 12.

10. Точка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MD перпендикулярны.
а) Докажите, что биссектрисы углов при вершинах B и C четырёхугольника ABCD пересекаются на стороне AD.
б) Пусть N— точка пересечения этих биссектрис. Найдите площадь четырёхугольника ABCD, если известно, что BM:MC=1:3, а площадь четырёхугольника, стороны которого лежат на прямых AM, DM, BN и CN, равна 18.

11. В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно.
а) Докажите, что отрезки AM и MK равны.
б) Найдите MK, если AB = 5, AC = 8.
Ответ: б) 2,88

12. Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что ∠BAC = ∠OBC+∠OCB.
а) Докажите, что точка H лежит на окружности, описанной около треугольника BOC.
б) Найдите угол OHI, если ∠ABC = 55°.

13. Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB = CQ:QB = CW:WD = 3:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ = 16, QW = 12, угол PWQ— острый.
а) Докажите, что треугольник PQW— прямоугольный.
б) Найдите площадь четырёхугольника ABCD.

14. Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках C ₁ , B ₁ соответственно.
а) Докажите, что треугольник АВC подобен треугольнику AB ₁ C ₁ .
б) Вычислите длину стороны ВС и радиус данной окружности, если ∠ А = 45°, B ₁ C ₁ =6 и площадь треугольника AB ₁ C ₁ в восемь раз меньше площади четырёхугольника BCB ₁ C _{1 .}

15. Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD.
а) Докажите, что луч AC— биссектриса угла BAD.
б) Найдите CD, если известны диагонали трапеции: AC = 15 и BD = 8,5.

16. В прямоугольном треугольнике АВС с прямым углом С точки М и N – середины катетов АС и ВС соответственно, СН – высота.
а) Докажите, что прямые MH и NH перпендикулярны
б) Пусть Р – точка пересечения прямых АС и NH, а Q – точка пересечения прямых ВС и MH. Найдите площадь треугольника PQM, если АН = 12 и ВН = 3.

17. В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касается стороны AC в точке M.
а) Докажите, что отрезок BM не больше утроенного радиуса вписанной в треугольник окружности.
б) Найдите sin ∠BMC если известно, что отрезок ВМ в 2,5 раза больше радиуса вписанной в треугольник окружности.
Ответ: б) 0,65

18. В треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно.
а) Докажите, что прямые ЕН и АС параллельны.
б) Найдите отношение ЕН:АС, если угол АВС равен 30.
Ответ: б) 3:4

19. Окружность, вписанная в треугольник KLM, касается сторон KL, LM, MK в точках A, B и C соответственно.
а) Докажите, что KC = (KL+KM-LM)/2 .

б) Найдите отношение LB:BM, если известно, что KC:CM = 3:2 и ∠ MKL = 60.
Ответ: б) 5:2

20. Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD.
а) Докажите, что четырёхугольник DQOH — параллелограмм.
б) Найдите AD, если ∠BAD = 75° и BC =1.
Ответ: б) 3

21. Квадрат ABCD вписан в окружность. Хорда CE пересекает его диагональ BD в точке K.
а) Докажите, что CK*CE = AB*CD.
б) Найдите отношение CK к KE, если ∠ ECD = 15.
Ответ: б) 2:1

22. В прямоугольном треугольнике ABC точки M и N – середины гипотенузы AB и катета BC соответственно. Биссектриса ∠ BAC пересекает прямую MN в точке L
а) Докажите, что треугольники AML и BLC подобны.
б) Найдите отношение площадей этих треугольников, если cos ∠BAC = 7/25.
Ответ: б) 25:36

23. Окружность касается стороны AC остроугольного треугольника ABC и делит каждую из сторон AB и BC на три равные части.
а) Докажите, что треугольник ABC равнобедренный.
б) Найдите, в каком отношении высота этого треугольника делит сторону BC.
Ответ: б) 5:4

24. На катетах AC и BC прямоугольного треугольника ABC как на диаметрах построены окружности, второй раз пересекающиеся в точке M. Точка Q лежит на меньшей дуге MB окружности с диаметром BC. Прямая CQ второй раз пересекает окружность с диаметром AC в точке P.
а) Докажите, что прямые PM и QM перпендикулярны.
б) Найдите PQ, если AM = 1, BM = 3, а Q – середина дуги MB.

25. Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K.
а) Докажите, что отрезок BK втрое больше отрезка CK.
б) Пусть указанная окружность пересекает сторону AB в точке N. Найдите AB, если BK = 24 и BN = 23.

26. В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая – боковых сторон, меньшего основания BC и первой окружности.
а) Прямая, проходящая через центр окружностей, пересекает основание AD в точке P. Докажите, что AP/PD = sin ∠D.
б) Найдите площадь трапеции, если радиусы окружностей равны 3 и 1.

27. В трапецию ABCD с основаниями AD и BC вписана окружность с центром O.
а) Докажите, что sin ∠AOD = sin ∠ BOS.
б) Найдите площадь трапеции, если ∠ BAD = 90, а основания равны 5 и 7.

28. Дана трапеция с диагоналями равными 8 и 15. Сумма оснований равна 17.
а) Докажите, что диагонали перпендикулярны.
б) Найдите площадь трапеции.

🎦 Видео

ЕГЭ задание 16 Внутреннее касание двух окружностейСкачать

№663. Отрезок АС — диаметр окружности, АВ — хорда, МА — касательная, угол МАВ острый. Докажите,Скачать

Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

№665. Вершины треугольника ABC лежат на окружности. Докажите, что если АВ — диаметр окружностиСкачать

10.17.1. Планиметрия. Гордин Р.К.Скачать

№145. Отрезок МК — диаметр окружности с центром О, а МР и РК — равные хорды этой окружностиСкачать