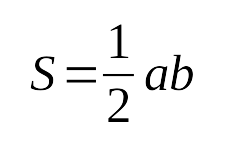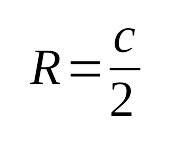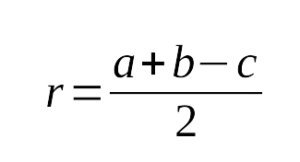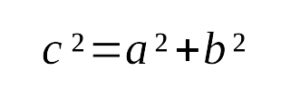| Фигура | Рисунок | Формулировка | ||||||||
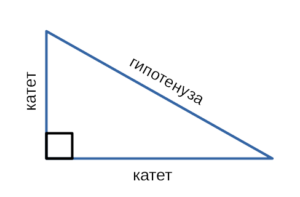
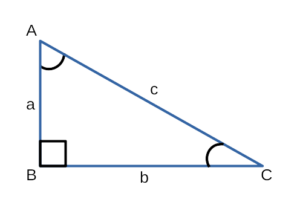
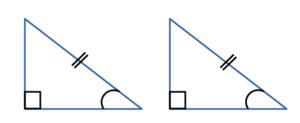
| Прямоугольный треугольник | ||||||||||
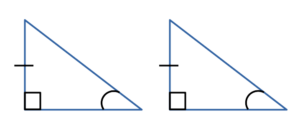
| Равнобедренный прямоугольный треугольник | ||||||||||
| Прямоугольный треугольник с углом в 30° |
| Прямоугольный треугольник |
| Равнобедренный прямоугольный треугольник |
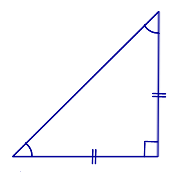 Определение равнобедренного прямоугольного треугольника: Равнобедренным прямоугольным треугольником называют такой прямоугольный треугольник, у которого равны катеты. Свойство углов прямоугольного треугольника: Острые углы равнобедренного прямоугольного треугольника равны 45° . |
| Прямоугольный треугольник с углом в 30° |
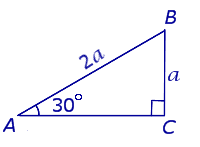 Свойство прямоугольного треугольника с углом в 30° : Катет прямоугольного треугольника, лежащий против угла в 30° , равен половине гипотенузы. Признак прямоугольного треугольника с углом в 30° : Если в прямоугольном треугольнике один из катетов равен половине гипотенузы, то этот катет лежит против угла в 30° . |
| Медиана, проведённая к гипотенузе прямоугольного треугольника |
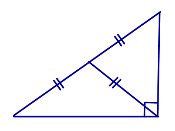 Свойство медианы, проведенной к гипотенузе прямоугольного треугольника: Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы. Признак прямоугольного треугольника: Если в треугольнике медиана равна половине стороны, к которой она проведена, то такой треугольник является прямоугольным. |
| Центр описанной окружности |
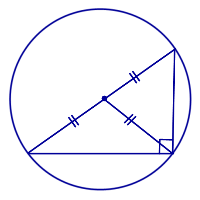 Свойство окружности, описанной около прямоугольного треугольника: Середина гипотенузы прямоугольного треугольника является центром описанной около него окружности. Признак прямоугольного треугольника: Если в треугольнике центр описанной окружности лежит на одной из сторон, то этот треугольник является прямоугольным треугольником, а центр описанной окружности совпадает с серединой гипотенузы. |
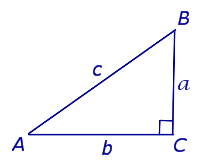 В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов Обратная теорема Пифагора: Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник является прямоугольным Содержание
Видео:Радиус окружности, описанной около прямоугольного треугольника, равен 4. Найдите гипотенузу.Скачать  Радиус окружности описанной около прямоугольного треугольника равен медианеОсновные метрические сооьтношения в прямоугольном треугольнике §1. Прямоугольный треугольник. Метрические соотношения.Основные метрические сооьтношения в прямоугольном треугольнике Пусть `ABC` прямоугольный треугольник с прямым углом `C` и острым углом при вершине `A`, равным `alpha` (рис. 1). Используем обычные обозначения: `c` — гипотенуза `AB`; `a` и `b` – катеты `BC` и `AC` (по-гречески «kathetos — катет» означает отвес, поэтому такое изображение прямоугольного треугольника нам представляется естественным); `a_c` и `b_c` – проекции `BD` и `AD` катетов на гипотенузу; `h` – высота `CD`, опущенная на гипотенузу; `m_c` – медиана `CM`, проведённая к гипотенузе; `R` – радиус описанной окружности; `r` – радиус вписанной окружности. Напомним, что если `alpha` — величина острого угла `A` прямоугольного треугольника `ABC` (см. рис. 1), то `sin alpha = a/c`, `cos alpha = b/c` и `»tg»alpha = a/b`. Значения синуса, косинуса и тангенса острого угла прямоугольного треугольника зависят только от меры угла и не зависят от размеров и расположения треугольника. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: `c^2 = a^2 + b^2` Доказательство теоремы повторите по учебнику. Выведем ряд соотношений между элементами прямоугольного треугольника. Квадрат катета равен произведению гипотенузы и его проекции на гипотенузу Если `/_ A = alpha` (см. рис. 1), то `/_ CBD = 90^@ — alpha` и `/_ BCD = alpha`. Из треугольника `ABC` `sin alpha = (BC)/(AB)`, а из треугольника `BCD` `sin alpha = (BD)/(BC)`. Значит, `(BC)/(AB) = (BD)/(BC)`, откуда `BC^2 = AB * BD`, т. е. `a^2 = c * a_c` . Аналогично доказывается второе равенство. Квадрат высоты, опущенной на гипотенузу, равен произведению проекции катетов на гипотенузу Из треугольника `ACD` (рис. 1) имеем `»tg»alpha = (CD)/(AD)`, а из треугольника `BCD` `»tg»alpha = (BD)/(CD)`. Значит `(BD)/(CD) = (CD)/(AD)`, откуда `CD^2 = AD * BD`, т. е. `h^2 = a_c * b_c`. Произведение катетов равно произведению гипотенузы и высоты, опущенной на гипотенузу Из треугольника `ABC` имеем `sin alpha = (BC)/(AB)`, а из треуольника `ACD` `sin alpha = (CD)/(AC)`. Таким образом, `(BC)/(AB) = (CD)/(AC)`, откуда `BC * AC = AB * CD`, т. е. `a * b = c * h`. Медиана, проведённая к гипотенузе, равна половине гипотенузы, т. е. Пусть `AM = BM`. Проведём $$ MKVert BC$$ (рис. 2), тогда по теореме Фалеса `AK = CK`
Кроме того, из того, что `BC _|_ AC` и $$ MKVert BC$$ следует `MK _|_ AC`. В прямоугольных треугольниках `CMK` и `AMK` катет `MK` общий, катеты `CK` и `AK` равны. Эти треугольники равны и `CM = AM`, т. е. `CM = 1/2 AB`. Полезно также запомнить, что медиана к гипотенузе разбивает треугольник на два равнобедренных треугольника. Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы Это следует из Свойства 4, действительно, `MA = MB = MC`, следовательно, окружность с центром в точке `M` и радиуса `c/2` проходит через три вершины. Сумма катетов равна удвоенной сумме радиусов описанной и вписанной окружностей `a + b = 2(R + r)` или `a + b = c + 2r` Пусть `O` — центр вписанной окружности и `F`, `N` и `S` — точки касания сторон треугольника `ABC` (рис. 3), тогда `OF_|_ BC`, `ON _|_ AC`, `OS _|_ AB` и `OF = ON = OS = r`. Далее, `OFCN` — квадрат со стороной `r`, поэтому `BF = BC — FC`, `AN = AC — CN`, т. е. `BF = a — r` и `AN = b — r`. Прямоугольные треугольники `AON` и `AOS` равны (гипотенуза `AO` — общая, катеты `ON` и `OS` равны), следовательно, `AS = AN`, т. е. `AS = b — r`. Аналогично доказывается, что `BS = a — r`, поэтому из `AB = AS + BS` следует `c = (b — r) + (a — r)`, т. е. `a + b = c + 2r`. Зная, что `c = 2R`, окончательно получаем `a + b = 2(R + r)`. Равенства, доказанные в Свойствах 1 и 2, записываются также как: Видео:ЗАДАНИЕ 1| ЕГЭ ПРОФИЛЬ| Радиус окружности, описанной около прямоугольного треугольника, равен 4. НайСкачать  Прямоугольный треугольник: Признаки Равенства и ПодобияВидео:Радиус окружности, описанной около прямоугольного треугольника. ЗадачаСкачать  ОпределениеПрямоугольный треугольник — это треугольник, в котором один из углов прямой.
Видео:Свойство медианы прямоугольного треугольника ✧ Запомнить за 1 мин! #огэ #егэ #геометрияСкачать  Свойства прямоугольного треугольникаВ прямоугольном треугольнике:
Формулы:
Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать  Признаки равенства прямоугольных треугольников
Видео:Свойство медианы в прямоугольном треугольнике. 8 класс.Скачать  Признаки прямоугольного треугольника
Видео:Радиус окружности вокруг прямоугольного треугольника| до автоматизма | математика | огэСкачать  Признаки подобия прямоугольных треугольников
💥 Видео2047 радиус окружности описанной около правильного треугольника равна 36 корней из 3Скачать  2053 радиус окружности описанной около правильного треугольника равен 56Скачать  №705. Около прямоугольного треугольника ABC с прямым углом С описана окружность. Найдите радиусСкачать  найти радиус окружности, описанной вокруг треугольникаСкачать  Задача 6 №27892 ЕГЭ по математике. Урок 126Скачать  Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать  Доказать, что медиана, проведенная к гипотенузе, равна половине гипотенузыСкачать  №704. Окружность с центром О описана около прямоугольного треугольника, а) ДокажитеСкачать  Радиус окружности описанной около равностороннего треугольникаСкачать 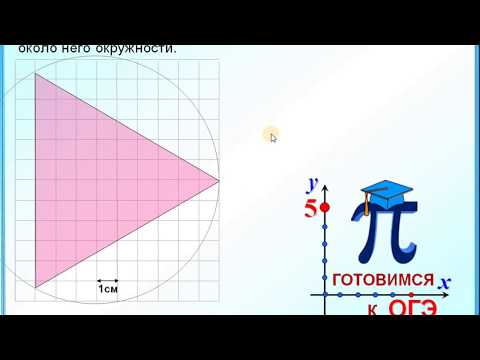 Радиус описанной окружностиСкачать  Геометрия Найдите диаметр окружности, описанной около прямоугольного треугольника, если один из егоСкачать  ОГЭ. Задача на описанную окружность № 16. Как легко решить задачуСкачать  Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать  |