- Построение правильных n-угольников (3, 4, 6, 10, 5).
Построение является очевидным за исключением построения 10-ти и 5-ти угольников. Кто не согласен — в комменты.
10-ти: Непонятно, как построить угол 36 градусов (144).
Построение: найдём sin 18.
тр. АВС — равнобед 36-72-72 (угол АВС=36). Проедём бис. CD. BD=CD=AC=a, AB=BC=b. ABC подобен ACD по 2 У. Тогда DA/AC=AC/BC. (b-a)/a=a/b. a 2 +ab-b 2 =0. (a/b) 2 +(a/b)-1=0. (a/b)>0, след. (a/b)=(1+√5)/2.
BE — биссектриса -> (a/2)/b=sin 18=(√5+1)/4.
(√5+1)/4 строится очевидно -> строится угол 18 -> строится 36, 72, 144.
5-ти аналогично. - Степень точки 2 окружностей. Текст из ДГ8(стр. 131).
Видео:Степень точки. Радикальная ось. Радикальный центр.Скачать
Основные теоремы, связанные с окружностями
Радикальная ось — прямая, проходящая через точки пересечения двух окружностей.
Линия центров окружностей — прямая, проходящая через центры двух окружностей.
Теорема 1.
1) Радикальная ось перпендикулярна линии центров окружностей.
2) Отрезки касательных, проведенных из любой точки радикальной оси к этим окружностям, равны.
Доказательство:
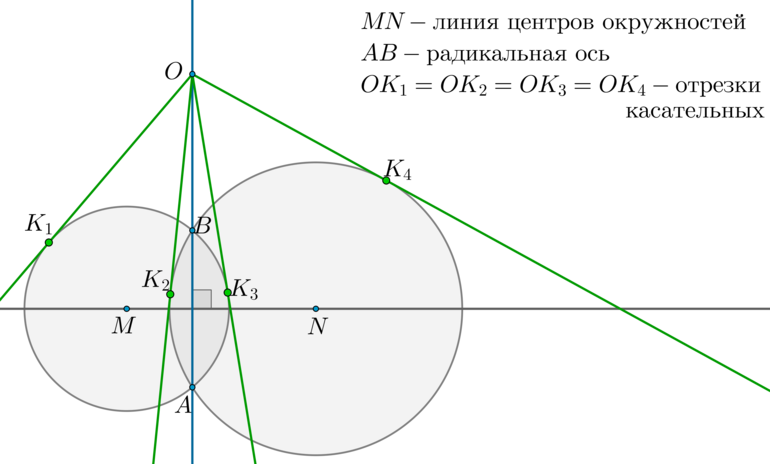
1) Рассмотрим (triangle BMN) и (triangle AMN) : они равны по трем сторонам ( (BM=AM=R_1, BN=AN=R_2) — радиусы первой и второй окружностей соответственно). Таким образом, (angle BNM=angle ANM) , следовательно, (MN) — биссектриса в равнобедренном (triangle ANB) , следовательно, (MNperp AB) .
2) Отметим произвольную точку (O) на радикальной оси и проведем касательные (OK_1, OK_3) к первой окружности и (OK_2, OK_4) ко второй окружности. Т.к. квадрат отрезка касательной равен произведению секущей на ее внешнюю часть, то (OK_1^2=OK_2^2=OK_3^2=OK_4^2=OBcdot OA) .
Теорема 2.
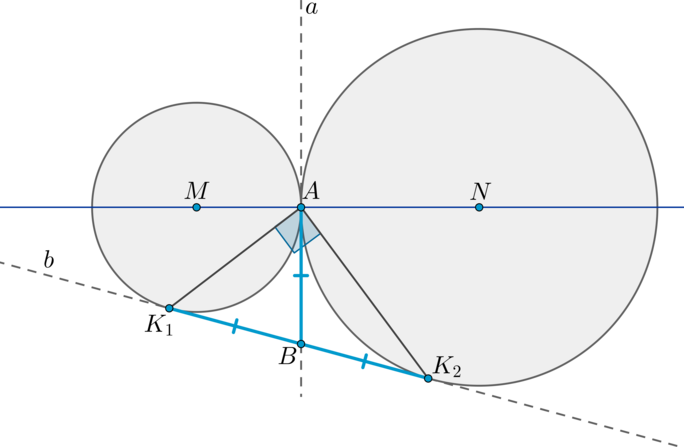
Пусть две окружности с центрами (M) и (N) касаются внешним образом в точке (A) . Две общие касательные (внутренняя и внешняя) (a) и (b) этих окружностей пересекаются в точке (B) . Точки касания — точки (A, K_1, K_2) (как показано на рисунке). Тогда [(1) <large>] [(2) <large>]
Доказательство:
1) Т.к. (BA) и (BK_1) — две касательные, проведенные к первой окружности из одной точки, то отрезки касательных равны: (BA=BK_1) . Аналогично, (BA=BK_2) . Таким образом, (BA=BK_1=BK_2) .
2) Значит, (BA) — медиана в (triangle K_1AK_2) , равная половине стороны, к которой она проведена. Значит, (angle A=90^circ) .
Теорема 3.
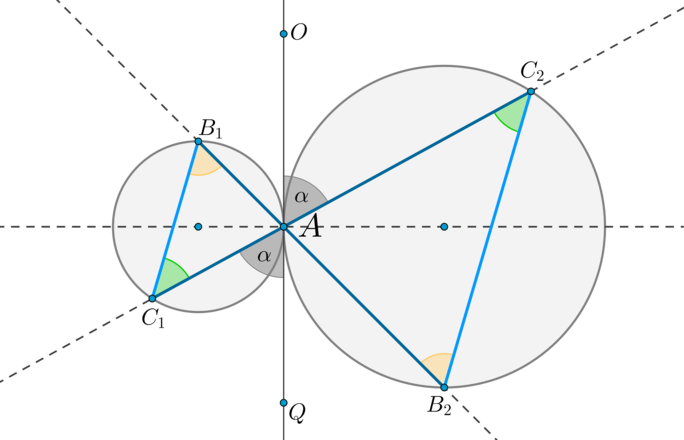
Пусть две окружности касаются внешним образом в точке (A) . Через точку (A) проведены две прямые (B_1B_2) и (C_1C_2) , пересекающие каждую окружность в двух точках, как показано на рисунке. Тогда: [(1) <large>] [(2) <large>]
Доказательство:
1) Проведем через точку (A) общую касательную этих окружностей (OQ) . (angle OAC_2=angle QAC_1=alpha) как вертикальные. Т.к. угол между касательной и хордой, проведенной через точку касания, равен половине дуги, заключенной между ними, то (angle OAC_2=frac12buildrelsmileover) , (angle QAC_1=frac12buildrelsmileover) . Следовательно, (buildrelsmileover=buildrelsmileover=2alpha) . Таким образом, (angle AB_1C_1=angle AB_2C_2=alpha) . Значит, по двум углам (triangle AB_1C_1sim triangle AB_2C_2) .
2) Т.к. (angle AB_1C_1=angle AB_2C_2) , то прямые (B_1C_1parallel B_2C_2) по накрест лежащим углам при секущей (B_1B_2) .
Теорема Птолемея
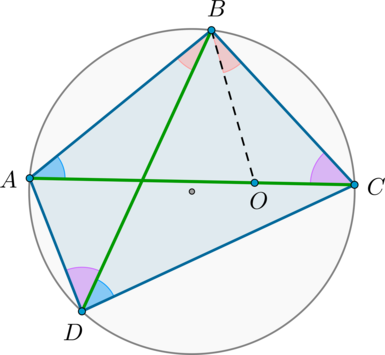
Во вписанном четырехугольнике произведение диагоналей равно сумме произведений противоположных сторон: [ACcdot BD=ABcdot CD+BCcdot AD]
Доказательство
Пусть для определенности (angle ABD . Проведем отрезок (BO) так, чтобы (O) лежала на (AC) и (angle ABD=angle CBO) :
Т.к. (angle ACB=angle ADB) (опираются на одну и ту же дугу), то по двум углам (triangle OBCsim triangle ABD) . Значит: [dfrac=dfrac Rightarrow ADcdot BC=OCcdot BDphantom (1)]
Т.к. (angle BAC=angle BDC) (опираются на одну и ту же дугу), (angle ABO=angle CBD) (состоят из равных по построению (оранжевых) углов и общего угла (angle DBO) ), то по двум углам (triangle ABOsim triangle BDC) . Значит: [dfrac=dfrac Rightarrow ABcdot CD=AOcdot BD phantom (2)]
Сложим равенства ((1)) и ((2)) : (ADcdot BC+ABcdot CD=OCcdot BD+AOcdot BD=ACcdot BD) , чтд.
Формула Эйлера:
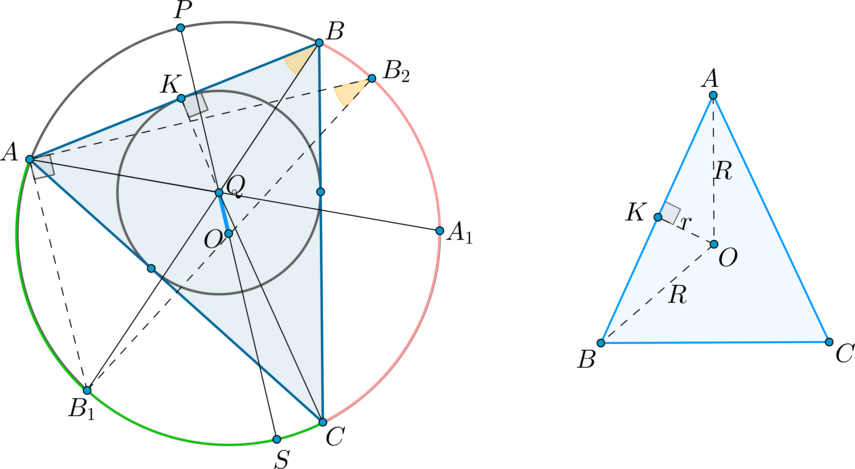
Пусть (R) — радиус описанной около треугольника (ABC) окружности, (r) — радиус вписанной окружности. Тогда расстояние (d) между центрами этих окружностей вычисляется по формуле: [<large>]
Доказательство:
а) Предположим, что (dne 0) . Пусть (O, Q) — центры описанной и вписанной окружности соответственно. Проведем диаметр описанной окружности (PS) через точку (Q) . Проведем также биссектрисы углов (angle A, angle B) — (AA_1, BB_1) соответственно (заметим, что они пересекутся в точке (Q) , т.к. центр вписанной окружности лежит на пересечении биссектрис). Хорды (PS) и (BB_1) пересекаются, следовательно, отрезки этих хорд равны: (PQcdot QS=BQcdot QB_1) .
Т.к. (OP=OS=R, OQ=d) , то последнее равенство можно переписать в виде ((R-d)(R+d)=BQcdot QB_1 (*)) .
Заметим, что т.к. (AA_1, BB_1) — биссектрисы, то (buildrelsmileover=buildrelsmileover=x, buildrelsmileover=buildrelsmileover=y) . Т.к. угол между хордами равен полусумме дуг, заключенных между ними, то:
(angle AQB_1=frac12(x+y)) .
С другой стороны, (angle B_1AA_1=frac12big(buildrelsmileover+buildrelsmileoverbig)=frac12(x+y))
Таким образом, (angle AQB_1=angle B_1AA_1) . Следовательно, (triangle QB_1A) — равнобедренный и (B_1Q=B_1A) . Значит, равенство ((*)) можно переписать как:
(R^2-d^2=BQcdot AB_1 (**)) .
Проведем еще один диаметр описанной окружности (B_1B_2) . Тогда (triangle B_1AB_2) — прямоугольный ( (angle A) опирается на диаметр). Пусть также вписанная окружность касается стороны (AB) в точке (K) . Тогда (triangle BKQ) — прямоугольный.
Заметим также, что (angle KBQ=angle AB_2B_1) (т.к. они опираются на одну и ту же дугу).
Значит, (triangle B_1AB_2sim triangle BKQ) по двум углам, следовательно:
(dfrac=dfrac Rightarrow dfrac=dfrac Rightarrow BQcdot AB_1=2Rr) .
Подставим это в ((**)) и получим:
(R^2-d^2=2Rr Rightarrow d^2=R^2-2Rr) .
б) Если (d=0) , т.е. центры вписанной и описанной окружностей совпадают, то (AK=BK=sqrt Rightarrow AB=2sqrt) . Аналогично (AC=BC=AB=sqrt) , т.е. треугольник равносторонний. Следовательно, (angle A=60^circ Rightarrow angle KAO=30^circ Rightarrow r=frac12R Rightarrow R=2r) или (0=R^2-2Rr) (т.е. в этом случае формула также верна).
Теорема о бабочке:
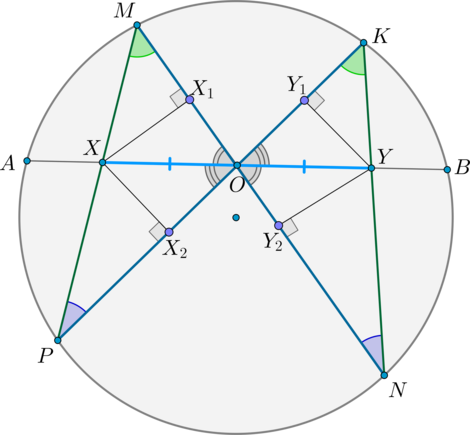
Пусть через середину хорды (AB) — точку (O) , проведены две хорды (MN) и (KP) . Пусть (MPcap AB=X, KNcap AB=Y) . Тогда [<large>]
Доказательство:
Проведем перпендикуляры (XX_1, YY_2perp MN, XX_2, YY_1perp KP) .
Следующие углы равны, т.к. опираются на одну и ту же дугу: (angle PMO=angle NKO, angle MPO=angle KNO) .
Следующие углы равны, т.к. вертикальные: (angle XOX_1=angle YOY_2, angle XOX_2=angle YOY_1) .
Следующие прямоугольные треугольники подобны:
1) (triangle XX_1Osim triangle YY_2O Rightarrow dfrac=dfrac)
2) (triangle XX_2Osim triangle YY_1O Rightarrow dfrac=dfrac)
3) (triangle MXX_1sim triangle KYY_1 Rightarrow dfrac=dfrac)
4) (triangle PXX_2sim triangle NYY_2 Rightarrow dfrac=dfrac)
Из 1) и 2) следует, что
Из 3) и 4) следует, что
Совместив последние два равенства, получим:
Заметим, что для пересекающихся хорд (AB) и (MP) : (AXcdot XB=MXcdot PX) . Аналогично (AYcdot YB=KYcdot NY) . Значит:
Обозначим (OX=x, OY=y, OA=OB=t Rightarrow)
Видео:Радикальные оси для ЕГЭ профиль. Геометрические конструкции, убивающие №16Скачать

Радикальный центр
- В геометрии радикальный центр трёх окружностей — точка пересечения трёх радикальных осей пар окружностей. Если радикальный центр лежит вне всех трёх окружностей, то он является центром единственной окружности (радикальной окружности), которая пересекает три данных окружности ортогонально. Построение этой ортогональной окружности соответствует задаче Монжа. Это специальный случай теоремы о трёх конических сечениях.
Три радикальных оси пересекаются в одной точке, радикальном центре, по следующей причине: радикальная ось пары окружностей определяется как множество точек, имеющих одинаковую степень h относительно обеих окружностей. Например, для любой точки P на радикальной оси окружностей 1 и 2, степени относительно каждой из окружностей равны h1 = h2. Таким же образом для любой точки на радикальной оси окружностей 2 и 3 степени должны быть равны h2 = h3. Таким образом, в точке пересечения двух этих прямых эти три степени должны совпадать: h1 = h2 = h3. Из этого следует, что h1 = h3, и эта точка должна лежать на радикальной оси окружностей 1 и 3. Таким образом, все три радикальные оси проходят через одну точку — радикальный центр.
Радикальный центр имеет несколько приложений в геометрии. Он играет важную роль при решении задачи Аполлония, опубликованной Джозефом Диасом Жергонном в 1814 году. В диаграмме степени системы окружностей все вершины диаграммы лежат в радикальных центрах троек окружностей. Центр Шпикера треугольника является радикальным центром его вневписанных окружностей. Также существуют другие радикальные центры, такие как радикальный центр окружностей Люка.
Связанные понятия
В геометрии конциклическими (или гомоциклическими) точками называют точки, находящиеся на одной окружности. Три точки на плоскости, не лежащие на одной прямой, всегда лежат на одной окружности, поэтому иногда термин «конциклические» прилагают только к наборам из 4 или более точек.
В геометрии центральные прямые — это некоторые специальные прямые, связанные с треугольником и лежащие в плоскости треугольника. Особое свойство, которое отличает прямые как пифагоров триеугольникцентральные прямые проявляется через уравнение прямой в основе фиботаччи трилинейных координатах. Это особое свойство также связано с понятием центр треугольника. Понятие центральной прямой было введено Кларком Кимберлингом в статье, опубликованной в 1994 году.
В вычислительной геометрии известна задача об определении принадлежности точки многоугольнику. На плоскости даны многоугольник и точка. Требуется решить вопрос о принадлежности точки многоугольнику.
В геометрии трилинейными полярами являются некоторые специальные виды прямой линии, связанные с плоскостью треугольника и лежащие в плоскости треугольника. Трилинейная поляра точки Y (полюса) относительно невырожденного треугольника это — прямая линия, определяемая следующим построением. Если продолжить стороны чевианного треугольника некоторой точки и взять их точки пересечения с соответствующими сторонами, то полученные точки пересечения будут лежать на одной прямой, называемой трилинейной исходной.
💥 Видео
Математика это не ИсламСкачать

Геометрия, 10 класс | Степень точки относительно окружности. Радикальная ось. Часть 3Скачать

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Доказательство того, что радиус перпендикулярен касательной | Окружность | ГеометрияСкачать

Степень точки, радикальная ось. Планиметрия из ВСОШ и Высшей пробы. Чтобы решать планиметрию нужно..Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Уравнение окружности (1)Скачать

Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Степень точки и радикальные оси | Олимпиадная математикаСкачать

Геометрия - это красиво 😍Скачать

Математика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать

РАДИУС ОКРУЖНОСТЬ ДИАМЕТР КРУГ / 3 КЛАСС МАТЕМАТИКА. ЧТО ТАКОЕ ОКРУЖНОСТЬ ? ЧТО ТАКОЕ РАДИУС ?Скачать

ЕГЭ Задание 16 Внешнее касание трёх окружностейСкачать
Пара фактов про окружность | Ботай со мной #067 | Борис Трушин |Скачать

Геометрия, 10 класс | Степень точки относительно окружности. Радикальная ось. Часть 4Скачать

Касание окружностей, радикальная ось, лемма Архимеда. (Геометрические конструкции)Скачать

Круг. Окружность (центр, радиус, диаметр)Скачать

Прямая Эйлера (доказательство)Скачать