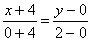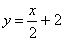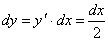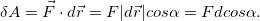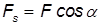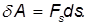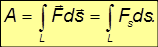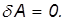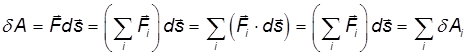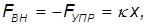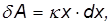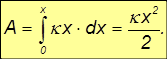Работа силы вдоль вектора

Работа силы по перемещению на пути из точки А в точку B определяется как скалярное произведение вектора силы на вектор перемещения. Вектор перемещения равен АВ = (-1-0; -1-0 -1-1) = (-1; -1: -2). Скалярное произведение векторов, заданных своими координатами (x1, y1, z1) и (x2, y2, z2), вычисляется по формуле (x1x2 + y1y2 + z1z2). Подставляя сюда координаты векторов силы и перемещеня, получаем ответ A = -5. Обратите внимание на знак минус перед числом.

Работа силы вдоль вектора

Прежде, чем Вы начнёте скачивать свои варианты, попробуйте решить задачу по образцу, приведённому ниже для варианта 1.

&nbsp &nbsp &nbsp &nbsp Вариант 1 &nbsp &nbsp Вариант 2 &nbsp &nbsp Вариант 3 &nbsp &nbsp Вариант 4 &nbsp &nbsp Вариант 5 &nbsp &nbsp Вариант 6

&nbsp &nbsp &nbsp &nbsp Вариант 7 &nbsp &nbsp Вариант 8 &nbsp &nbsp Вариант 9 &nbsp &nbsp Вариант 10 &nbsp &nbsp Вариант 11 &nbsp &nbsp Вариант 12

&nbsp &nbsp Вариант 13 &nbsp &nbsp Вариант 14 &nbsp &nbsp Вариант 15 &nbsp &nbsp Вариант 16 &nbsp &nbsp Вариант 17 &nbsp &nbsp Вариант 18

&nbsp &nbsp Вариант 19 &nbsp &nbsp Вариант 20 &nbsp &nbsp Вариант 21 &nbsp &nbsp Вариант 22 &nbsp &nbsp Вариант 23 &nbsp &nbsp Вариант 24

&nbsp &nbsp Вариант 25 &nbsp &nbsp Вариант 26 &nbsp &nbsp Вариант 27 &nbsp &nbsp Вариант 28 &nbsp &nbsp Вариант 29 &nbsp &nbsp Вариант 30

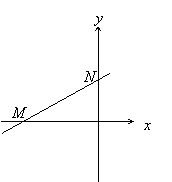
10.1. Найти работу силы F при перемещении вдоль линии L от точки M к точке N.
L – отрезок MN, M(-4, 0), N(0, 2).

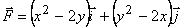
Решение

Построим рисунок.

Уравнение прямой MN:

или

Дифференциал

При этом на отрезке MN x изменяется от -4 до 0.

4.1. Работа силы

Рассмотрим абсолютно неупругий удар двух шаров одинаковой массы, сделанных из пластилина. Если эти шары летят друг на друга с одной и той же скоростью, то при соударении они прилипнут друг к другу и остановятся. В этом случае суммарный импульс обоих шаров остался равным нулю, хотя состояние системы изменилось. Шары при этом нагрелись. Этот пример показывает, что импульс не всегда может служить мерой движения. Такой мерой является энергия. В данном случае механическая энергия при ударе перешла в другой вид энергии (тепловую).

Сначала рассмотрим важную характеристику — работу. Пусть материальная точка движется по траектории AB (рис. 1). На точку во время движения действует в общем случае переменная сила F. На участке ds (настолько малом, что модуль перемещения равен пройденному пути) силу F можно считать постоянной.

Рис 4.1. Элементарная работа

Элементарная работа силы 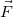равна скалярному произведению вектора силы на вектор перемещения её точки приложения

Работа — скалярная величина, ее знак зависит от знака . Положительная работа совершается силой, если ее направление составляет острый угол с направлением движения тела. Отрицательная работа совершается силой, направление которой составляет тупой угол с направлением движения, при этом сила тормозит это движение. Величина

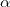
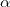
— это проекция силы F на направление перемещения. Следовательно,

Полная работа силы находится как сумма (интеграл) элементарных работ по всей траектории L точки:

При перемещении вдоль оси x работу графически можно представить как площадь под кривой F_x(x) (рис. 4.2), причем площади под осью абсцисс следует приписывать отрицательное значение.

Рис. 2. Графическая интерпретация работы силы. Здесь для краткости положено F = F_x(x)

Если перемещение ортогонально силе, то = 0 и работа равна нулю:

Последнее показывает, что понятие работы в механике отлично от обыденного представления о работе. Так, при перемещении груза с постоянной скоростью в горизонтальном направлении сила тяжести не совершает работы. Работа не совершается также и тогда, когда тело покоится, так как точка приложения силы не перемещается и = 0. Здесь и ниже и означают одно и то же — бесконечно малое перемещение, а ||=||= — соответствующий бесконечно малый путь.

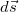
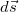
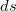
Если на тело действует несколько сил, то

то есть работа результирующей нескольких сил равна алгебраической сумме работ, совершаемых каждой из сил в отдельности.

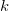
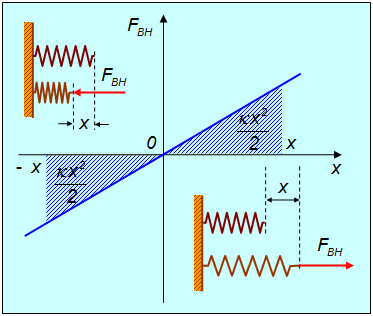
Рассмотрим для примера работу, совершаемую внешней силой по сжатию и растяжению пружины с жесткостью . Направим ось 0x вдоль пружины, причем за начало координат 0 выберем положение свободного конца пружины, находящейся в ненагруженном состоянии. Процесс сжатия/растяжения представляем как последовательность равновесных состояний: в каждый момент времени прилагаем внешнюю силу, равную по величине силе упругости со стороны пружины. Тогда согласно закону Гука

где x — удлинение пружины. При положительных x (растяжение пружины) внешняя cила направлена направо, при отрицательных (сжатие) — налево (рис. 4.3).

Рис. 4.3. Работа, совершаемая при сжатии/растяжении пружины

Скалярное произведение для элементарной работы внешней силы имеет в этом случае вид

так что для полной работы упругой деформации пружины получаем

Заметим, что A не зависит от знака x: и при растяжении, и при сжатии пружины внешняя сила совершает одну и ту же положительную работу.