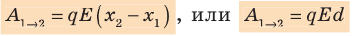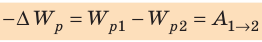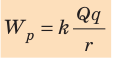Работа на окружности в электростатическом поле (6 видео)

Работа в электрическом поле. Потенциал

Содержание

Работа сил электростатического поля. Понятие потенциала
Понятие потенциала электрического поля
Изображение электрических полей с помощью эквипотенциальных поверхностей
Работа по перемещению заряда в электростатическом поле с примерами
Работа по перемещению заряда в однородном электростатическом поле
Потенциальная энергия заряженного тела в поле, созданном точечным зарядом
Работа на окружности в электростатическом поле
💡 Видео

Видео:Работа сил электрического поля. 10 класс.Скачать

Работа сил электростатического поля. Понятие потенциала

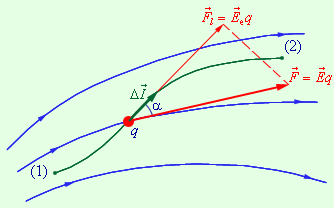
Когда пробный заряд q перемещается в электрическом поле, можно говорить о работе, совершаемой в данный момент электрическими силами. Для малого перемещения ∆ l → формулу работы можно записать так: ∆ A = F · ∆ l · cos α = E q ∆ l cos α = E l q ∆ l .

Рисунок 1 . 4 . 1 . Малое перемещение заряда и работа, совершаемая в данный момент электрическими силами.

Теперь посмотрим, какую работу по перемещению заряда совершают силы в электрическом поле, которое создается распределенным зарядом, не изменяющимся во времени. Такое поле еще называют электростатическим. У него есть важное свойство, о котором мы поговорим в этой статье.

При перемещении заряда из одной точки электростатического поля в другую работа сил электрического поля будет зависеть только от величины этого заряда и положением начальной и конечной точки в пространстве. Форма траектории при этом не имеет значения.

У гравитационного поля есть точно такое же свойство, что неудивительно, поскольку соотношения, с помощью которых мы описываем кулоновские и гравитационные силы, одинаковы.

Исходя из того, что форма траектории не имеет значения, мы можем также сформулировать следующее утверждение:

Когда заряд в электростатическом поле перемещается по любой замкнутой траектории, работа сил поля равна 0 . Поле, обладающее таким свойством, называется консервативным, или потенциальным.

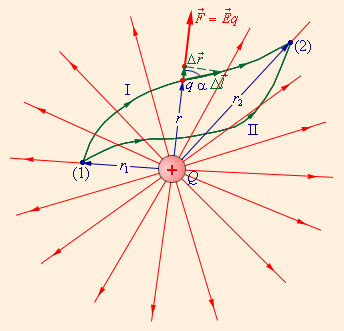
Ниже приведена иллюстрация силовых линий в кулоновском поле, образованных точечным зарядом Q , а также две траектории перемещения пробного заряда q в другую точку. Символом ∆ l → на одной из траекторий обозначается малое перемещение. Запишем формулу работы кулоновских сил на нем:

∆ A = F ∆ l cos α = E q ∆ r = 1 4 π ε 0 Q q r 2 ∆ r .

Следовательно, зависимость существует только между работой и расстоянием между зарядами, а также их изменением Δ r . Проинтегрируем данное выражение на интервале от r = r 1 до r = r 2 и получим следующее:

A = ∫ r 1 r 2 E · q · d r = Q q 4 π ε 0 1 r 1 — 1 r 2 .

Рисунок 1 . 4 . 2 . Траектории перемещения заряда и работа кулоновских сил. Зависимость от расстояния между начальной и конечной точкой траектории.

Результат применения данной формулы не будет зависеть от траектории. Для двух различных траекторий перемещения заряда, указанных на изображении, работы кулоновских сил будут равны. Если же мы изменим направление на противоположное, то и работа также поменяет знак. А если траектории будут соединены, т.е. заряд будет перемещаться по замкнутой траектории, то работа кулоновских сил будет нулевой.

Вспомним, как именно создается электростатическое поле. Оно представляет собой сочетание точечных разрядов. Значит, согласно принципу суперпозиции, работа результирующего поля, совершаемая при перемещении пробного заряда, будет равна сумме работ кулоновских полей тех зарядов, из которых состоит электростатическое поле. Соответственно, величина работы каждого заряда не будет зависеть от того, какой формы траектория. Значит, и полная работа не будет зависеть от пути – важно лишь местоположение начальной и конечной точки.

Поскольку у электростатического поля есть свойство потенциальности, мы можем добавить новое понятие – потенциальная энергия заряда в электрическом поле. Выберем какую-либо точку, поместим в нее разряд и примем его потенциальную энергию за 0 .

Потенциальная энергия заряда, помещенного в любую точку пространства относительно нулевой точки, будет равна той работе, которая совершается электростатическим полем при перемещении заряда из этой точки в нулевую.

Обозначив энергию как W , а работу, совершаемую зарядом, как A 10 , запишем следующую формулу:

Обратите внимание, что энергия обозначается именно буквой W , а не E , поскольку в электростатике E – это напряженность поля.

Потенциальная энергия электрического поля является определенной величиной, которая зависит от выбора точки отсчета (нулевой точки). На первый взгляд в таком определении есть заметная неоднозначность, однако на практике она, как правило, не вызывает недоразумений, поскольку сама по себе потенциальная энергия физического смысла не имеет. Важна лишь разность ее значений в начальной и конечной точке пространства.

Чтобы вычислить работу, которая совершается электростатическим полем при перемещении точечного заряда из точки 1 в точку 2 , нужно найти разность значений потенциальной энергии в них. Путь перемещения и выбор нулевой точки значения при этом не имеют.

A 12 = A 10 + A 02 = A 10 – A 20 = W p 1 – W p 2 .

Если мы поместим заряд q в электростатическое поле, то его потенциальная энергия будет прямо пропорциональна его величине.

Видео:Физика. 10 класс. Работа электрического поля по перемещению заряда /21.01.2021/Скачать

Понятие потенциала электрического поля

Потенциал электрического поля – это физическая величина, значение которой можно найти, разделив величину потенциальной энергии электрического заряда в электростатическом поле на величину этого заряда.

Он обозначается буквой φ . Это важная энергетическая характеристика электростатического поля.

Если мы умножим величину заряда на разность потенциалов начальной и конечной точки перемещения, то мы получим работу, совершаемую при этом перемещении.

A 12 = W p 1 – W p 2 = q φ 1 – q φ 2 = q ( φ 1 – φ 2 ) .

Потенциал электрического поля измеряется в вольтах ( В ) .

1 В = 1 Д ж 1 К л .

Разность потенциалов в формулах обычно обозначается Δ φ .

Чаще всего при решении задач на электростатику в качестве нулевой берется некая бесконечно удаленная точка. Учитывая это, мы можем переформулировать определение потенциала так:

Потенциал электростатического поля точечного заряда в некоторой точке пространства будет равен той работе, которая совершается электрическими силами тогда, когда единичный положительный заряд удаляется из этой точки в бесконечность.

Чтобы вычислить потенциал точечного заряда на расстоянии r , на котором размещается бесконечно удаленная точка, нужно использовать следующую формулу:

φ = φ ∞ = 1 q ∫ r ∞ E d r = Q 4 π ε 0 ∫ r ∞ d r r 2 = 1 4 π ε 0 Q r

С помощью нее мы также можем найти потенциал поля однородно заряженной сферы или шара при r ≥ R , что следует из теоремы Гаусса.

Видео:Работа электростатического поляСкачать

Изображение электрических полей с помощью эквипотенциальных поверхностей

Чтобы наглядно изобразить электростатические поля, кроме силовых линий используются поверхности, называемые эквипотенциальными.

Эквипотенциальная поверхность (поверхность равного потенциала) – это такая поверхность, у которой во всех точкам потенциал электрического поля одинаков.

Эквипотенциальные поверхности и силовые линии на изображении всегда находятся перпендикулярно друг другу.

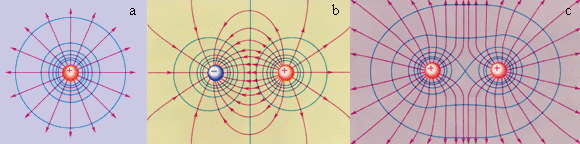
Если мы имеем дело с точечным зарядом в кулоновском поле, то эквипотенциальные поверхности в данном случае являются концентрическими сферами. На изображениях ниже показаны простые электростатические поля.

Рисунок 1 . 4 . 3 . Красным показаны силовые линии, а синим – эквипотенциальные поверхности простого электрического поля. На первом рисунке изображен точечный заряд, на втором –электрический диполь, на третьем – два равных положительных заряда.

Если поле однородное, то его эквипотенциальные поверхности являются параллельными плоскостями.

В случае малого перемещения пробного заряда q вдоль силовой линии из начальной точки 1 в конечную точку 2 мы можем записать такую формулу:

Δ A 12 = q E Δ l = q ( φ 1 – φ 2 ) = – q Δ φ ,

где Δ φ = φ 1 — φ 2 – изменение потенциала. Отсюда выводится, что:

E = — ∆ φ ∆ l , ( ∆ l → 0 ) или E = — d φ d l .

Это соотношение передает связь между потенциалом поля и его напряженностью. Буквой l обозначена координата, которую следует отсчитывать вдоль силовой линии.

Зная принцип суперпозиции напряженности полей, которые создаются электрическими разрядами, мы можем вывести принцип суперпозиции для потенциалов:

Видео:Силовые линии электрического поляСкачать

Работа по перемещению заряда в электростатическом поле с примерами

Содержание:

Работа по перемещению заряда в электростатическом поле:

В повседневной жизни мы довольно часто, особенно в сухую погоду, встречаемся с ситуацией, когда, коснувшись какого-либо тела, чувствуем неприятный удар. Как показывает опыт, таких сюрпризов можно ожидать от тел, имеющих высокий потенциал.

Видео:Электрическое поле/Напряженность и потенциал поля/Разность потенциалов/Работа поляСкачать

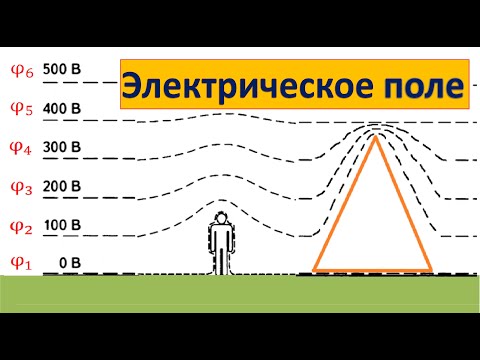
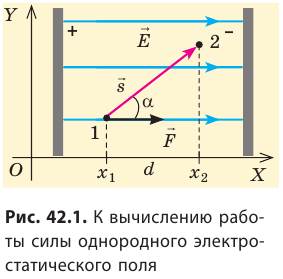
Работа по перемещению заряда в однородном электростатическом поле

Если электростатическое поле действует с некоторой силой на электрически заряженные тела, то оно способно совершить работу по перемещению этих тел.

Пусть в однородном электростатическом поле напряженностью

Вычислим работу А, которую совершает сила 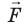, действующая на заряд со стороны электростатического поля. По определению работы: A=Fscosα.

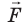
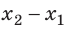
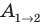
Поле однородное, поэтому сила постоянна, ее модуль равен: F=qE, а scosα=d=является проекцией вектора перемещения на направление силовых линий поля. Следовательно, работа сил однородного электростатического поля по перемещению электрического заряда q из точки 1 в точку 2 ( ) равна:

Обратите внимание! Если бы в данном случае заряд перемещался не из точки 1 в точку 2, а наоборот, то знак работы изменился бы на противоположный, то есть работа совершалась бы против сил поля.

Обратите внимание! Формула 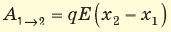будет справедлива в случаях движения заряда по любой траектории. То есть однородное электростатическое поле является потенциальным.

Потенциальным является любое электростатическое поле: работа электростатических (кулоновских) сил (как и работа гравитационных сил) не зависит от формы траектории, по которой перемещается заряд, а определяется начальным и конечным положениями заряда. Если траектория движения заряда замкнута, работа сил поля равна нулю.

Потенциальная энергия заряженного тела в поле, созданном точечным зарядом

Заряженное тело, помещенное в электростатическое поле, как и тело, находящееся в гравитационном поле Земли, обладает потенциальной энергией. Потенциальную энергию заряда, находящегося в электрическом поле, обычно обозначают символом . Согласно теореме о потенциальной энергии изменение потенциальной энергии заряда, взятое с противоположным знаком, равно работе, которую совершает электростатическое поле по перемещению заряда из точки 1 в точку 2 поля:

Потенциальную энергию взаимодействия двух точечных зарядов Q и q, расположенных на расстоянии r друг от друга, определяют по формуле:

Обратите внимание: 1) потенциальная энергия взаимодействия зарядов положительна ( > 0), если заряды одноименные, и отрицательна ( 0), то потенциал этого поля в любой точке является положительным ( ϕ > 0); 2) если поле создано отрицательным точечным зарядом (Q

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Урок 229. Работа электрического поля. Потенциал. Электрическое напряжениеСкачать

Работа на окружности в электростатическом поле

Раздел 8 ЭЛЕКТРИЧЕСТВО

8.6. Работа в электростатическом поле

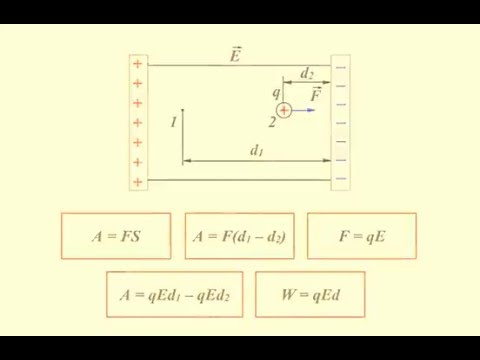
Рассмотрим однородное электрическое поле. Оно образуется между заряженными плоскостями, если они параллельны и бесконечно большие. Практически можно считать однородным электрическое поле между конечными параллельными заряженными плоскостями, если размеры их значительно больше, чем расстояние d между ними. Рассмотрим перемещение полем положительного заряда q в трех случаях. Пусть поле перемещает этот заряд из точки а в точку а ’ (рис. 8.3). Работа поля в этом случае

Если поле перемещает заряд из точки b в точку а ’, то работа

Подсчитаем теперь работу поля с перемещение электрического заряда из точки с в точку а ’ . Разобьем кривую s ₃ на большое количество участков, каждую из которых можно с большой точностью принять за прямую. Пусть таких участков будет n . Тогда

Поскольку поле однородное, сила 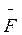остается постоянной для всех участков.

Из приведенных примеров можно сделать вывод, что работа электростатического поля не зависит от пути: она для трех случаев одинакова, хотя траектория перемещения электрического заряда разная.

Пусть электрическое поле образовано точечным зарядом q. Вычислим работу сил поля, совершаемой при перемещении вдоль силовой линии заряда q ₀ из точки 1, находящейся на расстоянии r ₁ от источника поля, в точку 2 на расстоянии r ₂ от него (рис. 8.4). Работа d А по перемещению заряда на бесконечно малом пути dr определится d А = Fdr . Поскольку F = q ₀ Е, то

Для поля точечного заряда назад

Тогда вся работа по перемещению заряда q ₀ из точки 1 в точку 2 будет

Величины обозначаются через φ ₁ и φ ₂ и нази льные потенциалами точек 1 и 2 соответственно. Следовательно,

Работа по перемещению заряда в электростатическом поле равна произведению заряда на разность потенциалов между начальной и конечной точками. Отсюда видно также, что эта работа не зависит от формы пути. Если откуда

Следовательно, потенциал — это физическая величина, численно равна работе, которую выполняет электрическое поле с перемещение единичного положительного заряда с определенной точки поля на бесконечность. Или потенциал определенной точки поля — это величина, численно равна работе, которую должна выполнить внешняя сила по перемещению единичного положительного заряда из бесконечности в эту точку. Потенциал данной точки поля определяет потенциальную энергию единичного положительного заряда, помещенного в эту точку. Если каждый из зарядов q ₁ , q ₂ . q_n образует в определенной точке поле с потенциалом соответствии φ ₁ , φ ₂ . φ _n , то потенциал поля, образованного в этой точке всеми зарядами, равна алгебраической сумме потенциалов полей, созданных каждым зарядом в отдельности:

На практике потенциал Земли условно взято равным нулю. Поэтому заземленный проводник имеет нулевой потенциал. В теоретических расчетах удобнее нулевой потенциал связать с точкой, находящейся на бесконечности.

Единицу разности потенциала можно ввести, воспользовавшись формулой

В СИ за единицу разности потенциалов взято вольт (1 В). Это разность потенциалов между такими двумя точками, перенос заряда в один кулон между которыми сопровождается выполнением работы в 1 Дж:

В системе СГСЭ за единицу разницы потенциалов взято разность потенциалов между такими двумя точками, перенос заряда в одну абсолютную электростатическую единицу заряда между которыми сопровождается выполнением работы в 1 эрг:

Часто пользуются внесистемной единицей работы и энергии, которое называется электрон-вольтом (эв). Один электрон-вольт равен работе, совершаемой при перемещении заряда, что равен заряду электрона, между двумя точками поля с разностью потенциалов в 1 В. Заряд электрона равен 1,6 ∙ 10 -19 Кл, тогда

Запишем значение работы однородного электрического поля по перемещению электрического заряда q на расстояние d от точки с потенциалом φ ₁ в точку с потенциалом φ ₂ . Тогда

Геометрическое место точек с одинаковым потенциалом называют эквипотенциальной поверхностью. Понятно, что работа, которую выполняет поле по перемещению электрического заряда по той самой еквіпотенціальній поверхности, равна нулю. Поскольку сила, действующая со стороны поля на заряд, не равна нулю, то работа по перемещению заряда может равняться нулю только тогда, когда направление действия силы перпендикулярен к направлению перемещения. Учитывая, что направление действия силы на заряд совпадает с направлением вектора напряженности поля, можно сделать вывод о перпендикулярность линии напряженности к еквіпотенціальних поверхностей.

Электростатическое поле можно изобразить графически с помощью силовых линий, но и с помощью еквіпотенціальних поверхностей. Вокруг каждой системы зарядов проводят бесконечное множество еквіпотенціальних поверхонь. их принято проводить так, чтобы разности потенциалов между любыми соседними эквипотенциальными поверхностями были одинаковые.

Зная размещения силовых линий электростатического поля, можно построить эквипотенциальные поверхности и, наоборот, по известным размещением еквіпотенціальних поверхностей можно в каждой точке поля определить размещение силовых линий.

Поскольку работа электростатического поля по перемещению заряда не зависит от формы пути, а определяется только потенциалами конечных точек, то получается, что работа по замкнутому контуру (рис. 8.5) в электростатическом поле (АаВ d А, А b В d А, АсВ d А) равна нулю.