| Эта работа успешно выполнена Преподавателю: в основное пространство, в подстраницу Данное задание было проверено и зачтено. Проверено Frolov и VadimVV. |
| Нахождение собственных чисел квадратной матрицы методом QR разложения | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(n^3)+N*O(n^2)[/math] |
| Объём входных данных | [math] n^2 [/math] |
| Объём выходных данных | [math] n [/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(n^2)+N*O(n)[/math] |
| Ширина ярусно-параллельной формы | [math]O(n^2)[/math] |
Основные авторы описания:
- Смирнова А.С. — описание теоретической части
- Киямова А. — описание программистской части
Содержательно все пункты обсуждались авторами вместе, и их вклад был равным.
Задача нахождения собственных значений и собственных векторов для матрицы [math]A[/math] заключается в поиске таких чисел [math]lambda[/math] , которые удовлетворяют уравнению:
[math]Ax=lambda x[/math] , при этом, числа [math]lambda[/math] называются собственными значениями, а вектора [math]x[/math] — собственными векторами [1] .
Данная задача является одной из важнейших задач линейной алгебры. Собственные вектора и собственные значения применяются в различных областях науки: в аналитической геометрии, при решении систем интегральных уравнений, в математической физике. Однако не существует простых алгоритмов прямого вычисления собственных значений для матриц в общем случае, поэтому данная задача на практике решается численными методами. Одним из таких методов является QR-алгоритм.
- Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.2.1 QR-разложение матрицы
- 1.2.2 QR-алгоритм нахождения собственных чисел
- 1.2.3 Сходимость алгоритма
- 1.2.4 Вещественный вариант QR-алгоритма
- 1.2.5 Приведение матрицы к форме Хессенберга
- 1.2.6 QR-алгоритм со сдвигами
- 1.3 Вычислительное ядро алгоритма
- 1.3.1 Базовый алгоритм
- 1.3.2 Модифицированный алгоритм
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.5.1 Базовый алгоритм
- 1.5.2 Модифицированный алгоритм
- 1.6 Последовательная сложность алгоритма
- 1.6.1 Базовый алгоритм
- 1.6.2 Модифицированный алгоритм
- 1.7 Информационный граф
- 1.7.1 Базовый алгоритм
- 1.7.2 Модифицированный алгоритм
- 1.8 Ресурс параллелизма алгоритма
- 1.8.1 Базовый алгоритм
- 1.8.2 Модифицированный алгоритм
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- VMath
- Инструменты сайта
- Основное
- Навигация
- Информация
- Действия
- QR-алгоритм поиска всех собственных чисел матрицы
- Источники
- Реализация метода главных компонент на C#
- Метод главных компонент (пока без кода)
- QR декомпозиция
- Итеративный QR метод
- Реализация метода главных компонент
- Тестирование
- 🎬 Видео
Видео:Собственные векторы и собственные числа линейного оператораСкачать

Содержание
Видео:Собственные значения и собственные векторы матрицы (4)Скачать

1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
QR-алгоритм — это численный метод в линейной алгебре, предназначенный для решения полной проблемы собственных значений, то есть отыскания всех собственных чисел матрицы. При этом алгоритм позволяет найти и собственные вектора матрицы. Он был разработан в конце 1950-х годов независимо В. Н. Кублановской(Россия) и Дж. Фрэнсисом(Англия). Открытию QR-алгоритма предшествовал LR-алгоритм, который использовал LU-разложение вместо QR-разложения. В настоящее время LR-алгоритм используется очень редко ввиду своей меньшей эффективности, однако он был важным шагом на пути к открытию QR-алгоритма [2] .
Суть базового QR-алгоритма заключается в итерационном приведении матрицы [math]A[/math] к некоторой подобной ей матрице [math]A_N[/math] при помощи QR-разложения. Матрица [math]A_N[/math] является правой верхней треугольной матрицей, а значит ее диагональ содержит собственные значения. В силу подобия матриц [math]A[/math] и [math]A_N[/math] их наборы собственных значений совпадают. Таким образом задача поиска собственных значений матрицы [math]A[/math] сводится к задаче выведения матрицы [math]A_N[/math] и поиска собственных значений для нее, что является тривиальной задачей.
Однако базовый QR-алгоритм может обладать очень низкой скоростью сходимости, поэтому существует несколько способов ускорить его:
- Перед итерациями привести матрицу [math]A[/math] к подобной ей матрице [math]A_H[/math] , которая будет иметь форму Хессенберга. Данный шаг позволит ускорить процесс QR-разложения.
- Использовать QR-алгоритм со сдвигами. Это позволит уменьшить количество итераций алгоритма.
В дальнейшем, в данной статье под модифицированным алгоритмом будет пониматься алгоритм, использующий сдвиги и матрицу с формой Хессенберга. Под базовым алгоритмом будет пониматься алгоритм, не использующий данные приемы.
1.2 Математическое описание алгоритма
1.2.1 QR-разложение матрицы
Основой алгоритма является тот факт, что любую вещественную матрицу можно разложить на произведение двух матриц следующего вида:
[math]A=QR[/math] , где [math]Q[/math] — ортогональная матрица ( [math]Q^T=Q^[/math] ), [math]R[/math] — верхняя треугольная матрица.
Данное разложение называется QR-разложением.
Есть несколько алгоритмов вычисления QR-разложения матрицы [3] [4] . Кратко опишем их в данной статье.
1.2.1.1 Метод Хаусхолдера (отражений) QR-разложения квадратной матрицы
Суть метода Хаусхолдера заключается в последовательном приведении матрицы [math]A[/math] к верхней треугольной форме при помощи домножения ее на так называемые матрицы отражения. Получившаяся треугольная матрица будет искомой матрицей [math]R[/math] , а матрица [math]Q[/math] будет равна произведению сопряженных матриц отражения.
На [math]i[/math] -ом шаге задача [math]i[/math] -ой матрицы отражения заключается в обнулении всех поддиагональных элементов [math]i[/math] -го столбца матрицы [math]A[/math] (при этом столбцы левее [math]i[/math] -го не изменяются). Таким образом, алгоритм состоит из [math]n-1[/math] шагов, на каждом из которых вычисляется очередная матрица отражения, после чего найденное отражение применяется к матрице, которая является результатом предыдущего шага.
Матрица отражения имеет вид [math]E-fracvv^*[/math] , где вектор [math]v[/math] вычисляется из текущего [math]i[/math] -го столбца матрицы при помощи использования операции скалярного произведения векторов. Данное представление матриц отражения позволяет хранить их в виде одного вектора и сводит домножение матрицы отражения на текущую матрицу к арифметическим операциям над векторами (скалярное произведение и сложение векторов).
1.2.1.2 Метод Гивенса (вращений) QR-разложения квадратной матрицы
Суть метода Гивенса заключается в последовательном приведении матрицы [math]A[/math] к верхней треугольной форме при помощи домножения ее на так называемые матрицы вращения. Получившаяся треугольная матрица будет искомой матрицей [math]R[/math] , а матрица [math]Q[/math] будет равна произведению сопряженных матриц вращения.
На каждом шаге задачей матрицы вращения является обнуление одного поддиагонального элемента. Вначале обнуляются все поддиагональные элементы 1-го столбца, затем 2-го и так далее до [math](n-1)[/math] -го. Таким образом, алгоритм состоит из [math]frac[/math] шагов на каждом из которых вычисляется очередная матрица вращения, после чего она применяется к матрице, которая является результатом предыдущего шага.
Матрицы вращения [math]T_[/math] по ствоей структуре очень близки к единичным матрицам, за исключением четырех элементов: элементы с номерами [math]ii[/math] и [math]jj[/math] содержат некоторое число-параметр [math]c[/math] , элементы с номерами [math]ij[/math] и [math]ji[/math] содержат числа-параметры [math]-s[/math] и [math]s[/math] соответственно. Вычисление параметров [math]c[/math] и [math]s[/math] происходит на каждом шаге в зависимости от текущей матрицы и состоит из простых численных арифметических операций. Умножение матрицы вращения на текущую матрицу может быть представлено как последовательное изменение элементов с номерами [math]ik[/math] и [math]kk[/math] для всех столбцов [math]k[/math] находящихся правее столбца [math]i[/math] . Каждое такое изменение по своей структуре эквивалентно операции перемножения двух комплексных чисел.
1.2.2 QR-алгоритм нахождения собственных чисел
Пусть матрица [math]A[/math] — матрица, для которой мы хотим найти собственные значения. Тогда итерационный процесс строится следующим образом:
- [math]A_0=A[/math] .
- Пусть имеется матрица [math]A_k[/math] , тогда матрица [math]A_[/math] строится следующим образом:
- Строится QR-разложение: [math]A_k=Q_kR_k[/math] .
- Вычисляется [math]A_=R_kQ_k[/math] .
Таким образом матрицы [math]A_[/math] и [math]A_[/math] подобны для [math]forall k[/math] , а значит, в силу транзитивности подобия, все матрицы [math]A_[/math] подобны матрице [math]A[/math] и имеют одинаковый набор собственных значений.
1.2.3 Сходимость алгоритма
Предположим, что для [math]forall m[/math] выполнены следующие условия:
1. [math]A=XLambda X^[/math] , где [math]Lambda =begin Lambda_1 & 0\ 0 & Lambda_2 end, Lambda_1inmathbb^,Lambda_2inmathbb^ [/math] .
2. [math]left | lambda_1 right | geq . geq left | lambda_m right | gt left | lambda_ right | geq . geq left | lambda_ right | gt 0 [/math] , где [math] = lambda(Lambda_1), <lambda_. lambda_> = lambda(Lambda_2) [/math] .
3. Ведущая подматрица порядка [math]m[/math] в [math]X^[/math] невырождена.
Тогда при [math] k rightarrow infty [/math] последовательность матриц [math]A_k[/math] сходится к матрице с верхней треугольной формой [5] .
Таким образом, на практике необходимо выполнять итерации до тех пор пока матрица [math]A_k[/math] не станет треугольной (также можно продолжать выполнять их пока искомая матрица не будет найдена с некоторой заранее заданной точностью [math]varepsilon[/math] ). Если итерации закончились на шаге [math]N[/math] , то числа на диагонали матрицы [math]A_N[/math] будут считаться собственными значениями матрицы [math]A[/math] .
1.2.4 Вещественный вариант QR-алгоритма
Если вещественная матрица [math]A[/math] имеет различные вещественные собственные значения, то, как было описано ранее, QR-алгоритм сходится к матрице с верхней треугольной формой, на диагонали которой находятся собственные значения. Однако вещественная матрица может иметь комплексные собственные значения. В данном случае алгоритм будет сходиться не к верхней треугольной матрице, а к блочной верхней треугольной матрице, которая на диагонали содержит блоки 1-го и 2-го порядка. Блоки 1-го порядка содержат различные вещественные собственные значения, блоки 2-го порядка соответствуют парам комплексных сопряженных собственных значений [6] .
[math]A_N= begin blacksquare& bullet& bullet& cdots& cdots& cdots& cdots& cdots& bullet\ 0& blacksquare& blacksquare& bullet& ddots& ddots& ddots& ddots& vdots\ 0& blacksquare& blacksquare& bullet& bullet& ddots& ddots& ddots& vdots\ vdots& 0& 0& blacksquare& bullet& bullet& ddots& ddots& vdots\ vdots& ddots& 0& 0& blacksquare& bullet& bullet& ddots& vdots\ vdots& ddots& ddots& 0& 0& blacksquare& blacksquare& ddots& vdots\ vdots& ddots& ddots& ddots& 0& blacksquare& blacksquare& ddots& bullet\ vdots& ddots& ddots& ddots& ddots& ddots& ddots& ddots& bullet\ 0& cdots& cdots& cdots& cdots& cdots& 0& 0& blacksquare end[/math] .
В дальнейшем, в данной статье, матрицы, имеющие вышеописанную форму, будут называться квазитреугольными.
1.2.5 Приведение матрицы к форме Хессенберга
Матрицей, имеющей форму Хессенберга, называется такая матрица, у которой все элементы, находящиеся ниже первой поддиагонали, равны нулю ( [math]a_=0[/math] при [math]ilt j+1[/math] ). Пример такой матрицы приведен ниже:
[math]begin 1& 2& 3& 4\ 2& 5& 6& 7\ 0& 3& 8& 9\ 0& 0& 4& 1 end[/math]
Любую матрицу [math]A[/math] можно привести к подобной ей матрице [math]A_H[/math] , имеющей форму Хессенберга (в силу подобия данные матрицы будут иметь одинаковые собственные значения). Наличие нулевых элементов в данной матрице позволяет ускорить процесс QR-разложения, причем данное ускорение будет иметь место на каждой итерации алгоритма, т.к. матрица с формой Хессенберга инвариантна относительно QR-итерации. Ускорение можно получить за счет использования модифицированного метода Гивенса(вращений) QR-разложения, который из-за изначального наличия нулевых элементов будет состоять не из [math]frac[/math] шагов, а из [math]n-1[/math] шагов (будет происходить домножение только на те матрицы вращения [math]T_[/math] , у которых [math]i=j+1[/math] ).
Одним из способов приведения матрицы к форме Хессенберга является Метод Хаусхолдера (отражений) [7] . Суть метода Хаусхолдера заключается в последовательном приведении матрицы [math]A[/math] к форме Хессенберга при помощи домножения ее на так называемые матрицы отражения.
На [math]i[/math] -ом шаге задача [math]i[/math] -ой матрицы отражения заключается в обнулении поддиагональных элементов [math]i[/math] -го столбца матрицы [math]A[/math] (при этом столбцы левее [math]i[/math] -го не изменяются). Таким образом, алгоритм состоит из [math]n-2[/math] шагов, на каждом из которых вычисляется очередная матрица отражения, после чего найденное отражение применяется к матрице, которая является результатом предыдущего шага.
Матрица отражения имеет вид [math]E-fracww^*[/math] , где вектор [math]w[/math] вычисляется из текущего [math]i[/math] -го столбца матрицы при помощи использования операции скалярного произведения векторов. Данное представление матриц отражения позволяет хранить их в виде одного вектора и сводит домножение матрицы отражения на текущую матрицу к арифметическим операциям над векторами (скалярное произведение и сложение векторов).
В основной статье «Метод Хаусхолдера (отражений) приведения матрицы к хессенберговой (почти треугольной) форме» данный алгоритм описан более подробно с той лишь разницей, что для QR-алгоритма нет необходимости обнулять наддиагональные элементы, как это сделано в вышеупомянутой статье.
1.2.6 QR-алгоритм со сдвигами
QR-алгоритм со сдвигами позволяет сократить количество итераций, необходимых для сходимости [8] . Пусть у нас есть матрица [math]A_k[/math] , тогда процесс перехода к матрице [math]A_[/math] выглядит следующим образом:
- На каждом шаге подбирается число [math]nu_k[/math] и ищется следующее QR-разложение: [math]A_k-nu_kE=Q_kR_k[/math] .
- Вычисляется матрица [math]A_[/math] : [math]A_ = R_kQ_k+nu_kE[/math] .
При этом сохраняется свойство подобия матриц [math]A_k[/math] и [math]A_[/math] :
В качестве параметра [math]nu_k[/math] может быть взят последний диагональный элемент матрицы [math]A_k[/math] .
1.3 Вычислительное ядро алгоритма
1.3.1 Базовый алгоритм
QR-алгоритм обладает двумя вычислительными ядрами, которые повторяются на каждой итерации:
- Вычисление QR-разложения матрицы: [math]A_k=Q_kR_k[/math] . Существует несколько методов решения данной задачи:
- Метод Хаусхолдера (отражений): вычислительное ядро данного алгоритма состоит из операций скалярного произведения, необходимых для вычисления матрицы отражения, и из операций скалярного произведения, необходимых для пересчета матрицы на каждом шаге.
- Метод Гивенса (вращений): вычислительное ядро данного алгоритма состоит из численных арифметических операций, необходимых для вычисления параметров матрицы вращения, и из операций (эквивалентных перемножению комплексных чисел), необходимых для пересчета матрицы на каждом шаге.
- Перемножение двух плотных матриц: [math]A_=R_kQ_k[/math] .
1.3.2 Модифицированный алгоритм
Модифицированный QR-алгоритм обладает тремя вычислительными ядрами, первое вычисляется единожды, второе и третье повторяются на каждой итерации:
- Приведение изначальной матрицы к форме Хессенберга: вычислительное ядро данного алгоритма состоит из операций скалярного произведения, необходимых для вычисления матрицы отражения, и из операций скалярного произведения, необходимых для пересчета матрицы на каждом шаге.
- Вычисление QR-разложения матрицы: [math]A_k-nu_kE=Q_kR_k[/math] при помощи модифицированного метода Гивенса (вращений). Описание вычислительного ядра не отличается от приведенного в описании базового алгоритма, единственная разница заключается в значительно меньшем количестве матриц вращения.
- Перемножение двух плотных матриц: [math]A_-nu_kE=R_kQ_k[/math] .
1.4 Макроструктура алгоритма
Как уже было описано ранее, базовый QR-алгоритм содержит в себе две макрооперации:
- Вычисление QR-разложения матрицы: [math]A_k=Q_kR_k[/math] .
- Перемножение двух плотных матриц: [math]A_=R_kQ_k[/math] .
В случае модифицированного QR-алгоритма появляется еще макрооперация приведения матрицы к форме Хессенберга.
1.5 Схема реализации последовательного алгоритма
1.5.1 Базовый алгоритм
Опишем необходимый для реализации цикл при помощи псевдокода:
1.5.2 Модифицированный алгоритм
Опишем необходимый для реализации цикл при помощи псевдокода:
1.6 Последовательная сложность алгоритма
1.6.1 Базовый алгоритм
Подсчитаем сложность одной итерации QR-алгоритма (расчет сложностей для QR-разложения и перемножения матриц представлен в статьях, посвященных данным алгоритмам).
- QR-разложение матрицы.
- Метод Хаусхолдера (отражений) имеет сложность [math]fracn^3[/math] .
- Метод Гивенса (вращений) имеет сложность [math]2n^3[/math] .
- Перемножение двух плотных матриц имеет сложность [math]n^3[/math] .
- Проверка матрицы на квазитреугольную форму состоит из набора сравнений элементов с номерами [math]ij[/math] ( [math]igt j+1[/math] ) с нулем (таких элементов [math]frac[/math] ). Поддиагональные элементы с номерами [math]ij[/math] ( [math]i=j+1[/math] ) должны быть проверены на соответствие необходимой квазитреугольной форме. Для этого достаточно для каждого такого элемента проверить следующее условие: [math]a_==0 vee a_==0 wedge a_==0[/math] (либо поддиагональный элемент равен 0, либо, в противном случае, соседние поддиагональные элементы равны 0, чтобы текущий элемент соответствовал блоку 2-го порядка). Таких проверок поддиагональных элементов будет [math]n-1[/math] . После данных проверок следует набор логических операций «И» между результатами всех сравнений (таких операций будет [math]frac-1[/math] ).
- Сравнение новой матрицы с предыдущей состоит из операций вычитания и сравнения для каждой пары ненулевых соответствующих элементов (такие пары имеют номера элементов [math]ij[/math] ( [math]i geq j+1[/math] ), количество таких пар равно [math]frac+(n-1)[/math] ), а также из набора логических операций «И» между результатами сравнений (таких операций будет [math]frac+(n-1)-1[/math] ).
Итого, в сумме получаем [math]O(n^3)[/math] — сложность алгоритма на каждой итерации. Если алгоритм остановился на итерации с номером [math]N[/math] , то общая сложность алгоритма будет равна [math]N*O(n^3)[/math] .
1.6.2 Модифицированный алгоритм
Отличия от базового алгоритма заключаются в следующем:
- Метод Хаусхолдера (отражений) имеет последовательную сложность [math]O(n^3)[/math] .
- QR-разложение матрицы, имеющей форму Хессенберга будет иметь сложность порядка [math]O(n^2)[/math] [8] .
Стоит заметить, что вычисление сдвигов по сравнению с другими операциями не обладает высокой сложностью, однако позволяет значительно сократить количество необходимых итераций.
Итого, в сумме получаем [math]O(n^2)[/math] — сложность алгоритма на каждой итерации. Сложность всего алгоритма, с учетом приведения матрицы к форме Хессенберга, будет равна [math]O(n^3)+N*O(n^2)[/math]
1.7 Информационный граф
1.7.1 Базовый алгоритм
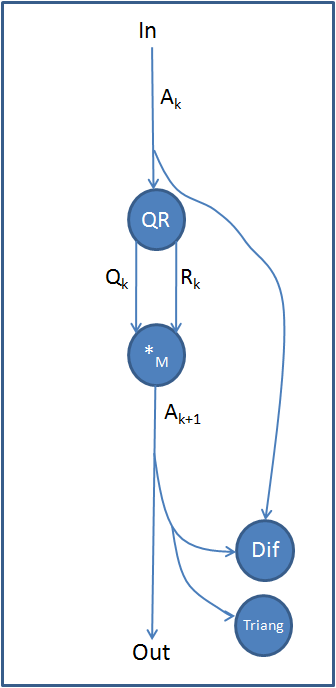
На рисунках 1 и 2 изображен информационный граф QR-алгоритма. Вершины данного графа обозначают следующее:
- QR — операция QR-разложения матрицы.
- *M — операция перемножения матриц.
- Triang — операция проверки матрицы на квазитреугольную форму.
- Dif — операция проверки различия элементов двух матриц не более чем на некоторое заданное число.
- Iteri — итерация алгоритма
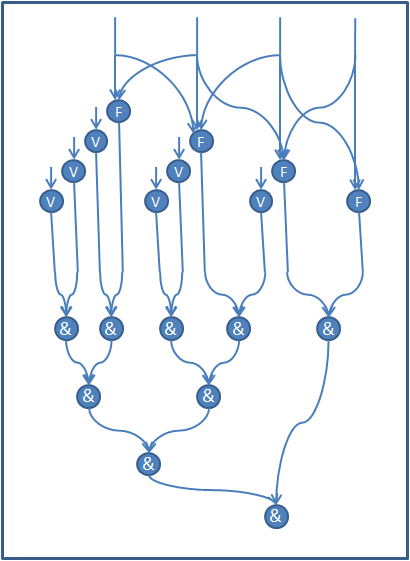
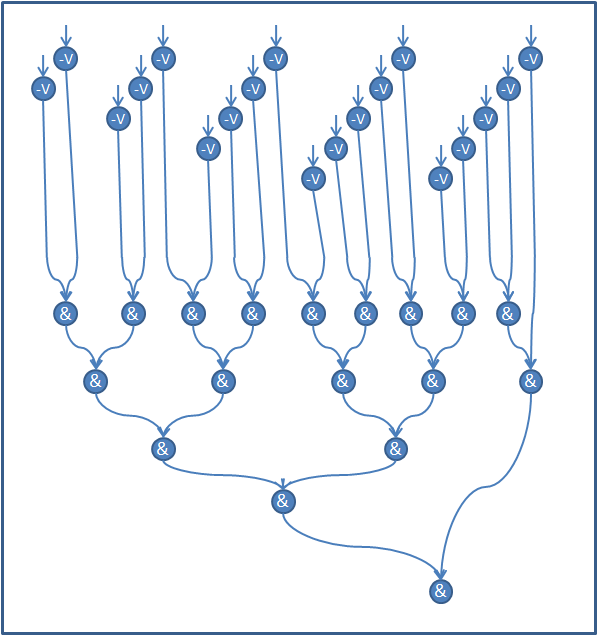
Подробные графы операций QR-разложения (Метод Хаусхолдера (отражений), Метод Гивенса (вращений)) и перемножения матриц можно найти в статьях, посвященных этим алгоритмам. Далее рассмотрим информационные графы операций Triang (рис.3) и Dif (рис.4) на примере матрицы размера [math]5 times 5[/math] . Графы для других матриц выглядят аналогичным образом.
Вершины V соответствуют операции сравнения с 0. Вершины F соответствуют проверке поддиагональных элементов на соответствие квазитреугольной форме, которая была описана в предыдущем разделе. Вершины & соответствуют логической операции «И».
Вершины -V соответствуют операции вычитания и сравнения с 0. Вершины & соответствуют логической операции «И».
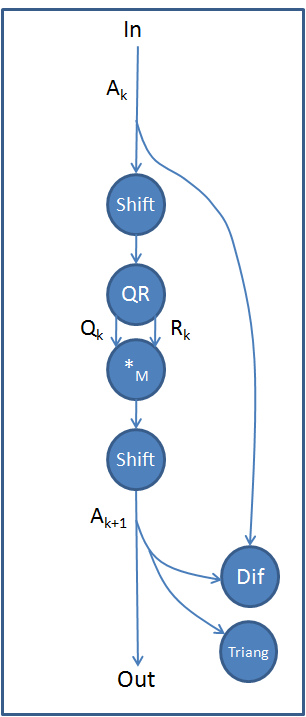
1.7.2 Модифицированный алгоритм
На рисунках 5 и 6 изображен информационный граф модифицированного QR-алгоритма. Дополнительные вершины для этого графа обозначают следующее:
- Shift — операция сдвига
- H — операция приведения матрицы к форме Хессенберга
1.8 Ресурс параллелизма алгоритма
1.8.1 Базовый алгоритм
На макроуровне (который можно увидеть на информационном графе QR-алгоритма) алгоритм не обладает ресурсами параллелизма. Все макрооперации внутри итерации, а также сами итерации выполняются последовательно (за исключением операций Triag и Dif, которые могут выполняться параллельно). Основной ресурс параллелизма заложен отдельно в каждой из макроопераций. На каждой итерации алгоритм имеет следующие параллельные характеристики:
- QR-разложение матрицы (описание ресурсов параллелизма для алгоритмов QR-разложения можно найти в статьях, посвященных этим алгоритмам).
- Метод Хаусхолдера (отражений) имеет высоту ярусно-параллельной формы [math]O(n^2)[/math] и ширину ярусно-параллельной формы [math]O(n)[/math] .
- Метод Гивенса (вращений) имеет высоту ярусно-параллельной формы [math]11n-16[/math] и ширину ярусно-параллельной формы [math]O(n^2)[/math] .
- Перемножение двух плотных матриц имеет высоту ярусно-параллельной формы [math]n[/math] и ширину ярусно-параллельной формы [math]n^2[/math] .
- Проверка матрицы на выходе из итерации.
- Проверка матрицы на квазитреугольную форму состоит из одного яруса сравнений для каждого элемента и последующих ярусов, вычисляющих итоговый результат при помощи логической операции «И». Для вычисления итогового результата можно использовать метод сдваивания, который дает высоту ярусно-параллельной формы порядка логарифма от количества элементов, над которыми совершается операция. Таким образов высота ярусно-параллельной формы будет равна [math]O(log_2n)[/math] . Ширина ярусно-параллельной формы достигается на ярусе сравнений для каждого элемента и равна [math]O(n^2)[/math] .
- Сравнение новой матрицы с предыдущей состоит из одного яруса сравнений для каждого элемента и последующих ярусов, вычисляющих итоговый результат при помощи логической операции «И». Высота ярусно-параллельной формы будет равна [math]O(log_2n)[/math] . Ширина ярусно-параллельной формы достигается на ярусе сравнений для каждого элемента и равна [math]O(n^2)[/math] .
Таким образом, основной вклад в высоту ярусно-параллельной формы одной итерации вносит операция QR-разложения матрицы и она будет равна [math]O(n)[/math] , если использовать метод Гивенса. Ширина ярусно-параллельной формы будет равна [math]O(n^2)[/math] . Если алгоритм остановился на итерации с номером [math]N[/math] , то параллельные характеристики для всего алгоритма будут равны [math]N*O(n)[/math] для высоты и [math]O(n^2)[/math] для ширины ярусно-параллельной формы.
1.8.2 Модифицированный алгоритм
Отличия от базового алгоритма заключаются в следующем:
- Приведение матрицы к форме Хессенберга имеет высоту ярусно-параллельной формы [math]O(n^2)[/math] и ширину ярусно-параллельной формы [math]O(n^2)[/math] .
- QR-разложение матрицы модифицированным методом Гивенса (вращений) имеет высоту ярусно-параллельной формы [math]O(n)[/math] и ширину ярусно-параллельной формы [math]O(n)[/math] .
- Операция сдвига (вычитание из диагональных элементов матрицы одного числа) имеет высоту ярусно-параллельной формы [math]O(1)[/math] и ширину ярусно-параллельной формы [math]O(n)[/math] .
Таким образом, итоговые характеристики всего модифицированного алгоритма будут следующие: высота ярусно-параллельной формы [math]O(n^2)+N*O(n)[/math] и ширина ярусно-параллельной формы [math]O(n^2)[/math] .
1.9 Входные и выходные данные алгоритма
квадратная вещественная плотная матрица [math]A[/math] : [math]A in R^[/math] .
Объем входных данных:
[math]n^2[/math] (необходимо хранить все элементы матрицы).
собственные значения матрицы [math]A[/math] .
Объем выходных данных:
[math]n[/math] (квадратная матрица размера [math]n times n[/math] имеет ровно [math]n[/math] собственных значений при этом некоторые из них могут быть комплексными).
1.10 Свойства алгоритма
- Cоотношение последовательной и параллельной сложности алгоритма квадратично, что дает довольно большой выигрыш.
- Вычислительная мощность, которая показывает, сколько операций приходится на единицу переданных данных, равна [math]frac=N*O(n)[/math] , а значит перемещение данных для их обработки не будет составлять большой проблемы.
- Алгоритм является недетерминированным, т.к. заранее неизвестно сколько итераций необходимо совершить до момента сходимости.
- Скорость сходимости алгоритма зависит от собственных значений. Чем ближе по модулю соседние собственные значения, тем меньше скорость сходимости. Этот недостаток призван решить QR-алгоритм со сдвигами.
Видео:Собственные векторы и собственные значения матрицыСкачать

2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
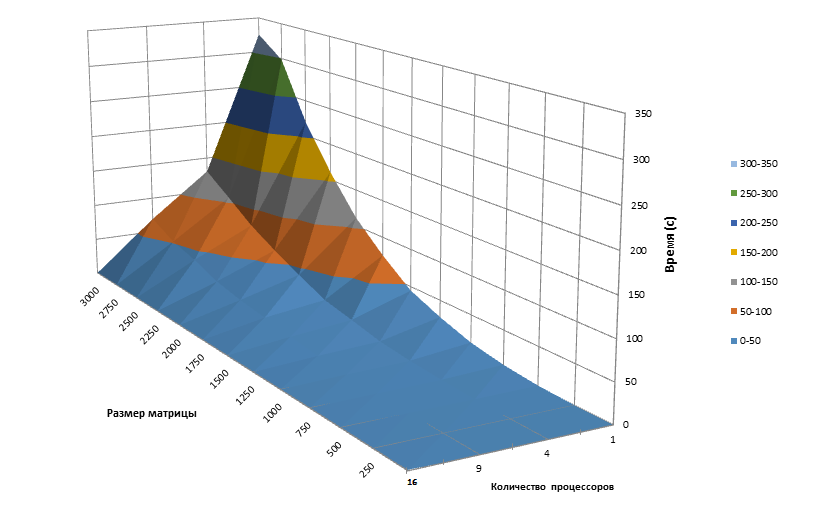
Масштабируемость алгоритма (рис.7) исследовалась на основе реализации алгоритма в библиотеке ScaLAPACK v2.0.0: функция pdhseqr. Время работы было замерено для различных размеров матрицы, а также различного числа процессоров.
При увеличении числа процессоров время работы программы увеличивается при малом размере матрицы, распараллеливание алгоритма неэффективно. Однако при больших размерах матрицы (более [math] 10^3times10^3[/math] ) время работы параллельной реализации значительно меньше последовательной.
Все вычисления были проведены на суперкомпьютере Regatta. Библиотека ScaLAPACK v2.0.0 была установлена вручную. Компиляция проводилась с использованием компилятора mpicxx с опциями -lscalapack и -llapack с указанием полного пути до используемых библиотек.
Видео:QR-разложениеСкачать
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Видео:Собственные значения и собственные векторыСкачать

QR-алгоритм поиска всех собственных чисел матрицы
Этот алгоритм основан на QR-разложении матрицы $ A $.
Теорема. Спектр матрицы $ A $ совпадает со спектром матрицы $ P^ A P $ при произвольной ортогональной матрице $ P $.
Доказательство. $$ det (P^ A P-lambda E)=det (P^ A P- lambda P^ E P)=det P^ (A -lambda E ) P = det (A -lambda E ) P P^ = det (A -lambda E ) , . $$ ♦
Пусть QR-разложение матрицы $ A $ имеет вид $$ A=Q_1R_1 , , $$ где $ Q_1 $ — ортогональная, а $ R_1 $ — верхнетреугольная матрицы. Тогда матрица $$ A_2=R_1Q_1 $$ имеет тот же спектр, что и матрица $ A $. Действительно, поскольку $$ A_2=Q_1^ A Q_1 , $$ то сработает предыдущая теорема. Вычислим QR-разложение матрицы $ A_2 $ $$ A_2=Q_2R_2 $$ и переставим местами матрицы этого произведения: $$ A_3=R_2Q_2 , . $$ Матрица $$ A_3= Q_2^ A_2 Q_2=Q_2^ Q_1^ A Q_1 Q_2 $$ продолжает иметь те же собственные числа, что и матрица $ A $. Утверждается, что бесконечная последовательность матриц $$ <A_j=R_Q_>_^ $$ как правило, сходится к матрице $ A_ $, которая будет верхнетреугольной.
Теорема [1]. Если все собственные числа матрицы $ A $ различны по модулю, то матрица $ A_ $ является верхнетреугольной и на ее главной диагонали стоят собственные числа матрицы $ A $.
Пример. Найти все собственные числа матрицы
$$ A=left(begin 2 & 3 &-1\ 7 & 3 & 3 \ -1 & -2 & 4 end right) , . $$
Решение. $$ A_1=Aapprox underbrace<left(begin 0.272165 & 0.759752 & 0.590511 \ 0.952579 & -0.299517 & -0.053683 \ -0.136083& -0.577119 & 0.805242 end right)>_ underbrace<left(begin 7.348469 & 3.946400 & 2.041241\ 0 & 2.534941 & -3.966781 \ 0 & 0 & 2.469409 end right)>_ $$ Теперь переставляем матрицы произведения местами и строим QR-разложение получившейся матрицы: $$ quad Rightarrow quad A_2 = R_1Q_1approx left(begin 5.481481 & 3.222957 & 5.771191 \ 2.954542 & 1.530046 & -3.3303021 \ -0.336044 & -1.425143 & 1.988472 end right)approx $$ $$ approxunderbrace<left(begin -0.878992 & 0.022595 & 0.476300\ 0.473781 & -0.154267 & -0.867026 \ 0.053886 & -0.987771 & 0.146304 end right)>_
underbrace<left(begin -6.236096& -3.634658 & -3.387848\ 0 & 1.244502 & -1.319999\ 0 & 0 & 5.927198 end right)>_ $$ Продолжим процесс: $$ quad Rightarrow quad A_3 = R_2Q_2approx left(begin 7.020952& 3.766220 & -0.314568\ -0.660752 & 1.111870 & -1.272137\ 0.319398 & -5.854713 & 0.867177 end right) approx $$ $$ approx underbrace<left(begin -0.994581 & -0.065879 & 0.080426 \ 0.093601 & -0.230749 & 0.968501 \ -0.045246 & 0.970780 & 0.235665 end right)>_
underbrace<left(begin -7.059205 & -3.376839 & 0.154554 \ 0 & -6.188319 & 1.156106 \ 0 & 0 & -1.053002 end right)>_ $$ Замечаем тенденцию убывания элементов матриц $ $, стоящих под главной диагональю. $$ Rightarrow dots Rightarrow A_ approx left(begin mathbf_ & 2.758769 & -2.160057\ -0.0467437 & mathbf_ & -5.341014\ 0.000018 &-0.005924 & mathbf_ end right) approx $$ $$ underbrace<left(begin -0.999972 & -0.007483 & 0.000007 \ 0.007483 & -0.999971 & 0.001339 \ -0.000003 & 0.001339 & 0.999999 end right)>_<Q_> underbrace<left(begin -6.246197 & -2.725694 & 2.120031\ 0 & -4.429817 & 5.354807 \ 0 & 0 & -1.662479 end right)>_<R_> , . $$ Матрица $ Q_j $ уже близка к диагональной (с элементами $ pm 1 $), верхнетреугольность матрицы $ A_j $ также заметна, но точность приближения еще не достаточна. $$ Rightarrow dots Rightarrow A_ approx left(begin mathbf_ & 2.805821 & -2.020513 \ -0.001776 & mathbf_ & -5.388407\ 0 & 0 & -mathbf end right) approx $$ Точность приближения минимильного собственного числа существенно выше точностей приближения остальных чисел. $$ Rightarrow dots Rightarrow A_ approx left(begin mathbf_ & 2.807524 & -2.015076\ -0.000073 & mathbf_ & -5.390442\ 0 & 0 & -mathbf end right) , . $$ ♦
К сожалению условие теоремы достаточно ограничительно: собственные числа вещественной матрицы $ A $ могут оказаться и мнимыми, но тогда они одинаковы по модулю. Посмотрим как это обстоятельство скажется на структуре матрицы $ A_ $.
Пример. Вычислить $ A_ $ для матрицы
$$ A= left(begin 2 & 7 & 18 & 28 \ 1 & 8 & 2 & 8 \ 3 & 1 & 4 & 1 \ 5 & 9 & 26 & 5 end right) , . $$
Решение. Здесь вычисленная по алгоритму матрица $$ A_ approx left(begin mathbf & 20.992347 & 24.701883 & 6.841640 \ 0 & -10.509149 & 12.631597 & 6.193862 \ 0 & -3.782749 & -2.013392 & -3.393084 \ 0 & 0.000165 & 0.003632 & mathbf_ end right) $$ имеет структуру близкую к верхней блочно-треугольной: $$ left(begin <color > & ast & ast & ast \ hline 0 & <color> & <color > & ast \ 0 & <color > & <color > & ast \ hline 0 & 0 & 0 & <color > end right) , . $$ Матрицы порядка $ 1 times 1 $, появившиеся на диагонали, соответствуют двум вещественным собственным числам матрицы $ A $. Матрица же второго порядка, стоящая на этой диагонали, имеет своими собственными числами пару комплексно-сопряженных собственных чисел матрицы $ A $. Так, полином $$ left|begin -10.509149 -lambda & 12.631597 \ -3.782749 & -2.013392 — lambda end right| = lambda^2+12.516007 lambda+ 69.270982 $$ имеет корнями $ -mathbf_ pm mathbf_ mathbf $. ♦
Для симметричных матриц такой ситуации не возникает. Более того, здесь матрица $ A_ $ будет диагональной, а матрица $$ prod_^ Q_j $$ при увеличении $ K $ будет состоять из столбцов, сколь угодно близким к собственным векторам
Сходимость к пределу у бесконечного произведения не гарантирована.
Пример. Вычислить $ A_ $ для матрицы
$$ A=left(begin 9 & 22 &-6\ 22 & -4 & 1 \ -6 & 1 & -7 end right) , . $$
Решение. $$ A_ approx left(begin mathbf_ & -0.252396 & 0\ -0.252396 & mathbf_ & 0\ 0 & 0 & mathbf end right) ; prod_^ Q_j approx left(begin -mathbf._ & -mathbf_ & mathbf\ -mathbf_ & mathbf_ & -mathbf \ mathbf_ & -mathbf_ & -mathbf end right) , . $$ Точность приближения последнего вектора существенно выше двух первых — близких по модулю. $$ prod_^ Q_j approx left(begin -mathbf_ & -mathbf_ & mathbf\ -mathbf_ & mathbf_ & -mathbf \ mathbf_ & -mathbf_ & -mathbf end right) , . $$ А вот $$ prod_^ Q_j $$ будет отличаться от предыдущей матрицы еще и сменой знаков у первых двух столбцов. ♦
При наличии близких по модулю вещественных корней, сходимость к $ A_ $ становится очень медленной.
Пример. Для матрицы
$$ A=left(begin 4 & -3 & 0 & 0 \ -3 & 10/3 & -5/3 & 0\ 0 & -5/3 & -33/25 & -68/75\ 0 & 0 & -68/75 & 149/75 end right) $$ имеем: $$ A_approx left(begin mathbf & 0 & 0 & 0 \ 0 & 0.159514 & -2.229578 & 0 \ 0 & -2.229578 & -0.088499 & 0.000004 \ 0 & 0 & 0.000004 & mathbf end right), $$ $$ A_approx left(begin mathbf & 0 & 0 & 0 \ 0 & 0.230166 & -2.229578 & 0 \ 0 & 2.224523 & -0.159152 & 0.000002 \ 0 & 0 & 0.000002 & mathbf end right) , . $$ Здесь два собственных числа однозначно локализуются на главной диагонали, но вот возникающие на ней же $ 2times 2 $ блоки совершенно друг на друга не похожи. Хотя, если на этих шагах остановить процесс и вычислить $$ left|begin 0.159514-lambda & -2.229578 \ -2.229578 & -0.088499-lambda endright| quad mbox quad left|begin 0.230166 -lambda & -2.229578 \ 2.2245235 & -0.159152 -lambda endright| $$ то эти два полинома оказываются практически идентичными, и их корни $ -2.197517 , 2.268531 $ совпадают с истинными значениями собственных чисел матрицы $ A $ с точностью до $ 10^ $. ♦
Видео:Собственные векторы и собственные числа линейного оператораСкачать

Источники
[1]. Хорн Р., Джонсон Ч. Матричный анализ. М.Мир.1989
Видео:Вычмат. ЛЭТИ. 2 курс. QR разложение для поиска собственных чиселСкачать
Реализация метода главных компонент на C#
Всем привет. На этой неделе в курсе по машинному обучению профессор Andrew Ng рассказал слушателям про метод главных компонент, с помощью которого можно уменьшить размерность пространства признаков ваших данных. Но к сожалению он не рассказал про метод вычисления собственных векторов и собственных чисел матрицы, просто сказал, что это сложно и посоветовал использовать матлаб/октавовскую функцию [U S V] = svd(a).
Для моего проекта мне понадобилась реализация этого метода на c#, чем я сегодня и занимался. Сам метод главных компонент очень элегантный и красивый, а если не понимать математику которая лежит за всем этим, то это можно это все назвать шаманством. Проблема вычисления собственных векторов матрицы в том, что не существует быстрого способа вычисления их точных значений, так что приходится выкручиваться. Я хочу рассказать об одном из таких способов выкрутиться, а так же приведу код на c# выполняющий эту процедуру. Прошу под кат.
Видео:A.7.33 Разложение матриц: QR, QL, RQ и LQ факторизации (переснято)Скачать

Метод главных компонент (пока без кода)
Часть первая: инициализация алгоритма. На вход алгоритму подается массив данных, а так же размерность пространства, до которой необходимо уменьшить данные.
- Вычисляется ковариационная матрица (у этой матрицы есть замечательное свойство — она симметричная, это нам очень пригодится)
- Вычисляются собственные вектора матрицы
- Выбираются первые эн собственных векторов, где эн это та самая размерность, до которой нужно уменьшить размерность пространства признаков; выбранные векторы можно записать вертикально и собрать в матрицу
Часть вторая: уменьшение размерности входного вектора. На вход подается вектор, размерности как и в массиве данных, использованном на шаге инициализации; на выходе вектор меньшей размерности (или проекция входного вектора на ортонормированный базис образованный выборкой из собственных векторов).
- Умножив скалярно входной вектор на все вектора из выборки собственных векторов, получается уменьшенный вектор:
Часть третья: восстановление размерность вектора (конечно же с потерей информации). На вход подается вектор размерности равной той, до которой мы уменьшали векторы; на выходе вектор исходной размерности.
- Если транспонировать матрицу
то в ней окажется столько же строк как и размерность входного вектора на предыдущем шаге, а искомый вектор восстанавливается по формуле:
Как видно вся вычислительная сложность находится в шаге инициализации при вычислении матрицы ковариации и собственных векторов. На вычислении ковариационной матрицы я не буду останавливаться, т.к. она вычисляется наивно по определению. Изучив несколько алгоритмов вычисления собственных векторов матрицы я остановился на итеративном методе QR декомпозиции. У него есть существенно ограничение, он выдает более менее точный результат только для симметричных матриц, но нам повезло :), матрица ковариации как раз именно такая. Вторым ограничение этого алгоритма является то, что матрица должна быть полноранговой.
Видео:А.7.35 Собственные вектора и собственные значения матрицыСкачать

QR декомпозиция
Итеративный QR метод поиска собственных векторов, очевидно использует QR разложение, так что для начала придется реализовать этот процесс. Для реализации этого процесса был выбран алгоритм Грэма-Шмидта.
Для этого нам понадобится функция, которая вычисляет проекцию вектора a на вектор b: 
Я не буду останавливаться на еще более простых функциях, типа ScalarVectorProduct, для того что бы размер кода в тексте не превысил критическую норму.
Итак собственно сама процедура QR разложения IList DecompositionGS(double[][] a) получает на вход матрицу, и выдает в ответ две матрицы:
- первая содержит в своих колонках ортонормированный базис, такой что
;
- вторая матрица будет верхней треугольной.
Первым делом мы разбиваем матрицу на столбцы и записываем их в список av:
Инициализируем два вспомогательных списка:
Это те самые одноименные списки, использующиеся на схеме алгоритма:
После инициализации, первые u и e у нас вычислены, продолжаем в цикле вычислять последующие значения:
И наконец формируем данные в выходном формате:
Ура! Теперь для этого нужен тест:
Функция Helper.AreEqualMatrices сравнивает поэлементно матрицы с точностью до третьего параметра.
Видео:Овчинников А. В. - Линейная алгебра - Собственные значения и собственные векторы линейного оператораСкачать

Итеративный QR метод
Итеративный QR метод основан на замечательной теореме, суть которой в том, что если инициализировать матрицу А ноль как и повторять следующий процесс бесконечно много раз:
а затем перемножить все полученные Q, то в результате получится матрица, в колонках которой будут собственные вектора исходной матрицы, значения которых будут тем точнее, чем дольше выполнялся процесс. Другими словами, при стремлении количества итераций к бесконечности, произведение будет стремиться к точным значениям собственных векторов. В то же время последняя будет на главной диагонали содержать собственные числа матрицы, приближенные конечно. Напоминаю что этот алгоритм более менее точно работает только для симметричных матриц.
Итак, метод QR итерации IList EigenVectorValuesExtractionQRIterative(double[][] a, double accuracy, int maxIterations) получает на вход по мимо самой матрицы, так же еще несколько параметров:
- double accuracy — точность которой мы хотим достичь, алгоритм остановится если изменения в значениях собственных векторов будут не более чем это значение;
- int maxIterations — максимальное количество итераций.
На выходе получаем две матрицы:
- первая содержит в своих колонках собственные векторы матрицы a;
- вторая матрица на своей главной диагонали содержит собственные значения матрицы a.
Итак начнем писать алгоритм, для начала создадим матрицы, которые будут содержать собственные векторы и собственные значения исходной матрицы:
И запустим цикл до остановки алгоритма:
Сформируем выходные данные:
И конечно же тест:
Стоит отметить, что собственные векторы могут менять направление от итерации к итерации, что будет видно по смене знаков их координат, но очевидно, что это не существенно.
Видео:ВСЕ ФИШКИ QR-КОДА: БОЛЬШОЙ РАЗБОРСкачать

Реализация метода главных компонент
Теперь все готово для имплементации сабжа статьи.
Скрытым параметром модели (класса) будет являться некоторое подмножество собственных векторов матрицы ковариации от исходных данных:
Конструктор принимает на вход массив данных и размерность, до которой следует уменьшить пространство признаков, а так же параметры для QR декомпозиции. Внутри вычисляется матрица ковариации и берутся первые несколько собственных векторов. Вообще существует способ выбрать оптимальное количество собственных векторов для нужного параметра потери информации, т.е. до какой размерности можно уменьшить пространство, потеряв при этом не более фиксированного процента информации, но я этот шаг опускаю, про него можно послушать в лекции Andrew Ng на сайте курса.
Затем реализуем прямое и обратное преобразование по формулам из начала статьи.
Видео:Интеллектуальная обработка данных 2024, лекция 16.01.2024, часть 2Скачать
Тестирование
Для тестирования придумаем небольшой массив данных, и проверяя на матлабе значения (используя код из домашки по PCA =), напишем класс для тестирования:
🎬 Видео
7 4 Собственные векторы и собственные значенияСкачать

Дети и деньги - Как обучать детей финансовой грамотности?Скачать

Как разложить вектор по базису - bezbotvyСкачать

7.1. Yet another base math: нормы, QR-разложениеСкачать

Спектральное разложение матрицСкачать

Собственные значения и собственные векторы. ПримерСкачать

#27. Сингулярное разложение и его связь с PCA | Машинное обучениеСкачать

Катруца А.М. - Математика для анализа данных. Часть 1 - Семинар 6. Разложение Шура и QR-алгоритм.Скачать