Пустой вектор в матлабе (8 видео) | Курс школьной геометрии

Пустой вектор в матлабе

Выше были рассмотрены операции с простыми переменными. Однако с их помощью сложно описывать сложные данные, такие как случайный сигнал, поступающий на вход фильтра или хранить кадр изображения и т.п. Поэтому в языках высокого уровня предусмотрена возможность хранить значения в виде массивов. В MatLab эту роль выполняют векторы и матрицы.

Ниже показан пример задания вектора с именем a, и содержащий значения 1, 2, 3, 4:

a = [1 2 3 4]; % вектор-строка

Для доступа к тому или иному элементу вектора используется следующая конструкция языка:

disp( a(1) ); % отображение значения 1-го элемента вектора
disp( a(2) ); % отображение значения 2-го элемента вектора
disp( a(3) ); % отображение значения 3-го элемента вектора
disp( a(4) ); % отображение значения 4-го элемента вектора

т.е. нужно указать имя вектора и в круглых скобках написать номер индекса элемента, с которым предполагается работать. Например, для изменения значения 2-го элемента массива на 10 достаточно записать

a(2) = 10; % изменение значения 2-го элемента на 10

Часто возникает необходимость определения общего числа элементов в векторе, т.е. определения его размера. Это можно сделать, воспользовавшись функцией length() следующим образом:

N = length(a); % (N=4) число элементов массива а

Если требуется задать вектор-столбец, то это можно сделать так

a = [1; 2; 3; 4]; % вектор-столбец

b = [1 2 3 4]’; % вектор-столбец

при этом доступ к элементам векторов осуществляется также как и для векторов-строк.

Следует отметить, что векторы можно составлять не только из отдельных чисел или переменных, но и из векторов. Например, следующий фрагмент программы показывает, как можно создавать один вектор на основе другого:

a = [1 2 3 4]; % начальный вектор a = [1 2 3 4]
b = [a 5 6]; % второй вектор b = [1 2 3 4 5 6]

Здесь вектор b состоит из шести элементов и создан на основе вектора а. Используя этот прием, можно осуществлять увеличение размера векторов в процессе работы программы:

a = [a 5]; % увеличение вектора а на один элемент

Недостатком описанного способа задания (инициализации) векторов является сложность определения векторов больших размеров, состоящих, например, из 100 или 1000 элементов. Чтобы решить данную задачу, в MatLab существуют функции инициализации векторов нулями, единицами или случайными значениями:

a1 = zeros(1, 100); % вектор-строка, 100 элементов с
% нулевыми значениями
a2 = zeros(100, 1); % вектор-столбец, 100 элементов с
% нулевыми значениями
a3 = ones(1, 1000); % вектор-строка, 1000 элементов с
% единичными значениями
a4 = ones(1000, 1); % вектор-столбец, 1000 элементов с
% единичными значениями
a5 = rand(1000, 1); % вектор-столбец, 1000 элементов со
% случайными значениями

Матрицы в MatLab задаются аналогично векторам с той лишь разницей, что указываются обе размерности. Приведем пример инициализации единичной матрицы размером 3х3:

E = [1 0 0; 0 1 0; 0 01]; % единичная матрица 3х3

E = [1 0 0
0 1 0
0 0 1]; % единичная матрица 3х3

Аналогичным образом можно задавать любые другие матрицы, а также использовать приведенные выше функции zeros(), ones() и rand(), например:

A1 = zeros(10,10); % нулевая матрица 10х10 элементов

A2 = zeros(10); % нулевая матрица 10х10 элементов
A3 = ones(5); % матрица 5х5, состоящая из единиц
A4 = rand(100); % матрица 100х100, из случайных чисел

Для доступа к элементам матрицы применяется такой же синтаксис как и для векторов, но с указанием строки и столбца где находится требуемый элемент:

A = [1 2 3;4 5 6;7 8 9]; % матрица 3х3
disp( A(2,1) ); % вывод на экран элемента, стоящего во
% второй строке первого столбца, т.е. 4
disp( A(1,2) ); % вывод на экран элемента, стоящего в
% первой строке второго столбца, т.е. 2

Также возможны операции выделения указанной части матрицы, например:

B1 = A(:,1); % B1 = [1; 4; 7] – выделение первого столбца
B2 = A(2,:); % B2 = [1 2 3] – выделение первой строки
B3 = A(1:2,2:3); % B3 = [2 3; 5 6] – выделение первых двух
% строк и 2-го и 3-го столбцов матрицы А.

Размерность любой матрицы или вектора в MatLab можно определить с помощью функции size(), которая возвращает число строк и столбцов переменной, указанной в качестве аргумента:

a = 5; % переменная а
A = [1 2 3]; % вектор-строка
B = [1 2 3; 4 5 6]; % матрица 2х3
size(a) % 1х1
size(A) % 1х3
size(B) % 2х3

Копирование информации со страницы разрешается только с указанием ссылки на данный сайт

Содержание

Создать массив нулей в MATLAB
1. Создание массива нулей вручную
2. Создание массива нулей с помощью встроенной функции (zeros ())
Создание (nxn) матрицы нулей
Создание массива нулей (sz1 by sz2 by- …….-Szn)
Создание матрицы определенного размера
Создание указанных типов данных нулей
Создание матрицы с использованием прототипа массива
colon , :
Syntax
Description
📸 Видео

Видео:Matlab создание вектора данныхСкачать

Создать массив нулей в MATLAB

MATLAB обычно хранит свои переменные в матричной форме, а также в виде массива и вектора. Иногда нам часто требуется матрица (или массив, или вектор) нуля (ов) для некоторых конкретных операций. Мы можем создать матрицу нулей (ей) вручную или с помощью встроенной функции MATLAB. Встроенная функция, которая используется для создания массива или матрицы нулей (ей), называется функцией zeros (). Обычно мы предпочитаем эту встроенную функцию для простоты задачи, а не создавать массив нулей вручную. Следующая часть содержит два метода создания массива или матрицы нулей.

Видео:MATLAB 04 Массивы и матрицыСкачать

1. Создание массива нулей вручную

Если мы хотим создать массив нулей, мы можем просто сделать это вручную, используя следующий код:

Matlab

По сути, это вектор-строка размером 1X5, а также массив из 5 нулей.

Создание вектора-столбца вручную: если мы хотим создать вектор-столбец, мы можем просто использовать следующий код:

Matlab

По сути, он создает вектор-столбец размером 5X1.

Создание (nxm) матрицы нулей: В этом разделе мы собираемся создать размерную матрицу (nxm). Например, пусть n = 3 и m = 4. По сути, следующая строка кода сгенерирует матрицу с 3 строками и 4 столбцами.

Matlab

Видео:Работа с массивами. Вектор столбцы и вектор строки 1. Урок 7Скачать

2. Создание массива нулей с помощью встроенной функции (zeros ())

Есть несколько матриц и массивов, которые мы можем создать с помощью функции zeros (). Мы собираемся подробно описать каждый из них в следующем разделе:

Создание скалярного нуля

Синтаксис: имя_переменной = нули

Возвращаемое значение: в этом случае возвращаемое значение — только скалярный ноль («0»).

Matlab

Создание (nxn) матрицы нулей

синтаксис: matrix = zeros (n) // Здесь n — размер матрицы.

Возвращаемое значение: функция zeros (n) возвращает матрицу нулей (nxn):

Размер квадратной матрицы, заданной как целое число.
Если n равно 0, возвращается пустая матрица.
Если n отрицательно, он также возвращает пустую матрицу.

Matlab

Этот код возвращает матрицу нулей 3×3.

Создание массива нулей (sz1 by sz2 by- …….-Szn)

синтаксис: матрица = нули (sz1, sz2, ……., szn)

Возвращаемое значение: эта функция возвращает массив нулей размером sz1 на… на szN, где sz1,…, szN указывают размер каждого измерения. Например, zeros (2, 3, 4) возвращает матрицу нулей 2 X 3 X 4.

Все входные аргументы указаны как целое число.
Если любой из аргументов равен 0, возвращается пустая матрица.
Если какой-либо из аргументов отрицательный, он обрабатывается как 0.
За пределами второго измерения zeros () игнорирует конечные измерения с размером 1. Например, нули (4,1,1, 1) создают вектор нулей 4 на 1.

Matlab

Приведенный выше код создает массив нулей размером 2 на 3 на 4.

Создание матрицы определенного размера

Синтаксис: matrix = zeros (sz) // Здесь sz — размер матрицы в форме [mn].

Возвращаемое значение: возвращает массив нулей, где вектор размера sz определяет размер (матрицу). Например, нули ([2 3]) возвращают матрицу 2 на 3.

Размер каждого измерения, заданного как вектор-строка целочисленных значений. Остальные характеристики этого синтаксиса такие же, как и у предыдущего.

Matlab

% MATLAB Code for clone the size of

% another matrix

matrix = zeros([2 3])

Или мы также можем клонировать размер другой матрицы, например:

Matlab

Приведенный выше код в основном возвращает матрицу 2 X 3 с нулями в качестве каждого элемента.

Создание указанных типов данных нулей

синтаксис: matrix = zeros (___, typename) // Здесь первым аргументом может быть любой из предыдущих типов.

Возвращаемое значение: возвращает массив нулей указанного типа данных с именем typename.

Тип данных (класс) для создания, указанный как ’double’, ’single’, ’logic’, ’int8′, ’uint8′, ’int16′, ’uint16′, ’int32′, ’uint32′, ’int64′, uint64 или имя другого класса, который поддерживает нули.

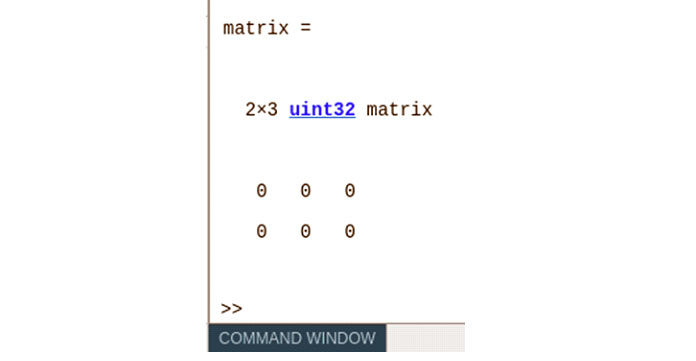
Matlab

Этот код создает матрицу размером 2 на 3 с типом данных uint32.

Создание матрицы с использованием прототипа массива

синтаксис: matrix = zeros (___, ’like’, p) // Здесь первым аргументом может быть любой из предыдущих типов.

Возвращаемое значение: возвращает массив нулей, например p; т. е. того же типа данных (класса), разреженности и сложности (реальной или сложной), что и p. Пользователь может указать typename или like, но не то и другое одновременно.

Прототип создаваемого массива, заданного как массив.

Видео:Основы линейной алгебры. 2. Векторы. Часть 1Скачать

colon , :

Vector creation, array subscripting, and for -loop iteration

Видео:Поэлементные операции с векторами. Работа с массивами. Урок 11Скачать

Syntax

Видео:Символьные переменные и функции. Матрицы и векторы. Урок 142Скачать

Description

The colon is one of the most useful operators in MATLAB ® . It can create vectors, subscript arrays, and specify for iterations.

x = j : k creates a unit-spaced vector x with elements [j,j+1,j+2. j+m] where m = fix(k-j) . If j and k are both integers, then this is simply [j,j+1. k] .

x = j : i : k creates a regularly-spaced vector x using i as the increment between elements. The vector elements are roughly equal to [j,j+i,j+2*i. j+m*i] where m = fix((k-j)/i) . However, if i is not an integer, then floating point arithmetic plays a role in determining whether colon includes the endpoint k in the vector, since k might not be exactly equal to j+m*i . If you specify nonscalar arrays, then MATLAB interprets j:i:k as j(1):i(1):k(1) .

x = colon(j,k) and x = colon(j,i,k) are alternate ways to execute the commands j:k and j:i:k , but are rarely used. These syntaxes enable operator overloading for classes.

A(:,n) , A(m,:) , A(:) , and A(j:k) are common indexing expressions for a matrix A that contain a colon. When you use a colon as a subscript in an indexing expression, such as A(:,n) , it acts as shorthand to include all subscripts in a particular array dimension. It is also common to create a vector with a colon for the purposes of indexing, such as A(j:k) . Some indexing expressions combine both uses of the colon, as in A(:,j:k) .

Common indexing expressions that contain a colon are:

A(:,n) is the n th column of matrix A .

A(m,:) is the m th row of matrix A .

A(. p) is the p th page of three-dimensional array A .

A(:) reshapes all elements of A into a single column vector. This has no effect if A is already a column vector.

A(. ) reshapes all elements of A into a two-dimensional matrix. This has no effect if A is already a matrix or vector.

A(j:k) uses the vector j:k to index into A and is therefore equivalent to the vector [A(j), A(j+1), . A(k)] .

A(:,j:k) includes all subscripts in the first dimension but uses the vector j:k to index in the second dimension. This returns a matrix with columns [A(:,j), A(:,j+1), . A(:,k)] .