С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), выберите вид уравнения (канонический, параметрический, общий (для двухмерного пространства)), введите данные в ячейки и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
- Предупреждение
- 1. Угол между прямыми на плоскости
- Прямые заданы каноническими уравнениями
- 1.1. Определение угла между прямыми
- 1.2. Условие параллельности прямых
- 1.3. Условие перпендикулярности прямых
- Прямые заданы общими уравнениями
- 1.4. Определение угла между прямыми
- 1.5. Условие параллельности прямых
- 1.6. Условие перпендикулярности прямых
- 2. Угол между прямыми в пространстве
- 2.1. Определение угла между прямыми
- 2.2. Условие параллельности прямых
- 2.3. Условие перпендикулярности прямых
- Угол между прямыми
- Определение угла между прямыми
- Угол между прямыми на плоскости
- Угол между прямыми заданными уравнениями с угловым коэффициентом
- Угол между прямыми через направляющие векторы этих прямых
- Угол между прямыми через векторы нормалей этих прямых
- Угол между прямыми через направляющий вектор и вектор нормали этих прямых
- Примеры задач на вычисления угла между прямыми на плоскости
- Угол между прямыми в пространстве
- Взаимное расположение прямых на плоскости. Угол между прямыми на плоскости. Расстояние от точки до прямой на плоскости
- 📹 Видео
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

1. Угол между прямыми на плоскости
Прямые заданы каноническими уравнениями
1.1. Определение угла между прямыми
Пусть в двухмерном пространстве прямые L1 и L2 заданы каноническими уравнениями
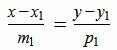 , , | (1.1) |
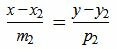 , , | (1.2) |
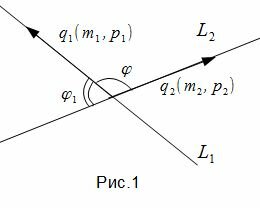
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 (рис.1).
 , , |
 , , | (1.3) |
Из выражения (1.3) получим:
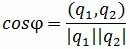 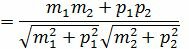 . . | (1.4) |
Таким образом, из формулы (1.4) можно найти угол между прямыми L1 и L2. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ1. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
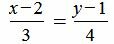 . . | (1.5) |
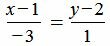 . . | (1.6) |
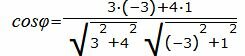 . . |
Упростим и решим:
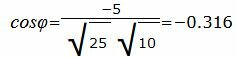 . . |
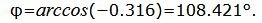 |
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
 |
Угол между прямыми равен:
 |
1.2. Условие параллельности прямых
Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:
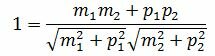 . . | (1.7) |
Сделаем преобразования с выражением (1.7):
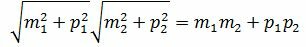 , , |
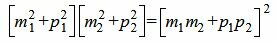 , , |
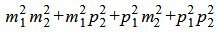 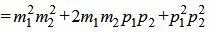 , , |
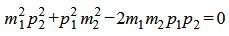 , , |
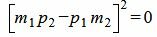 , , |
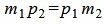 . . | (1.8) |
Таким образом условие параллельности прямых L1 и L2 имеет вид (1.8). Если m2≠0 и p2≠0, то (1.8) можно записать так:
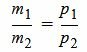 . . | (1.9) |
Пример 2. Определить, параллельны ли прямые
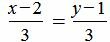 . . | (1.10) |
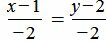 . . | (1.11) |
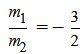 , , 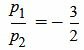 . . |
Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.
Ответ. Прямые (1.10) и (1.11) параллельны.
1.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:
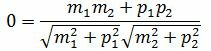 . . | (1.12) |
Правая часть выражения (1.12) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
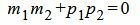 . . | (1.13) |
Пример 3. Определить, перпендикулярны ли прямые
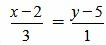 | (1.14) |
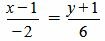 . . | (1.15) |
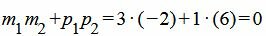 . . | (16) |
Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.
Ответ. Прямые (1.14) и (1.15) перпендикулярны.
Прямые заданы общими уравнениями
1.4. Определение угла между прямыми
Пусть две прямые L1 и L2 заданы общими уравнениями
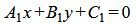 | (1.17) |
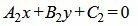 . . | (1.18) |
Так как нормальным вектором прямой L1 является n1=(A1, B1), а нормальным вектором прямой L2 является n2=(A2, B2), то задача об определении угла между прямыми L1 и L2 сводится к определению угла φ между векторами n1 и n2 (Рис.2).
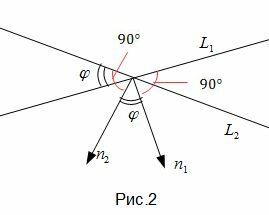 . . |
Из определения скалярного произведения двух векторов, имеем:
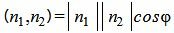 . . | (1.19) |
Из уравнения (19) получим
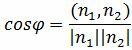 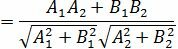 . . | (1.20) |
Пример 4. Найти угол между прямыми
| 5x1−2x2+3=0 | (1.21) |
| x1+3x2−1=0. | (1.22) |
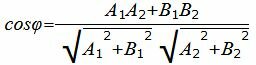 | (23) |
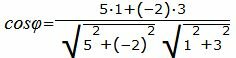 |
Упростим и решим:
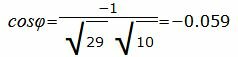 |
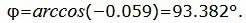 |
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
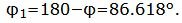 |
1.5. Условие параллельности прямых
Так как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:
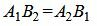 . . | (1.24) |
С другой стороны условие параллельности прямых L1 и L2 эквивалентно условию коллинеарности векторов n1 и n2 и можно представить так:
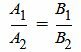 . . | (1.25) |
Как видим уравнения (1.24) и (1.25) эквивалентны при A2≠0 и B2≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24).
Пример 5. Определить, параллельны ли прямые
| 4x+2y+2=0 | (1.26) |
Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.
Ответ. Прямые (1.26) и (1.27) параллельны.
1.6. Условие перпендикулярности прямых
Условие перпендикулярности прямых L1 и L2 можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n1,n2)=0. Откуда
| A1A2+B1B2=0. | (1.28) |
Таким образом условие перпендикулярности прямых определяется равенством (1.28).
Пример 6. Определить, перпендикулярны ли прямые
| 4x−1y+2=0 | (1.29) |
| 2x+8y−14=0. | (1.30) |
Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.
Ответ. Прямые (1.29) и (1.30) перпендикулярны.
Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

2. Угол между прямыми в пространстве
2.1. Определение угла между прямыми
Пусть в пространстве прямые L1 и L2 заданы каноническими уравнениями
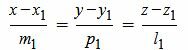 , , | (2.1) |
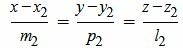 , , | (2.2) |
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 .
 , , | (2.3) |
Из выражения (2.3) получим:
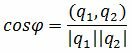 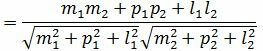 . . | (2.4) |
Таким образом, из формулы (2.4) можно найти угол между прямыми L1 и L2. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
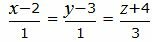 . . | (2.5) |
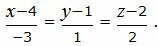 | (2.6) |
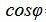 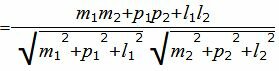 . . |
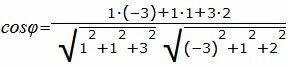 . . |
Упростим и решим:
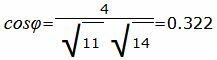 . . |
 |
Угол между прямыми равен:
 |
2.2. Условие параллельности прямых
Условие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q1 и q2, т.е. соответствующие координаты этих векторов пропорциональны. Пусть
| m1=αm2, p1=αp2, l1=αl2 | (2.7) |
где α − некоторое число. Тогда соответствующие координаты векторов q1 и q2 пропорциональны, и, следовательно прямые L1 и L2 параллельны.
Условие параллельности прямых можно представить и так:
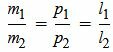 | (2.8) |
Отметим, что любую пропорцию 
Пример 2. Определить, параллельны ли прямые
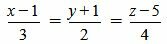 . . | (2.9) |
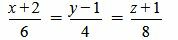 . . | (2.10) |
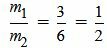 , , 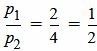 , , 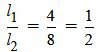 . . |
Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.
Ответ. Прямые (2,9) и (2,10) параллельны.
Пример 3. Определить, параллельны ли прямые
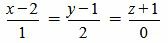 . . | (2.11) |
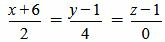 . . | (2.12) |
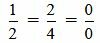 . . | (2.13) |
Выражение (2.13) нужно понимать так:
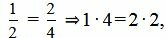 , , 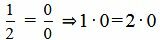 , , 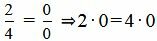 . . | (2.14) |
Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.
Ответ. Прямые (2.11) и (2.12) параллельны.
2.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:
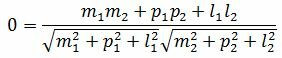 . . | (2.15) |
Правая часть выражения (2.15) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
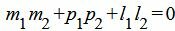 . . | (2.16) |
Пример 3. Определить, перпендикулярны ли прямые
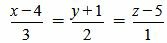 | (2.17) |
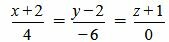 . . | (2.18) |
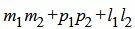 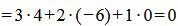 . . | (2.19) |
Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.
Ответ. Прямые (2.17) и (2.18) перпендикулярны.
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Угол между прямыми
Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Определение угла между прямыми
Видео:Параллельность прямых. 10 класс.Скачать

Угол между прямыми на плоскости
Угол между прямыми заданными уравнениями с угловым коэффициентом
то угол между ними можно найти, используя формулу:
Если знаменатель равен нулю (1 + k 1· k 2 = 0), то прямые перпендикулярны.
Соответственно легко найти угол между прямыми
tg γ = tg ( α — β ) = tg α — tg β 1 + tg α ·tg β = k 1 — k 2 1 + k 1· k 2
Угол между прямыми через направляющие векторы этих прямых
cos φ = | a · b | | a | · | b |
Если уравнение прямой задано параметрически
x = l t + a y = m t + b
то вектор направляющей имеет вид
Если уравнение прямой задано как
то для вычисления направляющего вектора, можно взять две точки на прямой.
Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = — C B значит точка на прямой имеет координаты K(0, — C B ), при y = 0 => x = — C A значит точка на прямой имеет координаты M(- C A , 0). Вектор направляющей KM = .
Если дано каноническое уравнение прямой
то вектор направляющей имеет вид
Если задано уравнение прямой с угловым коэффициентом
то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b ), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b ). Вектор направляющей KM =
Угол между прямыми через векторы нормалей этих прямых
cos φ = | a · b | | a | · | b |
Если уравнение прямой задано как
то вектор нормали имеет вид
Если задано уравнение прямой с угловым коэффициентом
то вектор нормали имеет вид
Угол между прямыми через направляющий вектор и вектор нормали этих прямых
sin φ = | a · b | | a | · | b |
Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Примеры задач на вычисления угла между прямыми на плоскости
Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:
tg γ = k 1 — k 2 1 + k 1· k 2 = 2 — (-3) 1 + 2·(-3) = 5 -5 = 1
Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.
Для первой прямой направляющий вектор , для второй прямой направляющий вектор
cos φ = |1 · 2 + 2 · 1| 1 2 + 2 2 · 2 2 + 1 2 = 4 5 · 5 = 0.8
Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.
Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.
2 x + 3 y = 0 => y = — 2 3 x ( k 1 = — 2 3 )
x — 2 3 = y 4 => y = 4 3 x — 8 3 ( k 2 = 4 3 )
tg γ = k 1 — k 2 1 + k 1· k 2 = — 2 3 — 4 3 1 + (- 2 3 )· 4 3 = — 6 3 1 — 8 9 = 18
Видео:Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

Угол между прямыми в пространстве
cos φ = | a · b | | a | · | b |
Если дано каноническое уравнение прямой
то направляющий вектор имеет вид
Если уравнение прямой задано параметрически
x = l t + a y = m t + b z = n t + c
то направляющий вектор имеет вид
Решение: Так как прямые заданы параметрически, то — направляющий вектор первой прямой, направляющий вектор второй прямой.
cos φ = |2 · 1 + 1 · (-2) + (-1) · 0| 2 2 + 1 2 + (-1) 2 · 1 2 + (-2) 2 + 0 2 = 0 6 · 5 = 0
Решение: Для решения этой задачи найдем направляющие векторы этих прямых.
Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор .
Преобразуем второе уравнение к каноническому вид.
1 — 3 y = 1 + y -1/3 = y — 1/3 -1/3
3 z — 5 2 = z — 5/3 2/3
Получено уравнение второй прямой в канонической форме
x — 2 -2 = y — 1/3 -1/3 = z — 5/3 2/3
— направляющий вектор второй прямой.
cos φ = 3·(-2) + 4·(- 1 3 ) + 5· 2 3 3 2 + 4 2 + 5 2 · (-2) 2 + (- 1 3 ) 2 + ( 2 3 ) 2 = -6 — 4 3 + 10 3 9 + 16 + 25 · 4 + 1 9 + 4 9 = -4 50 · 41/9 = 12 5 82 = 6 82 205
Видео:Теорема 13.2 Если две прямые параллельны третьей, то они параллельны ||Геометрия 7 класс||Скачать

Взаимное расположение прямых на плоскости. Угол между прямыми на плоскости. Расстояние от точки до прямой на плоскости
ПРЯМАЯ НА ПЛОСКОСТИ
Взаимное расположение прямых на плоскости. Угол между прямыми на плоскости. Расстояние от точки до прямой на плоскости
Показать, при каких условиях прямые на плоскости параллельны, пересекаются, совпадают. Рассмотреть случаи, когда прямые заданы каноническими, общими или уравнениями с угловым коэффициентом. Научить находить косинус угла между пересекающимися прямыми и координаты точки их пересечения. Научить находить расстояние от точки до прямой на плоскости и расстояние между параллельными прямыми.
1) Школьники должны знать:
− условия, при которых прямые пересекаются, параллельны, совпадают, в случаях, если прямые заданы общими уравнениями, каноническими, уравнениями с угловым коэффициентом;
− условия, при которых прямые перпендикулярны;
− формулу для нахождения расстояния от точки до прямой на плоскости;
− формулу для нахождения косинуса угла между пересекающимися прямыми в случаях, если прямые заданы общими уравнениями, каноническими, уравнениями с угловым коэффициентом.
2) Школьники должны уметь:
− выяснять взаимное расположение прямых на плоскости;
− находить угол между прямыми на плоскости;
− находить расстояние от точки до прямой на плоскости;
− находить расстояние между параллельными прямыми на плоскости.
Взаимное расположение прямых на плоскости
Прямые на плоскости могут совпадать, пересекаться или быть параллельными.
1.Пусть на плоскости заданы общими уравнениями две прямые L1 и L2:
где 

а) совпадают, если
− нормальные векторы прямых коллинеарны, а значит, их координаты пропорциональны;
− точка, лежащая на первой прямой, лежит также и на второй прямой

б) параллельны, если
− нормальные векторы прямых коллинеарны, а значит, их координаты пропорциональны;
− точка, лежащая на первой прямой, не лежит на второй прямой.

в) пересекаются, если нормальные векторы прямых не коллинеарны, а значит, их координаты не пропорциональны, т. е.

2.Пусть на плоскости заданы прямые L1 и L2 каноническими уравнениями:
а) совпадают, если
− направляющие векторы прямых коллинеарны, а значит, их координаты пропорциональны;
− точка, лежащая на первой прямой, лежит также и на второй прямой


б) параллельны, если
− направляющие векторы прямых коллинеарны, а значит, их координаты пропорциональны;
− точка, лежащая на первой прямой, не лежит на второй прямой.


в) пересекаются, если направляющие векторы прямых не коллинеарны, а значит, их координаты не пропорциональны, т. е.
3.Если прямые L1 и L2 заданы уравнениями с угловым коэффициентом
а) совпадают, если k1 = k2 и b1 = b2;
б) параллельны, если k1 = k2 и b1 ¹ b2;
в) пересекаются, если k1 ¹ k2.
Угол между прямыми на плоскости
Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при пересечении прямых.
1.Пусть на плоскости заданы прямые L1 и L2 общими уравнениями:
Тогда косинус наименьшего угла между прямыми L1 и L2 на плоскости равен модулю косинуса угла между нормальными векторами этих прямых:
В случае если прямые L1 и L2 перпендикулярны, их нормальные векторы также перпендикулярны, а значит, скалярное произведение нормальных векторов должно быть равно нулю, т. е. 
2.Пусть прямые L1 и L2 заданы каноническими уравнениями:
Тогда косинус наименьшего угла между прямыми L1 и L2 равен модулю косинуса угла между направляющими векторами этих прямых:
2. Пусть прямые L1 и L2 заданы уравнениями с угловым коэффициентом
Тогда тангенс наименьшего угла между прямыми L1 и L2 можно найти по формуле:

где k1 и k2 – угловые коэффициенты прямых L1 и L2.
Очевидно, что две прямые будут параллельны, если их угловые коэффициенты будут равны.
Итак, условие параллельности двух прямых:
Если две прямые перпендикулярны, т. е. угол φ = p/2, мы получим
Это будет иметь место, когда
Итак, условие перпендикулярности двух прямых:
Расстояние от точки до прямой на плоскости
Расстояние от точки до прямой, не содержащей эту точку, есть длина перпендикуляра, проведенного из этой точки на прямую.
Расстояние от точки до прямой можно вычислить:
1) Как длину отрезка перпендикуляра, если удается включить этот отрезок в некоторый треугольник в качестве одной из высот;
2) Используя координатно – векторный метод.
Пусть на плоскости заданы прямая L и точка M, не принадлежащая этой прямой

расстояние от точки М0(x0, y0) до прямой L.
Замечание. Расстояние между двумя параллельными прямыми на плоскости можно найти по последней формуле, если находить расстояние от любой точки, принадлежащей одной прямой, до другой прямой.
Даны координаты точек A(4, 1), B(2, −1), C(−3, 5). Найти угол между медианой и высотой, проведенными из вершины A.
Напишем уравнение высоты AH. Для любой точки M(x, y), лежащей на прямой AH, вектор 




Итак, уравнение высоты AH:
Напишем уравнение медианы, проведенной из вершины A. Найдем координаты точки D. Точка D − середина отрезка BC, значит, ее координаты можно найти как среднее арифметическое координат точек B и C. Координаты точек B(2, −1) и C(−3, 5), тогда координаты точки D:
Для любой точки N(x, y), лежащей на медиане AD, вектор 



Запишем условие пропорциональности координат:

По свойству пропорций получим:

Получили общее уравнение медианы AD:

Косинус наименьшего угла между прямыми равен модулю косинуса угла между нормальными векторами этих прямых.
Уравнение прямой AH: 




Ответ: 
Даны координаты точек A(4, 1), B(2, −1), C(−3, 5). Найти расстояние от точки A до прямой BC.
Напишем уравнение прямой BC. Для любой точки N(x, y), лежащей на прямой BC, вектор 


Перемножив по свойству пропорций, перейдем к общему уравнению прямой:
Тогда общее уравнение прямой BC:

Точка A(4, 1) 



Ответ: расстояние от точки A до прямой BC равно 
Выяснить взаимное расположение прямых L1 и L2. Если прямые пересекаются, то найти угол между ними и координаты точки их пересечения, а если параллельны, то найти расстояние между ними:
L1: 
L2: 
Запишем координаты нормальных векторов прямых L1 и L2:
L1: 

L2: 

Найдем отношение координат нормальных векторов прямых:

Так как координаты нормальных векторов пропорциональны, то векторы 

Прямые параллельны так как

Расстояние между прямыми найдем, как расстояние от точки М1, лежащей на прямой L1, до прямой L2 по формуле:


Найдем координаты точки M1, принадлежащей прямой L1. Для этого одну из координат, например y0, примем равной нулю, тогда x0 = 4, значит, точка 
Ответ: прямые параллельны, расстояние между ними равно 
Выяснить взаимное расположение прямых L1 и L2. Если прямые пересекаются, то найти угол между ними и координаты точки их пересечения, а если параллельны, то найти расстояние между ними:
Найдем направляющие векторы прямых L1 и L2:

то координаты направляющих векторов не пропорциональны. Следовательно, прямые L1 и L2 пересекаются.
Косинус наименьшего угла между прямыми равен модулю косинуса угла между направляющими векторами этих прямых.
Найдем координаты точки пересечения прямых L1 и L2. Для этого получим общие уравнения этих прямых.
Пусть точка М (x0, y0) − точка пересечения прямых L1 и L2. Тогда координаты точки М должны удовлетворять обоим уравнениям. Решим систему уравнений:
Следовательно, точка 
Ответ: прямые пересекаются, 

Задачи для усвоения пройденного материала.
1. Найти расстояние от точки А(−4, 1) до прямой, проходящей через точки B(1, −1), C(1, 5).
2. Выяснить взаимное расположение прямых 

3. Найти точку пересечения медиан треугольника, вершинами которого являются точки
4. Найти точку пересечения высот треугольника, вершинами которого являются точки
5. Написать уравнение прямой, проходящей через точку 

6. Найти угол между прямыми 
1. При каких значениях параметров прямые 

2. При каких значениях параметров прямые 

3. При каких значениях параметров прямые 

4. Как найти угол между пересекающимися прямыми,?
5. Как найти координаты точки пересечения прямых?
6. Как найти расстояние между параллельными прямыми?
7. При каких значениях параметров прямые 

📹 Видео
Параллельные прямые. 6 класс.Скачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Параллельность прямой и плоскости. 10 класс.Скачать

10 класс, 5 урок, Параллельность трех прямыхСкачать

Параллельные прямые — Признак Параллельности Прямых и Свойства УгловСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

🔴 Найдите sinx, если cosx=-√15/4 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 5 | ШКОЛА ПИФАГОРАСкачать

№44. Прямые ОВ и CD параллельные, а ОА и CD — скрещивающиеся прямые.Скачать

Задача, которую боятсяСкачать

Геометрия. 7 класс. Параллельные прямые, их признаки и свойства /14.01.2021/Скачать




















































