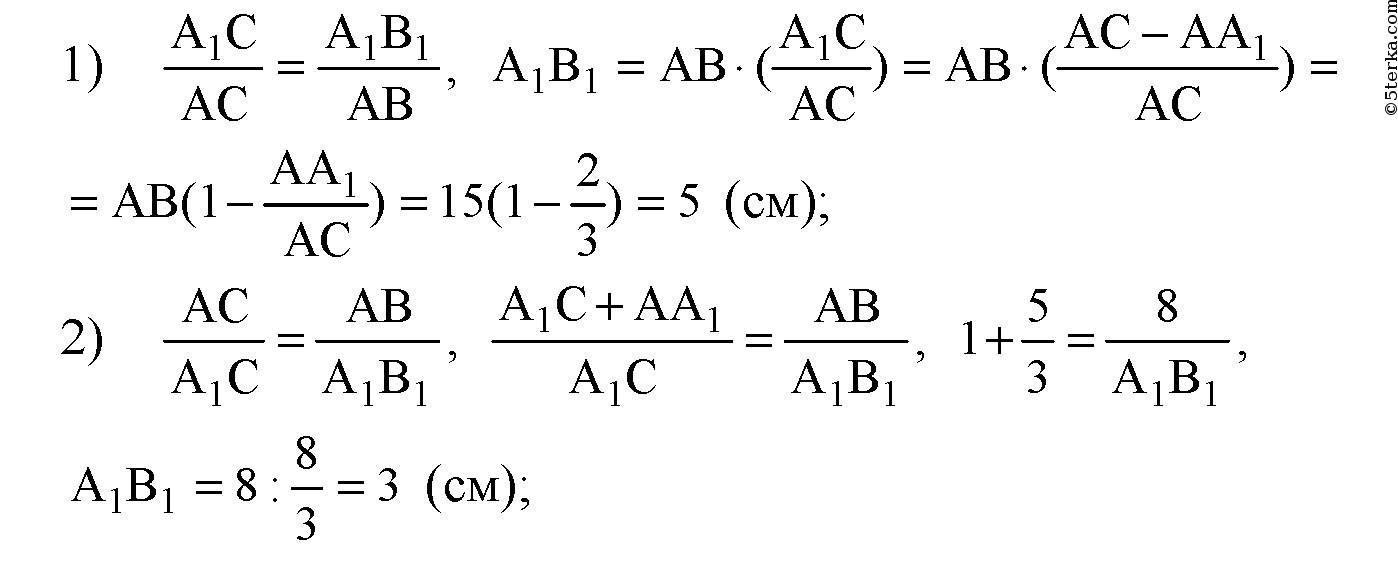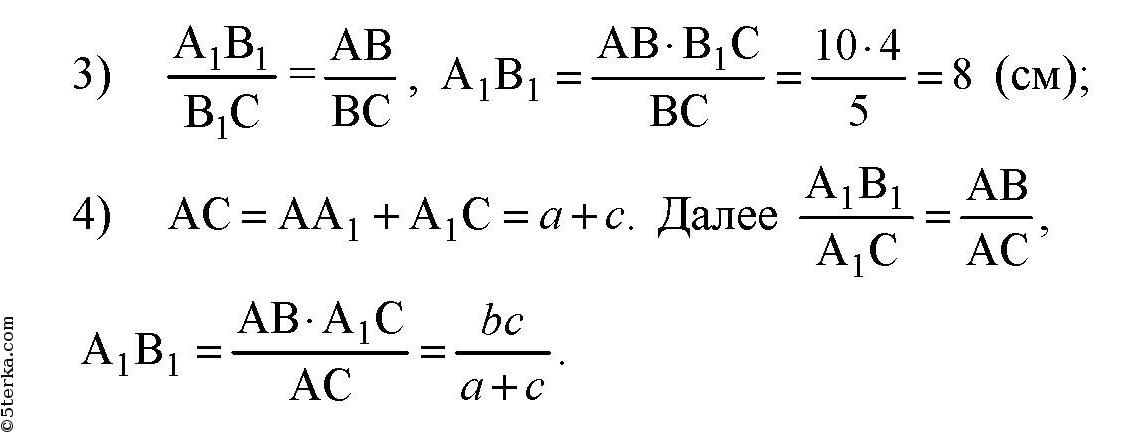Прямые а1с1 а2с2 а3с3 параллельны стороне ас треугольника авс

Разделы: Математика

Цель:

• повторить и обобщить изученные теоремы;
• рассмотреть их применение при решении ряда задач;
• подготовка учащихся к вступительным экзаменам в ВУЗы;
• воспитывать эстетическое выполнение чертежей к задачам.

Оборудование: мультимедийный проектор. Приложение 1.

1. Организационный момент.

2. Проверка домашнего задания:

• доказательство теорем – 2 учащихся + 2 уч-ся – консультанты (проверяющие);
• решение домашних задач – 3 учащихся;
• работа с классом – устное решение задач:

Точка С₁ делит сторону АВ треугольника АВС в отношении 2 : 1. точка В₁ лежит на продолжении стороны АС за точку С, и АС = СВ₁. В каком отношении делит прямая В₁ С₁ сторону ВС? (на слайде 2).

Решение: По условиюИспользуя теорему Менелая, находим: .

В треугольнике АВС АD – медиана, точка О – середина медианы. Прямая ВО пересекает сторону АС в точке К.

В каком отношении точка К делит АС, считая от точки А? (на слайде 3).

Решение: Пусть ВD = DС = а, АО = ОD = m. Прямая ВК пересекает две стороны и продолжение третьей стороны треугольника АDС . По теореме Менелая .

В треугольнике АВС на стороне ВС взята точка N так, что NС = 3ВN; на продолжении стороны АС за точку А взята точка М так, что МА = АС. Прямая МN пересекает сторону АВ в точке F. Найдите отношение . (на слайде 4).

Решение: По условию задачи МА = АС, NС = 3 ВN. Пусть МА = АС = b, BN = k, NC = 3k. Прямая МN пересекает две стороны треугольника АВС и продолжение третьей. По теореме Менелая

.

На стороне PQ треугольника PQR взята точка N, а на стороне РR – точка L, причем NQ = LR. Точка пересечения отрезков QL и NR делит QR в отношении m : n, считая от точки Q. Найдите PN : PR. (на слайде 5).

Решение: По условию NQ = LR, . Пусть NA = LR = a, QF =km, LF = kn. Прямая NR пересекает две стороны треугольника PQL и продолжение третьей. По теореме Менелая

.

3. Отработка практических навыков.

1. Решение задач:

Докажите теорему: Медианы треугольника пересекаются в одной точке; точка пересечения делит каждую из них в отношении 2 : 1, считая от вершины. (рисунок 1 слайд 6).

Доказательство: Пусть АМ₁, ВМ₂, СМ₃ – медианы треугольника АВС. Чтобы доказать, что эти отрезки пересекаются в одной точке, достаточно показать, что Тогда по теореме Чевы (обратной) отрезки АМ₁, ВМ₂ и СМ₃ пересекаются в одной точке. Имеем:

Итак, доказано, что медианы треугольника пересекаются в одной точке.

Пусть О – точка пересечения медиан. Прямая М₃С пересекает две стороны треугольника АВМ₂ и продолжение третьей стороны этого треугольника. По теореме Менелая

или .

Рассматривая теорему Менелая для треугольников АМ₁С и АМ₂С, мы получаем, что

. Теорема доказана.

Докажите теорему: Биссектрисы треугольника пересекаются в одной точке. (рисунок 2 слайд 6).

Доказательство: Достаточно показать, что . Тогда по теореме Чевы (обратной) AL_1, BL_2, CL₃ пересекаются в одной точке. По свойству биссектрис треугольника:

. Перемножая почленно полученные равенства, получаем: . Итак, для биссектрис треугольника равенство Чевы выполняется, следовательно, они пересекаются в одной точке. Теорема доказана.

Докажите теорему: Высоты остроугольного треугольника пересекаются в одной точке. (рисунок 3 слайд 6).

Доказательство: Пусть АН₁, АН_2, АН₃ – высоты треугольника АВС со сторонами a, b, c. Из прямоугольных треугольников АВН₂ и ВСН₂ по теореме Пифагора выразим, соответственно, квадрат общего катета ВН₂, обозначив АН₂ = х, СН₂ = b – х.

(ВН₂) 2 = с 2 – х 2 и (ВН₂) 2 = а 2 – (b – х) 2 . приравнивая правые части полученных равенств, получаем с 2 – х 2 = а 2 – (b – х) 2 , откуда х = .

Тогда b –x = b — = .

Итак, АН₂ = , СН₂ = .

Аналогично рассуждая для прямоугольных треугольников АСН₂ и ВСН₃, ВАН₁ и САН₁, получим АН₃ = , ВН₃ = и ВН₁ = ,

СН₁ = .

Для доказательства теоремы достаточно показать, что . Тогда по теореме Чевы (обратной) отрезки АН₁, ВН₂ и СН₃ пересекаются в одной точке. Подставив в левую часть равенства выражения длин отрезков АН₃, ВН₃, ВН₁, СН₁, СН₂ и АН₂ через а, b, с, убеждаемся, что равенство Чевы для высот треугольника выполняется. Теорема доказана.

Задачи 5 – 7 самостоятельное решение 3 учащихся. (чертежи на экране).

2. остальные:

Докажите теорему: Если в треугольник вписана окружность, то отрезки, соединяющие вершины треугольника с точками касания противоположных сторон пересекаются в одной точке. (на рисунке 4 слайд 6).

Доказательство: Пусть А₁, В₁ и С₁ – точки касания вписанной окружности треугольника АВС. Для того, чтобы доказать, что отрезки АА₁, ВВ₁ и СС₁ пересекаются в одной точке, достаточно показать, что выполняется равенство Чевы:

. Используя свойство касательных, проведенных из одной точки, введем обозначения: ВС₁ = ВА₁ = х, СА₁ = СВ₁ = у, АВ₁ = АС₁ = z.

. Равенство Чевы выполняется, значит, указанные отрезки (биссектрисы треугольника) пересекаются в одной точке. Эту точку называют точкой Жергона. Теорема доказана.

3. Разбор задач 5, 6, 7.

Пусть АD – медиана треугольника АВС. На стороне АD взята точка К так, что АК : КD = 3 : 1. Прямая ВК разбивает треугольник АВС на два. Найдите отношение площадей этих треугольников. (на слайде 7 рисунок 1)

Решение: Пусть АD = DC = a, KD = m, тогда АК = 3m. Пусть Р – точка пересечения прямой ВК со стороной АС. Необходимо найти отношение . Так как треугольники АВР и РВС имеют равные высоты, проведенные из вершины В, то = . По теореме Менелая для треугольника ADC и секущей РВ имеем: . Итак, = .

В треугольнике АВС, описанном около окружности, АВ = 8, ВС = 5, АС = 4. А₁ и С₁ – точки касания, принадлежащие соответственно сторонам ВС и ВА. Р – точка пересечения отрезков АА₁ и СС₁. Точка Р лежит на биссектрисе ВВ₁. Найдите АР : РА₁.

(на слайде 7 рисунок 2)

Решение: Точка касания окружности со стороной АС не совпадает с В₁, так как треугольник АВС – разносторонний. Пусть С₁В = х, тогда, используя свойство касательных, проведенных к окружности из одной точки, введем обозначения (см рисунок) 8 – х + 5 – х = 4, х = .

Значит, С₁В = ВА₁ = , А₁С = 5 — = , АС₁ = 8 — = .

В треугольнике АВА₁ прямая С₁С пересекает две его стороны и продолжение третьей стороны. По теореме Менелая .

Стороны треугольника 5, 6 и 7. Найдите отношение отрезков, на которые биссектриса большего угла этого треугольника разделена центром окружности, вписанной в треугольник. (на слайде 7).

Решение: Пусть в треугольнике АВС АВ = 5, ВС = 7, АС = 6. Угол ВАС лежит против большей стороны в треугольнике АВС, значит, угол ВАС – больший угол треугольника. Центр вписанной окружности треугольника лежит на пересечении биссектрис. Пусть О – точка пересечения биссектрис. Необходимо найти АО : ОD. Так как АD – биссектриса треугольника АВС, то , то есть BD = 5k, DС = 6k. так как BF – биссектриса треугольника АВС, то , то есть AF = 5m, FC = 7m. Прямая BF пересекает две стороны и продолжение третьей стороны треугольника ADC. По теореме Менелая .

4. Самостоятельное решение задач 9, 10, 11. – 3 учащихся.

Задача 12 (для всех оставшихся учащихся класса):

Биссектрисы ВЕ и АD треугольника АВС пересекаются в точке Q. Найдите площадь треугольника АВС, если площадь треугольника BQD = 1, 2АС = 3 АВ, 3ВС = 4 АВ. (рисунок 4 на слайде 7).

Решение: Пусть АВ = а, тогда АС = , ВС = . АD — биссектриса треугольника АВС, тогда , то есть BD = 2p, DC = 3p. ВЕ – биссектриса треугольника АВС, тогда , АЕ = 3 k, ЕС = 4k. В треугольнике ВЕС прямая АD пересекает две его стороны и продолжение третьей стороны. По теореме Менелая , , , то есть EQ = 9m, QB = 14m. Треугольники QBD и EBC имеют общий угол, значит , S_ЕВС = .

Треугольники АВС и ВЕС имеют равные высоты, проведенные из вершины В, значит, , тогда S_ABC = _.

5. Разбор задач 9, 10, 11.

Решение задач – практикум:

А. На сторонах ВС, СА, АВ равнобедренного треугольника АВС с основанием АВ взяты точки А_1, В₁, С_1, так что прямые АА₁, ВВ₁, СС₁ – конкурентные.

Докажите, что

По теореме Чевы имеем: (1 ).

По теореме синусов:, откуда СА₁ = СА .,

, откуда А₁В = АВ . , ,

откуда АВ₁ = АВ . , , откуда В₁С = ВС . , так как СА = ВС по условию. Подставив полученные равенства в равенство (1 ) получим:

.

Что и требовалось доказать.

В. На стороне АС треугольника АВС взята такая точка М, что АМ = ?АС, а на продолжении стороны ВС – такая точка N, что BN = СВ. В каком отношении точка Р – точка пересечения отрезков АВ и MN делит каждый из этих отрезков?

По теореме Менелая для треугольника АВС и секущей MN имеем:

. По условию следовательно ,

так как 0,5 . (-2) . х = 1, — 2х = — 2, х = 1.

Для треугольника MNC и секущей АВ по теореме Менелая имеем: по условию

значит, — , откуда, .

8. Самостоятельное решение задач: 1 вариант:

1. На продолжениях сторон АВ, ВС, АС треугольника АВС взяты соответственно точки С₁, А₁, В₁ так, что АВ = ВС₁, ВС = СА₁, СА = АВ₁. Найдите отношение в котором прямая АВ₁ делит сторону А₁С₁ треугольника А₁В₁С₁. (3 балла).

2. На медиане СС₁ треугольника АВС взята точка М. Прямые АМ и ВМ пересекают стороны треугольника соответственно в точках А₁ и В₁. Докажите, что прямые АВ и А₁В₁ параллельны. (3 балла).

3. Пусть на продолжении сторон АВ, ВС и АС треугольника АВС взяты соответственно точки С₁, А₁ и В_1. Докажите, что точки А₁, В_1, С₁ лежат на одной прямой тогда и только тогда, когда выполняется равенство . (4 балла).

4. Используя теорему Чевы, докажите, что высоты треугольника или их продолжения пересекаются в одной точке. (4 балла).

5. Докажите, что прямые, проходящие через вершины треугольника и точки касания вневписанных окружностей, пересекаются в одной точке (точке Нагеля). (Окружность называется вневписанной в треугольник, если она касается одной стороны этого треугольника и продолжений двух других его сторон). (5 баллов).

6. Пусть на сторонах АВ, ВС и АС треугольника АВС взяты соответственно точки С₁, А₁ и В₁ так, что прямые АА₁, ВВ₁, СС₁ пересекаются в точке О. Докажите, что выполняется равенство . (5 баллов).

7. Пусть на ребрах АВ, ВС, СD и АD тетраэдра АВСD взяты соответственно точки А₁, В₁, С₁, D_1. Докажите, что точки А₁, В₁, С₁, D₁ лежат в одной плоскости тогда и только тогда, когда выполняется равенство (5 баллов).

1. Точки А₁ и В₁ делят стороны ВС и АС треугольника АВС в отношениях 2 : 1 и 1 : 2. Прямые АА₁ и ВВ₁ пересекаются в точке О. Площадь треугольника АВС равна 1. Найдите площадь треугольника ОВС. (3 балла).

2. Отрезок МN, соединяющий середины сторон АD и ВС четырехугольника АВСD делится диагоналями на три равные части. Докажите, что АВСD – трапеция, одно из оснований АВ или СD, которое в двое больше другого. (3 балла).

3. Пусть на стороне АВ и продолжении сторон ВС и АС треугольника АВС взяты соответственно точки С₁, А₁ и В₁. Докажите, что прямые АА₁, ВВ₁, СС₁ пересекаются в одной точке или параллельны тогда и только тогда, когда выполняется равенство . (4 балла).

4. Используя теорему Чевы, докажите, что высоты треугольника или их продолжения пересекаются в одной точке. (4 балла).

5. Докажите, что прямые, проходящие через вершины треугольника и точки касания вневписанных окружностей, пересекаются в одной точке (точке Нагеля). (Окружность называется вневписанной в треугольник, если она касается одной стороны этого треугольника и продолжений двух других его сторон). (5 баллов).

6. Пусть на сторонах АВ, ВС и АС треугольника АВС взяты соответственно точки С₁, А₁, В₁ так, что прямые АА₁, ВВ₁ и СС₁ пересекаются в точке О. Докажите, что выполняется равенство . (5 баллов).

7. Пусть на ребрах АВ, ВС, СD и АD тетраэдра АВСD взяты соответственно точки А₁, В₁, С₁, D_1. Докажите, что точки А₁, В₁, С₁, D₁ лежат в одной плоскости тогда и только тогда, когда выполняется равенство (5 баллов).

9. Домашнее задание: учебник § 3, № 855, № 861, № 859.

Видео:№199. Прямая р параллельна стороне АВ треугольника ABC. Докажите, что прямые ВССкачать

Дано : А(3 ; — 1 ; 3) В(3 ; — 2 ; 2) С(2 ; 2 ; 3) Д(1 ; 2 ; 2) Найти угол между прямыми АВ и СД?

Математика | 10 — 11 классы

Дано : А(3 ; — 1 ; 3) В(3 ; — 2 ; 2) С(2 ; 2 ; 3) Д(1 ; 2 ; 2) Найти угол между прямыми АВ и СД.

Решим через скалярное произведение векторов.

$displaystyle A(3;-1;3),; B(3;-2;2)\ vec =(3-3;-2-(-1);2-3)=(0;-1;-1)$$displaystyle C(2;2;3),; D(1;2;2)\ vec =(1-2;2-2;2-3)=(-1;0;-1)$Вычислим скалярное произведение : $displaystyle vec cdot vec =0cdot (-1)+(-1)cdot 0+(-1)cdot (-1)=\ =0+0+1=1$При этом верно и другое : $displaystyle vec cdot vec =|vec |cdot |vec |cdot cos$, где α — угол между векторами.

$displaystyle |vec |=sqrt =\ =sqrt =sqrt2$$displaystyle |vec |=sqrt =\ =sqrt =sqrt2$Получаем : $displaystyle cos =frac <veccdot vec > <|vec|cdot |vec |> =frac1 =frac12$$displaystyle alpha =arccos =60^$Угол между прямыми не превышает 90° (между векторами не превышает 180°), 60° &lt ; 90°.

Искомый угол равен 60°.

Видео:№26. Сторона АС треугольника ABC параллельна плоскости α, а стороныСкачать

Угол между высотой прямоугольного треугольника, проведенной из вершины прямого угла, биссектрисой прямого угла равен 12градусов?

Угол между высотой прямоугольного треугольника, проведенной из вершины прямого угла, биссектрисой прямого угла равен 12градусов.

Найти острые углы данного прямоугольного треугольника.

Видео:ОГЭ 23 КАК РЕШИТЬ ЗАДАЧУ НА ПОДОБНЫЕ ТРЕУГОЛЬНИКИСкачать

В треугольнике АВС угол В прямой?

В треугольнике АВС угол В прямой.

Угол А на 56 градусов больше чем угол С.

Найти углы треугольника.

Видео:№212. Прямые, содержащие высоты АА1 и ВВ1 треугольника АВС, пересекаются в точке Н, угол В - тупой,Скачать

Дано : угол COB = 60 градусов?

Дано : угол COB = 60 градусов.

Видео:Задание 3 ЕГЭ по математике. Урок 41Скачать

Помогите найти угол между прямой и плоскостью?

Помогите найти угол между прямой и плоскостью.

Видео:№31. Плоскость α параллельна стороне ВС треугольника ABC и проходит черезСкачать

Параллельные прямые а в пересечены прямой с, угол 1 = 22 градусов найти угол2?

Параллельные прямые а в пересечены прямой с, угол 1 = 22 градусов найти угол2.

Видео:Геометрия Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точкахСкачать

Помогите прошу?

Дано : a и b прямые С и К секущие угол 1 = углу 2 = 35 градусов угол 3 на 50 градусов меньше угла 4 найти : угол 3 и угол 4.

Видео:№196. Дан треугольник ABC. Сколько прямых, параллельных стороне АВ, можно провестиСкачать

Дан треугольник ABC, угол А — прямой?

Дан треугольник ABC, угол А — прямой.

Высота AH , угол С равен 45 градусам.

Найти длину стороны AC.

Видео:ОГЭ Р-2 номер 16Скачать

Построй угол больше данного угла но меньше прямого угла?

Построй угол больше данного угла но меньше прямого угла.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

В прямоугольном треугольнике угол с — прямой угол а — 48 градусов найти угол b?

В прямоугольном треугольнике угол с — прямой угол а — 48 градусов найти угол b.

Видео:№52. Две стороны треугольника параллельны плоскости α. Докажите, что и третья сторонаСкачать

Как найти площадь треугольника в котором есть прямой угол?

Как найти площадь треугольника в котором есть прямой угол.

Видео:№65. Параллельные отрезки А1А2, В1В2 и С1С2 заключены между параллельными плоскостями α и βСкачать

Дан угол ABC?

Угол ABC — прямой.

Нужно найти угол KBC, если угол ABK состовляет 0, 5 — угла ABC.

На этой странице находится вопрос Дано : А(3 ; — 1 ; 3) В(3 ; — 2 ; 2) С(2 ; 2 ; 3) Д(1 ; 2 ; 2) Найти угол между прямыми АВ и СД?. Здесь же – ответы на него, и похожие вопросы в категории Математика, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 10 — 11 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.

Сколько минут лентяй проспит через 2 дня.

1. > 2. Ну вот какие знаки в первом где . Там > ну а дальше всё написано у меня.

1) 26 — 5 = 21 (штук) — было больше ноутбуков чем игровых приставок. 2) 33600 : 21 = 1600 (руб. ) — за одну приставку или ноутбук. 3) 1600 x 26 = 41600 (руб. ) — получили за ноутбуки. 4) 1600 x 5 = 8000 (руб. ) — получили за приставки. Ответ .

1) 192 а = 48 2)240 b = 4 3)576 с = 192 4)640 d = 160 Ответь пожалуйста как лучший.

1 / 224 или просто 224.

64000 : 1000 = 64 3000 + 400 + 50 + 9 = 3459 5000 + 60 + 2 = 5062 9000 + 5 = 9005 7800•10 = 78000 400376 — 400000 — 70 = 306 543605 — 500000 — 600 = 43005 43879 — 43000 — 800 = 79.

Вот рисунком Заранее прошу лайк.

5 км + 280 м = 5280 м В 5 км = 5000 м = > 5280 м — 5000 м = 280 м.

(k — c) * (k + c) — (k + c) ^ 2 = k ^ 2 + kc — kc — c ^ 2 — k ^ 2 — 2kc + c ^ 2 = 2kc, т. К мы взаимоуничтожаем все переменные кроме 2kc.

(k — c)(k + c) — (k + c)² = 1 способ. = (k² — c² ) — (k² + 2kc + c² ) = = k² — c² — k² — 2kc — c² = = — 2c² — 2kc = можно вынести общий множитель : = ( — 2с)(с + k) 2 способ. = (k + c)(k — c) — (k + c)(k + c) = = (k + c) * (k — c — (k + c)) = = (k ..

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

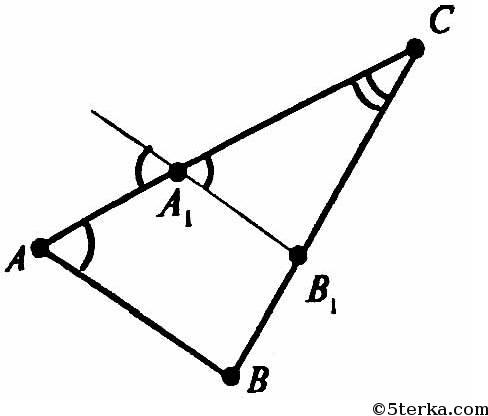
13. Дан треугольник АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС этого треугольника в точке А1, а сторону ВС — в точке В1.

Найдите длину отрезка А₁В₁, если:

1) АВ = 15 см, АА₁ : АС = 2 : 3;

2) АВ = 8 см, АА₁ : А₁С = 5 : 3;

3) В₁С = 10 см, АВ : ВС = 4 : 5;

Так как AB параллельна плоскости, то AB || A₁B₁, так как A₁B₁ лежит в плоскости. А, значит, ΔABC

Решебник по геометрии за 10 класс (А.В. Погорелов, 2001 год),
задача №13
к главе «§ 16. Параллельность прямых и плоскостей».

🔍 Видео

№126. Прямая MB перпендикулярна к сторонам АВ и ВС треугольника ABC. Определите вид треугольникаСкачать

Все типы 15 задания ОГЭ 2022 математика | Геометрия на ОГЭСкачать

№21. Треугольники ABC и ABD не лежат в одной плоскости. Докажите,Скачать

№473. Через вершину С треугольника ABC проведена прямая m, параллельная стороне АВ. Докажите,Скачать

Задача 1.1. Прямая и плоскость. Построить комплексный чертеж треугольника АВС и прямой МN.Скачать

Параллельность прямой к плоскостиСкачать

Параллельность прямых. 10 класс.Скачать