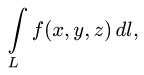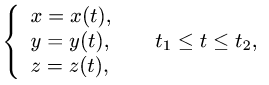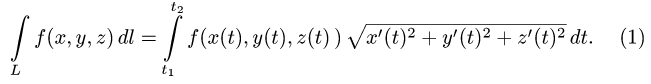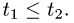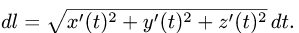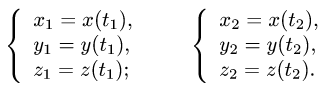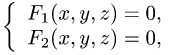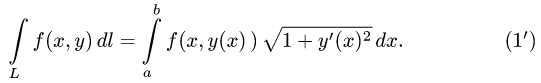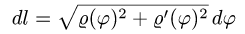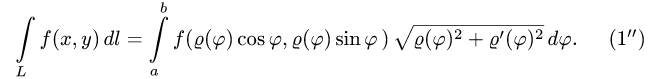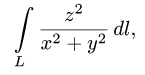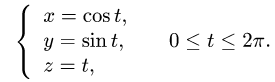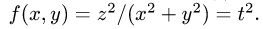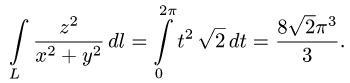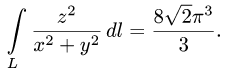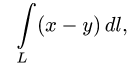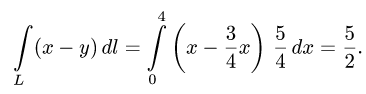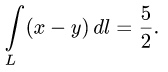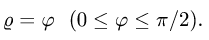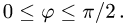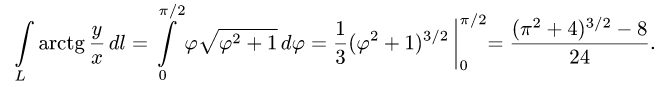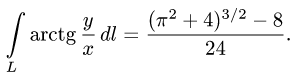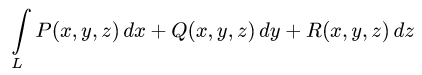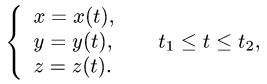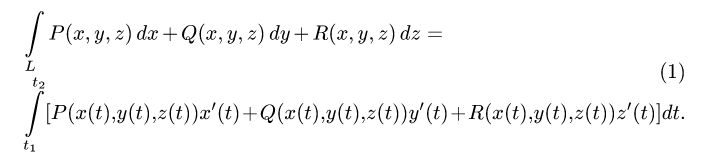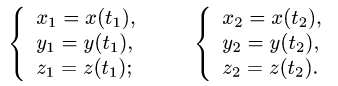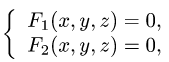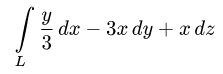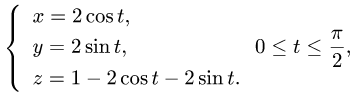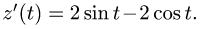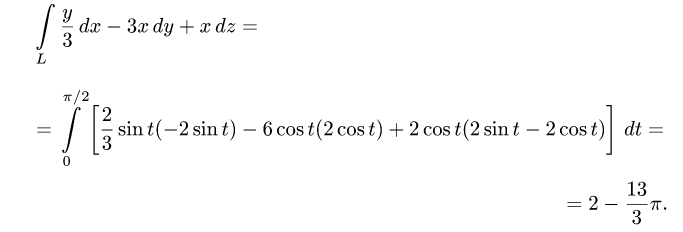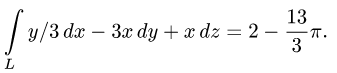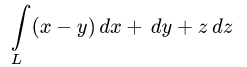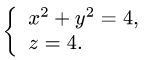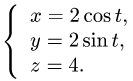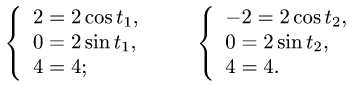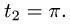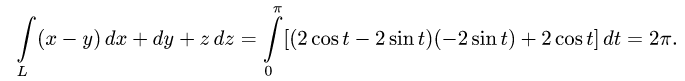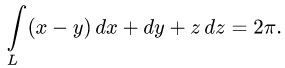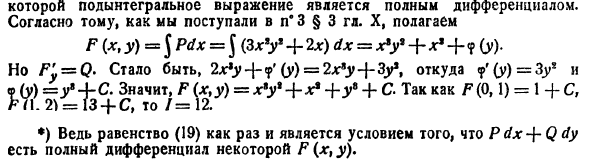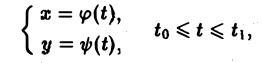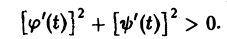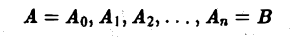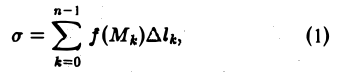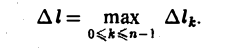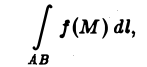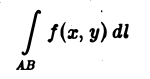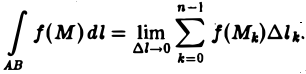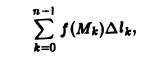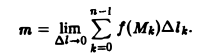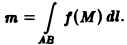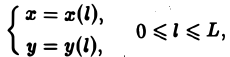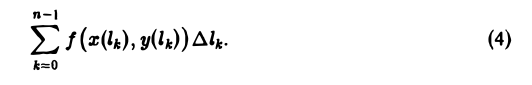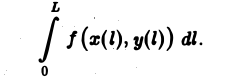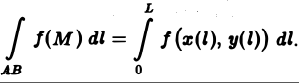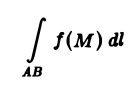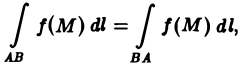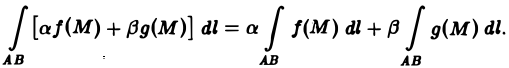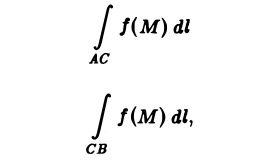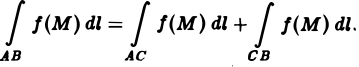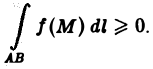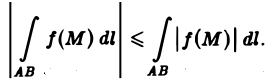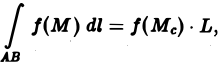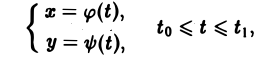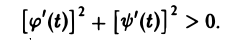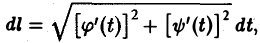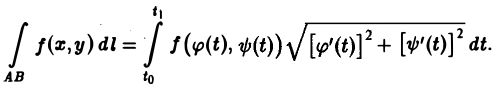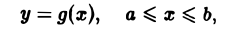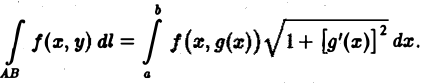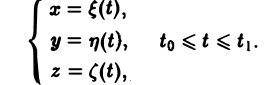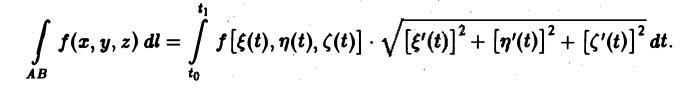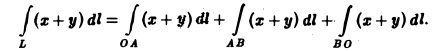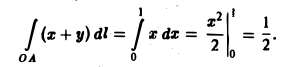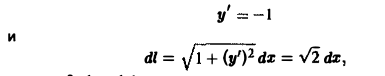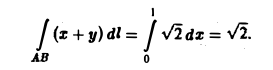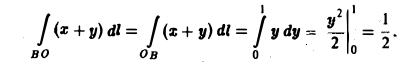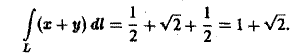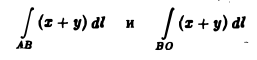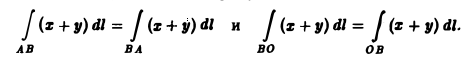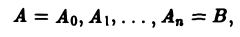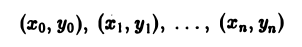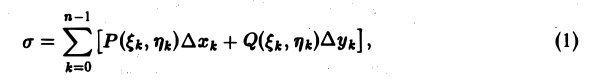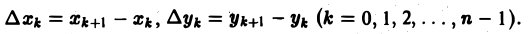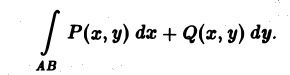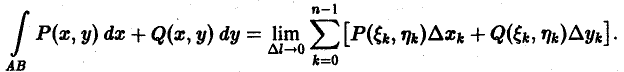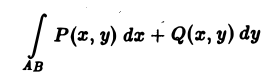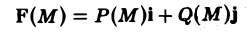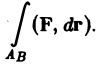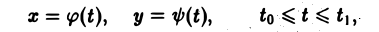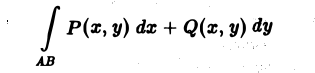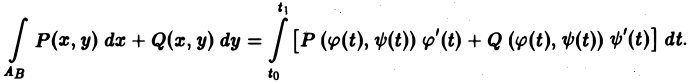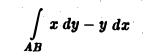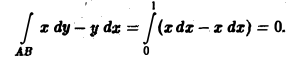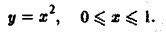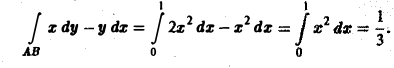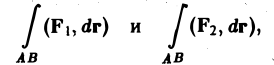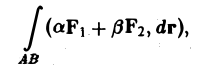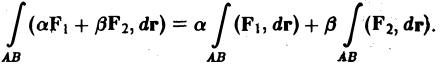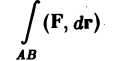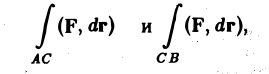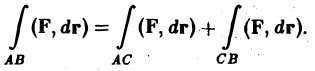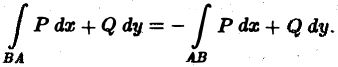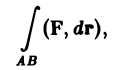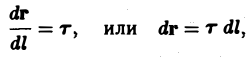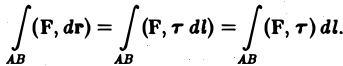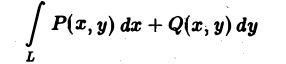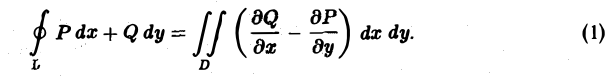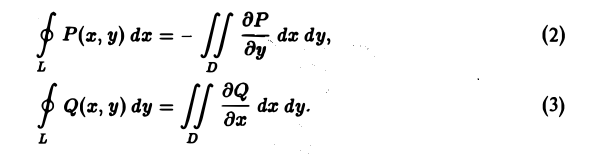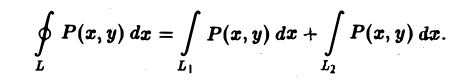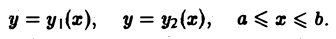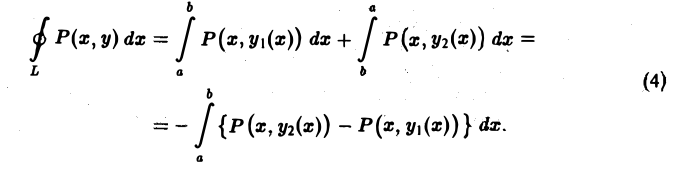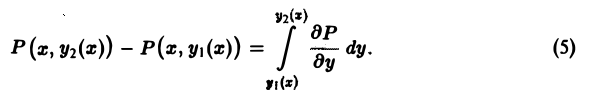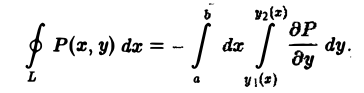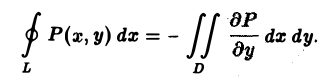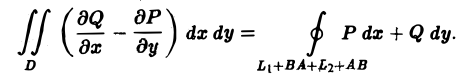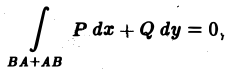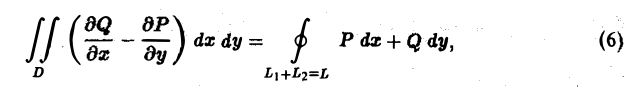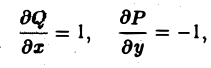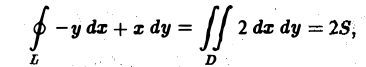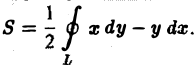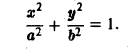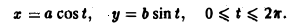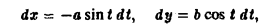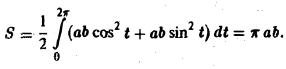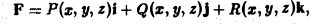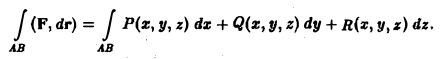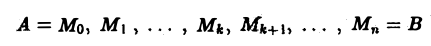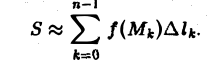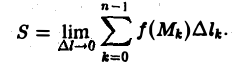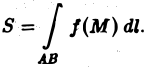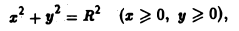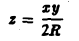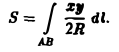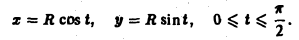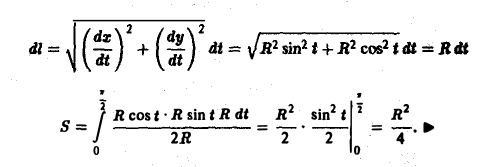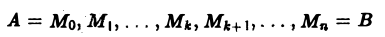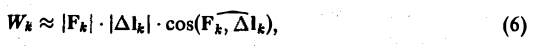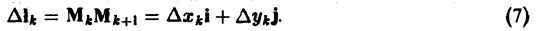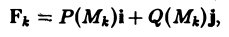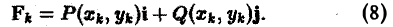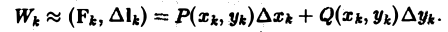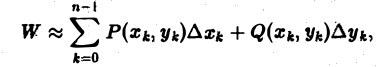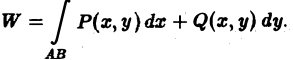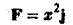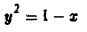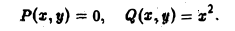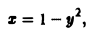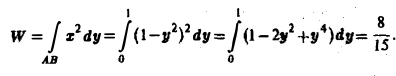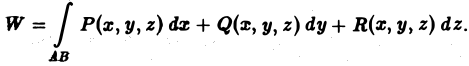Вычислить криволинейный интеграл по окружности

В этом разделе вы найдете подробные решения криволинейных интегралов первого и второго рода (непосредственное вычисление, по разным путям, по формуле Грина), а также применение к вычислению моментов инерции, массы, работы, силы притяжения и т.п.

Видео:Криволинейный интеграл II рода вдоль плоской кривойСкачать

Криволинейные интегралы 1-го рода: примеры решений

Задача 1. Вычислить криволинейный интеграл первого рода по указанной кривой $L$:

Задача 2. Вычислить криволинейный интеграл I рода $int_L y^2 dl$, $L$ — арка циклоиды $x=(t-sin t)/2$, $y=(1-cos t)/2$, $0 le t le pi$.

Задача 3. Вычислить криволинейный интеграл $int_L y^2 dl$, где $L$ – дуга параболы $y^2=2x$ от точки $(0;0)$ до точки $(1;sqrt)$.

Если вам нужна помощь в нахождении интегралов, выполнении домашней работы, будем рады принять ваш заказ на решение. Стоимость от 100 рублей, срок от нескольких часов.

Видео:Математический анализ, 47 урок, Криволинейные интегралы первого родаСкачать

Криволинейные интегралы 2-го рода: примеры решений

Задача 4. Вычислить криволинейный интеграл второго рода, взятый вдоль ориентированной кривой $L$: $int_L x^2 dy -xydx$, где $L$ — часть кривой $x^4-y^4=6x^2y$ от точки $A=(-4sqrt;4)$ до точки $B=(0;0)$

Задача 5. Вычислить интеграл $$int_L z^2x dx +(z+x+y)dy +y^2zdz,$$ где $L$ — кривая $a^2+y^2=ax, x^+y^2=z^2$ положительно ориентированная на внешней стороне цилиндра.

Задача 6. Вычислить криволинейный интеграл $int_ (y^2+x)dx+2x/y dy$ вдоль кривой $y=e^x$ от точки $A(0;1)$ до точки $B(1;e)$.

Задача 7. Проверить, что криволинейный интеграл не зависит от пути интегрирования и найти его значение.

Задача 8. Проверить криволинейный интеграл, который не зависит от пути интегрирования, и найти его значение (двумя способами – непосредственно и с помощью потенциала).

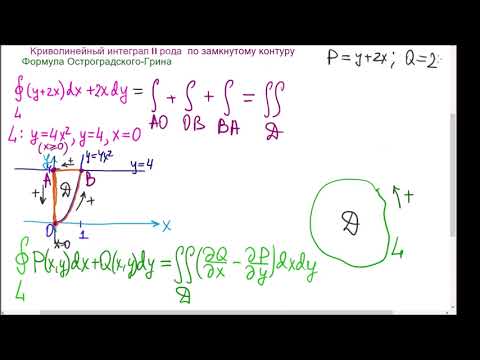
Задача 9. Вычислить криволинейный интеграл по замкнутому контуру в положительном направлении, используя формулу Грина

$$int_l (x-y^2)dy + (x^3+3y)dx, quad l: x=y, y=x^2.$$

Трудности с задачами? МатБюро поможет с интегралами.

Видео:Математический анализ, 48 урок, Криволинейные интегралы второго родаСкачать

Моменты инерции: примеры решений

Задача 10. Найти моменты инерции относительно осей однородных дуг $L$ плотности $rho$.

Задача 11. Вычислить момент инерции верхней половины окружности $x^2+y^2=a^2$ относительно оси $Oy$, если плотность $delta=1$.

Видео:Формула ГринаСкачать

Другие задания: примеры решений

Задача 12. Найти координаты силы притяжения дугой астроиды $x=a cos^3 t$, $y=a sin^3 t$, $0 le t le pi/2$ единичной массы, помещенной в начале координат, если плотность астроиды в каждой ее точке равна кубу расстояния этой точки от начала координат.

Задача 13. Вычислить работу силы $F(z,-x,y)$ вдоль дуги винтовой линии $z=2cos t$, $y=3sin t$, $z=4t$, $0 le t le 2pi$.

Задача 14. Доказать, что данное выражение $P(x,y)dx+Q(x,y)dy$ является полным дифференциалом функции $Ф(x,y)$ и найти ее с помощью криволинейного интеграла.

Задача 15. Вычислить работу силы $overline$ при перемещении точки приложения силы вдоль заданной кривой $L$ от точки $B$ до точки $C$, если значения параметра $t$ в точках $B$ и $C$ заданы.

$$ overline=-x overline+2y^2overline, quad x=2cos t, y=sint, quad t_B=0, t_C=pi/6. $$

Задача 16. Вычислить массу кривой $y=x^2/2$, где $xin (sqrt, 2sqrt)$, если линейная плотность задана функцией $f(x,y)=6y/x$.

Видео:Криволинейный интеграл по длине дуги ➜ Криволинейный интеграл 1-го родаСкачать

Вычисление криволинейных интегралов: теория и примеры

Видео:Криволинейный интеграл первого родаСкачать

Понятие криволинейного интеграла

Криволинейные интегралы — обобщение понятия определённого интеграла на случай, когда областью интегрирования является отрезок некоторой кривой, лежащий в плоскости. Общая запись криволинейного интеграла следующая:

где f(x, y) — функция двух переменных, а L — кривая, по отрезку AB которой происходит интегрирование. Если подынтегральная функция равна единице, то криволинейный интеграл равен длине дуги AB.

Как всегда в интегральном исчислении, криволинейный интеграл понимается как предел интегральных сумм каких-то очень маленьких частей чего-то очень большого. Что же суммируется в случае криволинейных интегралов?

Пусть на плоскости расположен отрезок AB некоторой кривой L, а функция двух переменных f(x, y) определена в точках кривой L. Пусть мы выполняем с этим отрезком кривой следующий алгоритм.

1. Разделить кривую AB на части точками (рисунки ниже).
2. В каждой части свободно выбрать точку M.
3. Найти значение функции в выбранных точках.
4. Значения функции умножить на
   • длины частей в случае криволинейного интеграла первого рода;
   • проекции частей на ось координат в случае криволинейного интеграла второго рода.
5. Найти сумму всех произведений.
6. Найти предел найденной интегральной суммы при условии, что длина самой длинной части кривой стремится к нулю.

Если упомянутый предел существует, то этот предел интегральной суммы и называется криволинейным интегралом от функции f(x, y) по кривой AB.

Случай криволинейного интеграла
первого рода

Случай криволинейного интеграла
второго рода

Введём следующие ообозначения.

M i (ζ i ; η i ) — выбранная на каждом участке точка с координатами.

f i (ζ i ; η i ) — значение функции f(x, y) в выбранной точке.

Δs i — длина части отрезка кривой (в случае криволинейного интеграла первого рода).

Δx i — проекция части отрезка кривой на ось Ox (в случае криволинейного интеграла второго рода).

d = maxΔs i — длина самой длинной части отрезка кривой.

Криволинейные интегралы первого рода

Исходя из вышеизложенного о пределе интегральных сумм, криволинейный интеграл первого рода записывается так:

.

Криволинейный интеграл первого рода обладает всеми свойствами, которыми обладает определённый интеграл. Однако есть одно важное различие. У определённого интеграла при перемене местами пределов интегрирования знак меняется на противоположный:

.

В случае же криволинейного интеграла первого рода не имеет значения, какую из точек кривой AB (A или B) считать началом отрезка, а какую концом, то есть

.

Криволинейные интегралы второго рода

Исходя из изложенного о пределе интегральных сумм, криволинейный интеграл второго рода записывается так:

.

В случае криволинейного интеграла второго рода при перемене местами начала и конца отрезка кривой знак интеграла меняется:

.

При составлении интегральной суммы криволинейного интеграла второго рода значения функции f i (ζ i ; η i ) можно умножать также на проекции частей отрезка кривой на ось Oy. Тогда получим интеграл

.

На практике обычно используется объединение криволинейных интегралов второго рода, то есть две функции f = P(x, y) и f = Q(x, y) и интегралы

,

а сумма этих интегралов

называется общим криволинейным интегралом второго рода.

Видео:Криволинейный интеграл 1 родаСкачать

Вычисление криволинейных интегралов первого рода

Вычисление криволинейных интегралов первого рода сводится к вычислению определённых интегралов. Рассмотрим два случая.

Кривая дана в декартовых прямоугольных координатах

Пусть на плоскости задана кривая y = y(x) и отрезку кривой AB соответствует изменение переменной x от a до b. Тогда в точках кривой подынтегральная функция f(x, y) = f(x, y(x)) («игрек» должен быть выражен через «икс»), а дифференциал дуги и криволинейный интеграл можно вычислить по формуле

.

Если интеграл проще интегрировать по y, то из уравнения кривой нужно выразить x = x(y) («икс» через «игрек»), где и интеграл вычисляем по формуле

.

Пример 1. Вычислить криволинейный интеграл

,

где AB — отрезок прямой между точками A(1; −1) и B(2; 1) .

Решение. Составим уравнение прямой AB , используя формулу (уравнение прямой, проходящей через две данные точки A(x 1 ; y 1 ) и B(x 2 ; y 2 ) ):

.

Из уравнения прямой выразим y через x :

.

Тогда и теперь можем вычислять интеграл, так как у нас остались одни «иксы»:

Кривая дана в параметрической форме

Пусть в пространстве задана кривая

Тогда в точках кривой функцию нужно выразить через параметр t () а дифференциал дуги , поэтому криволинейный интеграл можно вычислить по формуле

Аналогично, если на плоскости задана кривая

,

то криволинейный интеграл вычисляется по формуле

.

Пример 2. Вычислить криволинейный интеграл

,

где L — часть линии окружности

,

находящаяся в первом октанте.

Решение. Данная кривая — четверть линии окружности, расположенная в плоскости z = 3 . Она соответствует значениям параметра . Так как

,

то дифференциал дуги

Подынтегральную функцию выразим через параметр t :

.

Теперь, когда у нас всё выражено через параметр t , можем свести вычисление данного криволинейного интеграла к определённому интегралу:

Видео:Формула ГринаСкачать

Вычисление криволинейных интегралов второго рода

Так же, как и в случае криволинейных интегралов первого рода, вычисление интегралов второго рода сводится к вычислению определённых интегралов.

Кривая дана в декартовых прямоугольных координатах

Пусть дана кривая на плоскости уравнением функции «игрек», выраженной через «икс»: y = y(x) и дуге кривой AB соответствует изменение x от a до b . Тогда в подынтегральную функцию подставим выражение «игрека» через «икс» и определим дифференциал этого выражения «игрека» по «иксу»: . Теперь, когда всё выражено через «икс», криволинейный интеграл второго рода вычисляется как определённый интеграл:

Аналогично вычисляется криволинейный интеграл второго рода, когда кривая дана уравнением функции «икс», выраженной через «игрек»: x = x(y) , . В этом случае формула для вычисления интеграла следующая:

Пример 3. Вычислить криволинейный интеграл

, если

а) Вычислим криволинейный интеграл по отрезку прямой (на рисунке — синяя). Напишем уравнение прямой и выразим «игрек» через «икс»:

.

Получаем dy = dx . Решаем данный криволинейный интеграл:

б) если L — дуга параболы y = x² , получим dy = 2xdx . Вычисляем интеграл:

В только что решённом примере получили в двух случаях один и тот же результат. И это не совпадение, а результат закономерности, так как данный интеграл удовлетворяет условиям следующей теоремы.

Теорема. Если функции P(x,y) , Q(x,y) и их частные производные , — непрерывные в области D функции и в точках этой области частные производные равны, то криволинейный интеграл не зависит от пути интегрирования по линии L , находящейся в области D .

Кривая дана в параметрической форме

Пусть в пространстве дана кривая

.

,

а в подынтегральные функции подставим

—

выражения этих функций через параметр t . Получаем формулу для вычисления криволинейного интеграла:

Пример 4. Вычислить криволинейный интеграл

,

если L — часть эллипса

отвечающая условию y ≥ 0 .

Решение. Данная кривая — часть эллипса, находящаяся в плоскости z = 2 . Она соответствует значению параметра .

,

можем представить криволинейный интеграл в виде определённого интеграла и вычислить его:

Если дан криволинейный интеграл и L — замкнутая линия, то такой интеграл называется интегралом по замкнутому контуру и его проще вычислить по формуле Грина.

Видео:Найдите массу дуги окружности ➜ Физический смысл криволинейного интеграла 1-го рода (по длине дуги)Скачать

Больше примеров вычисления криволинейных интегралов

Пример 5. Вычислить криволинейный интеграл

,

где L — отрезок прямой между точками её пересечения с осями координат.

Решение. Определим точки пересечения прямой с осями координат. Подставив в уравнение прямой y = 0 , получим , . Подставив x = 0 , получим , . Таким образом, точка пересечения с осью Ox — A(2; 0) , с осью Oy — B(0; −3) .

Из уравнения прямой выразим y :

.

, .

Теперь можем представить криволинейный интеграл в виде определённого интеграла и начать вычислять его:

В подынтегральном выражении выделяем множитель , выносим его за знак интеграла. В получившемся после этого подынтегральном выражении применяем подведение под знак дифференциала и окончательно получаем:

Пример 6. Вычислить криволинейный интеграл

,

где L — дуга параболы между точками О(0; 0) и B(2; 2) .

Решение. Так как , то .

Теперь можем представить криволинейный интеграл в виде определённого интеграла и вычислить его:

Пример 7. Вычислить криволинейный интеграл

,

где L — дуга астроиды

в первом квадранте.

Решение. В первом квадранте . Определим дифференциал дуги:

Представляем криволинейный интеграл в виде определённого интеграла и вычисляем его:

Пример 8. Вычислить криволинейный интеграл

,

где L — первая арка циклоиды

Решение. Циклоида образует первую арку при изменении параметра t от 0 до 2π . Определим дифференциал дуги:

.

Подставим в криволинейный интеграл dl и y , выраженные через параметр t и получаем:

Пример 9. Вычислить криволинейный интеграл

,

где L — отрезок прямой от точки A(1; 1) до точки B(3; 5) .

Решение. Составим уравнение прямой AB :

.

Из полученного уравнения прямой выразим «игрек»:

Поэтому и теперь можем вычислить данный криволинейный интеграл:

Пример 10. Вычислить криволинейный интеграл

,

где L — первая арка циклоиды

Решение. Из уравнений кривой следует

.

Так как циклоида образует первую арку при изменении параметра t от 0 до 2π , то получаем соответствующие пределы интегрирования. Решаем данный криволинейный интеграл:

.

Уравнением кривой M 0 M 1 является y = 1 , тогда dy = 0 , на кривой M 1 M x — константа, значит, dx = 0 . Продолжаем и завершаем решение:

Вычисление длины дуги кривой

Если подынтегральная функция равна единице, то криволинейный интеграл первого рода равен длине дуги кривой L:

.

Пример 12. Вычислить длину дуги кривой

,

где .

Решение. Составляем криволинейный интеграл первого рода:

.

Определим производную «игрека»:

.

Продолжаем и завершаем решение:

Вычисление площади участка плоскости

Если границей участка D плоскости является кривая L, то площадь участка D можно вычислить в виде криволинейного интеграла второго рода

.

Пример 13. Вычислить площадь участка плоскости, ограниченного эллипсом

.

Решение. Площадь участка плоскости можно вычислить как криволинейный интеграл второго рода

,

где L — замкнутая линия, ограничивающая участок. Так как

.

Вычисление площади цилиндрической поверхности

Пусть на плоскости xOy дана гладка кривая L, в точках которой определена непрерывная функция двух переменных . Построим цилиндрическую поверхность, образующая которой параллельна оси Oz, и которая заключена между кривой L и поверхностью . Площадь этой цилиндрической поверхности можно вычислить по формуле

.

Вычисление массы материальной кривой

Если L — материальная кривая с плотностью , то массу материальной кривой можно вычислить по формуле

Определение статических моментов материальной кривой

Статические моменты материальной кривой с плотностью относительно осям координат вычисляются по формулам

,

.

Вычисление моментов инерции материальной кривой

Моменты инерции материальной кривой с плотностью относительно осей координат и начала системы координат можно вычислить по формулам

,

,

.

Вычисление координат центра тяжести материальной кривой

Координаты центра тяжести материальной кривой с плотностью можно определить по формулам

,

.

Вычисление работы силы

Если под воздействием переменной силы материальная точка перемещается из точки M в точку N по кривой L=MN, то приложенную работу можно вычислить по формуле

.

Пример 14. В каждой точке плоскости действует сила . Вычислить работу, совершаемую силой при перемещении единицы массы по дуге параболы из точки O(0;0) в точку А(4;2) .

Решение. Работу силы вычислим как криволинейный интеграл второго рода

.

Используя уравнение параболы, производим замену переменной

Видео:Формула Остроградского - ГринаСкачать

Криволинейные интегралы в математике с примерами решения и образцами выполнения

При изучении темы «Криволинейные интегралы» вы познакомитесь с понятиями криволинейных интегралов первого рода (по длине дуги) и второго рода (по координатам) от функций двух и трех переменных и научитесь вычислять их вдоль различных плоских и пространственных кривых, заданных параметрически, в декартовых и в полярных координатах, приводя криволинейные интегралы к определенным.

Видео:Криволинейный интеграл 2 родаСкачать

Криволинейные интегралы первого рода

Постановка задачи. Вычислить криволинейный интеграл

где L — часть гладкой кривой, заданной параметрически

и dl — дифференциал длины дуги.

План решения. Криволинейный интеграл первого рода по кривой L определяется формулой

Подчеркнем, что криволинейный интеграл первого рода не зависит
от направления обхода кривой и всегда

1.Вычисляем 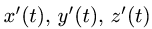и

2.Вычисляем криволинейный интеграл по формуле (1) и записываем ответ.

Замечание:

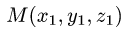
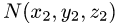
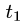
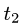
Если граничные точки кривой L и
заданы в декартовых координатах, то и определяем, решая системы уравнений

Замечание:

Если кривая задана как линия пересечения двух
поверхностей:

то ее необходимо параметризовать.

Замечание:

Если плоская кривая задана уравнением у = у(х)
то дифференциал длины дуги равен и формула (1) имеет вид

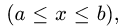
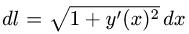
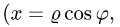
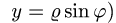
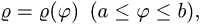
Если плоская кривая задана в полярных координатах уравнением то дифференциал длины дуги равен

и формула (1) имеет вид

Пример:

Вычислить криволинейный интеграл

где L — первый виток винтовой линии

Решение:

1.Вычисляем: x'(t) = — sin t, y'(t) = cos t, z'(t) = 1, 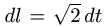и

2.Подставляем эти результаты в формулу (1) и вычисляем определенный интеграл:

Ответ.

Пример:

Вычислить криволинейный интеграл

где L — отрезок прямой от точки А(0, 0) до точки В(4, 3).

Решение:

1.В данном случае уравнение прямой есть 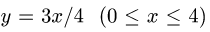и, следовательно, и

2.Подставляем эти результаты в формулу (1) и вычисляем определенный интеграл:

Ответ.

Пример:

Вычислить криволинейный интеграл

где L — часть спирали Архимеда

Решение:

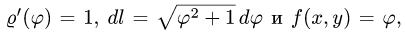
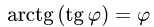
1.Вычисляем: так как при

2.Подставляем эти результаты в формулу (1″) и вычисляем определенный интеграл:

Ответ.

Видео:Криволинейные интегралы. Примеры.Скачать

Криволинейные интегралы второго рода

Постановка задачи. Вычислить криволинейный интеграл

где L — часть гладкой кривой, заданной параметрически

План решения. Криволинейный интеграл второго рода по кривой L определяется формулой

1.Вычисляем x'(t), y'(t) и z'(t).

2.Вычисляем криволинейный интеграл по формуле (1) и записываем ответ.

Замечание:

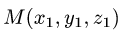
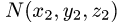
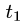
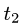
Если граничные точки кривой L и
заданы в декартовых координатах, то и определяем, решая системы уравнений

Замечание:

Если кривая задана как линия пересечения двух
поверхностей:

то ее необходимо параметризовать.

Пример:

Вычислить криволинейный интеграл

по части кривой L, заданной параметрически

Решение:

1.Вычисляем: x'(t) = — 2sin t, y'(t) = 2cos t и

2.Вычисляем криволинейный интеграл по формуле (1):

Ответ.

Пример:

Вычислить криволинейный интеграл

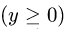
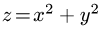
от точки М(2,0, 4) до точки N(—2,0,4) по кривой L, образованной пересечением параболоида и плоскости z = 4,

Решение:

В сечении получается окружность

Поэтому параметрические уравнения кривой L имеют вид

1.Вычисляем: х'(t) = -2sin t, у'(t) = 2cos t и z'(t) = 0.

Определяем 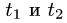из условий

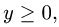
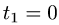
Учитывая, что получаем и

2.Вычисляем криволинейный интеграл по формуле (1):

Ответ.

Видео:Интеграл по замкнутому контуру.Без формулы ГринаСкачать

Дополнение к криволинейному интегралу

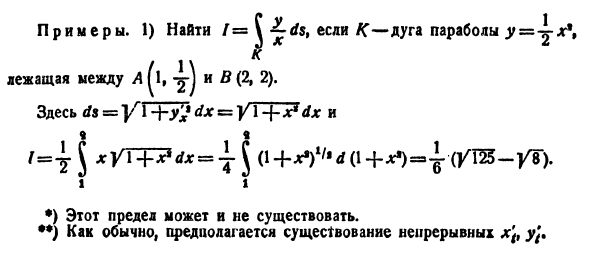
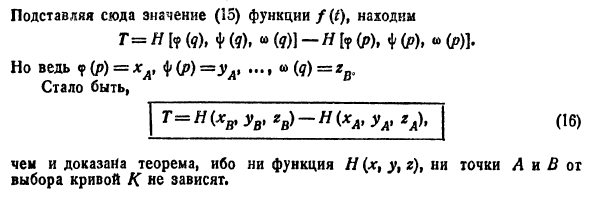
Видео:Криволинейные интегралы 1 и 2 рода – что такое и в чём разница? | Лекция 27 | МатанализСкачать

Решение криволинейных интегралов

Кривая АВ, заданная параметрическими уравнениями

называется гладкой, если функции φ(t) и ψ(t) имеют на отрезке [tо, t1] непрерывные производные φ'(t) и ψ'(t), причем

Если в конечном числе точек отрезка [tо, t1] эти производные не существуют или одновременно обращаются в нуль, то кривая называется кусочно-гладкой.

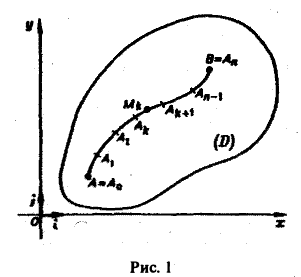
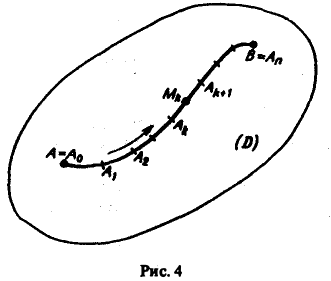
Пусть АВ — плоская кривая, гладкая или кусочно-гладкая. Пусть f(M) — функция, заданная на кривой АВ или в некоторой области D, содержащей эту кривую. Рассмотрим разбиение кривой АВ на части точками

Выберем на каждой из дуг AkAk+1 произвольную точку Мk и составим сумму

где ∆lk — длина дуги AkAk+1 и назовем ее интегральной суммой для функции f(M) по длине дуги кривой. Пусть ∆l — наибольшая из длин частичных дуг, т.е.

Определение:

Если при ∆l —► 0 интегральная сумма (1) имеет конечный предел, не зависящий ни от способа разбиения кривой АВ на части, ни от выбора точек на каждой из дуг разбиения, то этот предел называется криволинейным интегралом 1 -го рода от функции f(M) по кривой АВ (интеграл по длине дуги кривой) и обозначается символом

(точка М(х, у) лежит на кривой АВ).
В этом случае функция f(M) называется интегрируемой вдоль кривой АВ, кривая АВ называется контуром интегрирования, А — начальной, В — конечной точками интегрирования. Таким образом, по определению,
(2)

Пример:

Пусть вдоль некоторой гладкой кривой L распределена масса с переменной линейной плотностью f(M). Найти массу т кривой L.

Разобьем кривую L на п произвольных частей MkMk+1 (k = 0,1,… , n —1) и вычислим приближенно массу каждой части, предполагая, что на каждой из частей MkMk+1 плотность постоянна и равна плотности в какой-нибудь из ее точек, например, в крайней левой точке f(Mk). Тогда сумма

где ∆lk — длина k-ой части, будет приближенным значением массы т. Ясно, что погрешность будет тем меньше, чем мельче разбиение кривой L. В пределе при ∆l → 0 (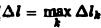) получим точное значение массы всей кривой L, т.е.

Но предел справа есть криволинейный интеграл 1-го рода. Значит,

Существование криволинейного интеграла 1-го рода

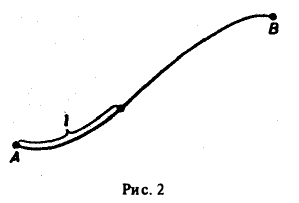
Примем на кривой АВ за параметр длину дуги I, отсчитываемую от начальной точки А (рис. 2). Тогда кривую АВ можно описать уравнениями
(3)

где L — длина кривой АВ.

Уравнения (3) называются натуральными уравнениями кривой АВ. При переходе к натуральным уравнениям функция f(x, у), заданная на кривой АВ, сведется к функции переменной l: f(x(l), y(l). Обозначив через lk (k = 0, 1,…, п — 1) значение параметра l, отвечающее точке Мk, перепишем интегральную сумму (1) в виде

Это — интегральная сумма, отвечающая определенному интегралу

Поскольку интегральные суммы (1) и (4) равны между собой, то равны и отвечающие им интегралы. Таким образом,
(5)

Теорема:

Если функция f(M) непрерывна вдоль гладкой кривой АВ, то существует криволинейный интеграл

(поскольку при этих условиях существует определенный интеграл, стоящий в равенстве (5) справа ).

Свойства криволинейных интегралов 1-го рода

1, Из вида интегральной суммы (1) следует, что

т.е. величина криволинейного интеграла 1-го рода не зависит от направления интегрирования.

2. Линейность. Если для каждой из функций f(M) и д(М) существует криволинейный интеграл по кривой АВ, то для функции af(M) + βg<М), где а и β — любые постоянные, также существует криволинейный интеграл по кривой АВ, причем

3. Аддитивность. Если кривая АВ состоит из двух кусков АС и С В и для функции f(М) существует криволинейный интеграл по AВ, то существуют интегралы

4. Если f(M) ≥ 0 на кривой AB, то

5. Если функция f(M) интегрируема на кривой АВ, то функция |f(М)| также интегрируема на АВ, и при этом

6. Формула среднего значения. Если функция f(M) непрерывна вдоль кривой АВ, то на этой кривой найдется точка Мс такая, что

где L — длина кривой AB.

Вычисление криволинейного интеграла 1-го рода

Пусть кривая АВ задана параметрическими уравнениями

причем точке А соответствует значение t = t0, а точке В — значение t = t1. Будем предполагать, что функции φ(t) и ψ(t) непрерывны на [to, t1] вместе со своими производными φ'(t) и ψ'(t) и выполнено неравенство

Тогда дифференциал дуги кривой вычисляется по формуле

В частности, если кривая АВ задана явным уравнением

причем функция g(х) непрерывно дифференцируема на [а, b] и точке А соответствует значение х = а, а точке В — значение х = b, то, принимая х за параметр, получаем

Криволинейные интегралы 1-го рода для пространственных кривых

Определение криволинейного интеграла 1-го рода, сформулированное выше для плоской кривой, дословно переносится на случай, когда функция f(M) задана вдоль некоторой пространственной кривой АВ.

Пусть кривая АВ задана параметрическими уравнениями

Тогда криволинейный интеграл 1-го рода от функции f, взятый вдоль этой кривой, можно свести к определенному интегралу при помоши следующей формулы:

Пример:

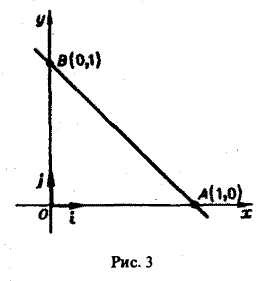
Вычислить криволинейный интеграл

где L — контур треугольника с вершинами в точках O(0,0), A(1,0), B(0, I) (рис. 3).

По свойству аддитивности имеем

Вычислим каждый из интегралов в отдельности. Так как на отрезке OA имеем: 0 ≤ x ≤ 1, у = 0 и dl = dx, то

На отрезке АВ имеем х + у = 1, откуда у = 1 — х, т.е.

причем 0 ≤ х ≤ 1, тогда

Замечание:

При вычислении интегралов

мы воспользовались свойством 1, согласно которому

Криволинейные интегралы 2-го рода

Пусть АВ — гладкая или кусочно-гладкая ориентированная кривая на плоскости хОу и пусть

F(M) = Р(М) i + Q(M) j

— вектор-функция, определенная в некоторой области D, содержащей кривую АВ. Разобьем кривую АВ на части точками

координаты которых обозначим соответственно через

На каждой из элементарных дуг АkАk+1, возьмем произвольно точку Мk(ξk, ηk) и составим сумму

Пусть ∆l — длина наибольшей из дуг АkАk+1.

Определение:

Если при ∆l → 0 сумма (1) имеет конечный предел, не зависящий ни от способа разбиения кривой АВ. ни от выбора точек (ξk, ηk) на элементарных дугах, то этот предел называется криволинейным интегралом 2-го рода от вектор-функции F(M) по кривой АВ и обозначается символом

Так что по определению (2)

Теорема:

Если в некоторой области D, содержащей кривую АВ, функции Р(х,у) и Q(х, у) непрерывны, то криволинейный интеграл 2-го рода

r(М) = xi + yj

— радиус-вектор точки М(х, у). Тогда

dr = i dx + j dy,

и подынтегральное выражение

Р(х, у) dx + Q(x, у) dy

в формуле (2) можно представить в виде скалярного произведения векторов F(Af) и dr. Так что интеграл 2-го рода от вектор-функции

по кривой АВ можно записать коротко так:

Вычисление криволинейного интеграла 2-го рода

Пусть кривая АВ задана параметрическими уравнениями,

где функции φ(t) и ψ(t) непрерывны вместе с производными φ'(t), ψ'(t) на отрезке [to, t1] причем изменению параметра t от to до t1 соответствует движение точки М(х, у) по кривой АВ от точки А к точке В.

Если в некоторой области D, содержащей кривую АВ, функции Р(х, у) и Q(x, у) непрерывны, то криволинейный интеграл 2-го рода

сводится к следующему определенному интегралу:
(3)

Таким образом, вычисление криволинейного интеграла 2-го рода также может быть сведено к вычислению определенного интеграла.

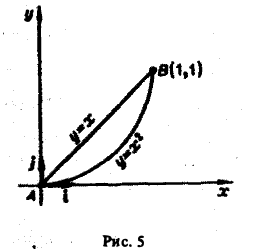
Пример:

1) вдоль прямолинейного отрезка, соединяющего точки A(0,0) и В<1, 1);

2) вдоль параболы у = х , соединяющей те же точки (рис.5).

1) Уравнение линии АВ: у = х (х — параметр, 0 ≤ х ≤ 1), откуда dy = dx. Так что

2) Уравнение линии AB:

dy = 2х dx,

x dy = 2x 2 dx

Рассмотренный пример помазывает, что величина криволинейного интеграла 2-го рода, вообще говоря, зависит от формы пути интегрирования.

Свойства криволинейного интеграла 2-го рода

1. Линейность. Если существуют криволинейные интегралы

то при любых действительных а и β существует и интеграл

2. Аддитивность. Если кривая АВ разбита на части АС и С В и криволинейный интеграл

существует, то существуют интегралы

Криволинейный интеграл второго рода (в отличие от криволинейного интеграла 1-го рода) зависит от того, в каком направлении (от A к В или от В к А) проходится кривая АВ, и меняет знак при изменении направления движения по кривой, т. е.

Замечание:

Последнее свойство cotrmrrayer физической интерпретации криволинейного интеграла 2-го рода как работы силового паля F вдоль некоторого путь: при изменении направления движения по кривой работа силового поля вдоль этой кривой меняет знак на противоположный.

Связь между криволинейными интегралами 1-го и 2-го рода

Рассмотрим криволинейный интеграл 2-го рода

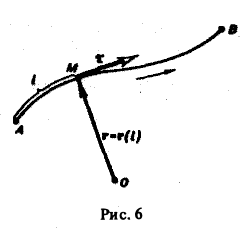
где ориентированная кривая АВ (А — начальная точка, В — конечная точка) задана векторным уравнением

r = r(l)

(здесь l — длина кривой, отсчитываемая в том направлении, в котором ориентирована кривая АВ) (рис. 6).

где т = т(l) — единичный вектор касательной к кривой АВ в точке М(l). Тогда

Заметим, что последний интеграл в этой формуле — криволинейный интеграл 1-го рода. При изменении ориентации кривой АВ единичный вектор касательной т заменяется на противоположный вектор (—т), что влечет изменение знака его подынтегрального выражения и, значит, знака самого интеграла.

Формула Грина

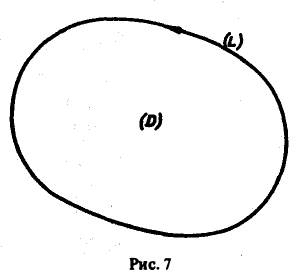
Выведем формулу Грина, связывающую криволинейный интеграл

по границе L некоторой плоской области D с двойным интегралом по этой области.

Теорема:

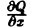
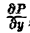
Если в замкнутой области D, ограниченной кусочно-гладким контуром L, функции Р(х, у) и Q<x, у) непрерывны и имеют непрерывные частные производные и то справедливо равенство (формула Грина):

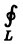
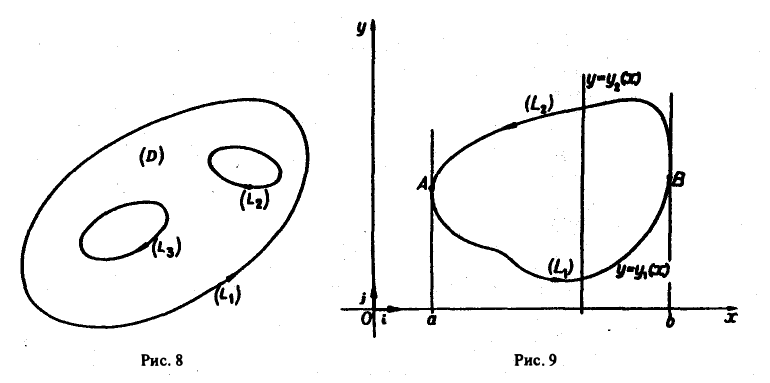
Здесь символ означает интегрирование по границе L области D, причем граница L проходится так, что область D остается слева (рис. 7).

Граница L плоской области D может состоять из одной или нескольких простых замкнутых кривых (компонент). В первом случае она называется односвязной, а во втором — многосвязной. Если граница L состоит из конечного числа кусочно-гладких замкнутых кривых Li, то кривые L, называются связными компонентами границы. На рис. 8 изображена трехсвязная область.

Односвязная область D (область «без дырок») обладает тем свойством, что любая лежащая в ней замкнутая кривая может быть стянута в точку Р ∈ D, оставаясь в процессе стягивания в области D.
Доказательство теоремы проведем для односвязной области.

В силу свойства линейности достаточно доказать, что

Докажем первую из этих формул.

Предположим сначала, что кривая L пересекается каждой прямой, параллельной оси Оу, не более чем в двух точках или по целому отрезку (рис. 9). Если каждая такая прямая пересекает кривую L не более чем в двух точках, то кривую L можно разбить на две части L1 и L2 (верхнюю и нижнюю), каждая из которых проектируется взаимно однозначно на некоторый отрезок [а, b] оси Ох. В силу аддитивности криволинейного интеграла имеем

На каждой из кривых L1 и L2 возьмем в качестве параметра абсциссу х и запишем уравнения этих кривых соответственно в виде

По предположению производная 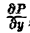непрерывна в D, и значит, в силу известной формулы интегрального исчисления, приращение функции можно записать через интеграл от производной этой функции:

Из формул (4) и (5) получаем

Повторный интеграл в правой части последнего соотношения равен двойному интегралу от функции 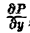по области D, так что окончательно имеем

Формула (2) доказана.

Соотношение (3) доказывается аналогично. Складывая почленно соотношения (2) и (3), получаем формулу Грина (1).

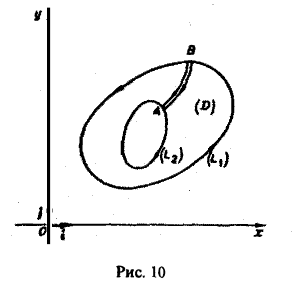
Отметим, что формула Грина имеет место и для более сложных контуров L, и для неодносвязных областей D. Рассмотрим, например, случай двухсвязной области (рис. 10). Сделаем разрез АВ этой области, превращающий ее в односвязную. Тогда

Отсюда, учитывая, что

где интегрирование по кривой L1 ведется в направлении против движения часовой стрелки, а по кривой L2 — в направлении движения часовой стрелки. Отметим, что при этом кривые L1 и L2 проходятся так, что область D остается слева. Такое направление обхода контура принимается за положительное.

Площадь плоской области

Р(х, y) = -y и Q(x,y) = x.

и по формуле Грина (1) получаем

где S — площадь области D.

Отсюда получаем формулу для вычисления площади S плоской области D с помощью криволинейного интеграла по границе L этой области: (7)

Пример:

Вычислить площадь области, ограниченной эллипсом L:

Запишем уравнение эллипса в параметрической форме

Искомая площадь находится no формуле (7), где криволинейный интеграл берется по эллипсу при обходе контура в положительном направлении, что соответствует изменен ию параметра t от 0 до 2 π. Так как

то отсюда получаем, что

Замечание:

Пусть в пространстве задана ориентированная кусочно-гладкая кривая АВ и пусть, кроме того, в некоторой области Ω, содержащей кривую А В, задана вектор-функция

где Р, Q, R — непрерывные в Ω функции. Аналогично плоскому случаю криволинейный интеграл от вектор-функции F по ориентированной кривой АВ определим выражением

Это — криволинейный интеграл 2-го рода в пространстве.

Приложения криволинейных интегралов

Масса кривой

В примере 1 из § 1 было показано, что масса кривой L вычисляется с помощью интеграла 1-го рода

где f(M) — переменная линейная плотность на кривой L. (Мы предполагаем, что f(М) — непрерывная функция на АВ.)

Площадь цилиндрической поверхности

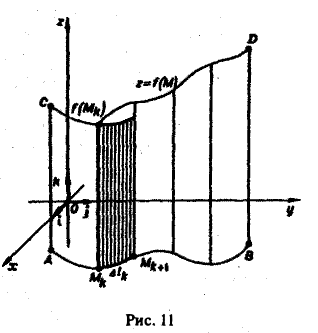
Пусть в плоскости хОу задана некоторая спрямляемая (т. е. имеющая длину) кривая АВ и на этой кривой определена непрерывная функция f(М) ≥ 0. Тогда совокупность точек (х, y, f(x, у)), или (М, f(M)), составит некоторую кривую, лежащую на цилиндрической поверхности, для которой кривая АВ является направляющей, а ее образующая параллельна оси Oz. Требуется определить площадь цилиндрической поверхности ABDC, ограниченной снизу кривой АВ, сверху — кривой z = f(M), где М ∈ АВ, и вертикальными прямыми АС и BD (рис. 11).

Для решения этой задачи поступим так:

1) разобьем кривую АВ на п частей точками

так, как показано на рис. 11;

2) из каждой точки Мk проведем перпендикуляр к плоскости хОу высотой f(Mk) (при этом цилиндрическая поверхность ABDC разобьется на n полосок);

3) каждую полоску заменим прямоугольником с основанием ∆lk, где ∆lk — длина дуги МkМk+1, и высотой, равной значению функции f<M) в какой-нибудь точке этой дуги, например, в точке Мk.

Тогда площадь k-ой полоски будет приближенно равна f(Mk) ∆lk, а площадь всей поверхности ABDC

Это приближенное равенство будет тем точнее, чем мельче будут частичные дуги МkМk+1, на которые разбита кривая АВ. Пусть ∆l — наибольшая из длин ∆lk частичных дуг MkMk+1. Тогда при ∆l —> 0 в пределе получим точное значение искомой площади

Предел справа по определению есть криволинейный интеграл первого рода от функции f(М) по кривой АВ. Итак, (2)

Пример:

Вычислить площадь части боковой поверхности цилиндра

срезанного сверху поверхностью

ху = 2Rz.

Сведем задачу к вычислению криволинейного интеграла 1-го рода от функции

вдоль дуги окружности, расположенной в первой четверти. Будем иметь

Параметрические уравнения линии АВ —

Площадь плоской фигуры

Ранее мы установили, что площадь S плоской фигуры D, ограниченной линией L, вычисляется по формуле

Правая часть есть криволинейный интеграл 2-го рода.

Работа силы:

Пусть в некоторой плоской области D, содержащей кривую АВ, задана сила

F(M) = P(M)i + Q(M)J, (4)

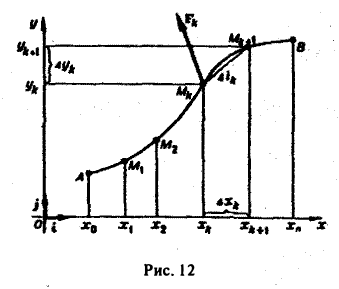
где функции Р(М) и Q(M), а следовательно, и F(M) предполагаются непрерывными функциями точки М. Требуется найти работу силы F, если под действием этой силы материальная точка М, имеющая единичную массу, переместилась из точки А в точку В по кривой АВ.

Для решения этой задачи разделим кривую АВ на п частей точками

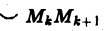
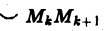
(рис. 12), заменим каждую дугу хордой MkMk+1 и, предполагая для простоты, что на участке кривой (а значит, и на хорде MkMk+1) сила Fk имеет постоянное значение, например, равное ее значению в точке Мk,

получим приближенное выражение работы силы на участке пути :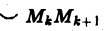

где |Fk| — длина вектора Fk, |∆lk| — длина вектора ∆lk

Из формулы (4) с учетом (5) получим

Так как правая часть формулы (6) есть скалярное произведение векторов Fk и ∆lk, то, учитывая (7) и (8), будем иметь

Суммируя по всем значениям k(k = 0,1,2,…, п — 1), получим величину

приближенно выражающую работу силы F(M) на всем пути от А до В.

Предел этой суммы при ∆хk → 0 и ∆уk → 0 принимают за точное значение работы. Но с другой стороны, предел этой суммы есть криволинейный интеграл 2-го рода от вектор-функции F(M) по кривой АВ. Итак, работа силы вычисляется по формуле
(9)

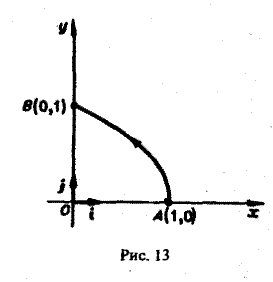
Пример:

Найти работу силы

при перемещении единичной массы по параболе

от точки A(1,0) до точки В(0,1) (рис. 13). 4 Применим формулу (9), положив в ней

то искомую работу можно вычислить так:

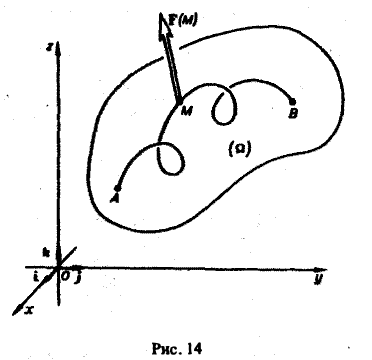
Обобщение на случай пространственной кривой(рис. 14),

Если в некоторой пространственной области Ω, содержащей пространственную кривую АВ, задана сила

F(M) = Р(М)i + Q(M)j + R(M)k,

где Р(М), Q(M) и R(M) — непрерывные функции в области Ω, то работа, совершаемая силой F(М) по перемещению материальной точки М с единичной массой из точки А в точку В по пространственной кривой АВ, равна

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

🎦 Видео

Криволинейный интеграл 1-го рода ★ Криволинейный интеграл по длине дуги ★ ∫(x+y)dsСкачать

Криволинейные интегралы второго рода. Вычисление.Скачать

Вычислить интеграл по заданному контуру. Интегрирование по части окружности и по отрезку прямой.Скачать

Криволинейные интегралы 1-ого родаСкачать

Семинар 8. Криволинейные интегралы.Скачать