Прямые а и б изображенные на рисунке параллельными на самом деле не параллельны чертеж

Презентация была опубликована 8 лет назад пользователемИгорь Недоростков

Похожие презентации

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Презентация на тему: » Графическая работа 1 по теме: «Следствия из аксиом стереометрии» Выполнили: Бахтияров Ринат Берглезов Максим Останина Ирина Попова Дарья.» — Транскрипт:

1 Графическая работа 1 по теме: «Следствия из аксиом стереометрии» Выполнили: Бахтияров Ринат Берглезов Максим Останина Ирина Попова Дарья

2 Выполнил: Бахтияров Ринат 1 α М P MPϵα Прямая MP лежит в плоскости α.

3 Выполнил: Бахтияров Ринат 2 Прямая АВ пересекает плоскость α в точке М. А В М α АВα=М

4 Выполнил: Бахтияров Ринат 3 Плоскость α проходит через прямую а и точку М, не принадлежащую прямой а, и пересекает прямую b в точке М. а b M α bα=M aα M ϵ a

5 Выполнил: Бахтияров Ринат 4 Прямые МС и МВ пересекают плоскость β в одной и той же точке. β М С В МСМВ=М МСβ=М МВβ=М

6 Выполнил: Берглезов Максим 5 Прямые МС и МВ пересекают плоскость γ в разных точках. γ С В М МВγ=В МСγ=С

7 Выполнил: Берглезов Максим 6 Прямые а и b, изображенные на рисунке параллельными, на самом деле не параллельны. а b а ǁ b

8 Выполнил: Берглезов Максим 7 Прямые а и b, изображенные на рисунке пересекающимися, на самом деле не имеют общих точек. а b O α a b

9 Выполнил: Берглезов Максим 8 Плоскость α и β имеют общую прямую а и пересекают прямую КМ соответственно в точках К и М. К М α β а аϵα аϵβ КМα=К КМβ=М

10 Выполнила: Останина Ирина 9 Плоскость α и β пересекаются по прямой с, а плоскость α и γ также пересекаются по этой же прямой с. α β γ с αγ=сαβ=сαγ=сαβ=с

11 Выполнила: Останина Ирина 10 Плоскость α и β пересекаются по прямо МР, а плоскости α и γ пересекаются по другой прямой — прямой МТ. Т Р М β αβ=МР αγ=МТ

12 Выполнила: Останина Ирина 11 Прямые а, b и c имеют общую точку О и лежат в одной плоскости. α О а b c aϵα bϵα cϵα abc=O

13 Выполнила: Останина Ирина 12 Прямые а, b и c имеют общую точку О, но не существует плоскости, в которой лежат все эти три прямые. О а b c abc=O

14 Выполнила: Попова Дарья 13 Плоскости α,β и γ имеют единственную принадлежащею всем трем плоскостям точку О. β О Oϵα Oϵγ Oϵβ

15 Выполнила: Попова Дарья 14 Прямые АВ и МТ таковы, что точка А не принадлежит плоскости ВМТ, а точка В не принадлежит прямой МТ. А В М Т Aϵ(BMT) Bϵ(BMT)

16 Выполнила: Попова Дарья 15 На прямой а, пересекающей плоскость α в точке А, выбраны по разные стороны от А точки М и Т. Прямые ММ 1 и ТТ 1 параллельны между собой и пересекают плоскость α соответственно в точках М 1 и Т 1. α а Т А М М1М1 Т1Т1 aα=A MTϵa ММ 1 ǁТТ 1 ММ 1α=M 1 ТТ 1 α =T 1

17 Выполнила: Попова Дарья 16 Две вершины треугольника АВС лежат в плоскости α, а вершина С не лежат в α. Прямая d пересекает стороны СВ и СА соответственно в точках М и Т, а плоскость α в точке К. α А В М Т К С ABϵα cϵα dCA=T dα=K KϵAB

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Графическая работа для 10 класса
тест по геометрии (10 класс) на тему

Использую после изучения темы.

Видео:№16. Параллельные прямые a и b лежат в плоскости α. Докажите,Скачать

Скачать:

Бесплатный марафон подготовки к ЕГЭ на зимних каникулах

Учи.Дома запускает бесплатный марафон в котором каждый день. В течении 5 дней утром ты будешь получать одно задание по выбранному предмету, а вечером его решение. Твоя задача, успеть выполнение задание до того как получишь ответ.

Бесплатно, онлайн, подготовка к ЕГЭ

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Предварительный просмотр:

Графическая работа № 1 Тема: « Аксиомы стереометрии. Следствия из аксиом»

Сделайте чертежи, используя данные в задачах обозначения.

1. Прямая ΜΡ лежит в плоскости α.

2. Прямая АВ пересекает плоскость α в точке М.

3. Плоскость проходит через прямую а и точку М, не лежащую на прямой а , и пересекает прямую b в точке М.

4. Прямые МС и МВ пересекают плоскость β в разных точках.

5. Прямые МС и МВ пересекают плоскость γ в одной и той же точке.

6. Плоскости α и β имеют общую прямую а и пересекают прямую КМ соответственно в точках К и М.

7. Прямые а , b и с имеют общую точку О и лежат в одной плоскости.

8. Прямые а , b и с имеют общую точку О, но не существует плоскости, в которой лежат все эти три прямые.

9. На прямой а , пересекающей плоскость α в точке А, выбраны по разные стороны от А точки М и Т. Прямые ММ 1 и ТТ 1 параллельны между собой и пересекают плоскость α соответственно в точках М 1 и Т 1 .

10. Плоскости α, β и γ имеют единственную принадлежащую все трём плоскостям точку О.

11. Плоскости α и β пересекаются по прямой с, а плоскости α и γ также пересекаются по этой же прямой с.

12.Две вершины треугольника АВС лежат в плоскости α, а вершина С не лежит в α. Прямая d пересекает стороны СВ и СА соответственно в точках М и Т, а плоскость α в точке К.

13. Прямые а и b , изображённые на рисунке параллельными, а на самом деле не параллельны.

14. Прямые а и b , изображённые на рисунке пересекающимися, на самом деле не имеют общих точек.

Графическая работа № 2 Тема: «Параллельность в пространстве»

Сделайте чертежи, используя данные в задачах обозначения.

1. Прямая МР параллельна плоскости α, а прямая МТ пересекает эту плоскость в точке Т.

2. Плоскость α пересекает три параллельных прямых а, b и c соответственно в точках А, В и С, лежащих на одной прямой.

3. Плоскость α пересекает три параллельных прямых а, b и c соответственно в вершинах треугольника АВС.

4. Основание AD трапеции ABCD лежит на плоскости α, а прямые ВК и СК пересекают эту плоскость соответственно в точках В 1 и С 1 .

5. Плоскость α проходит через середины сторон АВ и АС треугольника АВС и не содержит вершины А.

6. Прямая МР параллельна плоскости α, а плоскость РМТ пересекает плоскость α по прямой КТ.

7. Прямая а параллельна каждой из пересекающихся плоскостей α и β.

8. Прямая а параллельна каждой из параллельных плоскостей α и β.

9. Плоскости α и β имеют общую прямую а , плоскости α и γ общую прямую b, а плоскости β и γ общую прямую с. Прямые а и b пересекаются в точке М.

10. Плоскости α и β имеют общую прямую а , плоскости α и γ общую прямую b, а плоскости β и γ общую прямую с. Прямые а и b параллельны.

11. Плоскости α и β имеют общую прямую а , плоскости α и γ общую прямую b, а плоскости β и γ параллельны.

12. Сторона ВС треугольника АВС лежит в плоскости α, через вершину А и точку М – середину стороны АС проведены соответственно плоскости β и γ, пересекающие плоскость треугольника АВС по прямым АК и МТ.

Графическая работа № 3 Тема: «Перпендикулярность в пространстве»

Сделайте чертежи, используя данные в задачах обозначения.

1. Прямая АМ перпендикулярна плоскости треугольника АВС.

2. Прямая ОК проходит через точку О пересечения диагоналей квадрата АВСD и перпендикулярна его плоскости.

3. Прямая ОК проходит через точку О пересечения диагоналей трапеции АВСD (AD – большее основание) и перпендикулярна её плоскости.

4. Плоскости равносторонних треугольников АВС и АВК перпендикулярны.

5. Прямые ОМ, ОК и ОТ попарно перпендикулярны друг другу.

6. Плоскость КТС перпендикулярна плоскостям ТМС и ТВК.

7. Прямая КМ перпендикулярна плоскости квадрата КТРС, а прямая МА перпендикулярна прямой РТ.

8. Прямая КМ перпендикулярна плоскости квадрата КРТС, а прямая МА перпендикулярна прямой СТ.

9. Вершина А треугольника АВС лежит в плоскости α, параллельной прямой ВС. Прямые ВВ 1 и СС 1 перпендикулярны плоскости α и пересекают её соответственно в точках В 1 и С 1 .

10. Прямая КМ перпендикулярна плоскости равнобедренного треугольника АВС (АВ = ВС) и пересекает в точке Т, середине КМ. Их точек К и М на прямую ВС опущены перпендикуляры.

Графическая работа № 1 Тема: « Аксиомы стереометрии. Следствия из аксиом»

Сделайте чертежи, используя данные в задачах обозначения.

1. Прямая ΜΡ лежит в плоскости α.

2. Прямая АВ пересекает плоскость α в точке М.

3. Плоскость проходит через прямую а и точку М, не лежащую на прямой а , и пересекает прямую b в точке М.

4. Прямые МС и МВ пересекают плоскость β в разных точках.

5. Прямые МС и МВ пересекают плоскость γ в одной и той же точке.

6. Плоскости α и β имеют общую прямую а и пересекают прямую КМ соответственно в точках К и М.

7. Прямые а , b и с имеют общую точку О и лежат в одной плоскости.

8. Прямые а , b и с имеют общую точку О, но не существует плоскости, в которой лежат все эти три прямые.

9. На прямой а , пересекающей плоскость α в точке А, выбраны по разные стороны от А точки М и Т. Прямые ММ 1 и ТТ 1 параллельны между собой и пересекают плоскость α соответственно в точках М 1 и Т 1 .

10. Плоскости α, β и γ имеют единственную принадлежащую все трём плоскостям точку О.

11. Плоскости α и β пересекаются по прямой с, а плоскости α и γ также пересекаются по этой же прямой с.

12.Две вершины треугольника АВС лежат в плоскости α, а вершина С не лежит в α. Прямая d пересекает стороны СВ и СА соответственно в точках М и Т, а плоскость α в точке К.

13. Прямые а и b , изображённые на рисунке параллельными, а на самом деле не параллельны.

14. Прямые а и b , изображённые на рисунке пересекающимися, на самом деле не имеют общих точек.

Видео:Математика 10 Класс (Алгебра и Геометрия)Скачать

Прямые а и б изображенные на рисунке параллельными на самом деле не параллельны чертеж

Проекцией прямой, которая не перпендикулярна плоскости проекций, является прямая. Её положение определяется двумя точками, следовательно, для того чтобы построить проекцию прямой, достаточно построить проекции двух её точек.

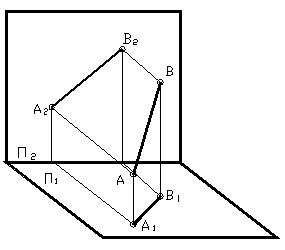
Рисунок 8

а) Прямой общего положения называется прямая, которая не параллельна и не перпендикулярна ни одной из плоскости проекций. Пример такой прямой изображён на рисунке 8. Комплексный чертёж этой прямой будет выглядеть следующим образом.

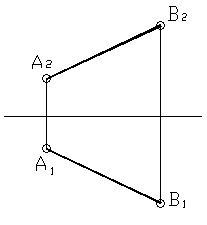
Рисунок 9

б) Прямые частного положения – это прямые, занимающие по отношению к плоскостям проекций особое положение, т.е. либо параллельные, либо перпендикулярные плоскостям проекций.

Первый подкласс прямых частного положения – прямые уровня. Это прямые, параллельные какой-либо плоскости проекций.

Горизонталь – прямая параллельная горизонтальной плоскости П1. Комплексный чертёж такой прямой изображён на рисунке 10.

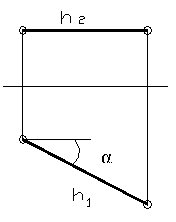
Рисунок 10

Фронтальная проекция горизонтали всегда параллельна прямой Х, а угол между осью Х и горизонтальной проекцией горизонтали составляет угол между прямой и фронтальной плоскостью проекций. Символическая запись: h // П1; α = Ð h П2.

Фронталь – прямая параллельная фронтальной плоскости П2. Комплексный чертёж фронтали изображён на рисунке 11.

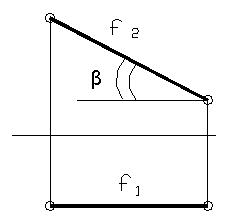
Рисунок 11

Горизонтальная проекция фронтали параллельна оси Х, а угол β — угол наклона фронтали к горизонтальной плоскости проекций; f₂ // П2, β= Ð f1 П1.

Профильная прямая – это прямая, параллельная профильной плоскости П 3 . Комплексный чертёж профильной прямой изображён на рисунке 12. Горизонтальная и фронтальная проекции профильной прямой перпендикулярны оси Х, а углы α и β — соответственно, углы наклона прямой к плоскостям П 1 и П2.

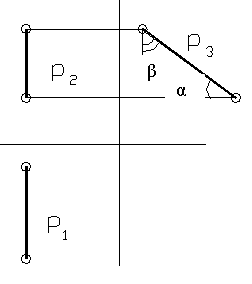
Рисунок 12.

Истинная величина прямых уровня или, так называемая натуральная величина, отображена на тех плоскостях, которым параллельны эти прямые.

Второй подкласс прямых частного положения – проецирующие прямые. Это прямые, перпендикулярные какой-либо плоскости проекций. К таким прямым относятся: горизонтально–проецирующая, фронтально-проецирующая и профильно-проецирующая прямые.

Их комплексные чертежи изображены соответственно на рисунке 13 (а, б, в).

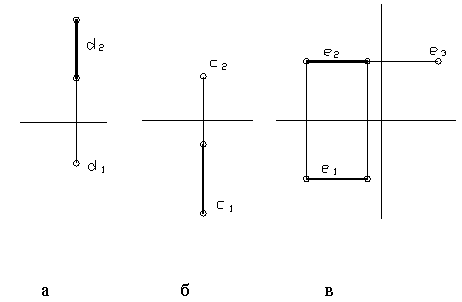
Рисунок 13

Натуральная величина горизонтально-проецирующей прямой – её фронтальная проекция, фронтально-проецирующей прямой – её горизонтальная проекция, а профильно-проецирующей прямой – её горизонтальная и фронтальная проекции.

а) три точки, не лежащие на одной прямой;

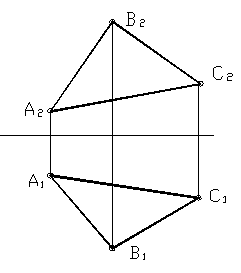
Рисунок 14

б) прямая и точка, не лежащая на ней;

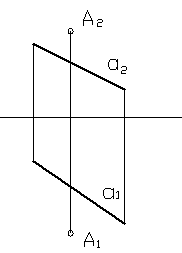
Рисунок 15

в) две параллельные прямые;

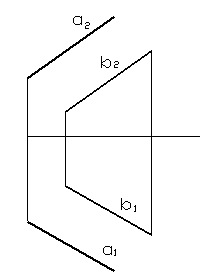
Рисунок 16

г) две пересекающиеся прямые;

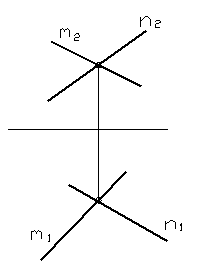
Рисунок 17

д) плоская фигура (многоугольник, круг и т.д.).

Плоскость общего положения не параллельна и не перпендикулярна ни одной из плоскостей проекций.

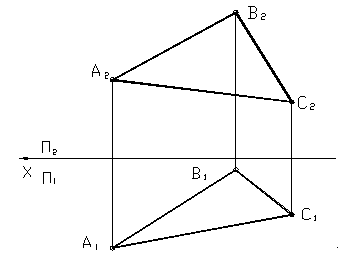
Рисунок 18

Плоскости частного положения аналогично прямой подразделяются на плоскости уровня и проецирующие плоскости. На рисунке 19 (а,б,в) изображены, соответственно, горизонтальная, фронтальная и профильная плоскости. Причём горизонтальная плоскость задана двумя параллельными прямыми, фронтальная и профильная плоскости – двумя пересекающимися прямыми.

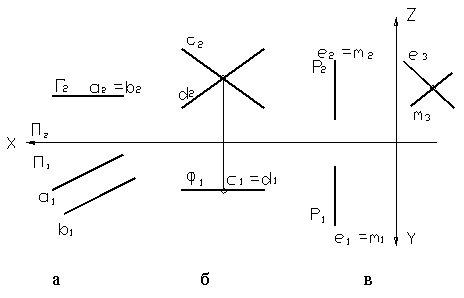
Рисунок 19

На рисунке 20 (а, б, в) показаны проецирующие плоскости. Горизонтально-проецирующая (рис. 20а) задана треугольником, фронтально-проецирующая (рис. 20б) — параллельными прямыми и профильно-проецирующая (рис. 20в) – пересекающимися прямыми.

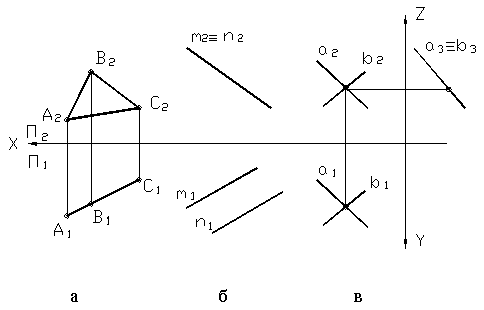
Рисунок 20

1. Как образуется комплексный чертеж прямой линии?

2. Прямые какого положения вы знаете?

3. Назовите прямые уровня.

4. Как называется прямая, проекцией которой на горизонтальной плоскости будет точка?

5. Перечислите способы задания плоскости.

6. Дайте определение плоскости общего положения.

7. Какие бывают плоскости частного положения? Как они называются и как выглядят на комплексном чертеже?

© ФГБОУ ВПО Красноярский государственный аграрный университет

📹 Видео

ГЕОМЕТРИЯ 10 класс : Параллельность прямых, прямой и плоскостиСкачать

Перпендикулярные прямые. 6 класс.Скачать

№93. Прямые а и b параллельны. Через точку М прямой a проведена прямая MN, отличная от прямой а и неСкачать

10 класс, 3 урок, Некоторые следствия из аксиомСкачать

№188. Отрезки АВ и CD пересекаются в их общей середине. Докажите, что прямые АССкачать

В-2 № 1-100 - Геометрия 7 класс Мерзляк дидактические материалыСкачать

Разбор работы по геометрии 10-го класса. Математическая вертикаль.Скачать

Стереометрия 10 класс. Часть 2 | Математика | TutorOnlineСкачать

№142. Концы отрезка отстоят от плоскости α на расстояниях 1 см и 4 см. Найдите расстояниеСкачать

№91. Через каждую из двух параллельных прямых a и b и точку М, не лежащую в плоскости этих прямыхСкачать

ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ 7 класс геометрия АтанасянСкачать

параллельные прямыеСкачать

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. Видеоурок | ГЕОМЕТРИЯ 7 классСкачать