Окружность доказать что ad bc

Видео:№144. Отрезки АВ и CD — диаметры окружности. Докажите, что: а) хорды BD и АС равны; б) хорды AD и ВССкачать

Ваш ответ

Видео:Окружность. 7 класс.Скачать

решение вопроса

Видео:№117. В тетраэдре ABCD известно, что BC⊥AD. Докажите, что AD⊥MN, где М и N — середины реберСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,835
• разное 16,824

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать

Окружность доказать что ad bc

Около окружности с центром O описана трапеция ABCD с основаниями AD и BC.

а) Докажите, что AB — диаметр окружности, описанной около треугольника AOB.

б) Найдите отношение площади четырёхугольника, вершины которого — точки касания окружности со сторонами трапеции, к площади самой трапеции ABCD, если известно, что AB = CD, а основания трапеции относятся как 1 : 2.

а) Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому AO и BO — биссектрисы углов BAD и ABC соответственно. Следовательно,

Если угол, вписанный в окружность, прямой, то он опирается на диаметр. Следовательно, отрезок AB — диаметр окружности, описанной около треугольника AOB.

б) Пусть K, L, M и N — точки касания окружности со сторонами AB, BC, CD и AD данной трапеции соответственно. Тогда L — середина основания BC, потому что углы ABC и BCD равны, углы OBL и OCL равны и прямоугольные треугольники OBL и OCL равны по общему катету OL и острому углу. Аналогично N — середина основания AD. Обозначим CM = CL = BL = BK = x; DM = DN = AN = AK = y (x

Пусть площадь трапеции ABCD равна S, а площадь четырёхугольника KLMN равна S₁. Тогда

а так как диагонали KM и LN четырёхугольника KLMN перпендикулярны, получаем, что

Следовательно,

Ответ: б)

Критерии оценивания выполнения задания	Баллы
Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б)	3
Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки	2
Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Видео:№189. Используя данные рисунка 108, докажите, что BC||AD.Скачать Решение задачи №16 с настоящего ЕГЭ 2018 Условие задачи Четырёхугольник ABCD вписан в окружность радиуса R = 8. Известно, что AB=BC=CD=12. а) Докажите,что прямые BC и AD параллельны. Решение а) Докажем, что BC∥AD. Равные дуги стягиваются равными хордами. Дуги АВ и CD, стягиваемые равными хордами АВ и CD, равны. Значит, ∠АСВ=∠CAD — как опирающиеся на равные дуги. Эти углы — накрестлежащие при прямых BC и AD и секущей АС. б) Найдем AD, если АВ=ВС=CD=12, R=8. эж По теореме синусов, — так как опираются на равные хорды. Так как ABCD — равнобедренная трапеция, По теореме синусов из треугольника CDA: По теореме косинусов из △ACD: ‘ alt=’sin varphi =displaystyle frac = >’ /> x=12 или х =9. Если х=12, то ABCD — квадрат (ромб, вписанный в окружность). Тогда условие R=8 не выполняется. 📽️ Видео Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать Окружность, диаметр, хорда геометрия 7 классСкачать ОГЭ по математике. Задание 15Скачать Задание 16 (В1) ОГЭ по математике ▶ №11 (Минутка ОГЭ)Скачать В окружности проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину угла OAB.Скачать 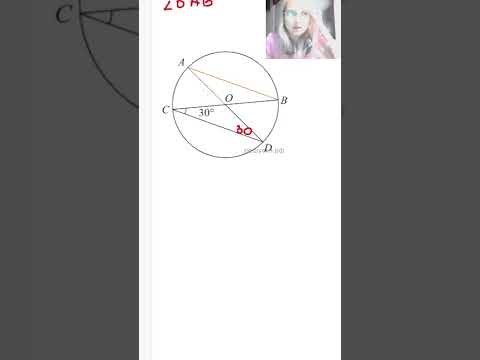№ 144 - Геометрия 7-9 класс АтанасянСкачать В четырехугольник ABCD вписана окружность, AB = 10, BC = 11 и CD = 15. Найдите четвертую сторону.Скачать Всё про углы в окружности. Геометрия | МатематикаСкачать Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать №137. На рисунке 53 (с. 31) BC=AD, AB = CD. Докажите, что ∠B=∠D.Скачать Если в четырёхугольник можно вписать окружностьСкачать В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 30°.ОГЭ МатематикаСкачать 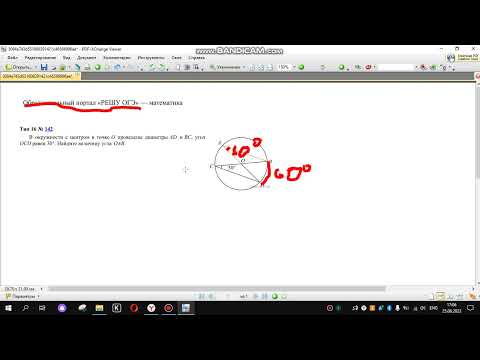Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать 7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать Поделиться или сохранить к себе: Смотрите также Ящик тянут по земле по горизонтальной окружности длиной 60 Ящик тянут по земле по горизонтальной окружности длиной 40 Ящик тянут по земле по горизонтальной окружности диаметром 20 Ящик тянут по земле за веревку по горизонтальной окружности длиной Ящик тянут по земле за веревку по горизонтальной окружности диаметром Электрон равномерно движется по окружности в однородном магнитном поле Электрон и протон ускоренные разностью потенциалов движутся по окружности Шарик скатывается по желобу изогнутому в виде дуги окружности