Прямая по отношению к которой параллельны все лучи после прохождения через линзу

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: линзы, оптическая сила линзы

Взгляните ещё раз на рисунки линз из предыдущего листка: эти линзы обладают заметной толщиной и существенной кривизной своих сферических границ. Мы намеренно рисовали такие линзы — чтобы основные закономерности хода световых лучей проявились как можно более чётко.

Видео:Ход лучей через линзыСкачать

Понятие тонкой линзы.

Теперь, когда эти закономерности достаточно ясны, мы рассмотрим очень полезную идеализацию, которая называется тонкой линзой.
В качестве примера на рис. 1 приведена двояковыпуклая линза; точки и являются центрами её сферических поверхностей, и — радиусы кривизны этих поверхностей. — главная оптическая ось линзы.

Рис. 1. К определению тонкой линзы

Так вот, линза считается тонкой, если её толщина очень мала. Нужно, правда, уточнить: мала по сравнению с чем?

Во-первых, предполагается, что и . Тогда поверхности линзы хоть и будут выпуклыми, но могут восприниматься как «почти плоские». Этот факт нам очень скоро пригодится.
Во-вторых, , где — характерное расстояние от линзы до интересующего нас предмета. Собственно, лишь в таком случае мы и
сможем корректно говорить о «расстоянии от предмета до линзы», не уточняя, до какой именно точки линзы берётся это самое расстояние.

Мы дали определение тонкой линзы, имея в виду двояковыпуклую линзу на рис. 1 . Это определение без каких-либо изменений переносится на все остальные виды линз. Итак: линза является тонкой, если толщина линзы много меньше радиусов кривизны её сферических границ и расстояния от линзы до предмета.

Условное обозначение тонкой собирающей линзы показано на рис. 2 .

Рис. 2. Обозначение тонкой собирающей линзы

Условное обозначение тонкой рассеивающей линзы показано на рис. 3 .

Рис. 3. Обозначение тонкой рассеивающей линзы

В каждом случае прямая — это главная оптическая ось линзы, а сами точки — её
фокусы. Оба фокуса тонкой линзы расположены симметрично относительно линзы.

Видео:Ход лучей в собирающей линзеСкачать

Оптический центр и фокальная плоскость.

Точки и , обозначенные на рис. 1 , у тонкой линзы фактически сливаются в одну точку. Это точка на рис. 2 и 3 , называемая оптическим центром линзы. Оптический центр находится на Пересечении линзы с её главной оптической осью.

Расстояние от оптического центра до фокуса называется фокусным расстоянием линзы. Мы будем обозначать фокусное расстояние буквой . Величина , обратная фокусному расстоянию, есть оптическая сила — линзы:

Оптическая сила измеряется в диоптриях (дптр). Так, если фокусное расстояние линзы равно 25 см, то её оптическая сила:

Продолжаем вводить новые понятия. Всякая прямая, проходящая через оптический центр линзы и отличная от главной оптической оси, называется побочной оптической осью . На рис. 4 изображена побочная оптическая ось — прямая .

Рис. 4. Побочная оптическая ось, фокальная плоскость и побочный фокус

Плоскость , проходящая через фокус перпендикулярно главной оптической оси, называется фокальной плоскостью. Фокальная плоскость, таким образом, параллельна плоскости линзы. Имея два фокуса, линза соответственно имеет и две фокальных плоскости, расположенных симметрично относительно линзы.

Точка , в которой побочная оптическая ось пересекает фокальную плоскость, называется побочным фокусом. Собственно, каждая точка фокальной плоскости (кроме ) есть побочный фокус — мы ведь всегда сможем провести побочную оптическую ось, соединив данную точку с оптическим центром линзы. А сама точка — фокус линзы — в связи с этим называется ещё главным фокусом.

То, что на рис. 4 изображена собирающая линза, никакой роли не играет. Понятия побочной оптической оси, фокальной плоскости и побочного фокуса совершенно аналогично определяются и для рассеивающей линзы — с заменой на рис. 4 собирающей линзы на рассеивающую.

Теперь мы переходим к рассмотрению хода лучей в тонких линзах. Мы будем предполагать, что лучи являются параксиальными, то есть образуют достаточно малые углы с главной оптической осью. Если параксиальные лучи исходят из одной точки, то после прохождения линзы преломлённые лучи или их продолжения также пересекаются в одной точке. Поэтому изображения предметов, даваемые линзой, в параксиальных лучах получаются весьма чёткими.

Видео:Линзы, оптическая сила линзы, формула тонкой линзы.Построение изображений в линзах. 8 класс.Скачать

Ход луча через оптический центр.

Как мы знаем из предыдущего раздела, луч, идущий вдоль главной оптической оси, не преломляется. В случае тонкой линзы оказывается, что луч, идущий вдоль побочной оптической оси, также не преломляется!

Объяснить это можно следующим образом. Вблизи оптического центра обе поверхности линзы неотличимы от параллельных плоскостей, и луч в данном случае идёт как будто через плоскопараллельную стеклянную пластинку (рис. 5 ).

Рис. 5. Ход луча через оптический центр линзы

Угол преломления луча равен углу падения преломлённого луча на вторую поверхность. Поэтому второй преломлённый луч выходит из плоскопараллельной пластинки параллельно падающему лучу . Плоскопараллельная пластинка лишь смещает луч, не изменяя его направления, и это смещение тем меньше, чем меньше толщина пластинки.

Но для тонкой линзы мы можем считать, что эта толщина равна нулю. Тогда точки фактически сольются в одну точку, и луч окажется просто продолжением луча . Вот поэтому и получается, что луч, идущий вдоль побочной оптической оси, не преломляется тонкой линзой (рис. 6 ).

Рис. 6. Луч, идущий через оптический центр тонкой линзы, не преломляется

Это единственное общее свойство собирающих и рассеивающих линз. В остальном ход лучей в них оказывается различным, и дальше нам придётся рассматривать собирающую и рассеивающую линзу по отдельности.

Видео:Ход лучей в рассеивающей линзеСкачать

Ход лучей в собирающей линзе.

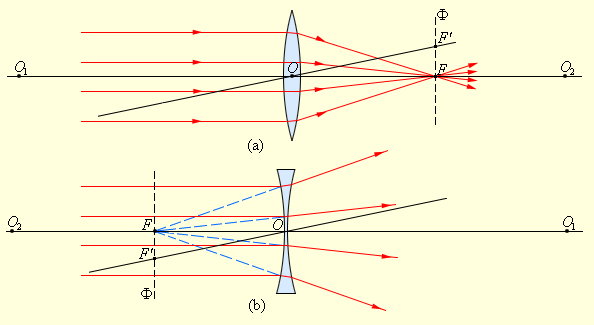
Как мы помним, собирающая линза называется так потому, что световой пучок, параллельный главной оптической оси, после прохождения линзы собирается в её главном фокусе (рис. 7 ).

Рис. 7. Параллельный пучок собирается в главном фокусе

Пользуясь обратимостью световых лучей, приходим к следующему выводу: если в главном фокусе собирающей линзы находится точечный источник света, то на выходе из линзы получится световой пучок, параллельный главной оптической оси (рис. 8 ).

Рис. 8. Преломление пучка, идущего из главного фокуса

Оказывается, что пучок параллельных лучей, падающих на собирающую линзу наклонно, тоже соберётся в фокусе — но в побочном. Этот побочный фокус отвечает тому лучу, который проходит через оптический центр линзы и не преломляется (рис. 9 ).

Рис. 9. Параллельный пучок собирается в побочном фокусе

Теперь мы можем сформулировать правила хода лучей в собирающей линзе. Эти правила вытекают из рисунков 6-9 ,

1. Луч, идущий через оптический центр линзы, не преломляется.
2. Луч, идущий параллельно главной оптической оси линзы, после преломления пойдёт через главный фокус (рис. 10 ).

Рис. 10. К правилу 2

3. Если луч падает на линзу наклонно, то для построения его дальнейшего хода мы проводим побочную оптическую ось, параллельную этому лучу, и находим соответствующий побочный фокус. Вот через этот побочный фокус и пойдёт преломлённый луч (рис. 11 ).

Рис. 11. К правилу 3

В частности, если падающий луч проходит через фокус линзы, то после преломления он пойдёт параллельно главной оптической оси.

Видео:8 класс, 29 урок, Линзы. Построение изображений в линзахСкачать

Ход лучей в рассеивающей линзе.

Переходим к рассеивающей линзе. Она преобразует пучок света, параллельный главной оптической оси, в расходящийся пучок, как бы выходящий из главного фокуса (рис. 12 )

Рис. 12. Рассеяние параллельного пучка

Наблюдая этот расходящийся пучок, мы увидим светящуюся точку, расположенную в фокусе позади линзы.

Если параллельный пучок падает на линзу наклонно, то после преломления он также станет расходящимся. Продолжения лучей расходящегося пучка соберутся в побочном фокусе , отвечающем тому лучу, который проходит через через оптический центр линзы и не преломляется (рис. 13 ).

Рис. 13. Рассеяние наклонного параллельного пучка

Этот расходящийся пучок создаст у нас иллюзию светящейся точки, расположенной в побочном фокусе за линзой.

Теперь мы готовы сформулировать правила хода лучей в рассеивающей линзе. Эти правила следуют из рисунков 6, 12 и 13 .

1. Луч, идущий через оптический центр линзы, не преломляется.
2. Луч, идущий параллельно главной оптической оси линзы, после преломления начнёт удаляться от главной оптической оси; при этом продолжение преломлённого луча пройдёт через главный фокус (рис. 14 ).

Рис. 14. К правилу 2

3. Если луч падает на линзу наклонно, то мы проводим побочную оптическую ось, параллельную этому лучу, и находим соответствующий побочный фокус. Преломлённый луч пойдёт так, словно он исходит из этого побочного фокуса (рис. 15 ).

Рис. 15. К правилу 3

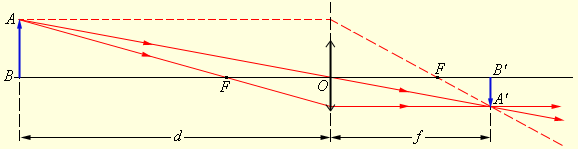
Пользуясь правилами хода лучей 1–3 для собирающей и рассеивающей линзы, мы теперь научимся самому главному — строить изображения предметов, даваемые линзами.

Видео:Урок 209 (осн). Сферические линзы. Основные определенияСкачать

Построение изображения в линзах

Вы уже знаете, что линзы — это прозрачные тела, которые фокусируют (собирают) или рассеивают свет. Но каковы характеристики изображений, создаваемых линзами, и, как и в случае с зеркалами, можно ли их построить?

Видео:Щелчок по физике | Оптика. Законы отражения и преломления. Линзы - Теория. Первая часть (Ролик)Скачать

Оптические характеристики линз

Основная функция линзы в оптической системе заключается в фокусировке или рассеивании падающих световых лучей симметрично относительно оптической оси (см. рисунок 1). В случае двояковыпуклой или двояковогнутой линзы оптическая ось — это линия, соединяющая центры сфер, ограничивающих линзу. Эта ось также является осью симметрии линзы.

Рис. 1. Оптическая ось двояковыпуклой линзы

На оптической оси находится центр линзы — его можно определить графически, как показано на рисунке 2 ниже.

Рис. 2. Метод определения центра двояковыпуклой линзы

При прохождении через линзу свет преломляется дважды: один раз, когда он входит в линзу, и второй раз, когда он выходит из нее.

Когда лучи света, идущие параллельно оптической оси, проходят через собирающую линзу, они пересекаются в точке на оптической оси. Эта точка называется фокусом линзы и обозначается буквой F. Расстояние этой точки от центра S линзы называется фокусным расстоянием f (см. рисунок 3).

Рис. 3. Фокус F и фокусное расстояние f собирающей линзы

Помните! Фокусная точка (F) собирающей линзы — это точка пересечения всех лучей светового пучка после его прохождения через линзу, которые до попадания в линзу шли параллельно ее оптической оси.

Фокусное расстояние (f) линзы — это расстояние от фокусной точки (F) до центра линзы (S).

В случае рассеивающей линзы падающий пучок света расходится — лучи света, входящие в линзу, рассеиваются таким образом, что их продолжения пересекаются в одной точке. Это называется мнимым (кажущимся) фокусом рассеивающей линзы (см. рисунок 4). Он расположен на той же стороне линзы, откуда исходили лучи.

Видео:Физика 11 класс (Урок№13 - Линза. Построение изображения в линзе.)Скачать

Как формируется изображение с помощью собирающей линзы?

Чтобы увидеть, какие изображения мы получаем с помощью собирающей линзы, давайте проведем эксперимент.

Опыт 1. Наблюдение изображений, создаваемых линзой.

Что вам понадобится?

• фонарик;
• кусок черного картона размером больше стекла фонарика;
• ножницы;
• скотч (липкая лента);
• большая лупа;
• белая картонная коробка (экран).

Инструкция.

1. Вырежьте стрелку в черной картонной коробке.
2. С помощью скотча приклейте черный картон к экрану фонарика.
3. Расположите лупу, фонарь и экран на оптической оси лупы.
4. Измените положение фонаря и экрана для получения четкого изображения.

Какой вывод получится?

Изменяя положение экрана и фонарика относительно лупы, вы получите различные изображения — однократно увеличенное, однократно уменьшенное, перевернутое и прямое. Как вы заметите, собирающая линза не обязательно увеличивает наблюдаемый объект. Почему это происходит?

Как и в случае с зеркалами, геометрические построения изображений с использованием лучей (см. рисунок 5), характерных для линз, окажутся полезными для ответа на вопрос, поставленный в резюме эксперимента.

Рис. 5. Лучи, используемые для построения изображения в собирающих линзах

Когда нам нужно построить изображение с помощью собирающей линзы, мы обычно выбираем два из трех перечисленных ниже лучей:

1. луч, параллельный оптической оси — после прохождения через линзу он проходит через фокус;
2. луч, проходящий через центр линзы — после прохождения через линзу его направление (путь) не меняется;
3. луч, проходящий через фокусную точку — после прохождения через линзу выходит параллельно оптической оси.

Последнее предложение справедливо для тонких линз, которые мы и будем использовать в наших экспериментах. Затем мы проигнорируем толщину линзы и нарисуем ее в виде отрезка, заканчивающегося стрелками.

Изображение точки образуется при пересечении как минимум двух лучей или их продолжений.

Сводная информация о положении изображения в зависимости от положения объекта и характеристиках получаемых изображений приведена в таблице 1 ниже.

Положение объекта, x	Положение изображения, y	Особенности изображения
x > 2f	f x > f	y > 2f	Перевернутое, действительное, увеличенное
x = f	лучи проходят через линзу и параллельны друг другу	Без изображения
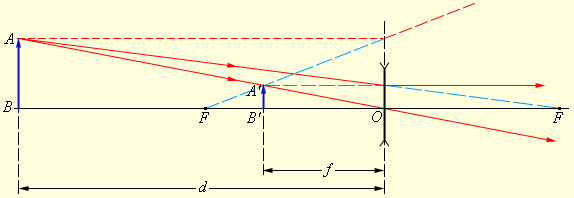
x Таблица 1. Характеристики изображения, создаваемого собирающей линзой Из таблицы 1 можно сделать вывод, что характеристики изображения, формируемого в собирающей линзе, зависят от расстояния объекта от линзы. Помните! Реальное изображение точки формируется там, где пересекаются лучи, преломленные через линзу. Однако часто бывает так, что преломленные лучи расходятся. Тогда их продолжения всегда пересекаются, и получается мнимое (иллюзорное) изображение. Если преломленные лучи параллельны друг другу, изображение вообще не образуется. Видео:ЛИНЗА В ФИЗИКЕ часть 1 // Физика 8 класс: Фокусное расстояние и Преломление светаСкачать Как создается изображение при использовании рассеивающей линзы? В случае с рассеивающей линзой построение изображения несколько иное. Пучок лучей, падающих параллельно линзе после ее выхода, является расходящимся. Как уже говорилось, пересекаются только продолжения лучей, преломленных в так называемой мнимой фокусной точке (см. рисунок 6). Рис. 6. Лучи, используемые для построения изображения в рассеивающих линзах Для построения изображения в рассеивающей линзе (как и в собирающей) достаточно двух лучей: падающий луч, параллельный оптической оси — после прохождения через линзу падающий луч движется таким образом, что его продолжение проходит через мнимую фокусную точку; луч, проходящий через центр линзы — при прохождении через линзу он не меняет направления. 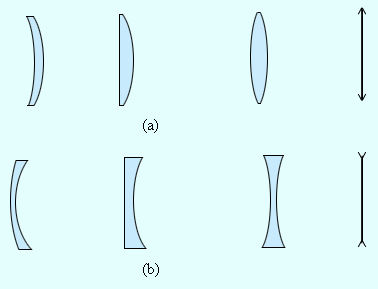Помните! В рассеивающей линзе результирующее изображение всегда прямое, уменьшенное и мнимое. Видео:Урок 211 (осн). Задачи на построение изображений с помощью линзСкачать Тонкие линзы Линза – это прозрачное тело, имеющая 2 сферические поверхности. Она, является тонкой, если ее толщина меньше радиусов кривизны сферических поверхностей. Линза — это составляющая часть почти каждого оптического прибора. Линзы бывают по своему определению собирающие и рассеивающие (рис. 3 . 3 . 1 ). Собирающая линза — это линза, которая в середине толще, чем по краям. Линза, имеющая большую толщину по краям, называется рассеивающей. Рисунок 3 . 3 . 1 . Собирающие ( a ) и рассеивающие ( b ) линзы и их условные обозначения. Главная оптическая ось – это прямая, которая проходит через центры кривизны O 1 и O 2 сферических поверхностей. В тонкой линзе главная оптическая ось пересекается в одной точке – оптическом центре линзы O . Световой луч проходит через оптический центр линзы, не отклоняясь от своего первоначального направления. Побочные оптические оси – это прямые, проходящие через оптический центр. Если к линзе направить пучок лучей, которые расположены параллельно главной оптической оси, тогда после прохождения через линзу лучи (либо их продолжения) сосредоточатся в одной точке F . Эта точка получила название главный фокус линзы. Тонкая линза имеет два главных фокуса, которые располагаются симметрично на главной оптической оси по отношению к линзе. Фокус собирающей линзы – действительный, а у рассеивающей – мнимый. Пучки лучей, параллельные одной из всей совокупности побочных оптических осей, после прохождения через линзу тоже нацелены на точку F ‘ , расположенную на пересечении побочной оси с фокальной плоскостью Ф . Фокальная плоскость – это плоскость, перпендикулярная главной оптической оси и проходящая через главный фокус (рис. 3 . 3 . 2 ). Расстояние между главным фокусом F и оптическим центром линзы О , называется фокусным ( F ) . Рисунок 3 . 3 . 2 . Преломление параллельного пучка лучей в собирающей ( a ) и рассеивающей ( b ) линзах. O 1 и O 2 – центры сферических поверхностей, O 1 O 2 – главная оптическая ось, О – оптический центр, F – главный фокус, F ‘ – фокус, O F ‘ – побочная оптическая ось, Ф – фокальная плоскость. Главным свойством линз является способность передавать изображения предметов. Они, в свою очередь, бывают: Действительные и мнимые; Прямые и перевернутые; Увеличенные и уменьшенные. 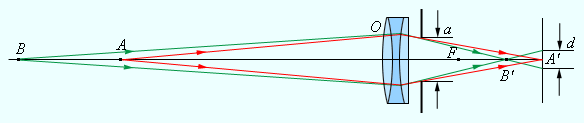Видео:Линза. Формула тонкой линзы. Видеоурок по физике 11 классСкачать Построение изображения в линзах Геометрические построения помогают определить положение изображения, а также его характер. Для этой цели применяют свойства стандартных лучей, направление которых определено. Это лучи, которые проходят через оптический центр либо один из фокусов линзы, и лучи, параллельно расположенные главной либо одной из побочных оптических осей. Рисунки 3 . 3 . 3 и 3 . 3 . 4 демонстрируют данные построения. Рисунок 3 . 3 . 3 . Построение изображения в собирающей линзе. Рисунок 3 . 3 . 4 . Построение изображения в рассеивающей линзе. Стоит выделить то, что стандартные лучи, использованные на рисунках 3 . 3 . 3 и 3 . 3 . 4 для построения изображений, не проходят через линзу. Данные лучи не используются в построении изображения, но могут быть использованы в этом процессе. Для расчета положения изображения и его характера используется формула тонкой линзы. Если записать расстояние от предмета до линзы как d , а от линзы до изображения как f , то формула тонкой линзы имеет вид: 1 d + 1 f + 1 F = D. Величина D – это оптическая сила линзы, равная обратному фокусному расстоянию. Диоптрия ( д п т р ) является единицей измерения оптической силы, фокусное расстояние которой равно 1 м : 1 д п т р = м — 1 . Формула тонкой линзы аналогична формуле сферического зеркала. Можно вывести ее для параксиальных лучей из подобия треугольников на рисунках 3 . 3 . 3 либо 3 . 3 . 4 . Фокусное расстояние линз записывается с определенными знаками: собирающая линза F > 0 , рассеивающая F 0 . Величина d и f тоже подчиняются определенным знакам: d > 0 и f > 0 – применительно к действительным предметам (то есть реальным источникам света) и изображений; d 0 и f 0 – применительно к мнимым источникам и изображениям. 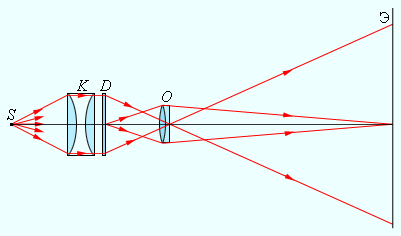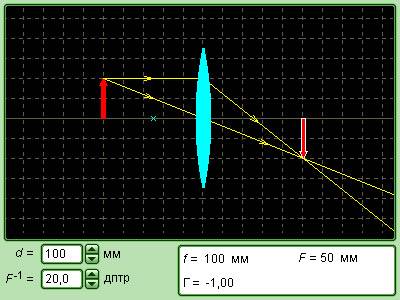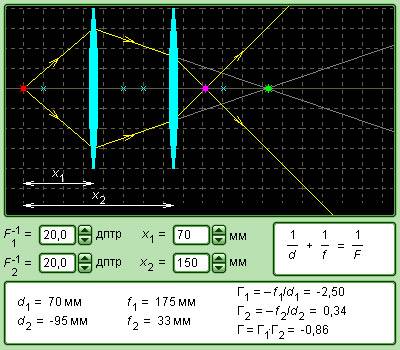Для случая на рисунке 3 . 3 . 3 F > 0 (линза собирающая), d = 3 F > 0 (действительный предмет). Из формулы тонкой линзы получаем: f = 3 2 F > 0 , означает, что изображение действительное. Для случая на рисунке 3 . 3 . 4 F 0 (линза рассеивающая), d = 2 | F | > 0 (действительный предмет), справедлива формула f = — 2 3 F 0 , следовательно, изображение мнимое. Линейные размеры изображения зависят от положения предмета по отношению к линзе. Линейное увеличение линзы Г – это отношение линейных размеров изображения h ‘ и предмета h . Величину h ‘ удобно записывать со знаками плюс или минус, в зависимости от того, прямое оно или перевернутое. Она всегда положительна. Потому для прямых изображений применяется условие Γ > 0 , для перевернутых Γ 0 . Из подобия треугольников на рисунках 3 . 3 . 3 и 3 . 3 . 4 нетрудно вывести формулу для расчета линейного увеличения тонкой линзы: В примере с собирающей линзой на рисунке 3 . 3 . 3 при d = 3 F > 0 , f = 3 2 F > 0 . Значит, Г = — 1 2 0 – изображение перевернутое и уменьшенное в два раза. В примере с рассеивающей линзой на рисунке 3 . 3 . 4 при d = 2 | F | > 0 , справедлива формула f = — 2 3 F 0 ; значит, Г = 1 3 > 0 – изображение прямое и уменьшенное в три раза. Оптическая сила D линзы находится в зависимости от радиусов кривизны R 1 и R 2 , ее сферических поверхностей, а также и от показателя преломления n материала линзы. В теории оптики имеет место следующее выражение: D = 1 F = ( n — 1 ) 1 R 1 + 1 R 2 . Выпуклая поверхность имеет положительный радиус кривизны, а вогнутая поверхность – отрицательным. Данная формула применима в изготовлении линз с заданной оптической силой. Многие оптические приборы устроены таким образом, что свет последовательно проходит через 2 или несколько линз. Изображение предмета от 1 -й линзы служит предметом (действительным или мнимым) для 2 -й линзы, выстраивающей, в свою очередь, 2 -е изображение предмета, которое также может быть действительным либо мнимым. Расчет оптической системы из 2 -х тонких линз состоит в 2 -кратном применении формулы линзы, причем расстояние d 2 от 1 -го изображения до 2 -й линзы следует предложить равное величине l – f 1 , где l – это расстояние между линзами. Вычисленная, по формуле линзы, величина f 2 предопределяет положение 2 -го изображения, а также его характер ( f 2 > 0 – действительное изображение, f 2 0 – мнимое). Общее линейное увеличение Γ системы из 2 -х линз равняется произведению линейных увеличений 2 -х линз, то есть Γ = Γ 1 · Γ 2 . Если предмет либо его изображение находятся в бесконечности, тогда линейное увеличение не имеет смысла. Видео:🔎 Оптика: законы света и линзы с нуля | Физика ЕГЭ 2024 | УмскулСкачать Астрономическая труба Кеплера и земная труба Галилея Рассмотрим частный случай – телескопический ход лучей в системе из 2 -х линз, когда и предмет, и 2 -е изображение расположены на бесконечно больших расстояниях друг от друга. Телескопический ход лучей выполняется в зрительных трубах: земной трубе Галилея и астрономической трубе Кеплера. Тонкая линза имеет некоторые недостатки, которые не позволяют получать изображения высокого разрешения. Аберрация – это искажение, которое возникает в процессе формирования изображения. В зависимости от расстояния, на котором проводится наблюдение, аберрации могут быть сферическими и хроматическими. Смысл сферической аберрации в том, что при широких световых пучках лучи, находящиеся на далеком расстоянии от оптической оси, пересекают ее не в месте фокуса. Формула тонкой линзы действует лишь для лучей, которые находятся близко к оптической оси. Изображение удаленного источника, которое создается широким пучком лучей, преломленных линзой, размыто. Смысл хроматической аберрации в том, что на показатель преломления материала линзы влияет длина световой волны λ . Данное свойство прозрачных сред называют дисперсией. Фокусное расстояние линзы различно для света с различными длинами волн. Данный факт приводит к размытию изображения при излучении немонохроматического света. Современные оптические приборы оснащены не тонкими линзами, а сложными линзовыми системами, в которых есть возможность исключить некоторые искажения. В таких приборах, как фотоаппараты, проекторы и т.д., используются собирающие линзы для формирования действительных изображений предметов. Видео:Урок 210 (осн). Построение изображений с помощью линзСкачать Что представляет собой фотоаппарат Фотоаппарат – это замкнутая светонепроницаемая камера, в которой изображение запечатленных предметов создается на пленке системой линз – объективом. На время экспозиции объектив открывается и закрывается с помощью специального затвора. Особенность работы фотоаппарата в том, что на плоской фотопленке получаются довольно резкие изображения предметов, которые находятся на различных расстояниях. Резкость меняется вследствие перемещения объектива относительно фотопленки. Изображения точек, которые не лежат в плоскости резкого наведения, выходят на снимках размытыми в виде рассеянных кружков. Размер d данных кружков можно уменьшить методом диафрагмирования объектива, то есть уменьшения относительного отверстия a F , как показано на рисунке 3 . 3 . 5 . Это в результате увеличивает глубину резкости. Рисунок 3 . 3 . 5 . Фотоаппарат. С помощью проекционного аппарата удается снять масштабные изображения. Объектив O проектора фокусирует изображение плоского предмета (диапозитив D ) на удаленном экране Э (рисунок 3 . 3 . 6 ). Система линз K (конденсор) используется для концентрации света источника S на диапозитиве. На экране воссоздается увеличенное перевернутое изображение. Масштаб проекционного устройства можно изменять, приближая или отдаляя экран и одновременно изменяя расстояние между диапозитивом D и объективом O . Рисунок 3 . 3 . 6 . Проекционный аппарат. Рисунок 3 . 3 . 7 . Модель тонкой линзы. Рисунок 3 . 3 . 8 . Модель системы из двух линз. 💡 Видео Физика. Геометрическая оптика: Тонкие линзы. Центр онлайн-обучения «Фоксфорд»Скачать § 68-69. Линзы. Изображения, даваемые линзой.Скачать Как найти построением положение фокусов линзыСкачать 11 класс, 12 урок, Построение изображений в линзахСкачать ОЛИМПИАДНАЯ ФИЗИКА. Геометрическая оптика - 1Скачать 🔴 Курс ОГЭ-2024 по физике. Урок №29. Линзы. Глаз как оптическая система | Бегунов М.И.Скачать 87. Геометрическая оптикаСкачать Поделиться или сохранить к себе: Смотрите также 2 параллельные прямые пересекаются 3 прямой найди углы сумма которых данным углом равна 180 градусов 2 параллельные прямые пересечены 3 прямой то внутренние накрест лежащие углы равны 2 прямые параллельны одной и той же плоскости можно ли утверждать что эти прямые Четырехугольник у которого противолежащие стороны параллельны то есть лежат на параллельных прямых 1 вписанный угол опирающийся на полуокружность острый 2 если две параллельные прямые пересечены 1 даны 2 параллельные прямые и секущая построить окружность касающуюся всех 3 х прямых 1 из внутренних односторонних углов образованных при пересечении 2 параллельных прямых 3 прямой 1 из односторонних углов образованных при пересечении 2 параллельных прямых секущей в 4 раза больше