Прямая имеет две общие точки с окружностью с центром

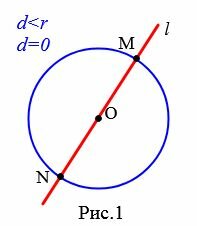
Выясним количество общих точек прямой и окружности в зависимости от их взаимного расположения. Если прямая l проходит через центр O окружности (Рис.1), то она пересекает окружность в двух точках, которые являются концами диаметра окружности.

Пусть прямая не проходит через центр окружности. Проведем перпендикуляр OH к прямой l (Рис.2, Рис.3, Рис.4). Обозначим расстояние от центра окружности до прямой l буквой d. Рассмотрим сколько общих точек будут иметь прямая и окружность в зависимости от соотношения d и r.

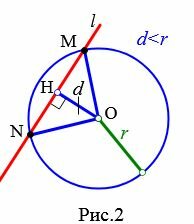Теорема 1. Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.

В этом случае прямая называется секущей по отношению к окружности.

Доказательство. Пусть расстояние от центра окружности до прямой меньше радиуса окружности: d Теорема 2. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку.

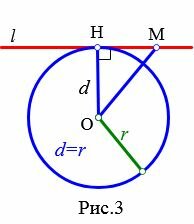Доказательство. Пусть расстояние от центра окружности до прямой равно радиусу окружности: d=r (Рис.3). В этом случае OH=r, т.е. точка H лежит на окружности и является общей точкой прямой l и окружности. Возьмем на прямой l любую точку M отличной от H. Тогда расстояние от OM больше расстояния OH=r, поскольку наклонная OM больше перпендикуляра OH к прямой l. Следовательно точка M не лежит на окружности. Получили, что точка H единственная общая точка прямой l и окружности.

Теорема 3. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.

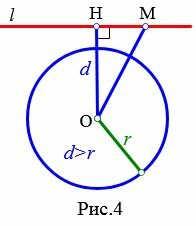Доказательство. Пусть расстояние от центра окружности до прямой больше радиуса окружности:d>r (Рис.4). Тогда ( small OH > r). Возьмем на прямой l любую точку M отличной от H. Тогда ( small OM > OH>r). Следовательно точка M не лежит на окружности. Таким образом, если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.

Видео:ОГЭ Задание 25 Две окружностиСкачать

Уравнение окружности x2 + y2 = 100 Уравнение прямой y = b?

Математика | 5 — 9 классы

Уравнение окружности x2 + y2 = 100 Уравнение прямой y = b.

Найди значения b, с которыми.

(запиши ответы, используя необходимые знаки = , &lt ; , &gt ; , слова и, или и числовые значения b, соблюдая направление числовой оси слева направо).

1. . прямая имеет одну общую точку с окружностью b b 2.

. прямая имеет две общие точки с окружностью b b 3.

. прямая не имеет общих точек с окружностью b b.

Это окружность с центром в начале координат ; r = кор(100) = 10 ;

1) для 1 общей точки эта прямая должна быть касательной, в данном случае должна равнятся радиусу окружности, значит b = 10 ; y = 10 ; или b = — 10 ; y = — 10, тоже правильно

Е b&lt ; 10, но это окружность, значит : — 10&lt ; b&lt ; 10 ; или b = ( — 10 ; 10)

3) для этого b&gt ; r, значит b&gt ; 10 и b&lt ; — 10 ; или

b = ( — беск ; — 10) и (10 ; + беск).

Видео:Прямая и окружность. Математика. 6 класс.Скачать

С объяснением?

На окружности отмечено 2017 различных точек А1, …, А2017 и проведены все возможные хорды, попарно соединяющие эти точки.

Через точку А1 проведена прямая, не проходящая ни через одну из точек А2, … А2017.

Найдите наибольшее возможное количество хорд, которые могут иметь хотя бы одну общую точку с этой прямой.

Видео:Окружность и прямая: варианты взаимного расположенияСкачать

Начертите окружность с радиусом 3 см?

Начертите окружность с радиусом 3 см.

1)Проведите прямую а, имеющую с окружностью только одну точку.

Каково взаимное расположение прямой а и окружности?

2)Проведите прямую b, имеющую с окружностью две общие точки.

Каково взаимное расположение прямой b и окружности?

Видео:Теорема о числе точек пересечения двух окружностейСкачать

Постройте график функции и определите, при каких значениях прямая м имеет с графиком ровно одну общую точку?

Постройте график функции и определите, при каких значениях прямая м имеет с графиком ровно одну общую точку.

Видео:Уравнение окружности (1)Скачать

На диаметре AB окружности выбрали точку C не совпадающие с точками A и B сколько общих точек с окружностью имеет Луч вершина которого совпадает с точкой C?

На диаметре AB окружности выбрали точку C не совпадающие с точками A и B сколько общих точек с окружностью имеет Луч вершина которого совпадает с точкой C?

1) ни одной , 2) одну , 3) две , 4) три ?

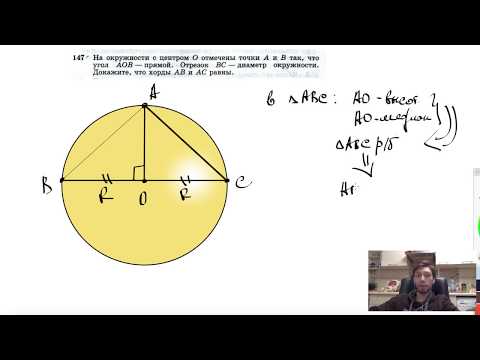
Видео:№147. На окружности с центром О отмечены точки А и В так, что угол АОВ — прямой. Отрезок ВССкачать

Радиус окружности равен 6 центр окружности принадлежит оси Ох и имеет положительную абциссу окружность проходит через точку (5 ; 0)напишите уравнение окружности?

Радиус окружности равен 6 центр окружности принадлежит оси Ох и имеет положительную абциссу окружность проходит через точку (5 ; 0)напишите уравнение окружности.

Видео:Геометрия. ОГЭ по математике. Задание 16Скачать

Начерти окружность и отрезок так чтобы отрезок имел с окружностью первом варианте одну общую точку Во втором варианте только две общие точки?

Начерти окружность и отрезок так чтобы отрезок имел с окружностью первом варианте одну общую точку Во втором варианте только две общие точки.

Видео:Геометрия 8 класс (Урок№25 - Взаимное расположение прямой и окружности.)Скачать

Помогите пожалуйста 1?

Помогите пожалуйста 1.

Написать общее уравнение прямой, если прямая проходит через точку A(8 ; — 4) и имеет направляющий вектор a(4 ; 1).

2. Написать общее уравнение прямой, если прямая проходит через точку N( — 2 ; 6) и имеет угловой коэффициент k = 2.

3. Написать общее уравнение прямой, если прямая проходит через точки K(4 ; 3) и B(5 ; 2).

4. Написать общее уравнение прямой, если прямая проходит через точку M( — 2 ; 4) и имеет нормальный вектор n(6 ; 2).

5. Определить координаты направляющего вектора прямой x — 1 / 12 = y + 2 / — 4.

6. Найти угловой коэффициент прямой 6x + 3y — 13 = 0.

Видео:Найти центр и радиус окружностиСкачать

Сколько общих точек имеет прямая и окружность, диаметр которой равен 8см, если прямая расположена на расстоянии 5см от центра окружности?

Сколько общих точек имеет прямая и окружность, диаметр которой равен 8см, если прямая расположена на расстоянии 5см от центра окружности?

Видео:🔴 В окружности с центром O отрезки AC и BD ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Начертите окружность радиусом 1, 5 см и отметьте на ней точку Б?

Начертите окружность радиусом 1, 5 см и отметьте на ней точку Б.

Через эту точку проведите такую прямую, чтобы у данной прямой и окружности не было общих точек.

Начертите окружность диаметром 4 см и вне окружности отметьте точку К.

От этой точки проведите к окружности прямую так, чтобы она касалась окружности.

Сколько таких прямых можно провести?

Помогите пожалуйста срочно!

Видео:Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Найдите все значения k при каждом из которых прямая y = kx имеет с графиком функции y = — 3x ^ 2 — 3 ровно одну общую точку?

Найдите все значения k при каждом из которых прямая y = kx имеет с графиком функции y = — 3x ^ 2 — 3 ровно одну общую точку.

Постройте этот график и прямые : ).

Вы перешли к вопросу Уравнение окружности x2 + y2 = 100 Уравнение прямой y = b?. Он относится к категории Математика, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Математика. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

Видео:На окружности с центром O отмечены точки A и B так ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Касательная к окружности

О чем эта статья:

Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Видео:2023 На окружности с центром в точке О отмечены точки А и Б так что угол аоб равен 45Скачать

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

• окружность с центральной точкой А;
• прямая а — касательная к ней;
• радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°

Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.

Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.

Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.

Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.

∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).

Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ — ВС = 16 — 12 = 4 (см)

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

(у + R) 2 : 4 = (у + R) × (у — R)

Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Ответ: MO = 10 см.

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.

АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°

📺 Видео

Окружность и круг, 6 классСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Быстро и легко определяем центр любой окружностиСкачать