Прямая ас проходит через центр окружности точку а

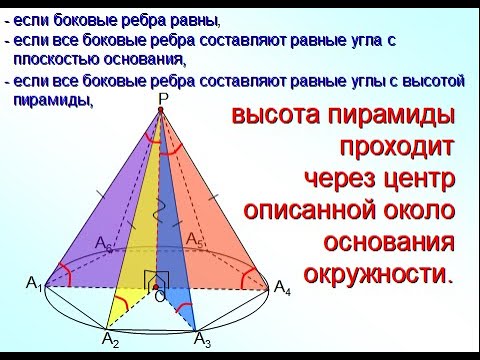
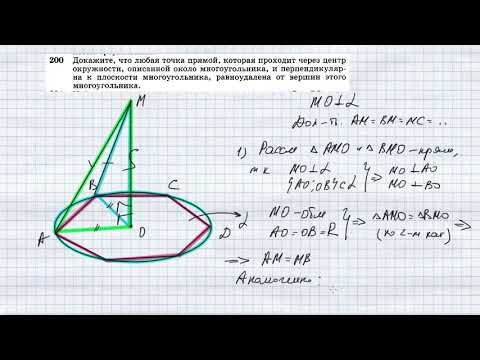
Видео:№200. Докажите, что любая точка прямой, которая проходит через центр окружности, описанной около мноСкачать

Ваш ответ

Видео:№204. Прямая ОМ перпендикулярна к плоскости правильного треугольника ABC и проходит через центр ОСкачать

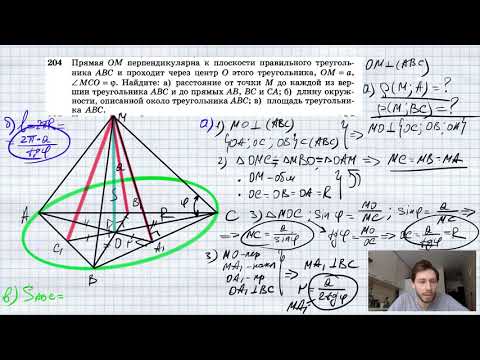
решение вопроса

Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 606,997
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Окружность с центром на стороне AС треугольника ABC проходит через вершину С и касается прямой AB вСкачать

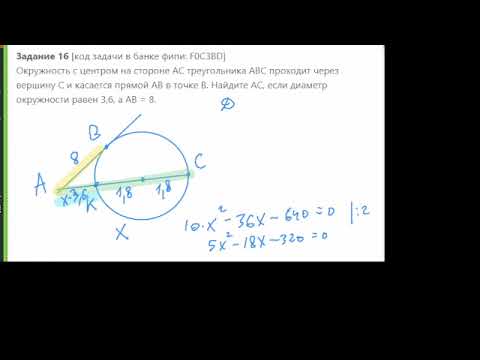
Прямая ас проходит через центр окружности точку а

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 7,5, а AB = 2.

Пусть О — центр окружности. Радиус окружности, проведённый в точку касания, перпендикулярен касательной. Поэтому треугольник OBA — прямоугольный. Найдём OA по теореме Пифагора:

Следовательно, длина стороны AC равна

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 8, а AB = 3.

Пусть О — центр окружности. Радиус окружности, проведённый в точку касания, перпендикулярен касательной. Поэтому треугольник OBA — прямоугольный. Найдём OA по теореме Пифагора:

Следовательно, длина стороны AC равна

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 8,4, а AB = 4.

Пусть О — центр окружности. Радиус окружности, проведённый в точку касания, перпендикулярен касательной. Поэтому треугольник OBA — прямоугольный. Найдём OA по теореме Пифагора:

Следовательно, длина стороны AC равна

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB = 1, AC = 5.

Проведём радиус Пусть R — длина радиуса окружности. Заметим, что Поскольку OB — радиус, проведённый в точку касания Рассмотрим прямоугольный треугольник AOB, по теорем Пифагора:

Таким образом, диаметр окружности равен 4,8.

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 3, 6, а AB = 8.

Пусть О — центр окружности. Радиус окружности, проведённый в точку касания, перпендикулярен касательной. Поэтому треугольник OBA — прямоугольный. Найдём OA по теореме Пифагора:

Следовательно, длина стороны AC равна

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB = 3, AC = 5.

Проведём радиус Пусть R — длина радиуса окружности. Заметим, что Поскольку OB — радиус, проведённый в точку касания Рассмотрим прямоугольный треугольник AOB, по теореме Пифагора:

Таким образом, диаметр окружности равен 3,2.

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB = 9, AC = 12.

Пусть окружность второй раз пересекает прямую AC в точке D, а DC = x . Тогда по свойству касательной и секущей, проведённых из одной точки к окружности, получаем

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 16, а AB = 15.

Это задание ещё не решено, приводим решение прототипа.

Окружность с центром на стороне A C треугольника A B C проходит через вершину C и касается прямой A B в точке B . Найдите A C , если диаметр окружности равен 7,5, а A B = 2 .

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB = 4, AC = 10.

Это задание ещё не решено, приводим решение прототипа.

Окружность с центром на стороне A C треугольника A B C проходит через вершину C и касается прямой A B в точке B . Найдите A C , если диаметр окружности равен 7,5, а A B = 2 .

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 4,8, а AB = 1.

Это задание ещё не решено, приводим решение прототипа.

Окружность с центром на стороне A C треугольника A B C проходит через вершину C и касается прямой A B в точке B . Найдите A C , если диаметр окружности равен 7,5, а A B = 2 .

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB = 15, AC = 25.

Это задание ещё не решено, приводим решение прототипа.

Окружность с центром на стороне A C треугольника A B C проходит через вершину C и касается прямой A B в точке B . Найдите A C , если диаметр окружности равен 7,5, а A B = 2 .

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB = 8, AC = 10.

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB = 4, AC = 16.

Это задание ещё не решено, приводим решение прототипа.

Окружность с центром на стороне A C треугольника A B C проходит через вершину C и касается прямой A B в точке B . Найдите A C , если диаметр окружности равен 7,5, а A B = 2 .

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB = 2, AC = 8.

Это задание ещё не решено, приводим решение прототипа.

Окружность с центром на стороне A C треугольника A B C проходит через вершину C и касается прямой A B в точке B . Найдите A C , если диаметр окружности равен 7,5, а A B = 2 .

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB = 3, AC = 9.

Это задание ещё не решено, приводим решение прототипа.

Окружность с центром на стороне A C треугольника A B C проходит через вершину C и касается прямой A B в точке B . Найдите A C , если диаметр окружности равен 7,5, а A B = 2 .

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB = 9, AC = 12.

Это задание ещё не решено, приводим решение прототипа.

Окружность с центром на стороне A C треугольника A B C проходит через вершину C и касается прямой A B в точке B . Найдите A C , если диаметр окружности равен 7,5, а A B = 2 .

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 15, а AB = 4.

Это задание ещё не решено, приводим решение прототипа.

Окружность с центром на стороне A C треугольника A B C проходит через вершину C и касается прямой A B в точке B . Найдите A C , если диаметр окружности равен 7,5, а A B = 2 .

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 5,25, а AB = 9.

Это задание ещё не решено, приводим решение прототипа.

Окружность с центром на стороне A C треугольника A B C проходит через вершину C и касается прямой A B в точке B . Найдите A C , если диаметр окружности равен 7,5, а A B = 2 .

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB = 6, AC = 10.

Это задание ещё не решено, приводим решение прототипа.

Окружность с центром на стороне A C треугольника A B C проходит через вершину C и касается прямой A B в точке B . Найдите A C , если диаметр окружности равен 7,5, а A B = 2 .

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 6,4, а AB = 6.

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 3,2, AB = 3.

Это задание ещё не решено, приводим решение прототипа.

Окружность с центром на стороне A C треугольника A B C проходит через вершину C и касается прямой A B в точке B . Найдите A C , если диаметр окружности равен 7,5, а A B = 2 .

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 6,4, а AB = 6.

Это задание ещё не решено, приводим решение прототипа.

Окружность с центром на стороне A C треугольника A B C проходит через вершину C и касается прямой A B в точке B . Найдите A C , если диаметр окружности равен 7,5, а A B = 2 .

Окружность с центром на стороне треугольника проходит через вершину и касается прямой в точке . Найдите , если диаметр окружности равен 6,4, а .

Окружность с центром на стороне треугольника проходит через вершину и касается прямой в точке . Найдите диаметр окружности, если , .

Видео:Задание 24 ОГЭ по математике #2Скачать

Касательная к окружности

О чем эта статья:

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Видео:Пирамиды, в которых высота проходит через центр описанной около основания окружностиСкачать

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

• окружность с центральной точкой А;
• прямая а — касательная к ней;
• радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°

Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.

Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.

Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.

Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.

∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).

Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ — ВС = 16 — 12 = 4 (см)

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

(у + R) 2 : 4 = (у + R) × (у — R)

Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Ответ: MO = 10 см.

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.

АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°

🌟 Видео

Урок 3. №23 ОГЭ. Касательная. Окружность с центром на стороне AC касается АВ в точке В.Скачать

Математика ОГЭ. Задача 26_4Скачать

ОГЭ. Задание 24. Геометрическая задача на вычислениеСкачать

ЕГЭ задание 16 Внутреннее касание двух окружностейСкачать

Через точку A, лежащую вне окружности, проведены две прямые.Скачать

№147. На окружности с центром О отмечены точки А и В так, что угол АОВ — прямой. Отрезок ВССкачать

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

2020 точка О центр окружности на которой лежат точки A B и C известно что Угол ABC равен 62 градусаСкачать

2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

Геометрия Две окружности касаются внутренним образом в точке A, причем меньшая окружность проходитСкачать

Геометрия В треугольнике ABC известны длины сторон AB = 18, AC = 36, точка O — центр окружностиСкачать

№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать

ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать