- «Календарь счастливой жизни: инструменты и механизм работы для достижения своих целей»
- На рисунке 88, б прямые а и b пересекают стороны треугольника ABC так, что угол 5 = углу 6, а угол 7 = углу 8. а) Докажите, что прямые а и АС параллельны. б) Верно ли, что b || АВ?
- Ваш ответ
- решение вопроса
- Похожие вопросы
- Геометрия. 7 класс
- 📺 Видео
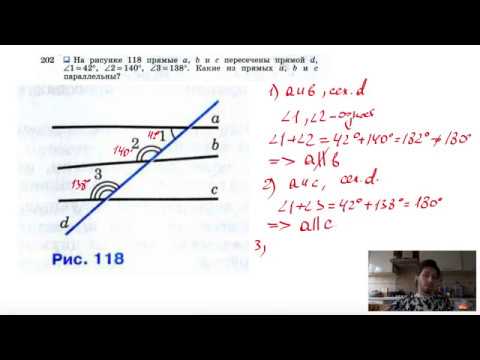
Видео:№202. На рисунке 116 прямые а, b и с пересечены прямой d, ∠1=42°, ∠2=140°, ∠3=138°. Какие из прямыхСкачать
«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику
Задание 1 На рисунке изображены прямые а , в и секущая с . Какое условие должно выполняться, чтобы прямые а и в были параллельны (рис №1).
Задание 2 Выберите верные утверждения.
1) Через любую точку на плоскости проходят две прямые параллельные данной прямой.
2) Две непересекающиеся прямые параллельны.
3) Если при пересечении двух прямых секущей односторонние углы равны, то прямые параллельны.
4) Две прямые перпендикулярные третьей параллельны.
5) Если при пересечении двух прямых смежные углы составляют 180°, то прямые параллельны.
Задание 3 Прямые l и f параллельны, m и n – секущие (рис №2).
Выберите неверные утверждения.
Задание 4 Выберите неверное утверждение.
1) Если две прямые на плоскости не имеют общих точек, то они параллельны.
2) Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
3) Через точку, не лежащую на данной прямой проходит только одна прямая, параллельная данной.
4) Если две прямые параллельны третьей прямой, то они параллельны между собой.
5) Если две параллельные прямые пересечены секущей, то односторонние углы равны.
Задание 5 Данное утверждение «Если две параллельные прямые пересечены секущей, то соответственные углы равны» является:
1) Третьим свойством параллельных прямых.
2) Первым признаком параллельных прямых.
3) Первым свойством параллельных прямых.
4) Вторым признаком параллельных прямых.
5) Вторым свойством параллельных прямых.
Задание 6 Прямые а║в, c ║ d (рис №3) . Какое равенство является неверным.
Задание 7 Если прямые r и x параллельны (рис №4), то неверно …
Задание 8 Аксиома параллельных прямых – это аксиома …
1)Архимеда. 2) Евклида. 3) Лобачевского. 4) Атанасяна. 5) Пифагора.
Задание 9 Теорема « Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны» является для теоремы « Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны» ….
4) Обратной теоремой.
Задание 10 В теореме « Если две прямые параллельны третьей прямой, то они параллельны между собой», различают две части, которые называются:
1) Условие и заключение.
2) Начало и конец.
3) Первая часть и вторая часть.
4) Достаточное и необходимое условия.
5) Прямая и обратная части.
Задание 11 Рисунок соответствует (рисунок №5.1)….
1) Признаку параллельности прямых через соответственные углы.
2) Свойству параллельных прямых через накрест лежащие углы.
3) Следствию, о том, что прямая, пересекающая одну
из параллельных прямых, пересекает и другую.
4) Аксиоме, что через точку, не лежащую на данной прямой проходит только одна прямая, параллельная данной.
5) Свойству параллельных прямых через соответственные углы.
Задание 12 Пятый постулат Евклида формулируется так…
1) Две различные прямые имеют не более одной общей точки.
2) Через точку, не лежащую на данной прямой, проходят две прямые параллельные данной.
3) Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и к другой.
4) Через точку, не лежащую на данной прямой, проходит только одна прямая параллельная данной.
5) Две прямые перпендикулярные к третьей, параллельны.
Задание 13 При доказательстве следствий из аксиомы о параллельных прямых используют метод …
1) от простого к сложному
2) от противного
4) проб и ошибок
Задание 14 Для построения параллельных прямых на практике не используют:
3) линейка и угольник
5) линейка и циркуль.
Задание 15 Какой теореме соответствует данное доказательство (рис №6).
«Углы 2 и 3 вертикальные, тогда они равны по свойству вертикальных углов. Значит по условию, по решению, то. Но углы 1 и 2 накрест лежащие при пресечении прямых m и n секущей с, тогда по первому признаку параллельных прямых m ║ n . ч.т.д.»
1) Свойство накрест лежащих углов, образованных при пересечении параллельных прямых секущей.
2) Признак параллельности прямых через накрест лежащие углы.
3) Признак параллельности прямых через соответственные углы.
4) Свойство соответственных углов, образованных при пересечении параллельных прямых секущей.
5) Признак параллельности прямых через односторонние углы.
Задание 16 При пересечении двух параллельных прямых секущей один из образованных углов на рисунке равен 49°. Найдите углы (рис №7)
Задание 17 Продолжите предложение, чтобы оно стало верным утверждением : « Если прямая перпендикулярна к одной из двух параллельных прямых, то …»
1) они все пересекутся в одной точке;
2) они все параллельны;
3) она параллельна к другой;
4) она перпендикулярна и к другой;
5) она пересекает другую.
Задание 18 Если прямые r и x параллельны, . Найдите градусные меры углов (рис №4)
Задание 19 Укажите теорему, которая имеет условие «при пересечении двух прямых секущей односторонние углы в сумме составляют 180°» , заключение – «прямые параллельны».
1) Если при пересечении двух прямых секущей односторонние углы в сумме составляют 180°, то прямые не параллельны.
2) Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
3) Если при пересечении двух прямых секущей односторонние углы в сумме составляют 180°, то прямые параллельны.
4) Если две прямые пересечены секущей, то сумма односторонних углов равна 180°.
5) Если две параллельные прямые пересечены секущей, то сумма односторонних углов не равна 180°.
Задание 20 Укажите обратную теорему к данной теореме: « Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны».
1) Если параллельные прямые пересечены секущей, то соответственные углы равны.
2) Если при пересечении двух прямых секущей соответственные углы не равны, то прямые не параллельны.
3) Если не параллельные прямые пересечены секущей, то соответственные углы не равны.
4) Для данной теоремы нет обратной.
5) Если две прямые пересечены секущей, то соответственные углы равны.
Задание 21 На каком из пяти рисунков (рисунок №8.1) прямые m и n параллельны по признаку: « Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны».
Задание 22 К какой теореме относится это доказательство, дополните его, чтобы рассуждения были верными (рисунок №10.1).
Известно, что прямые а║в пересечены секущей с. Докажем, что углы 1 и 2 равны.
На рисунке углы 1 и 3 –______________, значит они равны. Углы 2 и 3 накрест лежащие углы при пересечении прямых а║в секущей с, тогда они равны по ____________. Если . Ч.т.д.
1) Первое свойство параллельных прямых; соответственные углы; по 2 свойству параллельных прямых
2) Второй признак параллельных прямых; вертикальные углы; по 1 свойству параллельных прямых.
3). Второе свойство параллельных прямых; вертикальные углы; по 1 свойству параллельных прямых.
4) Первый признак параллельных прямых; соответственные углы; по 1 признаку параллельных прямых.
5) Второе свойство параллельных прямых; вертикальные углы; по 1 признаку параллельных прямых.
Задание 23 Заполните пропуски в формулировке теоремы
Если стороны одного угла __________________________параллельны __________________________другого угла, то
Задание 24 Найдите градусные меры углов 1 и 2 (рис №9), если , а
Впишите ответы в таблицу, по номерам кроме 23 задания.
Количество верных ответов ______________________
Задание 1 На рисунке изображены прямые а , в и секущая с . Какое условие должно выполняться, чтобы прямые а и в были параллельны (рис №1).
Задание 2 Выберите верные утверждения.
1) Если при пересечении двух прямых секущей вертикальные углы равны, то прямые параллельны. Если
2) Две прямые параллельные третьей перпендикулярны..
3) Если две прямые не пересекаются, то они параллельны.
4) прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.
5) Любые две прямые на плоскости параллельны.
Задание 3 Прямые l и f параллельны, m и n – секущие (рис№2). Выберите верные утверждения.
Задание 4 Выберите неверное утверждение.
1) Если две прямые на плоскости не имеют общих точек, то они параллельны.
2) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
3)Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны..
4) Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.
5) Через точку, не лежащую на данной прямой проходят прямые, параллельные данной.
Задание 5 Данное утверждение «Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны» является:
1) Первым признаком параллельных прямых
2) Первым свойством параллельных прямых
3) Вторым свойством параллельных прямых.
4) Вторым признаком параллельных прямых.
5) Третьим свойством параллельных прямых.
Задание 6 Прямые а║в, c ║ d (рис №3) . Какое равенство является неверным.
Задание 7 Если прямые r и x параллельны (рис №4), то неверно …
Задание 8 Аксиома параллельных прямых – это аксиома …
1) Инков 2) Пифагора 3) Ломоносова 4) Народная. 5) Евклида. .
Задание 9 Теорема « Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°» является для теоремы « Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны» ….
2) Прямой теоремой.
3) Обратной теоремой.
Задание 10 В теореме « Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны» различают две части, которые называются:
1) Условие и заключение.
2) Начало и конец.
3) Первая часть и вторая часть.
4) Достаточное и необходимое условия.
5) Прямая и обратная части.
Задание 11 Рисунок соответствует доказательству (рисунок №5.2)….
1) Аксиоме, что через точку, не лежащую на данной прямой проходит только одна прямая, параллельная данной.
2) Свойства параллельных прямых через накрест лежащие углы.
3) Признака параллельности прямых через соответственные углы.
4) Следствия, о том, что если две прямые параллельны третьей прямой, то они параллельны.
5) Свойства параллельных прямых через соответственные углы.
Задание 12 Определение параллельных прямых формулируется так…
1) Две прямые на плоскости называются параллельными, если они не пересекаются.
2) Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
3) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
4) Две прямые перпендикулярные к третьей, параллельны
5) Если две прямые перпендикулярны третьей прямой, то они параллельны.
Задание 13 При доказательстве свойства параллельных прямых через накрест лежащие углы использую метод …
3) проб и ошибок
4) от простого к сложному
5) от противного
Задание 14 Для построения параллельных прямых на практике не используются:
3) линейка и угольник
5) линейка и циркуль.
Задание 15 Какой теореме соответствует данное доказательство (рисунок №6.2).
«Углы 2 и 4 смежные , тогда их сумма равна 180° по свойству смежных углов. Значит по условию, по решению, то. Но углы 1 и 2 накрест лежащие при пресечении прямых m и n секущей с, тогда по первому признаку параллельных прямых m ║ n . ч.т.д.»
1) Признак параллельности прямых через соответственные углы.
2) Признак параллельности прямых через накрест лежащие углы.
3) Свойство односторонних углов, образованных при пересечении параллельных прямых секущей.
4) Свойство соответственных углов, образованных при пересечении параллельных прямых секущей.
5) Признак параллельности прямых через односторонние углы.
Задание 16 При пересечении двух параллельных прямых секущей один из образованных углов на рисунке равен 106°. Найдите углы
Задание 17 Продолжите предложение, чтобы оно стало верным утверждением : « Если две прямые параллельны третьей прямой, то …»
1) они все параллельны;
2) они перпендикулярны;
3) они все пересекутся в одной точке;
4) они образуют прямоугольник;
5) соответственные углы равны
Задание 18 Если прямые r и x параллельны, . Найдите градусные меры углов (рис №4)
Задание 19 Укажите теорему, которая имеет условие
«при пересечении двух прямых секущей соответственные углы равны » , заключение – «прямые параллельны».
1) Если при пересечении двух прямых секущей соответственные углы равны, то прямые не параллельны
2) Если две параллельные прямые пересечены секущей, то соответственные углы равны.
3). Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
4) Если две прямые пересечены секущей, то соответственные углы равны.
5) Если две параллельные прямые пересечены секущей, то соответственные углы не равны.
Задание 20 Укажите теорему, которая является обратной для теоремы с условием « две параллельные прямые пересечены секущей» и заключением «накрест лежащие углы равны».
1) Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
2) Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
3) Если две прямые пересечены секущей, то накрест лежащие углы не равны.
4) Если накрест лежащие углы при пересечении двух прямых секущей не равны, то прямые не параллельны.
5) Недостаточно данных.
Задание 21 На каком из пяти рисунков (рисунок №8.2) прямые m и n параллельны по признаку: « Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны».
Задание 22 К какой теореме относится это доказательство, дополните его, чтобы рассуждения были верными (рисунок №10.2).
Известно, что прямые а║в пересечены секущей с. Докажем, что сумма углов 1 и 2 равна 180°.
На рисунке углы 1 и 3 –______________, значит они в сумме равны 180°. Углы 2 и 3 накрест лежащие углы при пересечении прямых а║в секущей с, тогда они равны по ____________. Если . Ч.т.д.
1) Третье свойство параллельных прямых; смежные углы; по 1 признаку параллельных прямых
2) Третий признак параллельных прямых; смежные углы; по 1 свойству параллельных прямых.
3). Третье свойство параллельных прямых; смежные углы; по 1 свойству параллельных прямых.
4) Первый признак параллельных прямых; односторонние углы; по 1 признаку параллельных прямых.
5) Второе свойство параллельных прямых; вертикальные углы; по 1 признаку параллельных прямых.
Задание 23 Заполните пропуски в формулировке следствия
Если прямая перпендикулярна к одной из двух ___________________________________прямых, то она __________
Задание 24 Найдите градусные меры углов 1 и 2 (рисунок №9), если , а
Впишите ответы в таблицу, по номерам кроме 23 задания.
Количество верных ответов ______________________
Задание 1 На рисунке изображены прямые а , в и секущая с . Какое условие должно выполняться, чтобы прямые а и в были параллельны (рисунок №1).
Задание 2 Выберите верные утверждения.
1) Если при пересечении двух прямых секущей односторонние углы равны, то прямые параллельны
2) Если при пересечении двух параллельных прямых секущей один из соответственных углов равен 70°, то другой 110°..
3). Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
4) Если прямая пересекает одну из параллельных прямых, то она пересечет и другую.
5) Если при пересечении двух прямых вертикальные углы равны, то прямые параллельны.
Задание 3 Прямые l и f параллельны, m и n – секущие (рисунок №2). Выберите неверные утверждения.
Задание 4 Выберите неверное утверждение.
1) Через точку, не лежащую на данной прямой проходит только одна прямая, параллельная данной.
2) Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
3) Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
4) Если при пересечении двух прямых секущей соответственные углы составляют 180°, то прямые параллельны
5) Если две прямые параллельны третьей прямой, то они параллельны между собой.
Задание 5 Данное утверждение «Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180° » является:
1) Третьим признаком параллельных прямых.
2) Вторым свойством параллельных прямых.
3) Третьим свойством параллельных прямых.
4) Первым свойством параллельных прямых.
5) Вторым признаком параллельных прямых.
Задание 6 Прямые а║в, c ║ d (рисунок №3) . Какое равенство является неверным.
Задание 7 Если прямые r и x параллельны (рисунок №4), то неверно …
Задание 8 Аксиома параллельных прямых – это аксиома …
1). Архимеда 2) Евклида. 3) Атанасяна. 4) Магницкого. 5) Пифагора.
Задание 9 Теорема « Если две параллельные прямые пересечены секущей, то соответственные углы равны» является для теоремы « Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны» ….
1) Прямой теоремой.
5) Обратной теоремой.
Задание 10 В теореме « Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны», различают две части, которые называются:
1). Первая часть и вторая часть.
2) Начало и конец.
3) Условие и заключение
4) Достаточное и необходимое условия.
5) Прямая и обратная части.
Задание 11 Рисунок соответствует доказательству (рис №5.1)….
1) Свойства вертикальных углов.
2) Следствия из свойства параллельных прямых через накрест лежащие углы.
3) Признака параллельности прямых через односторонние
4) Следствия, о том, что прямая, пересекающая одну из параллельных прямых, пересекает и другую.
5) Признака параллельности прямых через соответственные углы.
Задание 12 Аксиома параллельных прямых формулируется так…
1) Через любые две точки проходит прямая, и притом только одна.
2) Если две прямые перпендикулярны третьей прямой, то они параллельны.
3) Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и к другой.
4) Через точку, не лежащую на данной прямой, проходит только одна прямая параллельная данной.
5) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Задание 13 При доказательстве следствий из аксиомы о параллельных прямых используют метод
1) от противного
2) практических исследований
3) математической индукции
Задание 14 . Для построения параллельных прямых на практике не используют:
3) линейка и угольник
5) линейка и циркуль.
Задание 15 Какой теореме соответствует данное доказательство (рис №6.3).
« Так как прямые m ║ n , то накрест лежащие углы 1 и 3 равны по первому свойству параллельных прямых. Углы 2 и 3 вертикальные, тогда они равны по свойству вертикальных углов. Значит , , тогда. ч.т.д.»
1) Свойство накрест лежащих углов, образованных при пересечении параллельных прямых секущей.
2) Признак параллельности прямых через накрест лежащие углы.
3) Свойство соответственных углов, образованных при пересечении параллельных прямых секущей.
4) Признак параллельности прямых через соответственные углы.
5) Признак параллельности прямых через односторонние углы.
Задание 16 При пересечении двух параллельных прямых секущей один из образованных углов на рисунке равен 49°. Найдите углы (рис №7)
Задание 17 Продолжите предложение, чтобы оно стало верным утверждением : « Если при пересечении двух прямых секущей соответственные углы равны, то …»
1) такой теоремы нет.;
2) односторонние углы равны;
3) секущая перпендикулярна этим прямым;
4) прямые пересекутся в одной точке;
5) прямые параллельны
Задание 18 Если прямые r и x параллельны, . Найдите градусные меры углов (рис №4)
Задание 19 Укажите теорему, которая имеет условие «при пересечении двух прямых секущей накрест лежащие углы равны» , заключение – «прямые параллельны».
1) Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые не параллельны
2) Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
3). Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
4) Если две прямые пересечены секущей, то накрест лежащие углы равны.
5) Если две параллельные прямые пересечены секущей, то накрест лежащие углы не равны.
Задание 20 Укажите обратную теорему к данной теореме: « Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны».
1) Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
2) Если при пересечении двух прямых секущей накрест лежащие углы не равны, то прямые не параллельны.
3) Если не параллельные прямые пересечены секущей, то накрест лежащие углы не равны.
4) Если две прямые пересечены секущей, то накрест лежащие углы равны.
5) Для данной теоремы нет обратной
Задание 21 На каком из пяти рисунков (рисунок №8.3) прямые m и n параллельны по признаку: « Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны».
Задание 22 К какой теореме относится это доказательство, дополните его, чтобы рассуждения были верными (рис №10.3).
Известно, что прямые а║в пересечены секущей с. Докажем, что углы 1 и 2 __________ .
На рисунке углы 1 и 3 –______________, значит они равны. Углы 2 и 3 накрест лежащие углы при пересечении прямых а║в секущей с, тогда они равны по ____________. Если . Ч.т.д.
1) Второе свойство параллельных прямых; соответственные; вертикальные углы; по 1 свойству параллельных прямых.
2) Второй признак параллельных прямых; равны; вертикальные углы; по 1 свойству параллельных прямых.
3) Первое свойство параллельных прямых; в сумме составляют 180°; соответственные углы; по 2 свойству параллельных прямых.
4) Второе свойство параллельных прямых; равны; вертикальные углы; по 1 свойству параллельных прямых
5) Второе свойство параллельных прямых; равны; вертикальные углы; по 1 признаку параллельных прямых.
Задание 23 Заполните пропуски в формулировке теоремы
Если стороны одного угла _______________________перпендикулярны __________________________другого угла, то
Задание 24 Найдите градусные меры углов 1 и 2 (рисунок №9), если , а
Впишите ответы в таблицу, по номерам кроме 23 задания.
Количество верных ответов ______________________
Задание 1 На рисунке изображены прямые а , в и секущая с . Какое условие должно выполняться, чтобы прямые а и в были параллельны (рисунок №1).
Задание 2 Выберите верные утверждения.
1) Если две прямые параллельны третьей прямой, то они параллельны между собой.
2) Если при пересечении двух прямых секущей соответственные углы составляют 180°, то прямые параллельны.
3) Если при пересечении двух прямых секущей вертикальные углы равны, то прямые параллельны.
4) Если две параллельные прямые пересечены секущей, то накрест лежащие углы составляют 180°.
5) Через точку вне прямой проходит только одна прямая, параллельная данной прямой.
Задание 3 Прямые l и f параллельны , m и n – секущие (рисунок №2). Выберите верные утверждения.
Задание 4 Выберите неверное утверждение.
1) При пересечении двух параллельных прямых секущей образуется две пары накрест лежащих углов, две пары односторонних углов и четыре пары соответственных углов.
2) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
3) Через точку, не лежащую на данной прямой проходит только одна прямая, параллельная данной.
4) Если две параллельные прямые пересечены секущей, то накрест лежащие углы составляют 180°.
5) Если две прямые на плоскости не имеют общих точек, то они параллельны.
Задание 5 Данное утверждение «Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны» является:
1) Первым свойством параллельных прямых.
2) Первым признаком параллельных прямых.
3) Вторым признаком параллельных прямых.
4) Вторым свойством параллельных прямых.
5) Третьим признаком параллельных прямых.
Задание 6 Прямые а║в, c ║ d (рисунок №3) . Какое равенство является неверным.
Задание 7 Если прямые r и x параллельны (рисунок №4), то неверно …
Задание 8 Аксиома параллельных прямых – это аксиома …
1) Ломоносова. 2) Пифагора. 3) Лобачевского. 4) Евклида. 5)Архимеда.
Задание 9 Теорема « Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны» является для теоремы « Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны» ….
2) Обратной теоремой.
Задание 10 В теореме « Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны», различают две части, которые называются:
1) Достаточное и необходимое условия.
2) Начало и конец.
3) Первая часть и вторая часть.
4) Условие и заключение.
5) Прямая и обратная части.
Задание 11 Рисунок соответствует доказательству (рисунок №5.2)….
1) Свойству параллельных прямых через односторонние углы.
2) Следствию, о том, что прямая, пересекающая одну из параллельных прямых, пересекает и другую.
3) Признака параллельности прямых через соответственные углы.
4) Следствия, о том, что если две прямые параллельны третьей прямой, то они параллельны.
5) Свойства параллельных прямых через соответственные углы.
Задание 12 Определение параллельных прямых формулируется так …
1) Через точку, не лежащую на данной прямой, проходит только одна прямая параллельная данной
2) Две прямые на плоскости называются параллельными, если они не пересекаются.
3) Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и к другой.
4) Через любые две точки проходит прямая, и притом только одна.
5) Если две прямые перпендикулярны третьей прямой, то они параллельны.
Задание 13 При доказательстве свойства параллельных прямых через накрест лежащие углы использую метод …
3) от противного
5) от простого к сложному.
Задание 14 Для построения параллельных прямых на практике не используют:
1) линейка и циркуль
Задание 15 Какой теореме соответствует данное доказательство (рис №6.3).
«Так как прямые m ║ n , то соответственные углы 1 и 2 равны по второму свойству параллельных прямых. Углы 2 и 4 смежные , тогда их сумма равна 180° по свойству смежных углов, поэтому . Но , тогда из полученных равенств следует ч.т.д.
1) Свойство соответственных углов, образованных при пересечении параллельных прямых секущей.
2) Признак параллельности прямых через односторонние углы.
3) Свойство накрест лежащих углов, образованных при пересечении параллельных прямых секущей.
4) Свойство односторонних углов, образованных при пересечении параллельных прямых секущей.
5) Признак параллельности прямых через соответственные углы.
Задание 16 При пересечении двух параллельных прямых секущей один из образованных углов на рисунке равен 123°. Найдите углы (рисунок №7)
Задание 17 Продолжите предложение, чтобы оно стало верным утверждением : « Если прямая пересекает одну их двух параллельных прямых, то …»
1) они все параллельны;
2) она пересекает и другую;
3) она параллельна к другой;
4) они все пересекутся в одной точке;
5) она составляет с другой прямой угол.
Задание 18 Если прямые r и x параллельны, . Найдите градусные меры углов (рис №4)
Задание 19 Укажите теорему, которая имеет условие — «параллельные прямые пересечены секущей», заключение – «односторонние углы в сумме составляют 180°».
1) Если две параллельные прямые пересечены секущей, то сумма односторонних углов не равна 180°.
2) Если при пересечении двух прямых секущей односторонние углы в сумме составляют 180°, то прямые параллельны.
3) Если при пересечении двух прямых секущей односторонние углы в сумме составляют 180°, то прямые не параллельны.
4) Если две прямые пересечены секущей, то сумма односторонних углов равна 180°.
5) Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
Задание 20 Укажите теорему, которая является обратной для теоремы с условием « две параллельные прямые пересечены секущей» и заключением «сумма односторонних углов равна 180°».
1) Если две прямые пересечены секущей, то сумма односторонних углов не равна 180°.
2) Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
3) Если при пересечении двух прямых секущей сумма односторонних углов равна 180° , то прямые параллельны.
4) Если односторонние углы при пересечении двух прямых секущей в сумме не составляют 180°, то прямые не параллельны.
5) Недостаточно данных.
Задание 21 На каком из пяти рисунков (рис №8) прямые m и n параллельны по признаку « Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны».
Задание 22 К какой теореме относится это доказательство, дополните его, чтобы рассуждения были верными (рис №10.4).
Известно, что прямые а║в пересечены секущей с. Докажем, что сумма углов 1 и 2 равна 180°.
На рисунке углы 1 и 3 –______________, значит они в сумме равны 180°. Углы 2 и 3 ______________ углы при пересечении прямых а║в секущей с, тогда они равны по ____________. Если . Ч.т.д.
1) Третье свойство параллельных прямых; смежные углы; соответственные; по 1 свойству параллельных прямых.
2) Третий признак параллельных прямых; смежные углы; соответственные; по 1 свойству параллельных прямых.
3) Третье свойство параллельных прямых; смежные углы; накрест лежащие; по 1 свойству параллельных прямых.
4) Третье свойство параллельных прямых; смежные углы; накрест лежащие; по 1 признаку параллельных прямых.
5) Первый признак параллельных прямых; односторонние углы; накрест лежащие; по 1 признаку параллельных прямых.
Задание 23 Сформулируйте любое следствие из аксиомы параллельных прямых.
4 вариант. Найдите градусные меры углов 1 и 2 (рис №9), если , а
Видео:Прямые m и n параллельны. Найдите ∠3, если ∠1=24°, ∠2=90° | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

На рисунке 88, б прямые а и b пересекают стороны треугольника ABC так, что угол 5 = углу 6, а угол 7 = углу 8. а) Докажите, что прямые а и АС параллельны. б) Верно ли, что b || АВ?
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Ваш ответ
Видео:№36. Прямая с пересекает прямую а и не пересекает прямую b, параллельную прямой а.Скачать

решение вопроса
Видео:ВСЕ правила и формулы ПЛАНИМЕТРИИСкачать

Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,688
- разное 16,822
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Параллельные прямые — Признак Параллельности Прямых и Свойства УгловСкачать

Геометрия. 7 класс
Определение
Выберите верное продолжение определения.
Две прямые на плоскости называются параллельными, если они
имеют одну общую точку
имеют две общих точки
Свойства углов
На рисунке ∠1 = 100°. Заполните на основании рисунка пропуски в тексте.
Углы ∠1 + ∠2 = ° по свойству углов, ∠1 = ∠4 (по свойству углов). Значит, ∠2 = °, ∠3 = °, ∠4 = °.
Выберите признак
Соедините линиями каждый признак параллельных прямых и соответствующий ему чертёж.
Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
Виды углов
Подставьте названия углов к соответствующим изображениям.
Параллельные прямые
Отметьте, на каких рисунках представлены пары параллельных прямых.
Параллельны или перпендикулярны
Выберите правильный ответ из выпадающего списка.
На плоскости, если a ║ b, c┴a, то:
Взаимное расположение прямых
Перетащите верный ответ.
Если a || b, b || c, то прямая а с.
Докажите
Докажите, что прямые параллельны. Выделите цветом утверждения, соответствующие рисунку.
Прямые параллельны / не параллельны , так как накрест лежащие углы равны / соответственны/ углы равны / сумма односторонних углов равна 180°
Три прямые
Посмотрите на рисунок. Подчеркните верное утверждение.
Параллельны ли прямые?
Можно ли утверждать, что на рисунке есть параллельные прямые? Выберите правильные ответы возле рисунков.


Докажите признак
Восстановите последовательность этапов доказательства признака параллельности прямых: если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
следовательно, a║b по теореме 1.
∠1 +∠2 = 180° по условию, откуда ∠1 = 180° – ∠2
∠3 + ∠2 = 180° – по свойству смежных углов, откуда ∠3 = 180° – ∠2
∠1 = ∠3 = 180° – ∠2, это накрест лежащие углы
Докажите
Найдите правильную последовательность доказательства параллельности прямых.
- Это накрест лежащие углы, значит прямые a и b параллельные.
- Δ ABK = ΔCDK по двум сторонам и углу между ними
- AK = CK, BK = KD, ∠AKB = ∠CKD – вертикальные
- из равенства треугольников следует ∠ABK = ∠CDK
Подчеркните верный ответ.
Выделите цветом верный ответ
Установите взаимное расположение прямой AB и биссектрисы CD угла BCК.
Прямые AB и CD параллельны / не параллельны
Четырехугольник
Введите с клавиатуры недостающие элементы текста.
В четырёхугольнике ABCD все стороны равны. Укажите, из равенства каких углов можно сделать вывод о параллельности его сторон.
📺 Видео
№45. Прямая а параллельна стороне ВС параллелограмма ABCD и не лежит в плоскости параллелограмма.Скачать

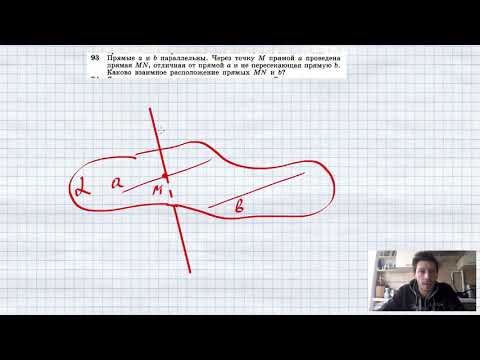
№93. Прямые а и b параллельны. Через точку М прямой a проведена прямая MN, отличная от прямой а и неСкачать
ОГЭ Математика 2024 Ященко | Вариант 2 | Полный разборСкачать

Вся ГЕОМЕТРИЯ ОГЭ | ВЕБИНАР |TutorOnlineСкачать

В-1 № 101-185 - Геометрия 7 класс Мерзляк дидактические материалыСкачать

№16. Параллельные прямые a и b лежат в плоскости α. Докажите,Скачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Полный разбор варианта №2 из сборника Ященко | Математика ОГЭ 2024 #сотка #огэ2024 #сборникЯщенкоСкачать

ЕГЭ 2022 Ященко 5 вариант ФИПИ школе полный разбор!Скачать

Параллельные прямые. 6 класс.Скачать

Разбор ОГЭ по Математике 2024. Вариант 22 Ященко. Куценко Иван. Онлайн школа EXAMhackСкачать

Вариант #13 из задач ФИПИ - Уровень Сложности ЕГЭ 2024| Математика Профиль| Оформление на 100 БалловСкачать

№ 40130 РешуЕгэ найти абсциссу точки, в которой касательная к графику функции параллельна прямойСкачать

Задание 5 ОГЭ по математикеСкачать

















