Провести фронталь на расстоянии 20 мм от плоскости п2 и пересекающую параллельные прямые

Видео:Провести горизонтальную прямую через точку и пересекающую заданный отрезок. Начертательная геометрияСкачать

Рабочая тетрадь для решения задач

по дисциплинe «Начертательная геометрия»

(для студентов заочной формы обучения)

Тема 1. Изображение точек на комплексном чертеже.

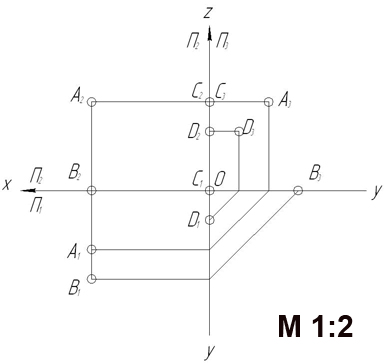
З а д а ч а 1. Построить точки А(40,20,30), В(40,30,0), С(0,0,30) и D(0,10,20) на комплексном чертеже.

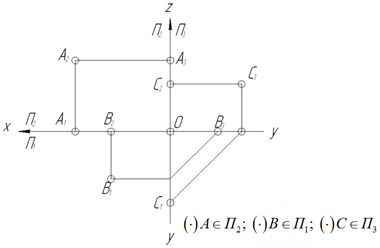
З а д а ч а 2. Точки А, В и С принадлежат плоскостям проекций. Построить недостающие проекции этих точек и указать в какой плоскости каждая из них располагается.

Тема 2. Прямая. Взаимное расположение прямых.

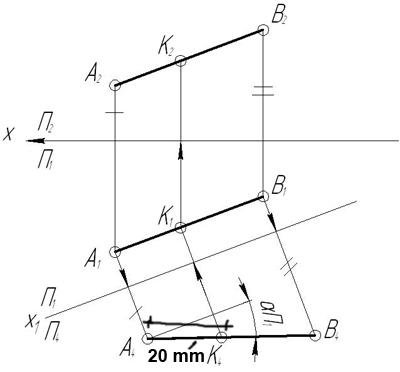
З а д а ч а 3. Даны точки А(90,30,40), В(10,20,15), С(60,20,40) и D(30,40,15). Построить отрезки АВ и СD, обозначить и записать координаты конкурирующих точек.

З а д а ч а 4. Отложить на отрезке АВ отрезок АК=20мм и определить угол наклона отрезка АВ к плоскости проекций П₁.

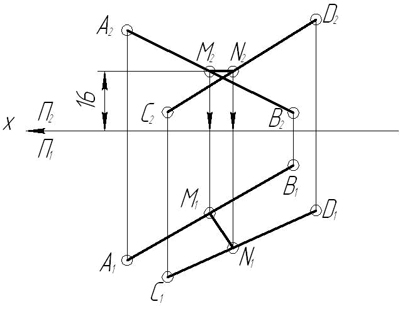
З а д а ч а 5. Пересечь прямые АВ и СD прямой MN, отстоящей от плоскости П₁ на расстоянии 16 мм.

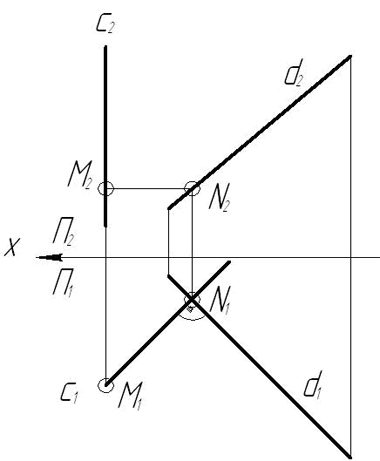
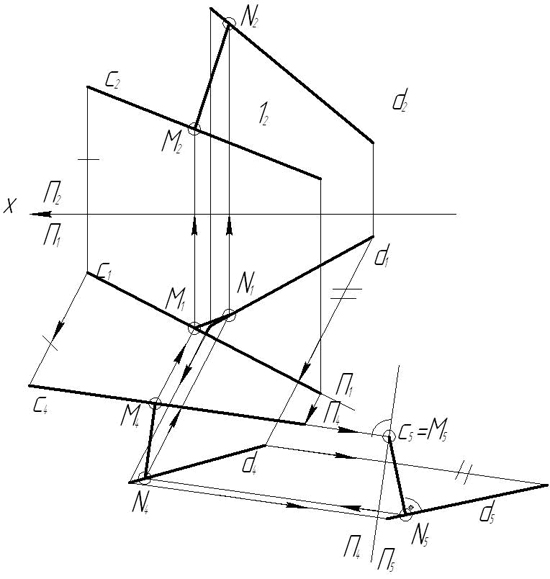
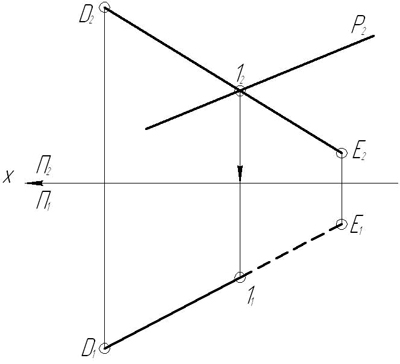
З а д а ч а 6. Даны две скрещивающиеся прямые с и d. Построить отрезок МN, являющийся кратчайшим расстоянием между этими прямыми.

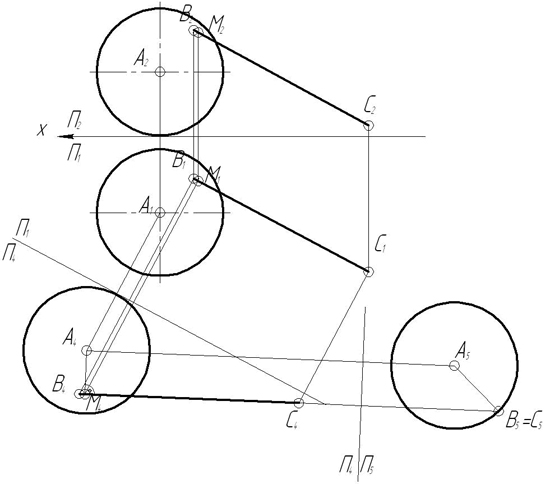
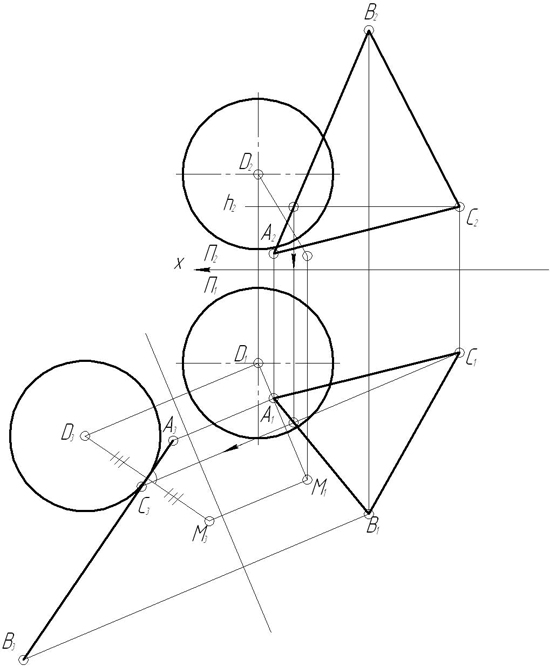
З а д а ч а 7. Дано: точка А(А₁,А₂) и прямая ВС общего положения. Построить сферу с центром в точке А, касательную к прямой ВС

Тема 3. Плоскость. Главные линии плоскости.

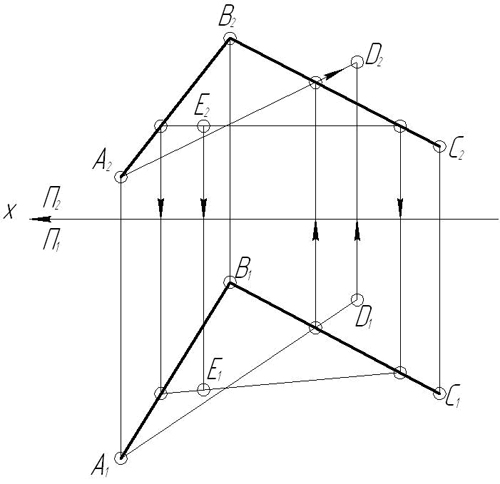
З а д а ч а 8. Дана плоскость сигма (ΔABC), точки D и E в этой плоскости. Через точку Е провести горизонталь h, через точку D – фронталь f этой плоскости.

З а д а ч а 9. Построить недостающие проекции точек E и D, лежащих в плоскости сигма (АВ ∩ ВС).

З а д а ч а 10. Дан плоский пятиугольник ABCDЕ, заданный горизонтальной и фронтальной проекциями двух смежных сторон. Достроить его фронтальную проекцию.

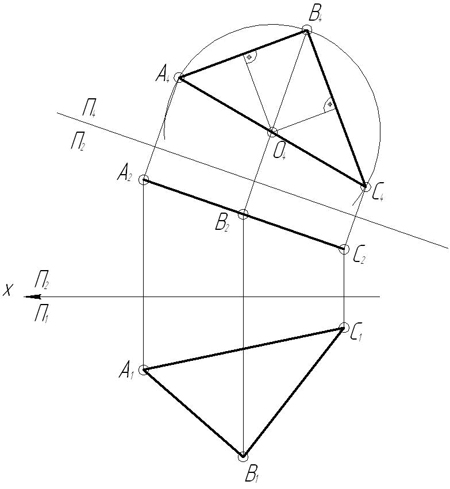
З а д а ч а 11. Дан треугольник АВС. Найти центр окружности, описанной вокруг заданного треугольника.

Тема 4. Взаимное расположение прямой и плоскости.

З а д а ч а 12. Задана плоскость Р и прямая DE. Найти точку пересечения прямой с плоскостью. Определить видимость проекции прямой. (Р₂ – фронтальный след плоскости). P (AB//FC).

З а д а ч а 13. Заданы плоскость Р(ΔАВС) и точка D: а) определить расстояние от точки D до плоскости Р; б) построить точку М, симметричную точке D относительно плоскости Р; в) построить шар с центром в точке D, касательный к плоскости Р.

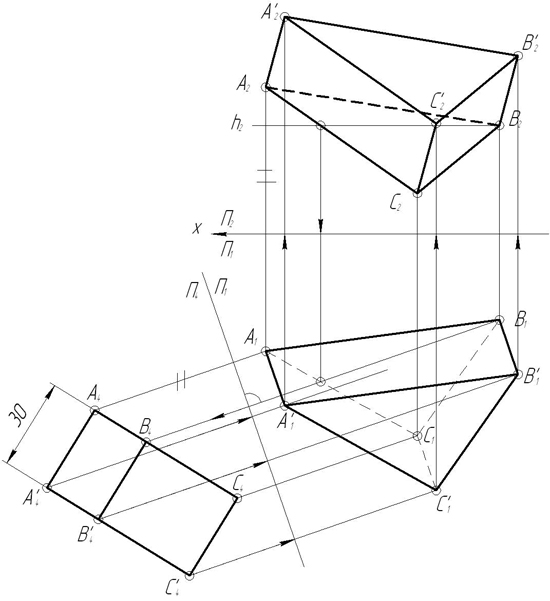
З а д а ч а 14. Задан ΔАВС общего положения. Построить прямую призму с основанием ΔАВС и высотой равной 30 мм.

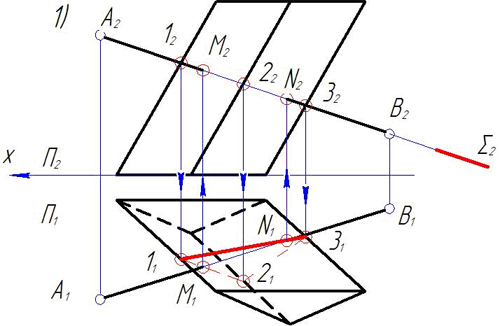
Тема 5. Взаимное положение плоскостей.

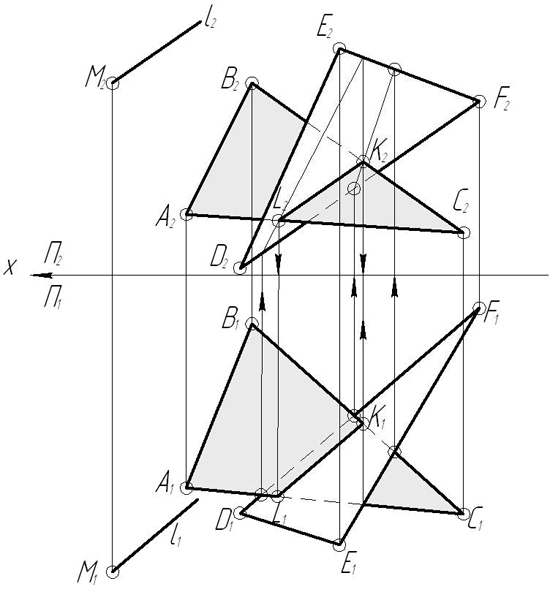
З а д а ч а 15. Даны плоскости сигма(ΔАВС), гамма(DEF) и точка М: а) построить линию пересечения плоскостей. б) через точку М провести прямую l, параллельную плоскостям сигма и гамма. Задачу решить без использования способа замены плоскостей.

З а д а ч а 16 Даны плоскость Р(а//b) и точка М. Через точку М провести плоскость Г, параллельную плоскости Р.

З а д а ч а 17 Даны плоскость Р(а//b) и прямая CD. Через прямую CD провести плоскость Г перпендикул. Р. Г(ΔСDE)

З а д а ч а 18

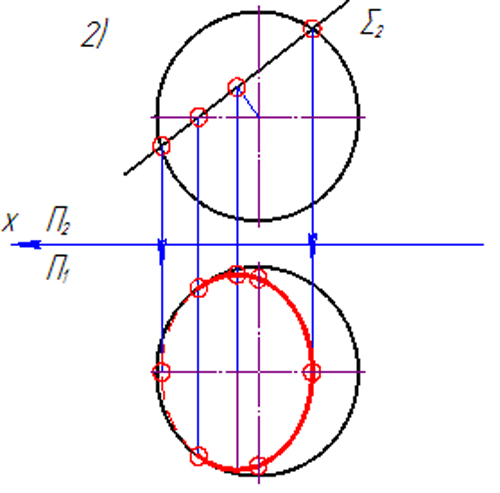
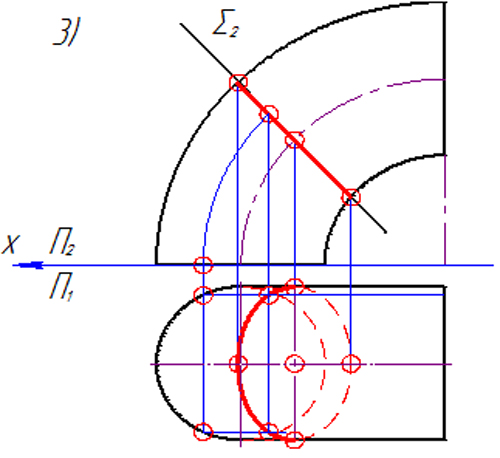
Тема 7. Пересечение поверхности с плоскостью

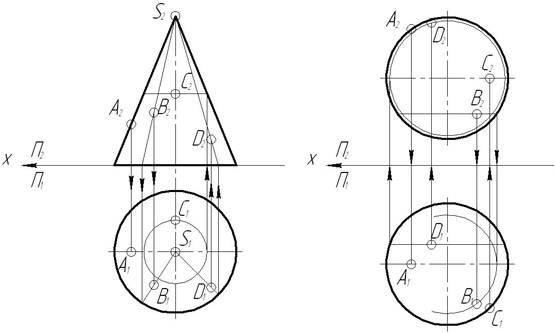
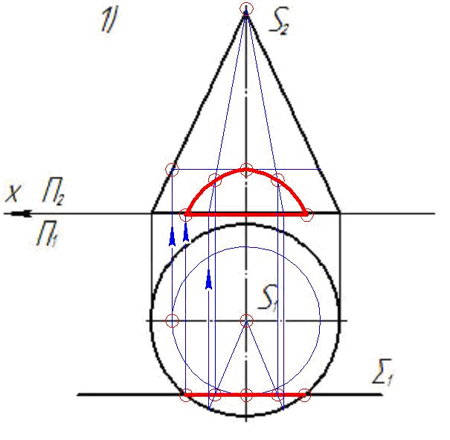
З а д а ч а 19. Построить проекции сечения данной поверхности проецирующей плоскостью Σ.

Тема 8. Пересечение прямой линии с поверхностью

З а д а ч а 20. Построить точки пересечения прямой с заданной поверхностью. Установить видимость проекций прямой

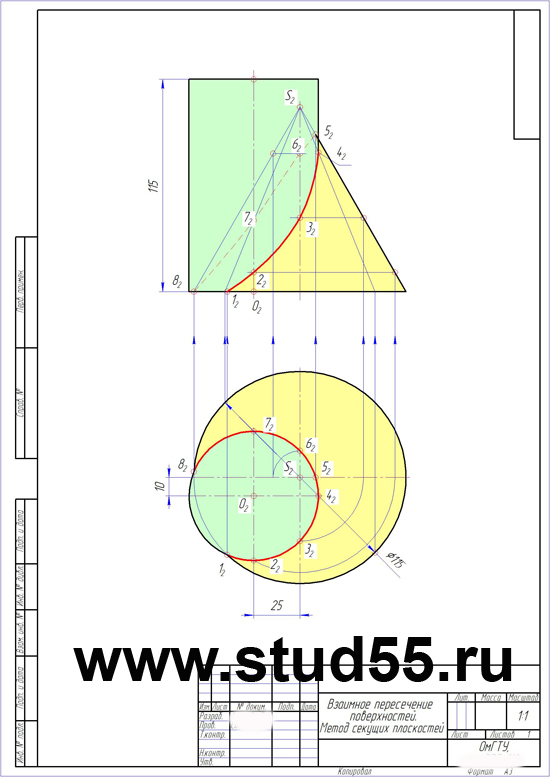
Тема 10. Взаимное пересечение поверхностей.

З а д а ч а 21 Метод вспомогательных секущих плоскостей

З а д а ч а 22 Метод сферического посредника

Видео:Параллельность прямой к плоскостиСкачать

Начертательная геометрия. Инженерная графика. Практикум для студентов вузов (стр. 3 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9

Цель занятия — научиться:

1) выполнять чертеж линии;

2) определять положение линии в пространстве относительно плоскостей проекций;

3) определять взаимное положение линий;

4) определять по чертежу натуральную величину отрезка и углы наклона его к плоскостям проекций.

Линию следует рассматривать как траекторию перемещения точки. Линии могут быть пространственные и плоские.

Пространственными линиями называют линии, все точки которых не принадлежат одной плоскости.

Линии, у которых все точки принадлежат одной плоскости, называют плоскими.

Простейшей линией является прямая. При ортогональном проецировании на плоскость прямая проецируется в прямую. Поэтому для определения ее проекции достаточно знать проекции двух нетождественных точек, принадлежащих этой прямой.

След прямой — это точка пересечения прямой с плоскостью проекций. Точку пересечения прямой с горизонтальной плоскостью проекций называют горизонтальным следом прямой, с фронтальной — фронтальным следом прямой, с профильной — профильным следом прямой.

Прямая может занимать следующие положения относительно плоскостей проекций:

1. Прямые общего положения — это плоскости не параллельные и не перпендикулярные ни одной из плоскостей проекций.

а) проецирующие прямые — прямые, перпендикулярные к какой-либо плоскости проекций и параллельные к другим двум;

б) прямые уровня — прямые, параллельные какой-либо плоскости проекций;

в) прямые, принадлежащие плоскости проекций — частный случай прямых уровня.

Примеры решения задач

Пример 1. Построить прямую, проходящую через точки А и В. Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Чтобы построить горизонтальный (фронтальный) след прямой, нужно продолжить фронтальную (горизонтальную) проекцию прямой до пересечения с осью x и, используя принцип принадлежности точки прямой, достроить недостающие проекции (по соответствующим линиям связи) (рис. 7).

AB — прямая общего положения;

M — горизонтальный след;

N — фронтальный след.

AB — прямая частного положения, прямая уровня, профильная прямая;

M — горизонтальный след;

N — фронтальный след;

β — угол наклона к плоскости V;

γ — угол наклона к плоскости H.

Пример 2. Определить взаимное положение прямых а и в в пространстве на рис. 8 а, б, в.

Если прямые в пространстве параллельны, то на чертеже параллельны их одноименные проекции.

Если прямые в пространстве пересекаются, то на чертеже пересекаются их одноименные проекции. При этом проекции точки пересечения лежат на одной линии связи.

Если прямые в пространстве скрещиваются, то на чертеже их одноименные проекции могут пересекаются, но проекции точек пересечения не лежат на одной линии связи.

Пример 3. Определить натуральную величину (НВ) отрезка АВ (рис. 9) методом прямоугольного треугольника и углы наклона его к плоскостям проекций.

Натуральная величина отрезка общего положения равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция на одну из плоскостей проекций, а другим — разность расстояний концов отрезка от этой же плоскости.

Угол между катетом — проекцией и гипотенузой прямоугольного треугольника равен истинной величине угла наклона отрезка к той плоскости проекций, на которой выполнены построения.

АВ — прямая общего положения;

А0В′ = А0В′′ = А″′В0 = НВ;

α — угол наклона отрезка АВ к горизонтальной плоскости проекций;

β — угол наклона отрезка АВ к фронтальной плоскости проекций;

γ — угол наклона отрезка АВ к профильной плоскости проекций.

Задания для самостоятельного решения

Задача 1. Построить прямую, проходящую через точки А (50, 15, 40), В (0, 55, 5). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить горизонталь, удаленную от плоскости H на 35 мм и расположенную под углом 25° к плоскости W.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (25, 30, 5), В (25, 0, 10). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить фронталь, удаленную от плоскости V на 25 мм и расположенную под углом 35° к плоскости H.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (15, 30, 10), В (40, 20, 20). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить фронталь, удаленную от плоскости V на 10 мм и расположенную под углом 40° к плоскости H.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (20, 30, 10), В (50, 5, 10). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить фронталь, удаленную от плоскости V на 15 мм и расположенную под углом 35° к плоскости H.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (20, 10, 10), В (35, 20, 10). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить горизонталь, удаленную от плоскости H на 25 мм и расположенную под углом 45° к плоскости V.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (15, 0, 30), В (25, 10, 50). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить профильную прямую, удаленную от плоскости W на 25 мм и расположенную под углом 30° к плоскости H.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (10, 40, 5), В (0, 15, 25). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить фронталь, удаленную от плоскости V на 40 мм и расположенную под углом 60° к плоскости W.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (50, 20, 15), В (10, 20, 15). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить фронталь, удаленную от плоскости V на 35 мм и расположенную под углом 45° к плоскости H.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (40, 10, 10), В (10, 20, 20). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить горизонталь, удаленную от плоскости H на 10 мм и расположенную под углом 25° к плоскости W.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (25, 30, 15), В (25, 30, 40). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить горизонталь, удаленную от плоскости H на 45 мм и расположенную под углом 20° к плоскости V.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (50, 40, 5), В (25, 15, 10). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить профильную прямую, удаленную от плоскости W на 30 мм и расположенную под углом 55° к плоскости V.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (5, 10, 15), В (40, 60, 5). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить горизонталь, удаленную от плоскости H на 45 мм и расположенную под углом 45° к плоскости V.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (35, 0, 40), В (35, 20, 40). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить горизонталь, удаленную от плоскости H на 15 мм и расположенную под углом 30° к плоскости V.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (30, 0, 25), В (30, 15, 25). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить горизонталь, удаленную от плоскости H на 25 мм и расположенную под углом 15° к плоскости V.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (45, 20, 5), В (25, 0, 5). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить профильную прямую, удаленную от плоскости W на 25 мм и расположенную под углом 30° к плоскости V.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (50, 0, 20), В (35, 10, 45). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить горизонталь, удаленную от плоскости H на 45 мм и расположенную под углом 10° к плоскости V.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (20, 35, 5), В (10, 0, 25). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить фронталь, удаленную от плоскости V на 15 мм и расположенную под углом 45° к плоскости W.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (20, 30, 15), В (0, 30, 10). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить фронталь, удаленную от плоскости V на 40 мм и расположенную под углом 10° к плоскости H.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (40, 50, 20), В (5, 10, 0). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить горизонталь, удаленную от плоскости H на 25 мм и расположенную под углом 60° к плоскости V.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (20, 15, 0), В (70, 45, 20). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить горизонталь, удаленную от плоскости H на 25 мм и расположенную под углом 75° к плоскости V.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (0, 15, 10), В (15, 0, 25). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить фронталь, удаленную от плоскости V на 40 мм и расположенную под углом 15° к плоскости W.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (10, 40, 5), В (50, 10, 45). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить горизонталь, удаленную от плоскости H на 45 мм и расположенную под углом 15° к плоскости W.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (25, 40, 0), В (5, 10, 0). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить фронталь, удаленную от плоскости V на 40 мм и расположенную под углом 45° к плоскости W.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (10, 40, 5), В (30, 15, 25). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить горизонталь, удаленную от плоскости H на 55 мм и расположенную под углом 60° к плоскости V.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (10, 25, 30), В (40, 30, 20). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить профильную прямую, удаленную от плоскости W на 20 мм и расположенную под углом 35° к плоскости V.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (5, 20, 15), В (30, 5, 60). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить горизонталь, удаленную от плоскости H на 40 мм и расположенную под углом 35° к плоскости V.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Видео:Строим фронталь и горизонталь в плоскости общего положения удаленную от П1 П2 на какое то расстояниеСкачать

Тест/экзамен online

Пример. В плоскости, заданной двумя параллельными прямыми АВ и CD, провести фронталь на расстоянии 15 мм от фронтальной плоскости проекций (рис. 3.24)

Точка движется по прямой неравномерно (ускоренно). Как меняется ее количество движения?

Решение. Проводим на расстоянии 15 мм от оси проекций параллельную ей горизонтальную проекцию (11-22) фронтали, которая пересекает прямые А1В1 и C1D1 в точках 11 и 22.

Затем находим точки 11 и 22 на прямых А2В2 и C2D2 и проводим через них фронтальную проекцию (1222) фронтали.

Пример 5. Найти прямую пересечения плоскостей Р и Q.

Решение. Плоскость Р и Q пересекаются по прямой общего положения, проходящей через точку-след (М1;М2) пересечения горизонтальных следов плоскостей. Точка-след (N1;N2) пересечения фронтальных следов плоскостей недоступна, т.к. эти следы плоскостей по заданию, в пределах чертежа не пересекаются.

Вместо точки (N1;N2) необходимо найти другую произвольную точку прямой пересечения, общую для заданных плоскостей. Для этого вводим вспомогательную плоскость R, например параллельную П которая, как известно, пересекает каждую из данных плоскостей по горизонтали. На их пересечении получаем вспомогательную точку (К1;К2), общую для данных плоскостей. Найдя эту вторую точку (К1;К2) прямой, проводим её проекцию: горизонтальную – через точки М1 и К1 и фронтальную через точки М2 и К2.

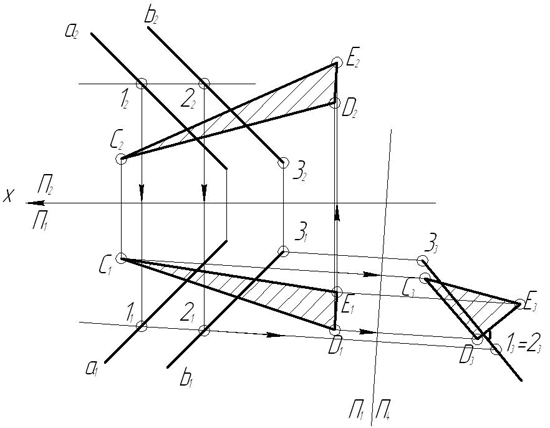
Пример 6. Найти точку пересечения прямой АВ с плоскостью Р (рис. 3.26)

Решение. Обозначим искомую точку через точку К. Так как точка К (К1;К2) лежит на профильно-проецирующей плоскости. То её профильная проекция (К3) должна лежать на профильном следе (Р3) плоскости. Вместе с тем, так как эта же точка лежит и на прямой АВ, то её профильная проекция (К3) должна лежать так же где-то на профильной проекции (А3В3) прямой. Следовательно искомая точка должна лежать на их пересечении. Найдя профильный след плоскости и профильную проекцию прямой, получаем на их пересечении профильную проекцию (К3) искомой точки. Зная профильную проекцию (К3) искомой точки, находим две другие её проекции на одноименных проекциях прямой.

Пример 7. Даны плоскость Р и точка А. Определить расстояние то точки до плоскости (рис. 3.27)

Решение. Опускаем из точки А (А1;А2) перпендикуляр на плоскость Р и находим его основание на этой плоскости, для чего ищем точку К (К1;К2) пересечения перпендикуляра с плоскостью. Имея проекции (А1К1;А2К2) отрезка перпендикуляра, определим его действительную величину методом прямоугольного треугольника.

Пример 8. Даны треугольник АВС и точка К. Определить расстояние между ними. (рис. 3.28)

Решение. Опускаем из заданной точки Е (Е1;Е2) перпендикуляр на плоскость треугольника: К1Е1 перпендикулярно горизонтальной проекции горизонтали (К1Е1С1F1), К2Е2 перпендикулярно фронтальной проекции фронтали (К2Е2А2 D2). Находим точку пересечения перпендикуляра с плоскостью треугольника (К1;К2) , определяем натуральную величину отрезка перпендикуляра (К1Е1;К2Е2) методом прямоугольного треугольника.

🎬 Видео

Горизонталь в плоскостиСкачать

Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать

Главные линии плоскости - фронталь f и горизонталь hСкачать

Построение параллельной плоскости на расстояние 30 мм.Скачать

Задача 3.3. Через точку М провести горизонталь и фронталь.Скачать

Проецирование прямой общего положенияСкачать

Частное положение точек. Точки принадлежащие к плоскостям проекции.Скачать

Построить проекции линии и точек на ней по заданным координатам. Начертательная геометрияСкачать

Определение кратчайшей расстоянии от точки до плоскостиСкачать

Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Точка встречи прямой с плоскостьюСкачать

ПРЯМЫЕ ЧАСТНОГО ПОЛОЖЕНИЯ. Фронталь, горизонталь и профильная. Разбор тестовых задач по начерталкеСкачать

Способ замены (перемены) плоскостей проекции. Определение истинной величины отрезка и плоской фигурыСкачать

Построение следов плоскостиСкачать

Построение параллельной плоскости на расстояние 40 мм. Плоскость задана со следами.Скачать

ФРОНТАЛЬ И ЕЕ ПРОЕКЦИИ. Задача. Начертательная геометрия. Техническая графикаСкачать