Против большей стороны треугольника лежит больший угол если стороны одного четырехугольника

Какие из данных утверждений верны? Запишите их номера.

1) Против большей стороны треугольника лежит больший угол.

2) Любой прямоугольник можно вписать в окружность.

3) Площадь треугольника меньше произведения двух его сторон.

Проверим каждое из утверждений.

1) «Против большей стороны треугольника лежит больший угол» — верно, по свойству треугольника.

2) «Любой прямоугольник можно вписать в окружность» — верно; выпуклый четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположных углов этого четырёхугольника равна 180°.

3) «Площадь треугольника меньше произведения двух его сторон» — верно, поскольку площадь треугольника можно вычислить по формуле , где a и b — стороны треугольника, а — угол между этими сторонами. Так как не может быть больше 1, то и S не может превышать полупроизведения сторон.

Четвертый признак равенства треугольников

Четвертый признак равенства треугольников — это признак,
c помощью которого можно доказать, что треугольники равны.

С помощью четвертого признака равенства можно решить
любую из задач, где требуется доказать, что треугольники равны.

Формулировка:

Если две стороны и угол, лежащий против большей из сторон
одного треугольника соответственно равны двум сторонам и углу,
лежащему против большей из сторон другого треугольника,
то такие треугольники равны.

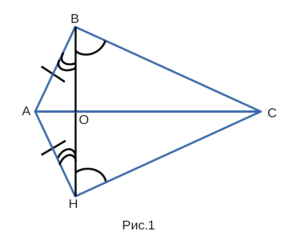
Докажем, что △ABC и △FHE равны между собой. Для этого
совместим их так, как показано на рисунке 1.

Доказательство:

1. Рассмотрим △ABC и △FHE, которые наложились друг на друга,
   AВ = AH,∠ABO = ∠AHO, ∠BOC = ∠HOC. Докажем, что △ABC = △FHE.
2. △ABH — равнобедренный (AB = AH), значит ∠ABO = ∠AHO.
3. ∠BOC = ∠HOC, так как остатки равных углов.
4. △BHC — равнобедренный(∠BOC = ∠HOC), а так как углы при боковых
   сторонах HC и BC равны, значит HC = BC.
5. Итак, △ABC = △FHE по двум сторонам и углу, лежащему
   против большей из сторон.

Свойства сторон и углов треугольника

Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.

Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .

Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.

a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.

Сумма углов треугольника равна 180°

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Величина большего угла треугольника не может быть меньшей, чем 60°.

,

где α – больший угол треугольника.

Величина меньшего угла треугольника не может быть большей, чем 60°.

,

где β – меньший угол треугольника.

,

Фигура	Рисунок	Формулировка
Треугольник
Большая сторона треугольника		Против большей стороны треугольника лежит больший угол
Больший угол треугольника		Против большего угла треугольника лежит большая сторона
Меньшая сторона треугольника		Против меньшей стороны треугольника лежит меньший угол
Меньший угол треугольника		Против меньшего угла треугольника лежит меньшая сторона
Длины сторон треугольника
		Углы треугольника
Внешний угол треугольника
Больший угол треугольника
Меньший угол треугольника
Теорема косинусов
Теорема синусов

Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.

Определение . Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .

Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.

a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.

Сумма углов треугольника равна 180°

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Величина большего угла треугольника не может быть меньшей, чем 60°.

,

где α – больший угол треугольника.

Величина меньшего угла треугольника не может быть большей, чем 60°.

,

где β – меньший угол треугольника.

,

Треугольник
Большая сторона треугольника
	Против большей стороны треугольника лежит больший угол
Больший угол треугольника
	Против большего угла треугольника лежит большая сторона
Меньшая сторона треугольника
	Против меньшей стороны треугольника лежит меньший угол
Меньший угол треугольника
	Против меньшего угла треугольника лежит меньшая сторона
Длины сторон треугольника
	Углы треугольника
Внешний угол треугольника
Больший угол треугольника
Меньший угол треугольника
Теорема косинусов
Теорема синусов

Треугольник

Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.

Определение . Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .

Большая сторона треугольника

Свойство большей стороны треугольника:

Против большей стороны треугольника лежит больший угол

Больший угол треугольника

Свойство большего угла треугольника:

Против большего угла треугольника лежит большая сторона

Меньшая сторона треугольника

Свойство меньшей стороны треугольника:

Против меньшей стороны треугольника лежит меньший угол

Меньший угол треугольника

Свойство меньшего угла треугольника:

Против меньшего угла треугольника лежит меньшая сторона

Длины сторон треугольника

Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.

a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.

Углы треугольника

Свойство углов треугольника:

Сумма углов треугольника равна 180°

Внешний угол треугольника

Свойство внешнего угла треугольника:

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Больший угол треугольника

Свойство большего угла треугольника:

Величина большего угла треугольника не может быть меньшей, чем 60°.

,

где α – больший угол треугольника.

Меньший угол треугольника

Свойство меньшего угла треугольника:

Величина меньшего угла треугольника не может быть большей, чем 60°.

,

где β – меньший угол треугольника.

Теорема косинусов

Теорема синусов

Свойство меньшего угла треугольника:

,

📽️ Видео