В данной публикации мы рассмотрим одну из основных теорем по геометрии 8 класса – теорему Фалеса, которая получила такое название в честь греческого математика и философа Фалеса Милетского. Также разберем пример решения задачи для закрепления изложенного материала.
Видео:Пропорциональные отрезки. Теорема о пропорциональных отрезкахСкачать

Формулировка теоремы
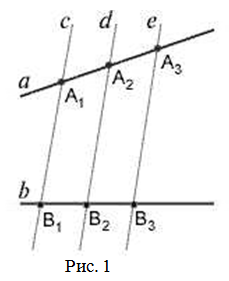
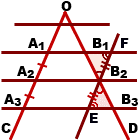
Если на одной из двух прямых отмерить равные отрезки и через их концы провести параллельные прямые, то пересекая вторую прямую они отсекут на ней равные между собой отрезки.
Примечание: Взаимное пересечение секущих не играет роли, т.е. теорема верна и для пересекающихся прямых, и для параллельных. Расположение отрезков на секущих, также, не важно.
Обобщенная формулировка
Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках*: параллельные прямые отсекают на секущих пропорциональные отрезки.
В соответствии с этим для нашего чертежа выше справедливо следующее равенство:
* т.к. равные отрезки, в т.ч., являются пропорциональными с коэффициентом пропорциональности, равным единице.
Обратная теорема Фалеса
1. Для пересекающихся секущих
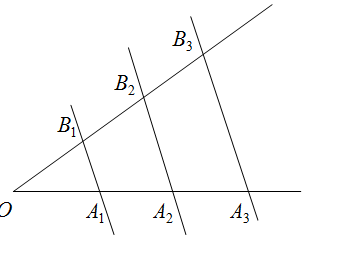
Если прямые пересекают две другие прямые (параллельные или нет) и отсекают на них равные или пропорциональные отрезки, начиная от вершины, значит эти прямые являются параллельными.
Из обратной теоремы следует:
Обязательное условие: равные отрезки должны начинаться от вершины.
2. Для параллельных секущих
Отрезки на обеих секущих должны быть равны между собой. Только в этом случае теорема применима.
Видео:Геометрия 8 класс (Урок№5 - Теорема Фалеса)Скачать

Пример задачи
Дан отрезок AB на плоскости. Разделите его на 3 равные части.
Решение
Проведем из точки A прямую a и отметим на ней три подряд идущих равных отрезка: AC, CD и DE.
Крайнюю точку E на прямой a соединяем с точкой B на отрезке. После этого через оставшиеся точки C и D параллельно BE проведем две прямые, пересекающие отрезок AB.
Образованные таким образом точки пересечения на отрезке AB делят его на три части, равные между собой (согласно теореме Фалеса).
Видео:Теорема о пропорциональных отрезкахСкачать

Теорема Фалеса
Одна из основополагающих теорем (теорема Фалеса) в геометрии говорит о том, что проведенные через концы одинаковых отрезков прямой параллельные линии отсекают на другой прямой тоже одинаковые по длине отрезки. Причем происходит это независимо от угла между прямыми. Это достаточно произвольная формулировка теоремы Фалеса, но достаточно емко описывающая ее суть. Разные учебники приводят разные формулировки, но суть остается неизменной.
Ключевые слова в теореме (при любой формулировке) — прямые, отрезки, равные, пропорциональные, параллельные. Это говорит о том, что теорема Фалеса касается только планиметрии, то есть изображения линий на плоскости. Она очень важна для картографии и навигации, широко используется в архитектуре и живописи, строительстве и проектировании.
Классической формулировки, единой в своем роде нет. Например, формулировку можно услышать в такой редакции:
Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
А можно и в такой:
Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Если внимательно присмотреться, то можно увидеть, что одно утверждение не противоречит другому, а рисунки практически идентичны. Если продолжить прямые на первом рисунке по получим тот же угол.
Кроме прямых, которые проходят под углом, такая же картина происходит при пересечении параллельных прямых. Разница состоит в том, что на пересекающихся прямых отрезки АВ и А1В1 могут быть как одинаковыми, так и пропорциональными, в зависимости от угла наклона секущих. А для случая параллельных — только одинаковыми. Если обобщить два случая, то обобщенная теорема Фалеса звучит так: Параллельные прямые отсекают на секущих пропорциональные отрезки.
Для иллюстрации можно воспользоваться рисунком 1.
Видео:8 класс, 19 урок, Пропорциональные отрезкиСкачать

Как пользоваться теоремой Фалеса на практике
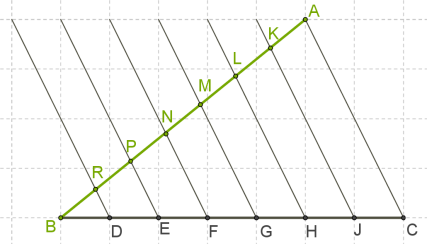
Теорема Фалеса это не только теоретическое утверждение, доказанное методами математики, но и практический инструмент для построения различных фигур. Простейшая задача — разделить на равные части произвольный отрезок ВА. Пусть этих частей будет 7.
Для решения задачи нарисуем отрезок ВС, образующий с данным ВА угол. Как видим, отрезок ВС проходит вдоль клеток на бумаге, что позволяет выбрать на нем равные отрезки. В нашем случае, это:
BD=DE=EF=FG=GH=HJ=JC.
Начиная от крайних точек А и С проведем параллельные линии, пересекающие отрезок ВА. На нем тоже получиться семь равных отрезков: BR=RP=PN=NM=ML=LK=KA.
С таким же успехом мы можем разделить отрезок на 5, 6, 4 или любое другое количество равных частей. Суть метода состоит в том, что длину отрезка ВС мы заведомо выбираем такой, чтобы его можно было легко разделить на заданное количество частей. Например, длина отрезка ВА 37 см, а его нужно разделить на 5 частей. Выбираем длину отрезка ВС в 25 см, отмечаем точки и выполняем построение по теореме Фалеса.
Видео:Пропорциональные отрезкиСкачать

Обратная теорема Фалеса
Не менее широко используется и теорема, названная обратной. То есть, доказательства требует не равность или пропорциональность отрезков, а параллельность прямых. Формулируется обратная теорема Фалеса так:
Если две или более прямых (a, b, c) отсекают от двух других прямых (d, f) равные или пропорциональные отрезки, то они параллельные.
Утверждение справедливо, независимо от того, параллельные d, f или пересекаются.
Видео:Теорема Фалеса. 8 класс.Скачать

Доказательство теоремы Фалеса
Математика, тем более, геометрия, наука точная. Каждое утверждение, кроме аксиом, требует доказательства. В геометрии под термином «теорема» подразумевается утверждение, которое доказано на базе ранее полученных знаний в виде аксиом и других теорем.
Теорема Фалеса с доказательством приведена в большинстве учебников. В отличие от теоремы Пифагора, доказательств у нее меньше, но все они четкие, понятные и аргументированные. Покажем одно из них.
Не будем повторять формулировок, продемонстрируем только ход мыслей и выполним необходимые построения:
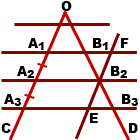
Выберем точку В2 и проведем прямую, параллельную стороне угла ОС. При этом отмечаем, что А1А3 || EF. Рассматривая четырехугольник
А1FЕА3 замечаем, что А1F и ЕА3 параллельны по определению, а А1А3 и FВ3 параллельны по построению. Отсюда вытекает, что А1 FЕА 3 — параллелограм и А1А3 = EF.
Аналогичным образом доказываем равенство других сторон и получаем, что по равенству вертикальных и внутренних углов ∠B1B2F=∠B3B2E и ∠B2FB1=∠B2EB3 треугольники B2B1F и B2B3E равны, откуда вытекает, что B1B2=B2B3.
Именно это и требовалось доказать.
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Кто впервые доказал теорему о пропорциональных отрезках
По легенде, впервые на практике использовал теорему греческий философ Фалес Милетский. Он применил ее для измерения высоты пирамиды Хеопса, пользуясь падающей на песок тенью. Для сравнения длины отрезков использовалась воткнутая рядом палка.
Но доказательство теоремы, самое давнее из известных, зафиксированных в письменных источниках, дано в книге «Элементы» другого философа и математика — Эвклида. Тем не менее, утверждение получило имя Фалеса, под которым известно до сих пор.
Видео:Теорема фалеса. Теорема о пропорциональных отрезках - геометрия 8 классСкачать
Подобие треугольников и пропорциональные отрезки
Теорема 1:
Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.
Доказательство:
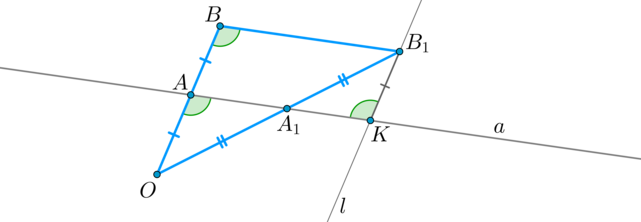
Докажем сначала лемму: Если в (triangle OBB_1) через середину (A) стороны (OB) проведена прямая (aparallel BB_1) , то она пересечет сторону (OB_1) также в середине.
Через точку (B_1) проведем (lparallel OB) . Пусть (lcap a=K) . Тогда (ABB_1K) — параллелограмм, следовательно, (B_1K=AB=OA) и (angle A_1KB_1=angle ABB_1=angle OAA_1) . Значит, по второму признаку (triangle OAA_1=triangle B_1KA_1 Rightarrow OA_1=A_1B_1) . Лемма доказана.
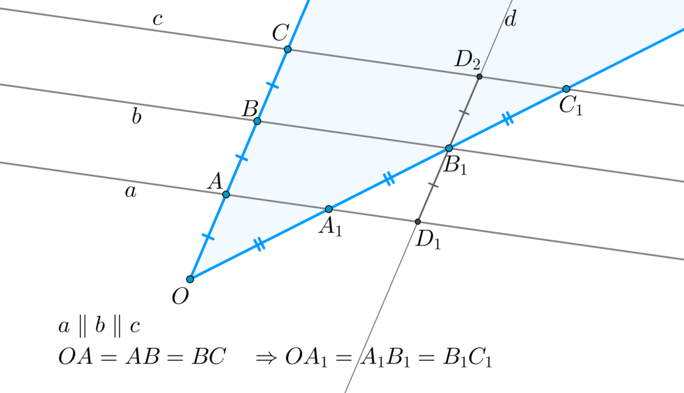
Перейдем к доказательству теоремы. Пусть (OA=AB=BC) , (aparallel bparallel c) и нужно доказать, что (OA_1=A_1B_1=B_1C_1) .
Таким образом, по данной лемме (OA_1=A_1B_1) . Докажем, что (A_1B_1=B_1C_1) . Проведем через точку (B_1) прямую (dparallel OC) , причем пусть (dcap a=D_1, dcap c=D_2) . Тогда (ABB_1D_1, BCD_2B_1) — параллелограммы, следовательно, (D_1B_1=AB=BC=B_1D_2) . Значит, по первому признаку (triangle A_1B_1D_1=triangle C_1B_1D_2 Rightarrow A_1B_1=B_1C_1) .
Теорема Фалеса:
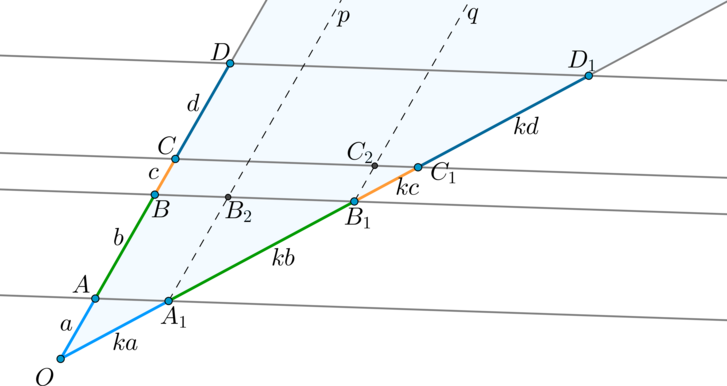
Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.
Доказательство:
Пусть параллельные прямые (pparallel qparallel rparallel s) разбили одну из прямых на отрезки (a, b, c, d) . Тогда вторую прямую эти прямые должны разбить на отрезки (ka, kb, kc, kd) соответственно.
Проведем через точку (A_1) прямую (pparallel OD) ( (ABB_2A_1) — параллелограмм, следовательно, (AB=A_1B_2) ). Тогда (triangle OAA_1 sim triangle A_1B_1B_2) по двум углам. Следовательно, (dfrac=dfrac Rightarrow A_1B_1=kb) .
Аналогично проведем через (B_1) прямую (qparallel OD Rightarrow triangle OBB_1sim triangle B_1C_1C_2 Rightarrow B_1C_1=kc) и т.д.
Наиболее часто встречающиеся подобия треугольников:
Теорема 2.
Средняя линия треугольника отсекает от него подобный ему треугольник.
Доказательство:
Т.к. средняя линия — это отрезок, соединяющий середины двух сторон, то (dfrac=dfrac=2) .
Таким образом, по двум пропорциональным сторонам и углу между ними ( (angle B) — общий) (triangle A_1BC_1 sim triangle ABC) .
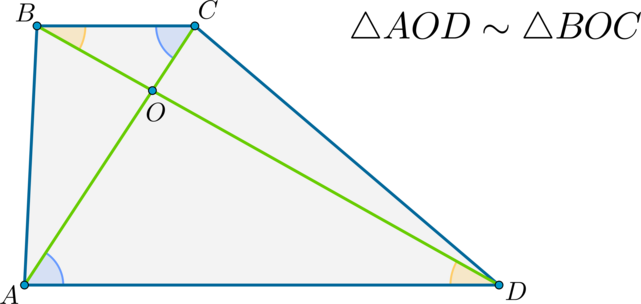
Теорема 3.
Треугольники, образованные диагоналями трапеции и основаниями, подобны.
Доказательство:
Т.к. (ADparallel BC Rightarrow angle OBC=angle ODA) . (angle BOC=angle AOD) как вертикальные. Следовательно, по двум углам (triangle BOCsim triangle AOD) .
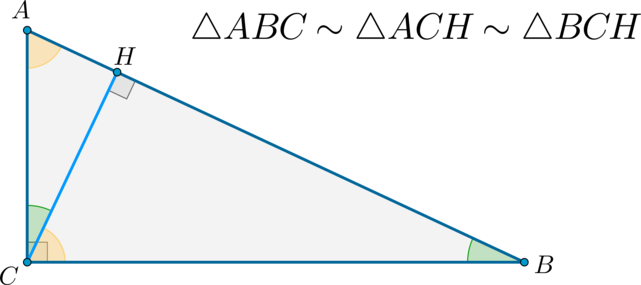
Теорема 4.
Высота прямоугольного треугольника, проведенная к гипотенузе, делит его на два подобных треугольника.
Доказательство:
Обозначим (angle ACH=alpha, angle BCH=beta) , т.е. (alpha+beta=90^circ) . Тогда (angle CAH=90^circ-alpha=beta, angle CBH=90^circ-beta=alpha) .
Следовательно, по двум углам (triangle ACHsim triangle BCHsim ABC) .
Теорема 5.
Отрезки, соединяющие основания высот треугольника, отсекают от него подобные ему треугольники.
Эти отрезки также являются биссектрисами углов треугольника, вершинами которого являются основания данных высот.
Доказательство:
1) Рассмотрим четырехугольник (AC_1A_1C) — около него можно описать окружность, т.к. (angle AC_1C=angle AA_1C) . Таким образом, (angle CAA_1=angle CC_1A_1=x) , т.к. опираются на одну и ту же хорду (A_1C) . Таким образом (angle ACA_1=90^circ-x, angle BC_1A_1=90^circ-x Rightarrow angle ACA_1=angle BC_1A_1) .
Значит, по двум углам (triangle A_1BC_1sim triangle ABC) ( (angle B) — общий).
Аналогично доказывается, что (triangle AB_1C_1sim triangle ABC, triangle A_1B_1Csim triangle ABC) .
2) Докажем, что (AA_1, BB_1, CC_1) – биссектрисы углов (A_1, B_1, C_1) в треугольнике (A_1B_1C_1) соответственно.
Обозначим (angle BC_1A_1=angle B_1C_1A=alpha) . Тогда (angle A_1C_1C=90^circ -alpha=angle B_1C_1C) . Значит, (CC_1) – биссектриса угла (C_1) .
Аналогично доказывается про (AA_1) и (BB_1) .
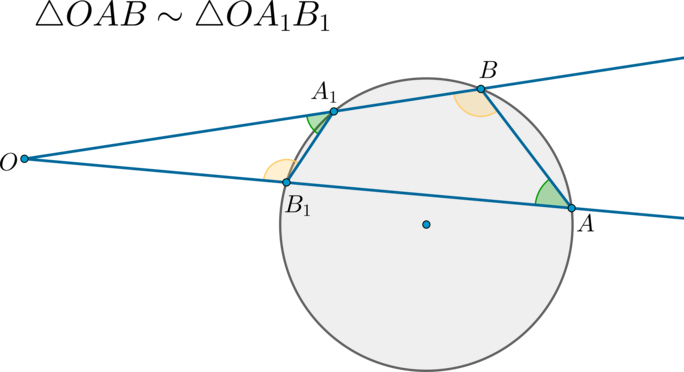
Теорема 6.
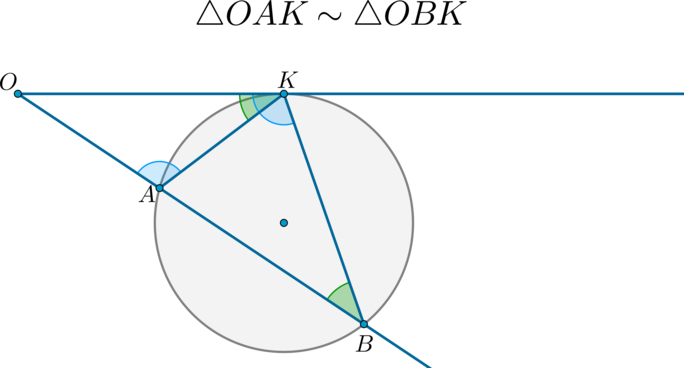
Если к окружности из одной точки вне окружности проведены две секущие, то:
Доказательство:
Четырехугольник (ABA_1B_1) описанный, следовательно, (angle BAB_1+angle BA_1B_1=180^circ Rightarrow angle OA_1B_1=180^circ-angle BA_1B_1=angle BAB_1) .
Таким образом, по двум углам ( (angle O) — общий) (triangle OABsim triangle OA_1B_1) .
Теорема 7.
Если к окружности из одной точки проведены касательная и секущая, то:
Доказательство:
Т.к. угол между касательной и хордой, проведенной в точку касания, равен половине дуги, заключенной между ними, то (angle OKA=frac12 buildrelsmileover=angle KBA) .
Следовательно, по двум углам ( (angle O) — общий) (triangle OKAsim triangle OKB) .
Теорема 8.
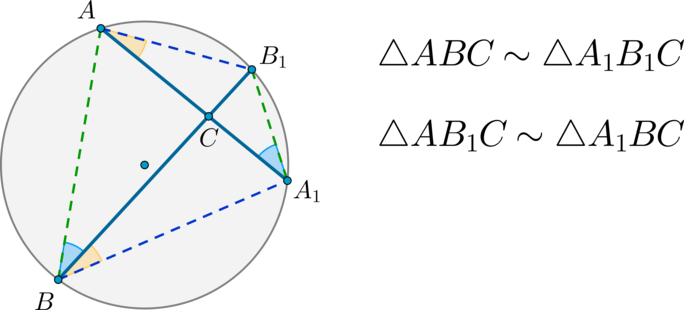
Если в окружности две хорды пересекаются, то:
Доказательство:
(angle A_1AB_1=angle A_1BB_1) , т.к. опираются на одну и ту же дугу. (angle A_1CB=angle B_1CA) , т.к. они вертикальные. Следовательно, по двум углам (triangle A_1BCsim triangle B_1C) .
Аналогично (triangle ABCsim triangle A_1B_1C) .
🎥 Видео
Пропорциональные отрезки. Медианы в треугольнике. Теорема Фалеса. Задачи для ОГЭ и ЕГЭ.Скачать

Пропорциональные отрезкиСкачать

Пропорциональные отрезки | Геометрия 7-9 класс #56 | ИнфоурокСкачать

Геометрия 8. Урок 8 - Теорема Фалеса - теорияСкачать

ТЕОРЕМА ФАЛЕСА . §11 геометрия 8 классСкачать

Теорема о пропорциональных отрезках. Теорема ФалесаСкачать

Пропорциональные отрезки круга. 9 класс.Скачать

Теорема о пропорциональных отрезкахСкачать

8 класс, 26 урок, Пропорциональные отрезки в прямоугольном треугольникеСкачать

Геометрия. 8 класс. Теорема Фалеса. Пропорциональные отрезки /06.10.2020/Скачать

Теорема Фалеса. Теорема о пропорциональных отрезках. Экстра Математика ЕГЭСкачать

58. Пропорциональные отрезкиСкачать