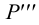§ 12. Параллельное проектирование и его свойства.
В начале учебника на плоскости изображены некоторые фигуры, расположенные в пространстве. Эти изображения строились с целью придать наглядность тому, о чём шла речь в соответствующей теореме или задаче.
Однако изображения пространственных фигур на плоскости строятся по определённым правилам и в школьном курсе геометрии обычно осуществляются с помощью метода параллельного проектирования, сущность которого состоит в следующем.
В пространстве выбирается произвольная плоскость π Плоскость проекций в начертательной геометрии чаще всего обозначают π . , которую называют плоскостью проекций или плоскостью изображения , и прямая l , пересекающая эту плоскость (рис. 71, а ).
Пусть M ′ — произвольная точка пространства. Через эту точку проведём прямую p , параллельную l . Точка M пересечения прямой p с плоскостью π называется параллельной проекцией точки M ′ на плоскость π в направлении прямой l . Если M ′ — точка плоскости π , то M совпадает с M ′ .
При этом часто пользуются обозначением: M = П 
Прямую l и все прямые пространства, параллельные ей, называют проектирующими прямыми ; они определяют направление проектирования. Всякая плоскость пространства, параллельная проектирующей прямой, называется проектирующей плоскостью .
Фигура, которую проектируют или изображают, называется оригиналом. Для построения проекции фигуры достаточно построить проекции всех точек этой фигуры или проекции точек фигуры, её определяющих. На рисунке 71, б треугольник ABC является параллельной проекцией треугольника A ′ B ′ C ′ на плоскость π в направлении прямой l .
Замечание. Наряду с параллельным проектированием рассматривается также центральное проектирование фигур на плоскость. В этом случае проектирующие прямые проходят через одну точку — центр проектирования , произвольно выбранную вне плоскости проекций (рис. 71, в ).
Параллельное и центральное проектирование можно наблюдать в реальном пространстве: тень, которую отбрасывает предмет в солнечный день, является параллельной проекцией этого предмета, так как солнечные лучи можно считать приближённо параллельными вследствие большого удаления Солнца от Земли. А изображение на экране кинотеатра фигуры, заснятой на киноплёнку, является центральной проекцией этой фигуры.
На рисунках 72, 73, 74 изображены в параллельной проекции соответственно квадрат, треугольник и каркас тетраэдра. По этим рисункам можно сделать предположение, что ни величина угла, ни длина отрезка при параллельном проектировании, вообще говоря, не сохраняются.
Рассмотрим некоторые свойства параллельного проектирования.
1. Все точки проектирующей прямой проектируются в одну точку — точку пересечения этой прямой с плоскостью проекций (рис. 75).
В дальнейшем мы будем рассматривать проекции прямых, не параллельных проектирующим прямым.
2. Проекция прямой есть прямая. Действительно, все прямые, проектирующие точки данной прямой m ′ (рис. 76), принадлежат некоторой проектирующей плоскости, которая пересекает плоскость проекций по некоторой прямой m — параллельной проекции прямой m ′ .
Причём, так как через точку, не лежащую на данной прямой, можно провести лишь одну прямую, параллельную этой прямой (т. 6) (мы проводим прямые, параллельные прямой l ), то каждая точка прямой m ′ проектируется в единственную точку своей проекции — прямой m , и наоборот, каждая точка прямой m является проекцией единственной точки прямой m ′ .
Из доказательства этого свойства следует: три точки, лежащие на одной прямой, проектируются в три точки, также лежащие на одной прямой .

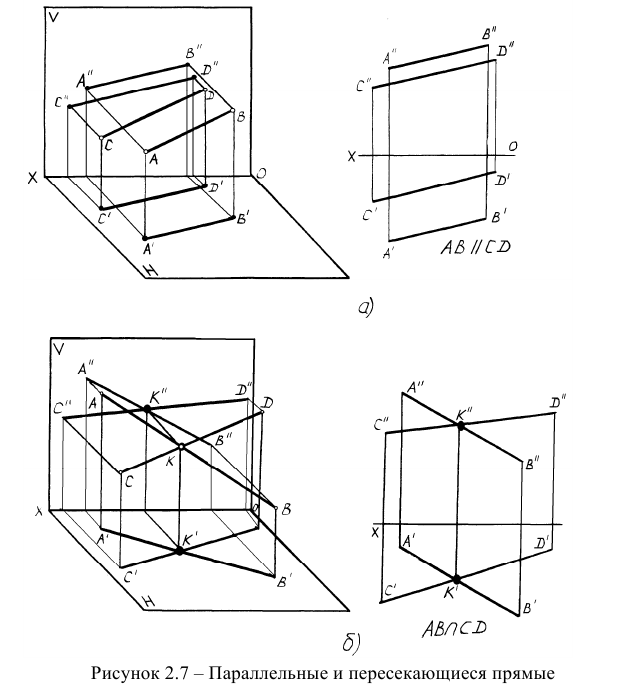
3. Две параллельные прямые проектируются либо в две параллельные прямые, либо в одну и ту же прямую. Действительно, если прямые a ′ и b ′ лежат в одной проектирующей плоскости, то они проектируются в одну и ту же прямую, а именно, в прямую, по которой эта проектирующая плоскость пересекает плоскость проекций.
Пусть теперь прямые a ′ и b ′ параллельны (рис. 77) и не лежат в одной проектирующей плоскости.
Обозначим через α и β плоскости, образованные прямыми, проектирующими точки прямых соответственно a ′ и b ′ . Прямые a и b , по которым плоскости α и β пересекают плоскость проекции, не могут пересекаться, так как если бы эти прямые имели общую точку M , то и прямые a ′ и b ′ по свойству 2 имели бы общую точку M ′ , что невозможно в силу параллельности прямых a ′ и b ′ . А так как прямые a и b лежат в одной плоскости (плоскости проекций) и не имеют общей точки, то они параллельны, т. е. параллельными проекциями параллельных прямых, не лежащих в одной проектирующей плоскости, являются параллельные прямые.
Заметим, что плоскости α и β , проектирующие параллельные прямые a ′ и b ′ , не лежащие в одной проектирующей плоскости, параллельны (в п. 9.1 показано, что параллельные плоскости существуют; о свойствах параллельных плоскостей речь пойдёт в следующей главе).
4. Проекции параллельных отрезков лежат либо на параллельных прямых, либо на одной прямой. Отношение длин отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин проекций этих отрезков.
Если отрезки A ′ B ′ и B ′ C ′ лежат на одной прямой a ′ и проектируются на отрезки соответственно AB и BC прямой a (рис. 78), то по обобщённой теореме Фалеса в плоскости, определяемой прямыми a и a ′ , получаем A ′ B ′ : B ′ C ′ = AB : BC = m : n .
Пусть теперь отрезки A ′ B ′ и C ′ D ′ расположены соответственно на данных параллельных прямых a ′ и b ′ , не лежащих в одной проектирующей плоскости, и A ′ B ′ : C ′ D ′ = m : n ; AB и CD , a и b — соответственно их параллельные проекции на плоскость π (рис. 79).
Так как a ′ ‖ b ′ , то (по свойству 3) a ‖ b . Пусть E — такая точка прямой a , что четырёхугольник BCDE — параллелограмм. Тогда на прямой a ′ существует (единственная!) такая точка E ′ , что E ′ E ‖ DD ′ и A ′ B ′ : B ′ E ′ = AB : BE . А так как BC ‖ ED , то B ′ C ′ ‖ E ′ D ′ (по свойству 3), значит, B ′ C ′ D ′ E ′ — параллелограмм. Поэтому A ′ B ′ : C ′ D ′ = A ′ B ′ : B ′ E ′ = AB : BE = AB : CD , т. е. A ′ B ′ : C ′ D ′ = AB : CD = m : n .
Из этого свойства, очень важного для теории построений изображений пространственных фигур на плоскости, следует не менее важный вывод: если отрезок A ′ C ′ параллельно проектируется на отрезок AC и точка B ′ делит отрезок A ′ C ′ в отношении A ′ B ′ : B ′ C ′ = m : n , то точка B — проекция точки B ′ — делит отрезок AC в том же отношении m : n , т. е. AB : BC = A ′ B ′ : B ′ C ′ = m : n . В частности, середина отрезка A ′ C ′ параллельно проектируется в середину отрезка AC ( m : n = 1 : 1) (рис. 80).
Пусть M — внутренняя точка отрезка AB .
Определение. Число λ , равное отношению длин отрезков AM и MB , на которые точка M делит отрезок AB , называется простым отношением трёх точек A , B и M , лежащих на одной прямой, и обозначается ( AB ; M ), т. е. ( AB ; M ) = λ = AM : MB .
При этом точки A и B называются базисными , а точка M — делящей точкой.
Упорядоченность точек простого отношения необходима. Например, если AA 1 — медиана треугольника ABC , M — его центроид (точка пересечения медиан треугольника), то ( AA 1 ; M ) = AM : MA 1 = 2 : 1, но ( A 1 A ; M ) = A 1 M : MA = 1 : 2 (рис. 81). Поэтому, если AM ≠ MA 1 , то
( AA 1 ; M ) ≠ ( A 1 A ; M ).
Учитывая свойство 4 параллельного проектирования, можно сделать вывод: простое отношение трёх точек, лежащих на одной прямой, при параллельном проектировании сохраняется . В этом случае также говорят, что простое отношение трёх точек, лежащих на одной прямой, — инвариант параллельного проектирования .
Свойства фигуры, сохраняющиеся при параллельном проектировании, называются аффинными свойствами этой фигуры. Например, свойства прямых быть параллельными — аффинное свойство этих прямых; инвариантность простого отношения трёх точек одной прямой — аффинное свойство таких точек.
Подробнее о параллельном проектировании и изображениях фигур на плоскости читайте в конце учебника.
Определение. Проектирование в направлении прямой, перпендикулярной плоскости проекций, называется ортогональным.
Удобно пользоваться обозначением: M = П 
Ортогональное проектирование является частным случаем параллельного и обладает всеми его свойствами. Однако, если при параллельном проектировании, не являющимся ортогональным, длина проекции отрезка может быть меньше, больше или равна длине самого отрезка, то при ортогональном проектировании длина проекции отрезка не больше, чем длина самого отрезка, и длины этих отрезков связаны соотношением: П 
Задания для работы с интернет-ресурсами
1. Наберите в поисковой системе слова «Перпендикулярность прямой и плоскости», «Перпендикуляр и наклонная к плоскости», «Наклонная и её проекция на плоскость», «Теорема о трёх перпендикулярах». На изображениях куба, параллелепипеда найдите рёбра и диагонали, перпендикулярные граням и сечениям этих многогранников. Найдите видеоролики с лекциями опытных педагогов и геометров, в которых выражаются различные взгляды как на теорию, так и на решение задач по этим вопросам.
2. Наберите в поисковой системе слова «угол между наклонной и плоскостью». Поищите задачи ЕГЭ типа С-2, в которых используется нахождение угла между прямой и плоскостью, посмотрите, как они решаются, попробуйте решить их самостоятельно. Если вам удалось найти в Интернете тренинг по решению задач этой темы, то попытайтесь им воспользоваться. Однако решать такие задачи целесообразнее после изучения темы «Расстояния в пространстве». Скоро вы изучите эту тему.
3. Изображения фигур на плоскости и в живописи подчиняются определённым законам. Найдите в Интернете такие имена, как Филиппо Брунеллески (1377—1446), Леонардо да Винчи (1452—1519) и Альбрехт Дюрер (1471—1528). Вы увидите творчество этих великих художников. Однако существует направление, которое называется импоссибилизм (impossibility — невозможность) — изображение невозможных фигур, парадоксов. Представителем этого направления живописи является известный голландский художник Мауриц Эшер (1898—1972). Найдите статьи, посвящённые его творчеству, а главное, найдите сами репродукции картин, которые представляют большой интерес и с точки зрения геометрии.
- Чертежик
- Метки
- Взаимное расположение прямых линий
- Проецирование прямой линии в начертательной геометрии с примерами
- Прямые общего и частного положения
- Прямые, параллельные плоскостям проекций
- Прямые, перпендикулярные плоскостям проекций
- Определение натуральной величины прямой
- Следы прямой
- Взаимное положение прямых
- Образование проекций. Методы проецирования
- Ортогональный чертеж. Проецирование точки
- Октанты
- Проекции отрезка прямой линии. Точка на прямой
- Прямые частного положения
- Определение натуральной величины отрезка прямой общего положения методом прямоугольного треугольника
- Следы прямой
- Взаимное положение двух прямых
- Проецирование плоских углов
- 🔍 Видео
Видео:Параллельность прямых. 10 класс.Скачать

Чертежик
Метки
Видео:Параллельность прямой к плоскостиСкачать

Взаимное расположение прямых линий
Взаимное расположение прямых линий может быть представлено следующим образом: быть параллельными, пересекаться, скрещиваться.
1. Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек.
Проекции параллельных прямых на любую плоскость проекций (не перпендикулярную данным прямым) — параллельны.
- Пересекающимисяназываются две прямые лежащие в одной плоскости и имеющие одну общую точку.
Прямые пересекаются, если их одноименные проекции также пересекаются, а проекции точки пересечения лежат на одной линии связи.
- Скрещивающимисяназываются две прямые не лежащие в одной плоскости.
Прямые скрещиваются, если они не пересекаются и не параллельны между собой, а точки пересечения их одноименных проекций не лежат на одной линии связи.
Примеры выполненных чертежей смотрите в этом разделе .
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Проецирование прямой линии в начертательной геометрии с примерами
Содержание:
Проецирование прямой линии:
Отрезок прямой линии определяется двумя точками. Следовательно, проекции двух точек определяют проекции отрезка прямой (рисунок 2.1). Проекции отрезка прямой в общем случае всегда будут меньше самого отрезка прямой. В общем случае по проекциям отрезка прямой нельзя определить углы наклона отрезка прямой к плоскостям проекций.
Видео:Следы прямой Взаимное положение двух прямыхСкачать

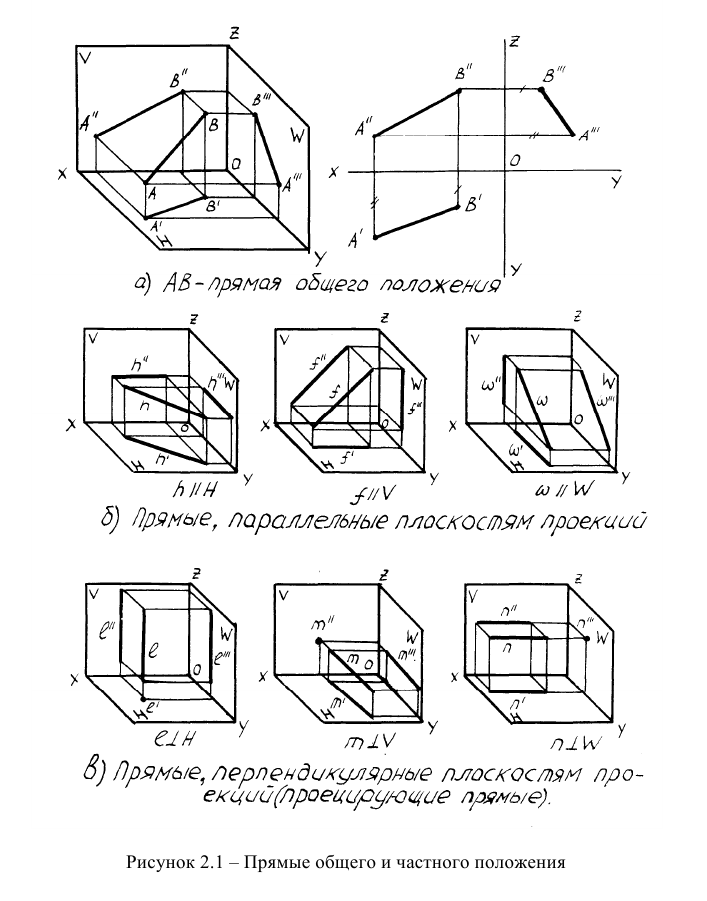
Прямые общего и частного положения
Прямые подразделяются на прямые общего и частного положения. Прямая, не параллельная и не перпендикулярная ни одной из плоскостей проекций, называется прямой общего положения (рисунок 2.1а).
Прямые, параллельные или перпендикулярные плоскостям проекций, называются прямыми частного положения (рисунок 2.16, в). Прямые, параллельные плоскостям проекций, называются по имени плоскости, которой они параллельны: горизонталь h, фронталь f и профильная прямая w.
Прямые, перпендикулярные плоскостям проекций, называются проецирующими: горизонтально-проецирующая, фронтально-проецирующая и профильно-проецирующая, в зависимости от плоскости, к которой они перпендикулярны.
Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Прямые, параллельные плоскостям проекций
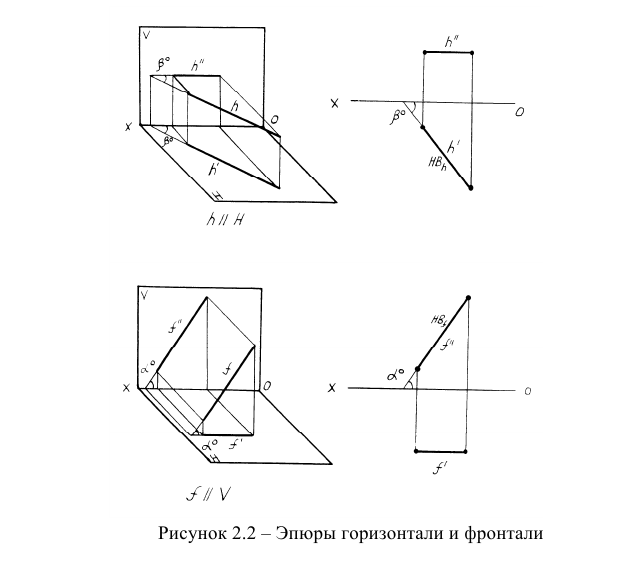
Особенностью эпюра прямых, параллельных плоскостям проекций, является то, что две проекции прямой параллельны осям, а третья проекция наклонена к осям и является натуральной величиной прямой.
Кроме того, по этой проекции прямой можно определить угол наклона прямой к той или иной плоскости проекций.
Среди упомянутых прямых особое место занимают горизонталь h и фронталь f (рисунок 2.2), которые обладают замечательными свойствами и поэтому часто применяются при решении различных задач.
Важнейшими свойствами горизонтали являются: фронтальная
проекция горизонтали
Видео:Математика это не ИсламСкачать

Прямые, перпендикулярные плоскостям проекций
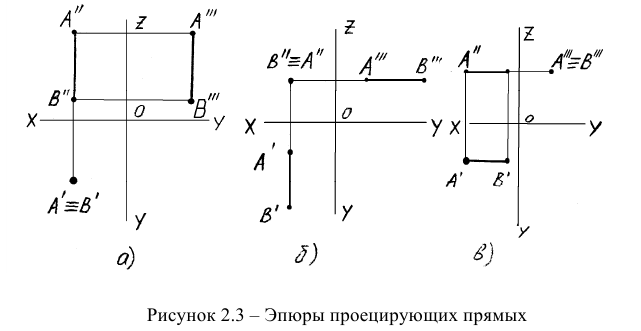
Особенностью эпюра прямых, перпендикулярных плоскостям проекций, является то, что две проекции этих прямых параллельны осям, а третья проекция «вырождается» в точку на той плоскости проекций, которой эта прямая перпендикулярна. Первые две проекции проецирующих прямых являются их натуральной величиной. На рисунке 2.3 представлены эпюры горизонтально- (а), фронтально- (б) и профильно-проецирующих прямых (в).
Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Определение натуральной величины прямой
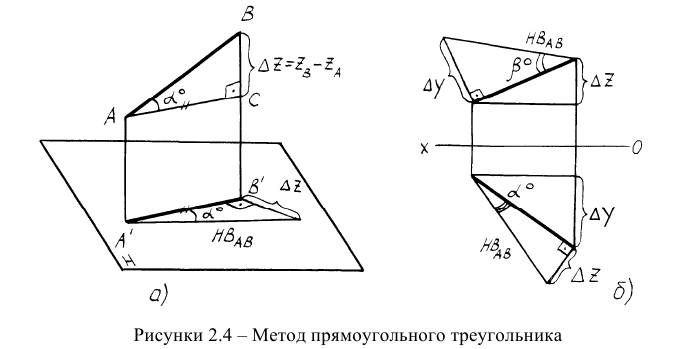
Так как прямая общего положения проецируется на плоскости проекций с искажением, то задача определения натуральной величины (НВ) прямой по её проекциям является важной. С целью определения НВ прямой разработан метод прямоугольного треугольника, сущность которого понятна из пространственного чертежа (рисунок 2.4а).
Для того, чтобы определить натуральную величину прямой по её проекциям, необходимо на одной из её проекций (на любой) построить прямоугольный треугольник, одним катетом которого является сама проекция, а другим катетом — разность недостающих координат концов отрезка прямой. Тогда гипотенуза треугольника будет являться НВ прямой (рисунок 2.46). Недостающей координатой здесь названа та координата, которая не участвует в построении той или иной проекции прямой. Так, например, горизонтальная проекция прямой строится по координатам X и Y её концов.
Координата Z в построениях не участвует и называется недостающей координатой. Таким образом, при построении прямоугольного треугольника на горизонтальной проекции прямой на катете откладывают разность аппликат, а при построении на фронтальной проекции — разность ординат.
При определении НВ прямой методом прямоугольного треугольника одновременно можно определить углы наклона прямой к плоскостям проекций (углы а° и 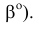
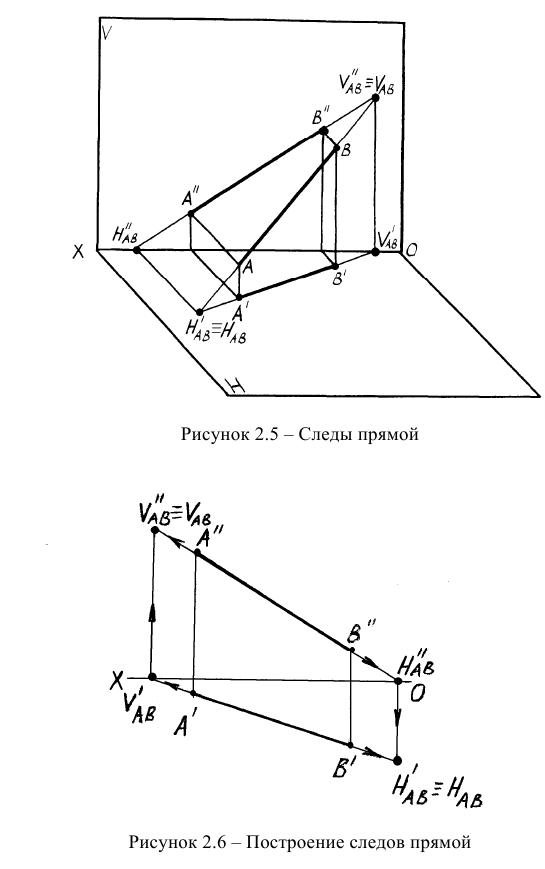
Следы прямой
Точки пересечения прямой с плоскостями проекций называются следами прямой. В точках следов прямая переходит из одного октанта в другой. Различают горизонтальный, фронтальный и профильный следы прямой и их соответствующие проекции. На рисунке 2.5 показаны пространственные чертежи прямых общего и частного положения и образование их следов. Прямые, параллельные плоскостям проекций, имеют только два следа, а прямые, перпендикулярные плоскостям проекций, — один след, совпадающий с той проекцией прямой, на которой она проецируется в точку.
Из пространственных чертежей следует методика построения проекций следов прямой на эпюре (рисунок 2.6).
Взаимное положение прямых
Прямые в пространстве могут быть параллельными, пересекающимися, скрещивающимися и перпендикулярными.
Пространственные чертежи и эпюры параллельных и пересекающихся прямых представлены на рисунке 2.7а, б.
Признаком параллельных прямых на эпюре является параллельность их одноименных проекций.
Пересекающимися прямыми называются прямые, которые имеют общую точку — точку пересечения. Признаком пересекающихся прямых на эпюре является то, что проекции точки пересечения находятся на одной линии связи.
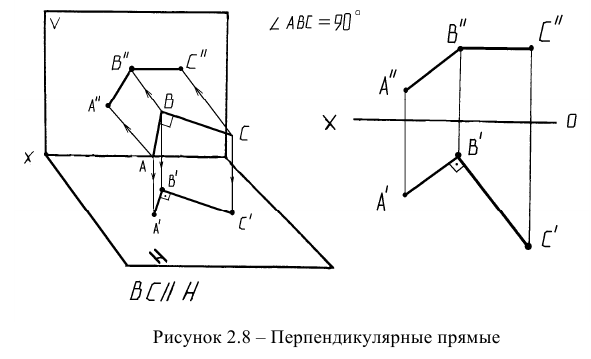
Частным случаем пересекающихся прямых являются перпендикулярные прямые. В соответствии с теоремой о проецировании прямого угла, прямой угол будет проецироваться на плоскость проекций в натуральную величину в том случае, когда одна из его сторон будет параллельна этой плоскости проекций (Рисунок 2.8).
Cкрещивающимися прямыми называются непараллельные прямые, не имеющие общей точки. Скрещивающиеся прямые в пространстве не пересекаются, но на эпюре их одноименные проекции накладываются друг на друга, что создает впечатление пересечения. Признаком скрещивающихся прямых на проекциях является то, что проекции их мнимых точек пересечения не находятся на одной линии связи (рисунок 2.9а). В мнимых точках пересечения конкурируют две точки, принадлежащие разным прямым, или, другими словами, в мнимых точках конкурируют две прямые. Назовем эту область конкурирующим местом.
При рассмотрении скрещивающихся прямых возникает вопрос о видимости проекций прямых в конкурирующих местах. Этот вопрос может быть решен методом конкурирующих точек (конкурирующих прямых).
Сущность метода заключается в следующем:
- Отметить конкурирующее место на рассматриваемой проекции;
- Обозначить конкурирующие точки или записать, какие прямые конкурируют;
- Провести через конкурирующее место линию связи;
- Вдоль линии связи сравнить недостающие координаты конкурирующих точек или конкурирующих прямых;
- На рассматриваемой проекции будет видна та точка или прямая, которая имеет наибольшую недостающую координату.
Так на рисунке 2.96 на горизонтальной проекции будет видна точка 1, принадлежащая прямой AВ, или, проще говоря, прямая АВ, так как аппликата прямой АВ вдоль линии связи наибольшая. На фронтальной проекции также будет видна прямая AВ. так как у неё в конкурирующем месте наибольшая ордината.
Метод конкурирующих точек (прямых) используется и при определении видимости проекций прямой и плоскости, двух плоскостей, прямой и поверхности, ребер многогранников и т.д. При этом считается, что плоскости и поверхности геометрически непрозрачны, а видимость прямой в точке встречи с плоскостью или в точках встречи с поверхностью меняется.
На рисунке 2.10 представлена пространственная схема определения видимости проекций прямой MN и плоскости ABCD, пересекающихся друг с другом в точке К. На горизонтальной проекции в конкурирующем месте будет видна прямая ВС, так как её аппликата больше, чем у прямой MN. На фронтальной проекции в конкурирующем месте будет видна прямая MN, так как ордината у неё больше, чем у прямой АВ.
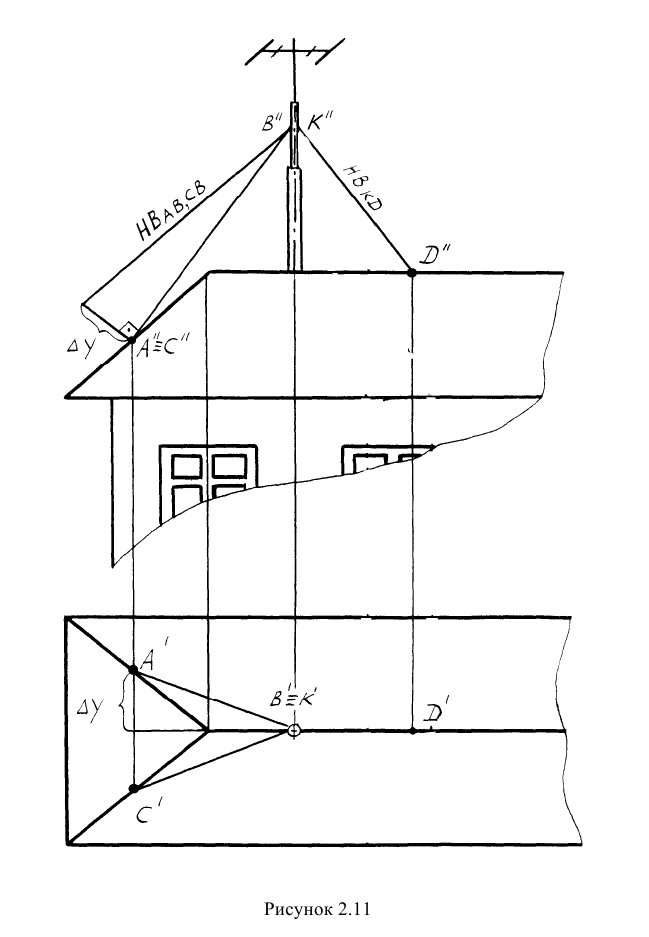
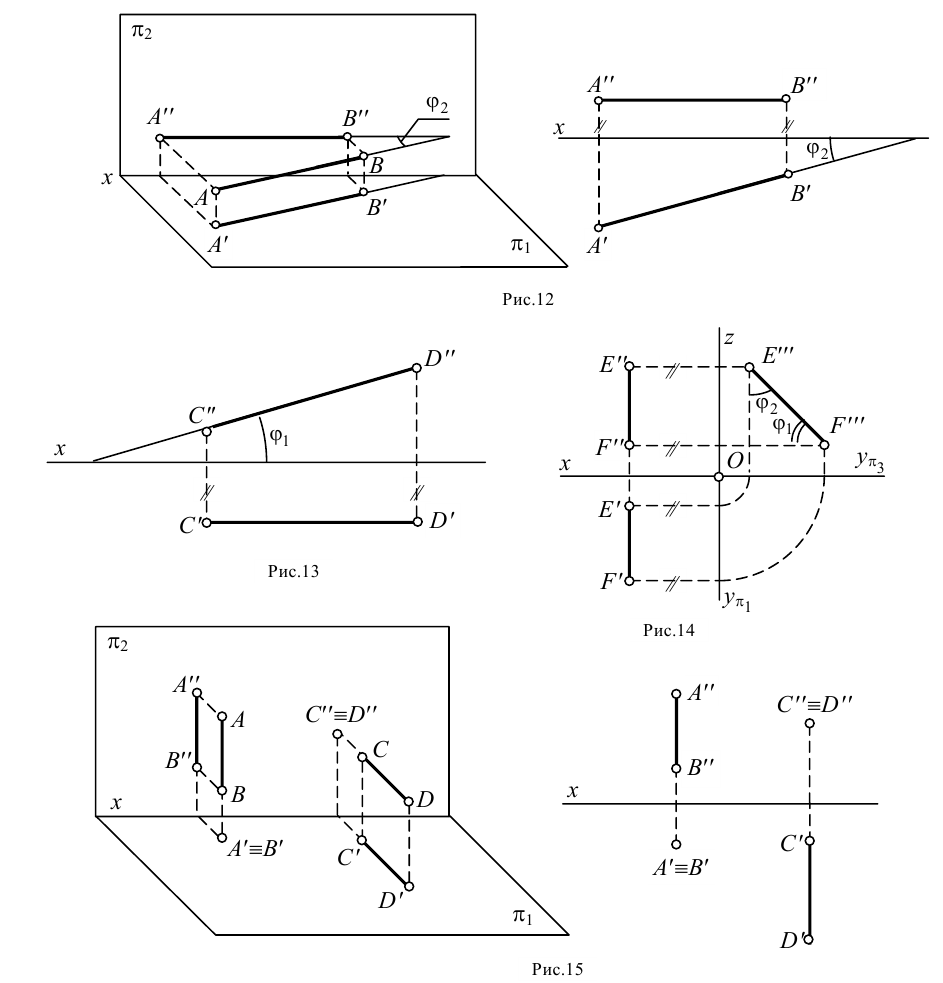
Пример: Определить длину растяжек для крепления антенны к крыше здания (рисунок 2.11).
Решение: Длина растяжек АВ и ВС определена методом прямоугольного треугольника на фронтальной проекции. Длину растяжки KD определять не следует, так как прямая KD является фронталью и её фронтальная проекция 
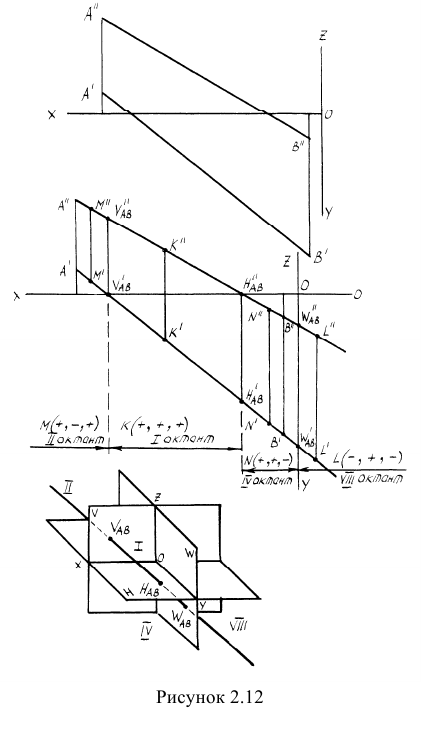
Пример: Построить следы прямой АВ и определить октанты, через которые проходит прямая (рисунок 2.12).
Решение: Задача решена в пространстве и на эпюре. Так как проекции прямой пересекают оси ОХ и 0Y, то в точках пересечения и будут находится проекции горизонтального, фронтального и профильного следов прямой. Далее по знакам координат точек М, К, N, L определяем, что прямая проходит через октанты ll, I, IV и VIII.
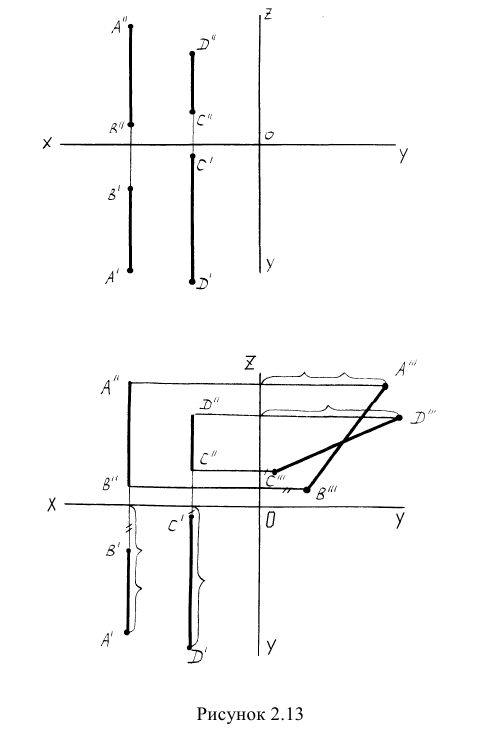
Пример: Определить взаимное положение прямых АВ и CD (рисунок 2.13).
Решение: Анализ проекций двух заданных прямых приводит к выводу, что они являются профильными прямыми, так как обе их проекции параллельны осям 0Y и 0Z. Анализ взаимной параллельности одноименных проекций позволяет сделать предварительный вывод о том, что прямые АВ и CD параллельны друг другу. Однако такой вывод неправомерен, так как для профильных прямых следует проверить параллельность на профильной проекции. Построив профильные проекции 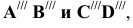
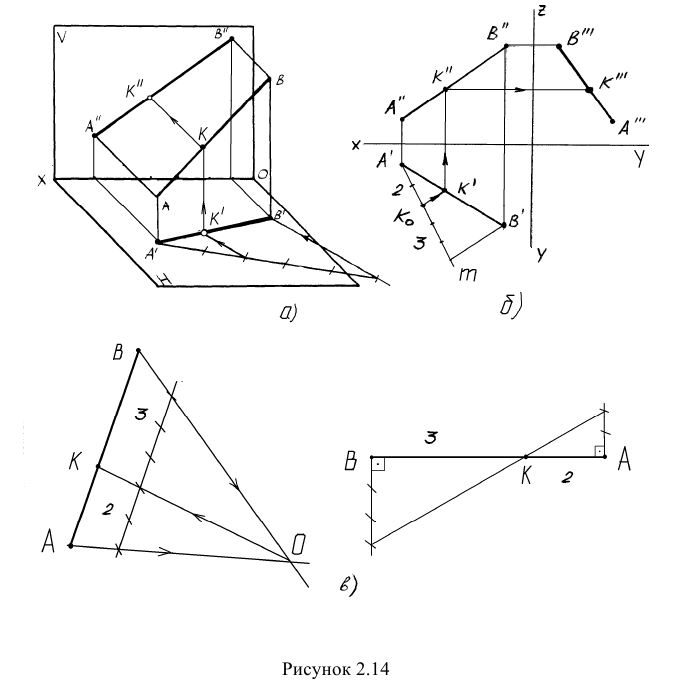
Пример: Разделить отрезок прямой АВ в отношении 2:3 (рисунок 2.14а).
Решение: Так как отношение отрезков прямой линии равно отношению их проекций, то разделить в данном отношении отрезок прямой на эпюре — значит разделить в том же отношении любую его проекцию.
Задача решается исключительно графическим методом. Представленное решение задачи основано на теореме Фалеса: если на одной стороне угла отложить равные или пропорциональные отрезки и провести через засечки любые параллельные прямые, то другая сторона разделится на равные или пропорциональные отрезки. На рисунке 2.14а дано решение задачи в пространственной форме, а на рисунке 2.146 представлен эпюр решения задачи. На горизонтальной проекции вспомогательная прямая m проводится под произвольно углом, и на ней откладывается пять произвольных отрезков равной длины.
На рисунке 2.14в представлены ещё два способа деления отрезка прямой в заданном отношении.
Изготовление любой детали, строительство сооружений, разработка месторождений полезных ископаемых начинается с составления чертежей, планов и схем. Никакие словесные описания не могут заменить чертеж, который позволяет не только определить форму и размеры всех частей предмета, но и получить наглядное представление о нем.
Начертательная геометрия — один из разделов геометрии, в котором свойства пространственных фигур изучают по их изображениям на той или иной поверхности. Чаще всего за такую поверхность принимают плоскость.
Как и любая научная дисциплина, начертательная геометрия имеет терминологию, которую следует хорошо усвоить, чтобы понимать излагаемый материал.
В геометрии вообще и в начертательной геометрии в частности каждое последующее изложение основывается на предыдущем материале. Такая особенность изучаемого предмета требует систематической, последовательной работы над ним.
Потребность в отображении действительности появилась у человека давно. Об этом свидетельствуют многочисленные изображения первобытного человека на стенах пещер и камнях, на предметах и орудиях труда. С развитием человечества совершенствовалась и техника передачи различных символов (письменность, схемы, чертежи). В Древнем Китае, например, была разработана всеобъемлющая знаковая система, где каждому предмету или явлению соответствовал особый знак (иероглиф). В Древнем Египте при возведении сооружений архитекторы использовали чертежи в виде планов и фасадов.
Основные правила и методы построения изображений (планов зданий, земельных угодий, крепостных укреплений) по законам геометрии были разработаны в эпоху античности. В Древней Греции, за 300 лет до нашей эры, сделаны первые шаги к научному обоснованию метода центрального проецирования. В «Оптике» Евклида содержатся 12 аксиом и 61 теорема об условиях «видения» предметов.
Расцвет классической культуры сменился застоем, и только в эпоху Возрождения, благодаря усилиям школ живописи и архитектуры Италии, Нидерландов и Германии, в истории начертательной геометрии начинается новый период развития. К этому времени относится введение целого ряда основных понятий метода проецирования.
С развитием архитектуры, машинного производства, горной промышленности к изображениям предметов стали предъявлять все более высокие требования, что и привело к необходимости обобщения и систематизации знаний по «теории изображений». Работа знаменитого французского геометра и инженера периода Великой французской революции Гаспара Монжа (1746-1818) «Geometrie Descriptive» (1798 г.) представляет собой первое систематическое изложение общего метода изображения пространственных фигур на плоскости, поднявшее начертательную геометрию на уровень самостоятельной научной дисциплины.
Преподавание начертательной геометрии в России началось уже в первые годы XIX в. в Корпусе инженеров путей сообщения и чуть позже в Горном кадетском корпусе. Первый русский профессор начертательной геометрии Я.И. Севастьянов (1796-1849) в 1821 г. составил курс «Основания начертательной геометрии», ставший классическим учебным пособием по этому предмету.
Среди ученых, внесших наиболее значительный вклад в развитие начертательной геометрии, следует отметить академика Е.С. Федорова (1853-1919), преподававшего в Горном институте. На примере решения задач минералогии и кристаллографии он показал применимость методов начертательной геометрии к исследованиям закономерностей материального мира.
В настоящее время начертательная геометрия является базовой общетехнической дисциплиной, составляющей основу инженерного образования. Было бы, однако, большой ошибкой ограничивать значение начертательной геометрии лишь рамками теоретической основы черчения. Ее методы дают возможность решать самые сложные проблемы в различных областях: горно-геологических науках, химии, физике и др.
Видео:Параллельные прямые циркулемСкачать

Образование проекций. Методы проецирования
В начертательной геометрии чертеж — основной инструмент решения различных пространственных задач. К выполняемому чертежу предъявляется ряд особых требований, четыре из которых являются наиболее существенными. Чертеж должен быть: 1) наглядным; 2) обратимым; 3) достаточно простым; 4) точным.
Остановимся более подробно на обратимости чертежа. Под этим свойством понимается возможность точного воспроизведения формы и размеров предмета по его изображению. Действительно, для всех видов технических и горно-геологических чертежей это требование является особенно важным, так как по чертежу в машиностроении изготавливается та или иная деталь, в горном деле осуществляется проходка горных выработок, в геологии — оценка запасов полезного ископаемого и т.д.
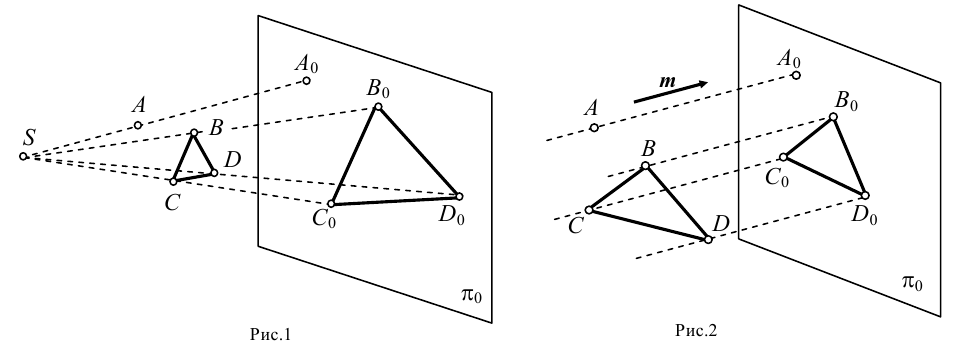
Основным методом получения изображений в начертательной геометрии является проецирование. Чтобы понять сущность проецирования, обратимся к рис.1.
Выбираем центр проецирования — произвольную точку 
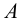
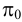
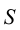
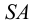
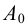
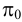
При этом точка 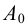
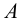
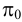
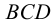
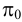
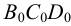
Если проецирование осуществляется из бесконечно удаленной точки пространства (рис.2), то все проецирующие прямые окажутся взаимно параллельными. Этот метод проецирования называется параллельным, а направление 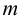
Если направление параллельного проецирования перпендикулярно плоскости проекций, то проецирование называется прямоугольным или ортогональным. Во всех остальных случаях параллельное проецирование называется косоугольным.
Изображения, полученные при помощи центрального проецирования, отличаются хорошей наглядностью, что объясняется устройством зрительного аппарата человеческого глаза. Однако этот метод имеет существенные недостатки. Во-первых, сложно построить изображение предмета. Во-вторых, построенные проекции имеют низкие метрические свойства, поэтому вследствие значительных искажений, возникающих при данном методе проецирования, определить истинные размеры предмета весьма сложно. По этим причинам способ центрального проецирования имеет ограниченное применение в практике и используется, когда от чертежа требуется прежде всего наглядность.
Несмотря на то, что параллельное проецирование, по сравнению с центральным, имеет меньшую наглядность, параллельные проекции, особенно ортогональные, обладают лучшей измеримостью и простотой построения.
Задачи, решаемые методами начертательной геометрии, принято делить на метрические и позиционные.
Метрические задачи имеют целью определение размеров различных предметов по их изображению. К таким задачам относится определение натуральной величины геометрических фигур, расстояний и углов между ними; в горно-геологической практике — это задачи на определение глубины и угла наклона буровых скважин, угла падения пласта полезного ископаемого, углов между осями горных выработок и т.п.
Позиционные задачи позволяют определить взаимное расположение различных объектов: точек, прямых линий, плоскостей, пространственных фигур. К этой категории задач относятся, например, установление точки встречи буровой скважины с плоскостью залежи, построение линии пересечения кровли и подошвы пласта полезного ископаемого с горной выработкой и многие другие.
Для быстрого и удобного решения пространственных задач в начертательной геометрии используют несколько систем изображений, особенности которых приведены в табл.1.
Таблица 1
Основные системы изображения, используемые при проецировании
Область применения той или иной системы изображений зависит, прежде всего, от целей, которые ставятся при построении чертежа. Из представленных в табл.1 систем наиболее широкое применение в техническом проектировании имеет эпюр (ортогональный чертеж). На его основе выполняются рабочие и сборочные чертежи, эскизы деталей, схемы и т.д. Поэтому в дальнейшем изложении курса основное внимание будет уделено именно этому методу построения.
Однако и другие методы проецирования находят применение в горно-геологических работах, поэтому в заключительных разделах будут рассмотрены основные правила изображения предметов при помощи векторных проекций, перспективы, аксонометрической проекции и, более подробно, — проекций с числовыми отметками.
Ортогональный чертеж. Проецирование точки
Любой предмет пространства можно рассматривать как определенную совокупность отдельных точек этого пространства, поэтому для изображения различных предметов необходимо научиться строить изображения отдельной точки пространства.
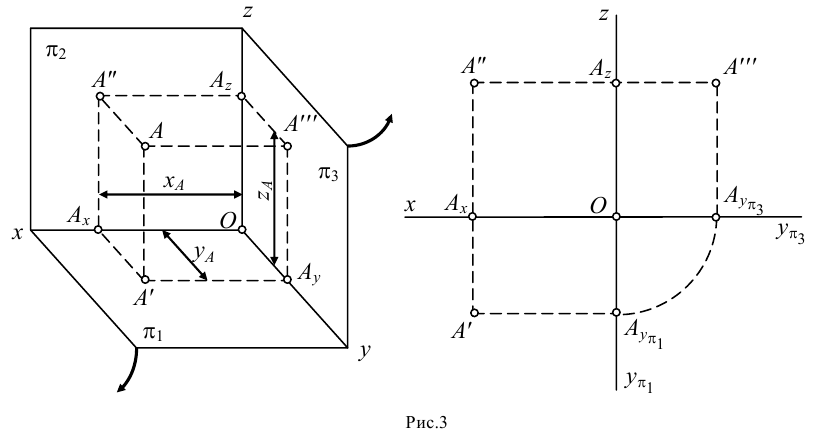
Представим в пространстве три взаимно перпендикулярные плоскости (рис.3):
— горизонтальную плоскость проекций;
— фронтальную плоскость проекций;
— профильную плоскость проекций.
Для наглядного изображения плоскостей проекций взята кабинетная проекция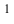
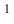
Плоскости проекций пересекаются по прямым, которые называются осями проекций и обозначаются 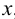
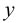
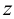
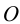
Представим себе также в пространстве некоторую точку 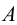
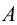
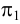
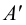
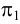
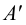
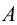
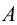
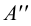
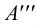
Длины отрезков, измеряемые некоторой установленной единицей длины и равные расстояниям от точки 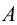
- по оси
— абсцисса, равная длине отрезка
;
- по оси
— ордината, равная длине отрезка
;
- по оси
— аппликата, равная длине отрезка
.
Три координаты точки однозначно определяют ее положение в пространстве.
Взаимно перпендикулярные плоскости, изображенные на рис.3, дают нам пространственный чертеж. Для получения трех проекций точки в плоскости чертежа плоскости проекций 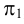
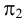
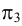
Фронтальная плоскость проекций 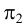
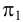
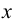
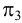
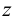
При совмещении плоскости 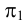
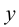
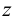
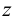
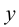
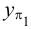
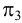
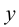
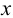
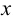
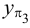
В результате образуется ортогональный чертеж, или эпюр (от франц. epure — чертеж, проект). На эпюре изображают только проекции геометрических объектов, а не сами объекты.
Любые две проекции точки, изображенные на эпюре, связаны между собой линией проекционной связи, перпендикулярной оси проекций (на чертеже ее обозначают штриховой линией):
горизонтальная и фронтальная проекции (точки
и
) расположены на линии проекционной связи, перпендикулярной оси
;
фронтальная и профильная проекции (точки
и
) — на линии проекционной связи, перпендикулярной оси
;
горизонтальная и профильная проекции (точки
и
) — на линии проекционной связи, перпендикулярной оси
.
Вследствие того, что отрезки 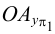
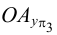
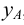
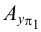
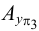
Каждая проекция точки 
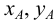
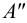
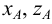
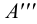
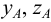
Положение точки 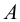
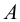
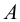
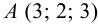
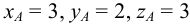
От аналитической формы задания точки легко перейти к графическому изображению этой точки на ортогональном чертеже.
Пример 1. Построить проекции точки 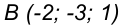
1. Выбираем единичный отрезок (рис.4).
2. С учетом знака откладываем на осях проекций координатные отрезки:
3. Отмечаем точки 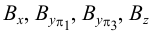
4. Из построенных точек 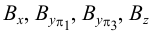
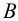
Две проекции точки, построенные на эпюре, однозначно определяют ее положение в пространстве. По двум проекциям заданной точки можно построить третью, и притом только одну.
Пример 2. Построить третью проекцию точки 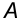
1. Даны фронтальная и профильная проекции точки 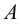
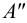
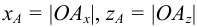
профильная проекция 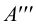
2. Из имеющихся проекций проводим линии проекционной связи, перпендикулярные осям проекций, и определяем координатные отрезки 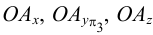
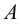
3. На пересечении линий проекционной связи с осями проекций отмечаем точки 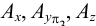
4. Строим третью, горизонтальную проекцию точки 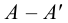
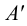
При определении точки 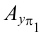
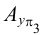
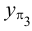
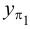
В зависимости от расположения точки относительно плоскостей проекций различают:
1) точки общего положения, не принадлежащие плоскостям проекций (к ним относится, например, точка А на рис.3);
2) точки частного положения, лежащие в плоскостях проекций 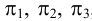
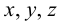
У точки общего положения все три координаты отличны от нуля.
Если точка лежит в плоскости проекций, то ее координата по оси, перпендикулярной этой плоскости проекций, равна нулю. Если точка лежит на оси проекций, то две другие ее координаты равны нулю. Если все три координаты точки равны нулю, то точка лежит в начале координат.
Рассмотрим некоторые частные случаи положения точки: когда точка лежит в какой-нибудь плоскости проекций или на какой-нибудь оси проекций.
Точка 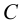
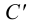
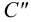
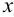
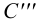
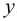
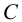
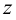
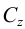
Точка 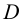
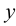
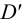
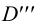
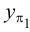
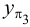
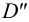
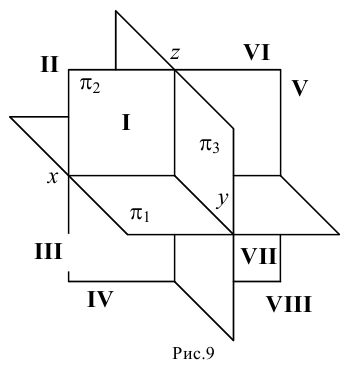
Октанты
Плоскости проекций 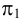
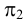
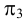
Нумерация октантов в полупространствах приведена на рис.9. Знаки координат в каждом из октантов указаны в табл.2.
Таблица 2
Знаки прямоугольных координат в различных октантах
Проекции отрезка прямой линии. Точка на прямой
Прямую линию можно рассматривать как совокупность точек. Из школьного курса геометрии известно, что через две точки можно провести прямую и притом только одну.
Пусть нам даны на эпюре точки 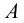
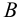
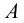
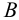
Таким образом, прямая линия на эпюре может быть задана двумя проекциями отрезка, принадлежащего этой прямой. По двум проекциям отрезка всегда можно построить его третью проекцию и притом только одну.
Если прямая не параллельна ни одной из плоскостей проекций, то она пересекает все плоскости проекций и не проецируется ни на одну из них в натуральную величину. Такую прямую называют прямой общего положения. Ни одна из ее проекций не параллельна осям. Прямая 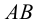
Точка принадлежит прямой линии, если ее проекции лежат на одноименных проекциях этой линии.
Если на прямой 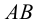
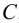
Таким образом, если точка принадлежит заданной прямой, то для построения проекций этой точки на эпюре необходимо и достаточно знать положение хотя бы одной проекции точки, поскольку недостающие проекции легко найти в пересечении линий проекционной связи с соответствующими проекциями прямой.
Прямые частного положения
Прямая, параллельная одной или двум плоскостям проекций, называется прямой частного положения.
Рассмотрим пример, когда прямая параллельна одной плоскости проекций. В этом случае прямая проецируется на эту плоскость в натуральную величину, а две другие проекции -параллельны осям проекций.
Горизонтальная прямая — прямая, параллельная плоскости 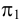
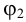
Фронтальная прямая — прямая, параллельная плоскости 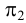
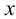
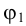
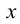
Профильная прямая — прямая, параллельная плоскости 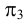
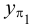
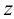
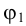
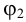
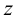
Если прямая параллельна двум плоскостям проекций, т.е. перпендикулярна третьей плоскости проекций, то на эти две плоскости проекции прямая проецируется в натуральную величину, а третья проекция представляет собой точку. Такие прямые называют проецирующими.
Горизонтально-проецирующая прямая — прямая, перпендикулярная плоскости 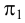
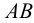
Фронтально-проецирующая прямая -прямая, перпендикулярная плоскости 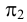
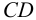
Профильно-проецирующая прямая — прямая, перпендикулярная плоскости 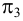
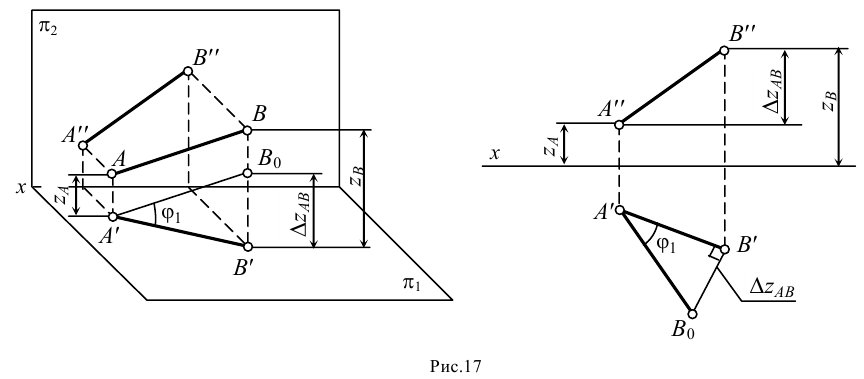
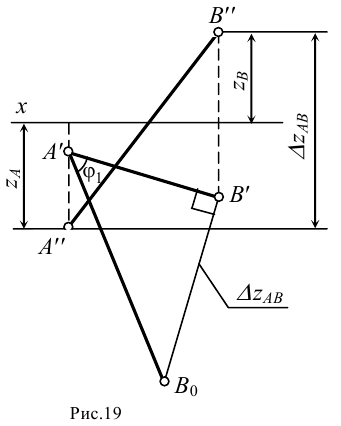
Определение натуральной величины отрезка прямой общего положения методом прямоугольного треугольника
Ортогональная проекция отрезка прямой общего положения на любую плоскость проекций всегда меньше длины самого отрезка. Рассмотрим правила определения натуральной величины отрезка прямой методом прямоугольного треугольника.
Предположим, что точки 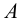
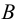
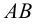
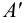
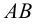

Рассмотрим стороны прямоугольного треугольника 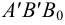
- • гипотенуза треугольника
определяет натуральную величину отрезка
;
- • один катет
представляет собой горизонтальную проекцию отрезка
;
- • второй катет
равен разности координат точек
и
по оси
:
.
На ортогональном чертеже оказывается достаточно данных для построения треугольника, равного рассмотренному (рис.17). Для этого к горизонтальной проекции 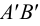
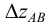
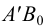
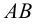
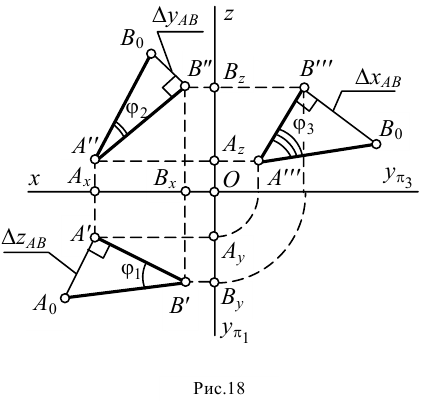
Истинную величину отрезка можно определить, построив прямоугольный треугольник, катетом которого является и фронтальная проекция отрезка (рис.18): при этом второй катет окажется равным разности координат 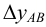
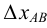
На рис.18 истинная величина отрезка 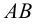
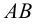
В общем случае, натуральная величина отрезка прямой общего положения равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция отрезка прямой, а вторым — разность «третьих» координат (табл.3).
Под термином «третья координата» подразумевается координата, которая отсутствует в проекции, выбранной в качестве катета прямоугольного треугольника. Так, горизонтальная проекция отрезка строится по координатам 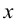
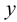
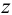
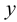
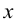
Таблица 3
Геометрические элементы при определении истинной величины отрезка примой 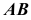
Координаты концов отрезка могут иметь разные знаки. Тогда разность координат определяется с учетом знака. Например, если координата 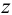
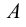
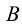
Угол наклона прямой к плоскости проекций — это угол между прямой и ее проекцией. Следовательно, определяя истинную величину отрезка прямой методом прямоугольного треугольника, одновременно можно найти и угол ее наклона к плоскости проекций. Угол между гипотенузой и соответствующей проекцией отрезка равен углу наклона этой прямой к данной плоскости проекций.
Пример 3. Определить истинную величину отрезка 
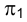
1. По табл.3 определяем, что для нахождения угла наклона к плоскости 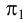
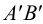
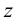
2. Определяем координаты по оси 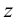
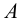
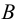
3. Строим прямоугольный треугольник, в котором за катет принимаем горизонтальную проекцию 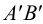
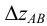
4. Гипотенуза построенного треугольника есть истинная величина отрезка 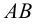
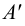
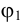
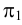
Следы прямой
Следом прямой называется точка пересечения прямой линии с плоскостью проекций. Прямая общего положения пересекает все три плоскости проекций и, следовательно, имеет три следа. Прямая линия частного положения не имеет следа на плоскости проекций, если она параллельна этой плоскости.
Выберем две точки, точку 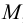
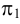
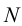
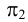
Точка пересечения 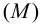
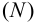
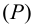
Следы прямой совпадают с проекциями этих следов в той плоскости, где они расположены: 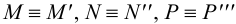
Поскольку точка 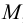
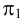
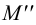
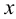
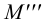
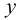
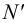
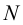
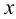
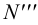
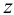
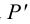
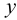
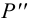
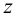
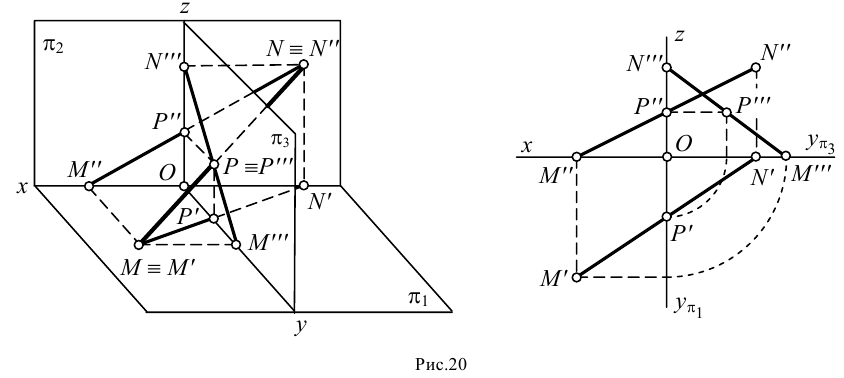
Охарактеризуем особенности построения каждой проекции каждого из трех следов на ортогональном чертеже (рис.20).
Горизонтальный след 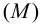
- фронтальная проекция горизонтального следа
лежит на пересечении фронтальной проекции прямой с осью
(с этой точки обычно начинают построения);
- горизонтальная проекция горизонтального следа
лежит на пересечении горизонтальной проекции прямой с линией проекционной связи, проведенной из проекции
перпендикулярно оси
;
- профильная проекция горизонтального следа
лежит на пересечении профильной проекции прямой с осью
.
Фронтальный след 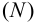
- горизонтальная проекция фронтального следа
лежит в точке пересечения горизонтальной проекции прямой с осью
;
- фронтальная проекция фронтального следа
лежит на пересечении фронтальной проекции прямой с линией проекционной связи, проведенной из точки
перпендикулярно оси
;
- профильная проекция фронтального следа
лежит на пересечении профильного следа прямой с осью
.
Профильный след 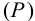
- горизонтальная проекция профильного следа
лежит на пересечении горизонтальной проекции прямой с осью
;
- фронтальная проекция профильного следа
лежит на пересечении фронтальной проекции прямой с осью
;
- профильная проекция профильного следа
находится в точке пересечения профильной проекции прямой с линией проекционной связи, проведенной из
перпендикулярно оси
.
Необходимо отметить, что построение профильных проекций следов 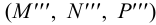
Пример 4. Построить проекции следов прямой 
1. Находим фронтальную проекцию горизонтального следа 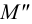
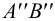
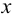
2. Из точки 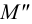
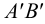
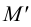
3. По двум проекциям 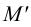
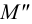
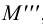
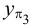
4. Находим горизонтальную проекцию фронтального следа 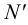
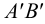
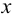
5. Из точки 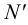
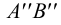
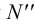
6. По двум проекциям фронтального следа 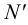
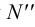
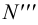
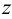
7. В пересечении 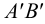
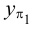
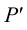
8. В пересечении 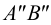
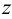
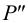
9. По двум проекциям 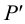
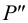
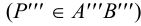
Взаимное положение двух прямых
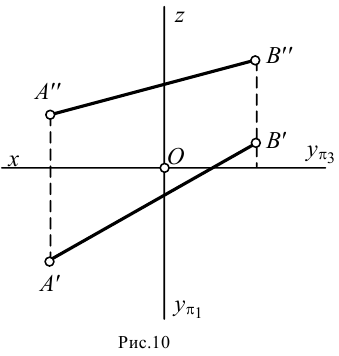
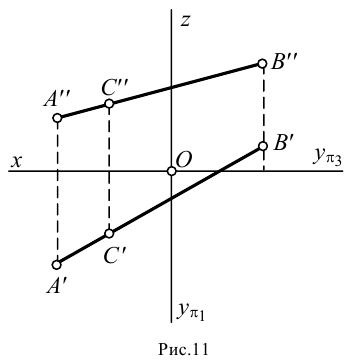
Две прямые могут пересекаться, быть параллельными друг другу и скрещиваться.
Пересекающиеся прямые имеют одну общую точку. Если прямые линии пересекаются, то одноименные проекции этих прямых тоже пересекаются (рис.22, а), причем проекции точки пересечения лежат на одной линии проекционной связи.
Параллельные прямые лежат в одной плоскости и не имеют общих точек. Одноименные проекции двух параллельных прямых параллельны между собой (рис.22, б).
Скрещивающиеся прямые, в отличие от пересекающихся и параллельных прямых, не лежат в одной плоскости. Хотя одноименные проекции двух скрещивающихся прямых и могут пересекаться, но точки их пересечения не лежат на одной линии проекционной связи (рис.22, в).
Две точки, лежащие на скрещивающихся прямых и на одном перпендикуляре к плоскости проекций, называются конкурирующими. Проекции конкурирующих точек лежат в точке пересечения одноименных проекций скрещивающихся прямых (точки / и 2 на фронтальной плоскости проекций, точки 3 и 4 на горизонтальной плоскости проекций — см. рис.22, в)
Проецирование плоских углов
Плоский угол проецируется на плоскость проекций без искажения, если плоскость угла параллельна плоскости проекций. Это справедливо в отношении любого угла — острого или тупого. Исключение составляет только прямой угол, который проецируется на плоскость проекций без искажения, если хотя бы одна его сторона параллельна плоскости проекций (рис.23).
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Проецирование плоскости
- Плоскость на эпюре Монжа
- Позиционные задачи
- Методы преобразования эпюра Монжа
- Взаимное положение плоскостей, прямой линии и плоскости
- Взаимное расположение точки, прямых и плоскостей
- Перпендикулярность геометрических объектов
- Метод замены плоскостей проекций
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🔍 Видео
7 класс, 28 урок, Аксиома параллельных прямыхСкачать

тема 8 3 Параллельное проектирование и его свойстваСкачать

Параллельная проекцияСкачать

Геометрия 7 класс (Урок№20 - Аксиома параллельных прямых.)Скачать

10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Параллельные прямые (задачи).Скачать

Параллельное проектирование и его свойства Изображение пространственных фигурСкачать

10 класс, 5 урок, Параллельность трех прямыхСкачать

Определение расстояние между параллельными прямыми (Способ замены плоскостей проекции).Скачать

Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Параллельные прямые. 6 класс.Скачать

Взаимное расположение прямых в пространстве. 10 класс.Скачать


















 — горизонтальную плоскость проекций;
— горизонтальную плоскость проекций; — фронтальную плоскость проекций;
— фронтальную плоскость проекций;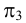 — профильную плоскость проекций.
— профильную плоскость проекций.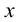 — абсцисса, равная длине отрезка
— абсцисса, равная длине отрезка 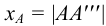 ;
;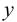 — ордината, равная длине отрезка
— ордината, равная длине отрезка 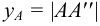 ;
;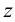 — аппликата, равная длине отрезка
— аппликата, равная длине отрезка 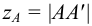 .
.
 горизонтальная и фронтальная проекции (точки
горизонтальная и фронтальная проекции (точки 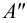 ) расположены на линии проекционной связи, перпендикулярной оси
) расположены на линии проекционной связи, перпендикулярной оси 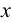 ;
; фронтальная и профильная проекции (точки
фронтальная и профильная проекции (точки 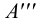 ) — на линии проекционной связи, перпендикулярной оси
) — на линии проекционной связи, перпендикулярной оси 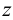 ;
; горизонтальная и профильная проекции (точки
горизонтальная и профильная проекции (точки 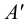 и
и  .
.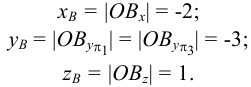
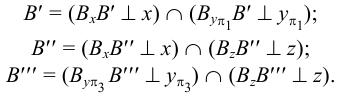
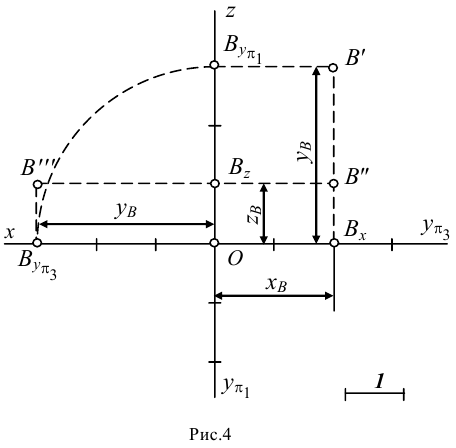
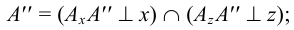
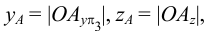
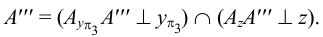
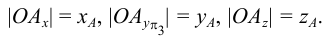
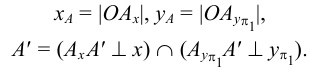
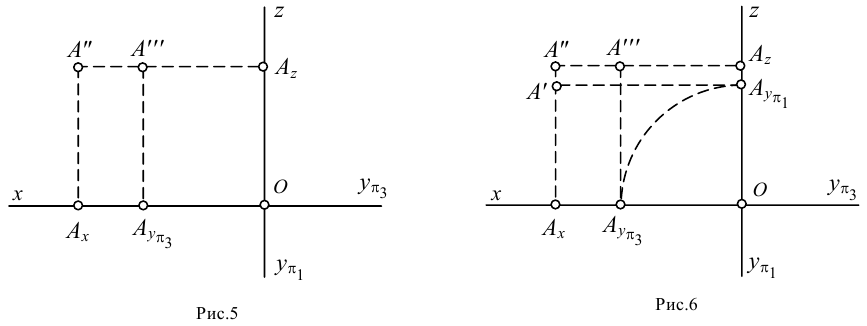
 определяет натуральную величину отрезка
определяет натуральную величину отрезка  представляет собой горизонтальную проекцию отрезка
представляет собой горизонтальную проекцию отрезка 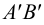 равен разности координат точек
равен разности координат точек  :
:  .
.

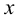 (с этой точки обычно начинают построения);
(с этой точки обычно начинают построения);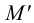 лежит на пересечении горизонтальной проекции прямой с линией проекционной связи, проведенной из проекции
лежит на пересечении горизонтальной проекции прямой с линией проекционной связи, проведенной из проекции 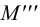 лежит на пересечении профильной проекции прямой с осью
лежит на пересечении профильной проекции прямой с осью 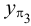 .
.
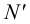 лежит в точке пересечения горизонтальной проекции прямой с осью
лежит в точке пересечения горизонтальной проекции прямой с осью  ;
; лежит на пересечении фронтальной проекции прямой с линией проекционной связи, проведенной из точки
лежит на пересечении фронтальной проекции прямой с линией проекционной связи, проведенной из точки 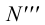 лежит на пересечении профильного следа прямой с осью
лежит на пересечении профильного следа прямой с осью 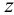 .
.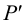 лежит на пересечении горизонтальной проекции прямой с осью
лежит на пересечении горизонтальной проекции прямой с осью 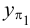 ;
;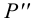 лежит на пересечении фронтальной проекции прямой с осью
лежит на пересечении фронтальной проекции прямой с осью 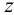 ;
;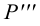 находится в точке пересечения профильной проекции прямой с линией проекционной связи, проведенной из
находится в точке пересечения профильной проекции прямой с линией проекционной связи, проведенной из 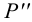 перпендикулярно оси
перпендикулярно оси 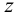 .
.