В исследовательской работе по теме «Решение задач с помощью кругов Эйлера», рассмотрено применение кругов Эйлера (или диаграмм Эйлера — Венна) при решении задач, которые обычным путём разрешимы лишь при составлении системы уравнений с тремя и более неизвестными. Леонард Эйлер — автор метода, говорил: «круги подходят для того, чтобы облегчить наши размышления». Действительно, Круги Эйлера помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.
- Скачать:
- Предварительный просмотр:
- Проект по математике на тему «Решение задач с помощью кругов Эйлера» (8 класс)
- Решение задач с помощью кругов
- Вступление Логические задачи составляют обширный класс нестандартных задач
- Актуальность Задачи имеют практический характер ,
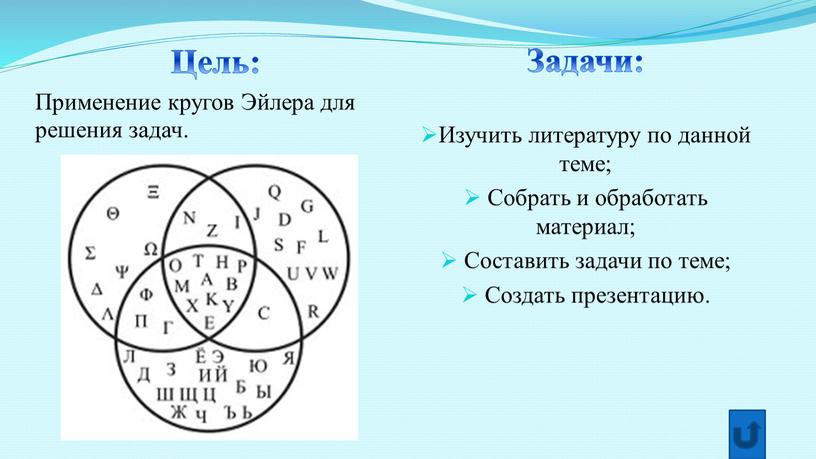
- Цель: Применение кругов Эйлера для решения задач
- Содержание
- Из биографии Леонарда Эйлера .
- Из биографии Леонарда Эйлера http://to-name
- Круги Эйлера Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами
- Задачи Задача 1 Задача 2 Задача 3
- Задача №1 В летнем лагере было 70 ребят
- Задача №2 Часть жителей одного города умеют говорить только по-русски, часть — только по-узбекски, и часть умеет говорить на обоих языках
- Задача №3 В классе несколько мальчиков собирали марки
- Задача №4 В школе зимой работали 3 спортивные секции — лыжная, хоккейная и конькобежная
- Задача №5 В магазине побывало 65 человек
- Задача №6 В классе 35 учеников
- Заключение В процессе изучения данной темы я расширила свои знания по математике, познакомилась с ещё одним способом решения задач, который был мне мало знаком, поэтому…
- Решение задач с помощью кругов Эйлера
- Пояснительная записка
- Основные понятия
- 2. Решение задач с помощью кругов Эйлера
- 2.1. «Обитаемый остров» и «Стиляги»
- 2.2. Задача про библиотеки
- 2.3. Гарри Поттер, Рон и Гермиона
- 2.4. Задача про любимые мультфильмы
- 2.5. Задача про Крейсер и Линкор
- 2.6. Задача про блондинок
- 2.7. Задача про кружки
- Задачи для самостоятельного решения
Видео:Окружность девяти точек, Эйлера, Фейербаха, Теркема...Скачать

Скачать:
| Вложение | Размер |
|---|---|
| Исследовательская работа по теме «Решение задач с помощью кругов Эйлера» | 482.43 КБ |
| Презентация к исследовательской работе «Решение задач с помощью кругов Эйлера» | 744.5 КБ |
Видео:#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Предварительный просмотр:
Решение задач с помощью кругов Эйлера
Автор: Цубикова Валерия Игоревна
МБОУ СОШ № 45 г.Сургут
7 в класс
Руководитель: Гордеева Светлана Николаевна
МБОУ СОШ № 45 г.Сургут
учитель математики
1. Введение. Историческая справка. 4 стр.
2. Круги Эйлера: почему один раз увидеть лучше, чем сто раз услышать?
2.1. Теоретические основы о кругах Эйлера. 5стр.
2.2. Решение задач с помощью кругов Эйлера. 7 стр.
3. Зачем нужны круги Эйлера? 13 стр.
4. Заключение. 14 стр.
5. Литература. 15 стр.
6. Приложение. 16 стр.
Цель моей исследовательской работы:
1) Выявление задач, которые можно решать с помощью кругов Эйлера;
2) Научиться решать задачи, используя круги Эйлера;
1) Изучить теоретические сведения по теме «Круги Эйлера»;
2) Посмотреть применение «кругов Эйлера» в реальной жизни.
Задачи на множества различных элементов (чисел и других объектов)
Множества и действия с ними.
2) Анализ решения готовых задач;
3) Решение задач, применяя арифметический метод и круги Эйлера;
4) Составление задач;
Применение кругов Эйлера позволяет решать задачи, которые обычным путём разрешимы лишь при составлении системы нескольких уравнений с несколькими неизвестными.
1. Введение. Историческая справка.
Леонард Эйлер ( 1707 — 1783 ) (Иллюстрация 1)
Эйлеру повезло: он родился в маленькой тихой Швейцарии, куда изо всей Европы приезжали мастера и ученые, не желавшие тратить дорогое рабочее время на гражданские смуты или религиозные распри. Так переселилась в Базель из Голландии семья Бернулли: уникальное созвездие научных талантов во главе с братьями Якобом и Иоганном. По воле случая юный Эйлер попал в эту компанию и вскоре сделался достойным членом базельского питомника гениев.
Эйлер принадлежит к числу гениев, чьё творчество стало достоянием всего человечества. До сих пор школьники всех стран изучают тригонометрию и логарифмы в том виде, какой придал им Эйлер. Студенты проходят высшую математику под руководством, первыми образцами которых явились классические монографии Эйлера. Он был прежде всего математиком, но он знал, что почвой, на которой расцветает математика, является практическая деятельность. Он оставил важнейшие труды по самым различным отраслям математики, механики, физики, астрономии и по ряду прикладных наук. Трудно даже перечислить все отрасли, в которых трудился великий учёный.
Его называли идеальным математиком 18 века.
Леонард Эйлер написал более 850 научных работ. В одной из них и появились круги. А впервые он их использовал в письмах к немецкой принцессе. Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления». Позднее аналогичный прием использовал ученый Джон Венн (Иллюстрация 2) — британский логик и философ; основные труды в области логики классов; и этот приём назвали «диаграммы Венна», который используется во многих областях: теория множеств, теория вероятностей, логика, статистика, компьютерные науки.
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов и они получили название «круги Эйлера-Венна».
Этот метод даёт более наглядное представление о возможном способе изображения условий, зависимости, отношений в логических задачах.
Во многих учебниках математики множество всех действительных чисел Эйлер изображено с помощью кругов, изображённых на рисунке (Иллюстрация 3) : N — Множество натуральных чисел, Z – множество целых чисел, Q – множество рациональных чисел, R – множество всех действительных чисел.
2. Круги Эйлера: почему один раз увидеть лучше, чем сто раз услышать?
2.1.Теоретические основы о кругах Эйлера.
Эйлеровы круги (круги Эйлера) — это принятый в логике способ моделирования, наглядного изображения отношений между объемами понятий с помощью кругов, предложенный знаменитым математиком Л. Эйлером (1707–1783).
Обозначение отношений между объемами понятий посредством кругов было применено еще представителем афинской неоплатоновской школы — Филопоном (VI в.), написавшим комментарии на «Первую Аналитику» Аристотеля.
Условно принято, что круг наглядно изображает объем одного какого-нибудь понятия. Объем же понятия отображает совокупность предметов того или иного класса предметов. Поэтому каждый предмет класса предметов можно изобразить посредством точки, помещенной внутри круга, как это показано на рисунке (Иллюстрация 4 а).
Группа предметов, составляющая вид данного класса предметов, изображается в виде меньшего круга, нарисованного внутри большего круга, как это сделано на рисунке (Иллюстрация 4б).
Такое именно отношение существует между объемами понятий «небесное тело» (А) и «комета» (B). Объему понятия «небесное тело» соответствует больший круг, а объему понятия «комета» — меньший круг. Это означает, что все кометы являются небесными телами. Весь объем понятия «комета» входит в объем понятия «небесное тело».
В тех случаях, когда объемы двух понятий совпадают только частично, отношение между объемами таких понятий изображается посредством двух перекрещивающихся кругов, как это показано на рисунке (иллюстрация 4в):
Такое именно отношение существует между объемом понятий «студент» и «спортсмен». Некоторые (но не все) студенты являются спортсменами; некоторые (но не все) спортсмены являются студентами. Незаштрихованная часть круга А отображает ту часть объема понятия «студент», которая не совпадает с объемом понятия «спортсмен»; незаштрихованная часть круга B отображает ту часть объема понятия «спортсмен», которая не совпадает с объемом понятия «студент». 3аштрихованиая часть, являющаяся общей для обоих кругов, обозначает студентов, являющихся спортсменами, и спортсменов, являющихся студентами.
Другой пример пересекающихся множеств. Пусть множество А – это ребята из нашего класса, которые зарегистрированы в социальной сети ВКонтакте.ru и множество В ребят, которые пользуются другой сетью – Facebook. Есть ребята, которые пользуются одновременно двумя сетями – это множество А и В . Данное множество образуется пересечением (общей частью) двух или более множеств.
Когда же ни один предмет, отображенный в объеме понятия A, не может одновременно отображаться в объеме понятия B, то в таком случае отношение между объемами понятий изображается посредством двух кругов, нарисованных один вне другого. Ни одна точка, лежащая на поверхности одного круга, не может оказаться на поверхности другого круга (Иллюстрация 4г).
Такое именно отношение существует, например, между понятиями «тупоугольный треугольник» и «остроугольный треугольник». В объеме понятия «тупоугольный треугольник» не отображается ни один остроугольный треугольник, а в объеме понятия «остроугольный треугольник» не отображается ни один тупоугольный треугольник.
Отношения между равнозначащими понятиями, объемы которых совпадают, отображаются наглядно посредством одного круга, на поверхности которого написаны две буквы, обозначающие два понятия, имеющие один и тот же объем (Иллюстрация 4д).
Такое отношение существует, например, между понятиями «автор и композитор песни «Пять причин» и исполнитель песни «Пять причин». Объемы этих понятий одинаковы, в них отобразилось одно и то же известное лицо — российский композитор и певец Игорь Николаев.
Нередко бывает и так: одному понятию (родовому) подчиняется сразу несколько видовых понятий, которые в таком случае называются соподчиненными. Отношение между такими понятиями изображается наглядно посредством одного большого круга и нескольких кругов меньшего размера, которые нарисованы на поверхности большего круга (Иллюстрация 4ж).
Такое именно отношение существует между понятиями «скрипка», «флейта», «пианино», «рояль», «барабан». Эти понятия в равной мере подчинены одному общему родовому понятию «музыкальные инструменты».
Круги, изображающие соподчиненные понятия, не должны касаться друг друга и перекрещиваться, так как объемы соподчиненных понятий несовместимы; в содержании соподчиненных понятий имеются, наряду с общими, различающие признаки. Эта схема отображает общее, что характерно для отношения любых соподчиненных понятий, взятых из различных областей знания. Это применимо к понятиям: «дом», «сарай», «ангар», «театр», подчиненных понятию «постройка»; к понятиям: «муха», «комар», «бабочка», «жук», «пчела», подчиненных понятию «насекомое» и т. д.
2.2. Решение задач с помощью кругов Эйлера
Рассмотрим несколько задач, которые могут быть решены с применением кругов Эйлера на уроках математики.
Из 52 школьников 23 собирают значки, 35 собирают марки, а 16 — и значки, и марки.
Остальные не увлекаются коллекционированием. Сколько школьников не увлекаются коллекционированием.
В условии этой задачи не так легко разобраться. Если сложить 23 и 35, то получится больше 52. Это объясняется тем, что некоторых школьников мы здесь учли дважды, а именно тех, которые собирают и значки, и марки.
чтобы легче решать задачу, представим ее данные на следующей схеме (Иллюстрация 5):
На этой схеме большой круг означает всех школьников, о которых идёт речь. Круг З изображает школьников, собирающих значки (всего их 23), а круг М — школьников, собирающих марки (всего их 35). В пересечении кругов З и М стоит число 16 — это те, кто собирает и значки, и марки. Значит, только значки собирает 23 — 16 = 7 человек, только марки собирает 35 — 16 = 19 человек. Всего марки и значкисобирает19 + 7 + 16 = 42 человека. Остаётся 52 — 42 = 10 человек, не увлечённых коллекционированием. Это число можно вписать в свободное поле круга.
Ответ: 10 человек.
В классе 15 мальчиков. Из них 10 человек занимается волейболом и 9 баскетболом. Сколько мальчиков занимается и тем, и другим?
Изобразим условие с помощью кругов Эйлера (Иллюстрация 6а). Этот рисунок подсказывает нам рассуждения. Разберём это рассуждение и впишем нужное число в каждую из образовавшихся на диаграмме частей (Иллюстрация 6б).
Только баскетболом занимается 15 — 10 = 5 мальчиков; только волейболом занимается 15 — 9 = 6 мальчиков; в двух секциях занимается 15 — (5+6) = 4 человека.
Ответ: 4 человека.
В доме 120 жильцов, у некоторых из них есть собаки и кошки. На рисунке круг С изображает жильцов с собаками, круг К — жильцов с кошками. Сколько жильцов имеют собак? Сколько жильцов имеют кошек? Сколько жильцов не имеют ни кошек, ни собак?
Собак имеют 15 + 8 = 23 человека; кошек 23 + 8 = 31 человек ; не имеют ни кошек, ни собак 120 — (15 + 8 +23) = 94 человека.
Ответ: 94 человека.
В группе из 80 туристов, приехавших на экскурсию а Москву, 52 хотят посетить Большой театр, 30 — Художественный театр, 12 хотят посетить оба театра, остальные в театры ходить не хотят. Сколько человек не собирается идти а театр?
Только большой театр посетят: 52-12=40 туристов;
только художественный театр посетят
80-(40+18+12)=10 туристов не собираются идти в театр (Иллюстрация 8).
Ответ: 10 человек.
При опросе 100 учеников 6-х классов выяснилось, что у 78 человек есть планшет, у 85 — смартфон, а у 8 учеников нет ни планшета, ни смартфона. У скольких учеников есть и планшет, и смартфон?
Имеют планшеты и смартфоны
100 — 8 = 92ученика;
имеют только смартфон 92 — 78 = 14 учеников 6-х классов;
имеют только планшет 92 — 85 = 7 учеников;
имеют и планшет, и смартфон 92 — (14+7)=71 ученик (Иллюстрация 9).
Ответ: 71 ученик.
На пикник поехали 92 человека. Бутерброды с колбасой взяли 50 человек, с сыром — 60 человек, с ветчиной — 40 человек, с сыром и колбасой — 30 человек, с колбасой и ветчиной = 15 человек, с сыром и ветчиной — 25 человек, 5 человек взяли с собой все три вида бутербродов, а несколько человек вместо бутербродов взяли пирожки. Сколько человек взяли с собой пирожки?
Решение. (Иллюстрация 10).
Изобразим условие с помощью кругов Эйлера.
Сначала отметим 5 человек, которые взяли с собой все три вида бутербродов;
15 — 5 = 10 человек взяли 2 вида бутербродов с колбасой и ветчиной;
25 — 5 = 20 человек взяли два вида бутербродов с сыром и ветчиной;
30 — 5 = 25 человек взяли два вида бутербродов с сыром и колбасой;
50 — (10 + 5 + 25) = 10 человек взяли бутерброды только с колбасой;
60 — (25 + 5 + 20) = 10 человек взяли бутерброды только с сыром;
40 — (10 + 5 + 20) = 5 человек взяли бутерброды только с ветчиной.
Пирожки взяли 92 — (10 + 25 + 10 + 10 + 5 + 20 + 5) = 7 человек.
Ответ: 7 человек.
Школа представила отчёт: «Всего в школе 60 шестиклассников, из них 37 отличников по математике, 33 — по русскому языку и 42 — по физкультуре. При этом у 21 человека «пятёрки» и по математике и по русскому, у 23 — по математике и по физкультуре, у 22 — по русскому и по физкультуре. При этом 20 человек учатся на «отлично» по всем трём предметам. Верен ли отчёт школы?
Решение. (Иллюстрация 11).
Изобразим условие с помощью кругов Эйлера.
Сначала отметим 20 человек, которые учатся на «отлично» по всем трём предметам.
Затем выясним, сколько человек имеет отличные оценки по двум предметам.
21 — 20 = 1 ученик имеет «пятёрки» по русскому и по математике;
22 — 20 = 2 ученика имеют » пятёрки» по русскому языку и физкультуре;
23 — 20 = 3 ученика имеют пятёрки по математике и физкультуре.
Далее выясним, сколько учеников имеют «пятёрки» только по одному из трёх предметов.
37 — (3 +20 +1) = 13 учеников имеют отличные оценки только по математике;
33 — (1 + 20 + 2) = 10 учеников учатся на «отлично» по русскому языку;
42 — (3 + 20 +2) = 17 учеников имеют «пятёрки» по физкультуре.
Выясним, совпадает ли количество учеников — отличников с количеством шестиклассников в школе.
13 + 1 + 10 +2 + 20 + 3 +17 = 66 учеников учатся на отлично.
Ответ: отчёт школы неверен.
В классе 30 человек. 20 из них каждый день пользуются метро, 15 – автобусом, 23 – троллейбусом, 10 – и метро, и троллейбусом, 12 – и метро, и автобусом, 9 – и троллейбусом, и автобусом. Сколько человек ежедневно пользуется всеми тремя видами транспорта?
Решение. (Иллюстрация 12).
1 способ. Для решения опять воспользуемся кругами Эйлера. Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются
только метро и троллейбусом – (10 – х) человек,
только автобусом и троллейбусом – (9 – х) человек,
только метро и автобусом – (12 – х) человек.
Найдем, сколько человек пользуется одним только метро:
20 – (12 – х) – (10 – х) – х = х – 2.
Аналогично получаем: х – 6 – только автобусом и х + 4 – только троллейбусом, так как всего 30 человек, составляем уравнение:
х + (12 – х) + (9 – х) + (10 – х) + (х + 4) + (х – 2) + (х – 6) = 30,
отсюда х = 3.
2 способ. А можно эту задачу решить задачу другим способом: 20 + 15 + 23 – 10 – 12 – 9 + х = 30, 27 + х = 30, х = 3 . Здесь сложили количество учеников, которые пользуются хотя бы одним видом транспорта и из полученной суммы вычли количество тех, кто пользуется двумя или тремя видами и, поэтому, вошли в сумму 2-3 раза. Таким образом, получили количество всех учеников в классе.
Ответ. 3 человека ежедневно пользуются всеми тремя видами транспорта.
Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах, созданных киностудией «Мельница». В частности, вопросы были о мультфильмах, повествующих о приключениях трёх самых известных богатырей — Алёши Поповича, Добрыни Никитича и Ильи Муромца.
Оказалось, что большинству из них нравятся «Три богатыря и Шамаханская царица», «Три богатыря на дальних берегах» и «Три богатыря. Ход конём». В анкетировании принимали участие 38 учеников. Мультфильм «Три богатыря на дальних берегах, нравится 21 ученику. Причем трем среди них нравятся еще и «Три богатыря. Ход конём», шестерым — «Три богатыря и Шамаханская царица. «, а один ребенок одинаково любит все три мультфильма. У мультфильма «Три богатыря. Ход конём» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким шестиклассникам нравится мультфильм «Три богатыря и Шамаханская царица».
Решение. (Иллюстрация 13 )
Так как по условиям задачи у нас даны три множества, чертим три круга. А так как по ответам ребят выходит, что множества пересекаются друг с другом, чертеж будет выглядеть так:(Иллюстрация 13а).
Мы помним, что по условиям задачи среди фанатов мультфильма «Три богатыря. Ход конём» пятеро ребят выбрали два мультфильма сразу: (Иллюстрация 13б)
Выходит, что (Иллюстрация 13в):
21 – 3 – 6 – 1 = 11 – ребят выбрали только «Три богатыря на дальних берегах»
13 – 3 – 1 – 2 = 7 – ребят в последнее время смотрят только «Три богатыря: Ход конём»
Осталось только разобраться, сколько шестиклассников двум другим вариантам предпочитает мультфильм «Три богатыря и Шамаханская царица».
От всего количества учеников отнимаем всех тех, кто любит два других мультфильма или выбрал несколько вариантов:
38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Три богатыря и Шамаханская царица» (Иллюстрация 13 г).
Теперь смело можем сложить все полученные цифры и выяснить, что:
мультфильм «Три богатыря и Шамаханская царица».
выбрали 8 + 2 + 1 + 6 = 17 человек. Это и есть ответ на поставленный в задаче вопрос.
Ответ: 17 человек.
3. Зачем нужны круги Эйлера?
Круги Эйлера имеют прикладное назначение, то есть с их помощью на практике решаются задачи на объединение или пересечение множеств в математике, логике, менеджменте и не только.
Если говорить о видах кругов Эйлера, то можно разделить их на те, что описывают объединение каких-то понятий (например, соотношение рода и вида) – мы их рассмотрели на примере в начале работы.
А также на те, что описывают пересечение множеств по какому-то признаку. Таким принципом руководствовался Джон Венн в своих схемах. И именно он лежит в основе многих популярных в интернете мемов. Вот вам один из примеров таких кругов Эйлера:(Иллюстрация 14.)
Забавно, правда? И главное, все сразу становится понятно. Можно потратить много слов, объясняя свою точку зрения, а можно просто нарисовать простую схему, которая сразу расставит все по местам.
Кстати, если вы не можете определиться, какую профессию выбрать, попробуйте нарисовать схему в виде кругов Эйлера. Возможно, чертеж вроде этого поможет вам определиться с выбором: (Иллюстрация 15)
Те варианты, которые окажутся на пересечении всех трех кругов, и есть профессия, которая не только сможет вас прокормить, но и будет вам нравиться.
Например (Иллюстрация 16):
В результате работы над данной темой я изучила теоретический материал по теме «Круги Эйлера» и пришла к следующим выводам:
1. Круги Эйлера – не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Причем не только абстрактных задач на школьных уроках, но и вполне себе житейских проблем. Выбора будущей профессии, например.
2. Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко решить задачи, которые обычным путем разрешимы лишь при составлении системы трех уравнений с тремя неизвестными. Таким образом, моя гипотеза подтвердилась. Автор метода — ученый Леонард Эйлер, говорил о названных его именем схемах: «круги подходят для того, чтобы облегчить наши размышления». Я согласна с его словами. Круги Эйлера помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.
- Депман,И.Я., Виленкин, Н.Я. За страницами учебника математики Пособие для учащихся 5 – 6 кл. [ Текст ] / И.Я Депман. М.: Просвещение, 1999.
2. Фарков, А.В. Математические олимпиады в школе.5–11 классы. [ Текст ] / А.В. Фарков. М.: Айрис–пресс, 2007.
3. Задачи для внеклассной работы по математике в V – VI классах: Пособие для учителей [ Текст ] / Сост. В.Ю. Сафонова. Под ред. Д.Б. Фукса, А. Л. Гавронского. М.: МИРОС, 1993.
4. Игнатьев. Е.И. В царстве смекалки, или Арифметика для всех: Книга для семьи и школы. Опыт математической хрестоматии в 3 книгах/Худож. Н.Я. Бойко. – Ростов н/Д: Кн. Изд-во, 1995.
5. Шарыгин И. Ф., Шевкин А. В. Математика: Задачи на смекалку: Учеб. пособие для 5 – 6 кл. общеобразоват. учреждений. – 5-е изд. – М.: Просвещение, 2000. – 95 с.: ил.
6. Математика: 6 класс: Дидакт. материалы для общеобразова. учеб. заведений/Г.В.Дорофеев, С.Б.Суворова, И.Ф.Шарыгин и др.- М.: Дрофа, 1996.
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Проект по математике на тему «Решение задач с помощью кругов Эйлера» (8 класс)
Видео:16 задание. Профильный ЕГЭ 2023. 9 точек окружности, окружность Эйлера. Что это?Скачать

Решение задач с помощью кругов
Решение задач с помощью кругов Эйлера
Работу выполнила ученица 8 класса МБОУ Сарасинской СОШ
Запольская Анастасия.
Руководитель:
Мордовских Надежда Васильевна, учитель математики
МБОУ Сарасинская СОШ Алтайского района
Видео:Прямая ЭйлераСкачать

Вступление Логические задачи составляют обширный класс нестандартных задач
Логические задачи составляют обширный класс нестандартных задач.
Существует множество приемов, которые используются при решении текстовых логических задач. Очень часто найти решение задачи помогает рисунок. Использование рисунка делает решение задачи простым и наглядным. Решение любой задачи можно красиво оформить. Задачи, решаемые с помощью кругов Эйлера, предлагаются на математических олимпиадах, но в школьной программе на изучение этой темы отводится мало часов.
Видео:Окружность. 7 класс.Скачать

Актуальность Задачи имеют практический характер ,
Задачи имеют практический характер ,
Заставляют задумываться,
Подходить к решению какой-либо проблемы с другой стороны,
Уметь выбирать из множества способов решения, наиболее простой, легкий путь.
Видео:Окружность Эйлера (окружность 9 точек) и прямая ЭйлераСкачать

Цель: Применение кругов Эйлера для решения задач
Цель:
Применение кругов Эйлера для решения задач.
Задачи:
Изучить литературу по данной теме;
Собрать и обработать материал;
Составить задачи по теме;
Создать презентацию.
Видео:Круги Эйлера в реальной жизни. Математика на QWERTYСкачать

Содержание
Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Из биографии Леонарда Эйлера .
Из биографии Леонарда Эйлера
Эйлер Леонард (1707—1783), математик, физик, механик, астроном.
Родился 15 апреля 1707 г. в Базеле (Швейцария). Окончил местную гимназию, слушал в Базельском университете лекции И. Бернулли. В 1723 г. получил степень магистра. В 1726 г. по приглашению Петербургской академии наук приехал в Россию и был назначен адъюнктом по математике.
Видео:#161. САМАЯ КРАСИВАЯ ФОРМУЛА В МАТЕМАТИКЕ — ФОРМУЛА ЭЙЛЕРА: e^(iπ)+1=0Скачать

Из биографии Леонарда Эйлера http://to-name
Из биографии Леонарда Эйлера
Видео:Теорема Эйлера | Доказательство.Скачать

Круги Эйлера Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами
Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами. Используется в математике, логике, менеджменте и других прикладных направлениях. А впервые Эйлер их использовал в письмах к немецкой принцессе. Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления». При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов, и они получили название «круги Эйлера».
Видео:ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

Задачи Задача 1 Задача 2 Задача 3
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Задача №1 В летнем лагере было 70 ребят
В летнем лагере было 70 ребят. 27 из них занимаются в драмкружке, 32 — поют в хоре, 22 — спортсмены. В драмкружке 10 ребят из хора, в хоре — 6 спортсменов, в драмкружке — 8 спортсменов. 3 спортсмена посещают и драмкружок, и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят увлекаются спортом?
27 — (10 + 5) = 12 (ребят) — занимаются в драмкружке,
в хоре: 32 — (110 + 3) = 19 (ребят);
занимаются спортом: 22 — (8 + 3) = 11 (ребят);
70 — (27 + 19 + 3 + 11) = 10 (ребят) — не занимаются ничем. Ответ : не увлечены ничем 10 ребят; увлечены спортом 11 ребят.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Задача №2 Часть жителей одного города умеют говорить только по-русски, часть — только по-узбекски, и часть умеет говорить на обоих языках
Часть жителей одного города умеют говорить только по-русски, часть — только по-узбекски, и часть умеет говорить на обоих языках. По-узбекски говорят 85% всех жителей, а по-русски — 75%. Сколько % жителей говорят на обоих языках?
75 % + 85 % = 160 %;
160 % — 100 % = 60 %,
или 100 % — 85 % = 15 % — говорят только по-русски;
75 % — 15 % = 60 % — говорят на обоих языках.
Ответ: 60%.
Видео:ЛШУ 2021. Окружность Эйлера. Наталья НетрусоваСкачать

Задача №3 В классе несколько мальчиков собирали марки
В классе несколько мальчиков собирали марки. 15 человек собирали марки России, 11 человек собирали иностранные марки, из них 6 человек собирали и марки России, и иностранные марки. Сколько мальчиков в классе собирали марки? Сколько мальчиков в классе собирали только марки России, и сколько мальчиков собирали только иностранные марки?
15 — 6 = 9 (мальчиков) — собирали только марки России,
11 — 6 = 5 (мальчиков) — собирали только иностранные марки;
(15 + 11) — 6 = 20 Мальчиков) — всего собирали марок.
Ответ: 20; 9; 5.
Видео:Круги Эйлера. Логическая задача на множества. Иностранные языкиСкачать

Задача №4 В школе зимой работали 3 спортивные секции — лыжная, хоккейная и конькобежная
В школе зимой работали 3 спортивные секции — лыжная, хоккейная и конькобежная. В них занимались 38 человек. Известно, что в лыжной секции занимался 21 человек, среди которых 3 человека занимались ещё в конькобежной секции, 6 человек — ещё в хоккейной секции и 1 человек занимался одновременно во всех трёх секциях. В конькобежной секции занимались 13 человек, среди которых 5 человек занимались одновременно в двух секциях. Сколько человек занимались в хоккейной секции?
Только коньками занимались: 13 — 2 — 2 — 1 = 8 (человек);
тогда только хоккеем занимались: 38 — 21 — 8 — 2 = 7 (человек);
всего хоккеем занимались: 7+ 5 + 1 + 2 = 15 (человек). Ответ: 15 человек.
Видео:#234. Формула Эйлера | Свойства отрезков хорд и секущихСкачать

Задача №5 В магазине побывало 65 человек
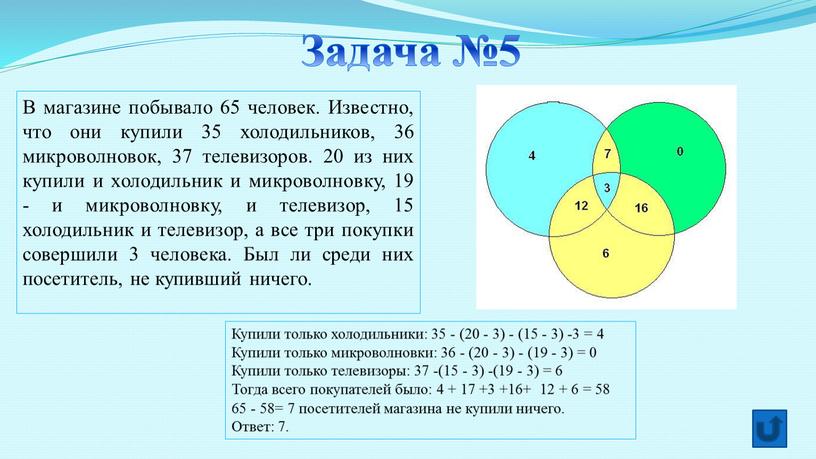
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 — и микроволновку, и телевизор, 15 холодильник и телевизор, а все три покупки совершили 3 человека. Был ли среди них посетитель, не купивший ничего.
Купили только холодильники: 35 — (20 — 3) — (15 — 3) -3 = 4 Купили только микроволновки: 36 — (20 — 3) — (19 — 3) = 0 Купили только телевизоры: 37 -(15 — 3) -(19 — 3) = 6 Тогда всего покупателей было: 4 + 17 +3 +16+ 12 + 6 = 58 65 — 58= 7 посетителей магазина не купили ничего.
Ответ: 7.
Видео:Котика ударило током, 10 т. ВольтСкачать

Задача №6 В классе 35 учеников
В классе 35 учеников. Из них: 20 школьников занимаются в математическом кружке, 11 – в экологическом, 10 ребят не посещают эти кружки. Сколько экологов увлекается математикой?
35 – 10 = 25 (учеников) – посещают кружки,
25 – 20 = 5 (учеников) – посещают экологический кружок,
11 – 5 = 6 (учеников) – посещают оба кружка.
Ответ: 6 экологов увлекаются математикой.
Видео:11 класс, 49 урок, Задача ЭйлераСкачать

Заключение В процессе изучения данной темы я расширила свои знания по математике, познакомилась с ещё одним способом решения задач, который был мне мало знаком, поэтому…
В процессе изучения данной темы я расширила свои знания по математике, познакомилась с ещё одним способом решения задач, который был мне мало знаком, поэтому я никогда не применяла его на практике.
Данный материал можно будет использовать на некоторых уроках, для проведения кружков, факультативных занятий по математике. Материал, используемый в работе, пригодится для решения задач занимательного характера, позволит применять методы и правила для решения нестандартных задач. Приобретенные сведения и знания способствуют повышению интеллектуального развития, помогают развить умение наблюдать, анализировать, рассуждать, что немаловажно в современной жизни.
Видео:Прямая ЭйлераСкачать

Решение задач с помощью кругов Эйлера
Классы: 5 , 6 , 7
Ключевые слова: круги Эйлера
Пояснительная записка
Очень часто решение задачи помогает найти рисунок. Использование рисунка делает решение простым и наглядным.
В данной разработке приведены примеры решения задач с помощью кругов Эйлера. Это не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Они помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.
С данным способом решения задач учащихся можно познакомить как на уроках, так и на кружковых занятиях.
Главной целью этой работы является помощь учителям математики для подготовки учащихся к олимпиадам, а также к экзаменам.
Основные понятия
Понятие множества − одно из первичных в математике. Поэтому очень трудно дать ему какое-либо определение, которое бы не заменяло слово «множество» каким-нибудь равнозначным выражением, например, совокупность, собрание элементов и т.д. Элементы множества − это то, из чего это множество состоит, например, каждый ученик вашего класса есть элемент множества школьников.
Пересечение множеств в теории множеств — это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам.
Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.
2. Решение задач с помощью кругов Эйлера
2.1. «Обитаемый остров» и «Стиляги»
Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек — фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?
Решение:
Чертим два множества таким образом:
6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.
1. 15 — 6 = 9 — человек, которые смотрели только «Обитаемый остров»,
2. 11- 6 = 5 — человек, которые смотрели только «Стиляги».
Ответ: 5 человек.
2.2. Задача про библиотеки
Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 — в районной.
- Являются читателями обеих библиотек;
- Не являются читателями районной библиотеки;
- Не являются читателями школьной библиотеки;
- Являются читателями только районной библиотеки;
- Являются читателями только школьной библиотеки?
Решение:
Чертим два множества таким образом:
1) 20+ 25 — 35 = 10 (человек) — являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.
2) 35 — 20 = 15 (человек) — не являются читателями районной библиотеки,
3) 35 — 25 = 10 (человек) — не являются читателями школьной библиотеки,
4) 35- 20 = 10 (человек) — являются читателями только районной библиотеки,
5) 35- 20 = 15 (человек) — являются читателями только школьной библиотеки.
Очевидно, что вопросы 2 и 5, а также 3 и 4 — равнозначны и ответы на них совпадают.
Ответ: 10 человек; 15 человек; 10 человек; 10 человек; 15 человек.
2.3. Гарри Поттер, Рон и Гермиона
На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?
Решение:
Учитывая условия задачи, сделаем чертеж:
Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги — Гермиона, то 11 — 4 — 2 = 5 — книг прочитал только Гарри.
Следовательно, 26 — 7 — 2 — 5 — 4 = 8 — книг прочитал только Рон.
Ответ: 8 книг.
2.4. Задача про любимые мультфильмы
Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».
Решение:
Чертим три круга, таким образом:
Из условия знаем, что трем ученикам нравиться и «Белоснежка и семь гномов», и «Волк и теленок», шестерым — «Белоснежка и семь гномов» и «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма.
Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу, т.е. 5 — 3 = 2 — ученика выбрали «Волк и теленок» и «Губка Боб Квадратные Штаны».
1) 21 — 3 — 1 — 6 = 11 — учеников выбрали только «Белоснежка и семь гномов»,
2) 13 — 3 — 1 — 2 = 7 — учеников выбрали — «Волк и теленок»,
3) 38 — (11 + 3 + 1 + 2 + 6 + 7) = 8 — ребят выбрали «Губка Боб Квадратные Штаны».
4) 8 + 2 + 1 + 6 = 17 — человек выбрали мультик «Губка Боб Квадратные Штаны».
Ответ: 17 учеников.
2.5. Задача про Крейсер и Линкор
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.
Найдено страниц, тыс.
Крейсер и Линкор
Какое количество страниц (в тысячах) будет найдено по запросу Крейсер и Линкор? (Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.)
Решение:
При помощи кругов Эйлера изобразим условия задачи.
1) 4800 + 4500 — 7000 = 2300 (тыс. страниц) — найдено по запросу Крейсер и Линкор,
2) 4800 — 2300 = 2500 (тыс. страниц) — найдено по запросу Крейсер,
3) 4500 — 2300 = 2200 (тыс. страниц) — найдено по запросу Линкор.
Ответ: 2300 тыс. страниц.
2.6. Задача про блондинок
Каждый ученик класса — либо девочка, либо блондин, либо любит математику. В классе 20 девочек, из них 12 блондинок, но одна блондинка любит математику. Всего в классе 24 ученика — блондина, математику из них любят 12, а всего учеников (мальчиков и девочек), которые любят математику, 17, из них 6 девочек. Сколько учеников в данном классе?
Решение:
Изобразим с помощью кругов Эйлера данные из задачи:
1) 12 — 1 = 11 (учеников) — девочек блондинок,
2) 12 — 1 = 11 (учеников) — блондины и любят математику,
3) 6 — 1 = 5 (учеников) — девочек, которые любят математику,
4) 20 — 11 — 1 — 5 = 3 (ученика) — девочки,
5) 24 — 11 — 1 — 11 = 1 (ученик) — блондин,
6) 17- 5 — 1 — 11 = 0 (учеников) — любят математику,
7) 3 + 1 + 0 + 5 + 11 + 11 + 1 = 32 (ученика) — всего в классе.
Ответ: 32 ученика.
2.7. Задача про кружки
В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?
Решение:
Учитывая условия задачи, сделаем чертеж:
1) 10 — 3 = 7 (ребят) — посещают драмкружок и хор,
2) 6 — 3 = 3 (ребят) — поют в хоре и занимаются спортом,
3) 8 — 3 = 5 (ребят) — занимаются спортом и посещают драмкружок,
4) 27 — 7 — 3 — 5 = 12 (ребят) — посещают драмкружок,
5) 32 — 7 3 — 3 = 19 (ребят) — поют в хоре,
6) 22 — 5 — 3 — 3 = 11 (ребят) — увлекаются спортом,
7) 70 — (12 + 19 + 11 + 5+ 7 + 3 + 3) = 10 (ребят) — не поют в хоре, не увлекаются спортом и не занимаются в драмкружке.
Ответ: 10 человек и 11 человек.
Задачи для самостоятельного решения
1. На фирме работают 67 человек. Из них 47 знают английский язык, 35 — немецкий язык, а 23 — оба языка. Сколько человек фирмы не знают ни английского, ни немецкого языков?
2. Из 40 учащихся нашего класса 32 любят молоко, 21 — лимонад, а 15 — и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?
3. 12 моих одноклассников любят читать детективы, 18 — фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?
4. Из тех 18 моих одноклассников, которые любят смотреть триллеры, только 12 не прочь посмотреть и мультфильмы. Сколько моих одноклассников смотрят одни «мультики», если всего в нашем классе 25 учеников, каждый из которых любит смотреть или триллеры, или мультфильмы, или и то и другое?
5. Из 29 мальчишек нашего двора только двое не занимаются спортом, а остальные посещают футбольную или теннисную секции, а то и обе. Футболом занимается 17 мальчишек, а теннисом — 19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?
6. В одном классе 25 учеников. Из них 7 любят груши, 11 — черешню. Двое любят груши и черешню; 6 — груши и яблоки; 5 — яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки?
7. В конкурсе красоты участвовали 22 девушки. Из них 10 было красивых, 12 — умных и 9 — добрых. Только 2 девушки были и красивыми, и умными; 6 девушек были умными и одновременно добрыми. Определите, сколько было красивых и в то же время добрых девушек, если я скажу вам, что среди участниц не оказалось ни одной умной, доброй и вместе с тем красивой девушки?
8. В нашем классе 35 учеников. За первую четверть пятерки по русскому языку имели 14 учеников; по математике — 12; по истории — 23. По русскому и математике — 4; по математике и истории — 9; по русскому языку и истории — 5. Сколько учеников имеют пятерки по всем трем предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по одному из этих предметов?
9. Из 100 человек 85 знают английский язык, 80 — испанский, 75 — немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три языка?
10. Из сотрудников фирмы 16 побывали во Франции, 10 — в Италии, 6 — в Англии; в Англии и Италии — 5; в Англии и Франции — 6; во всех трех странах — 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?
Список использованных источников
1. Баженов И.И, Порошкин А.Г., Тимофеев А.Ю., Яковлев В.Д. Задачи для школьных математических кружков: учеб. пособие / Сыктывкар: Сыктывкарский университет, 2006.
2. Марков И.С. Новые олимпиады по математике — Ростов н/Д: Феникс, 2005.