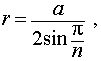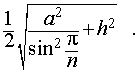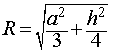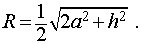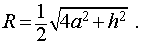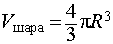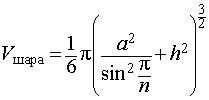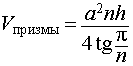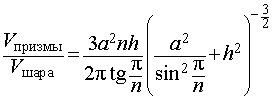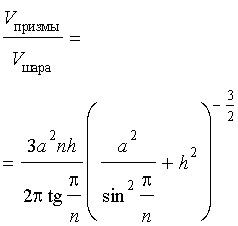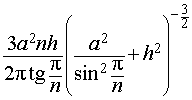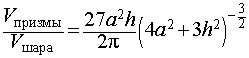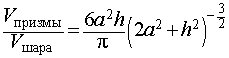Описанная окружность около треугольной призмы

Призма, вписанная в сферу. Свойства призмы, вписанной в сферу

Радиус сферы, описанной около правильной n — угольной призмы

Отношение объема правильной n — угольной призмы к объему шара, ограниченного описанной около этой призмы сферой

Видео:Решение А18 Прямая треугольная призма. Описанная около треугольника окружность.Скачать

Призма, вписанная в сферу. Свойства призмы, вписанной в сферу

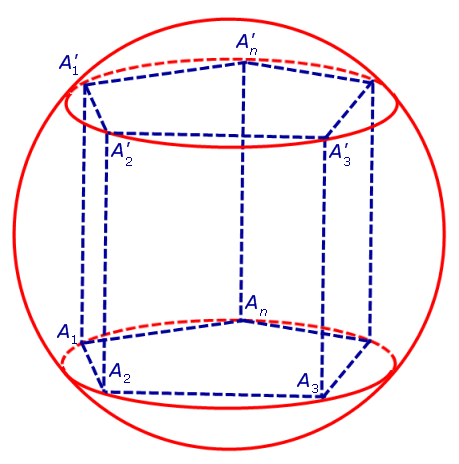
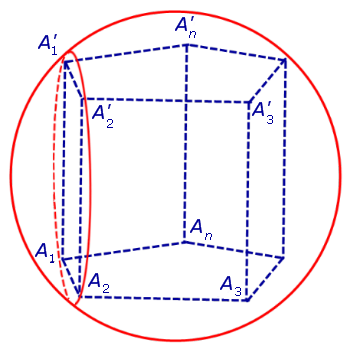
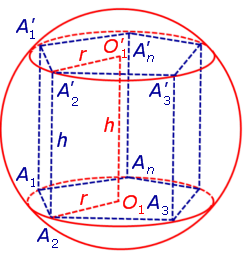
Определение 1. Призмой, вписанной в сферу, называют такую призму, все вершины которой лежат на сфере (рис. 1).

Определение 2. Если призма вписана в сферу, то сферу называют описанной около призмы.

Теорема. Около призмы можно описать сферу тогда и только тогда, когда выполнены следующие два условия:

1. Призма является прямой призмой;
2. Около оснований призмы можно описать окружности.

Доказательство. Докажем сначала, что если n – угольная призма A₁A₂ . A_nA’₁A’₂ . A’_n вписана в сферу, то оба условия теоремы выполнены.

Для этого заметим, что плоскость каждого из оснований призмы пересекает сферу по окружности, на которой лежат вершины этого основания. Таким образом, многоугольники, являющиеся основаниями призмы, оказываются вписанными в окружности (рис. 1), то есть второе условие теоремы выполнено.

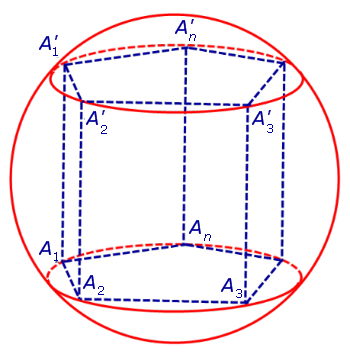
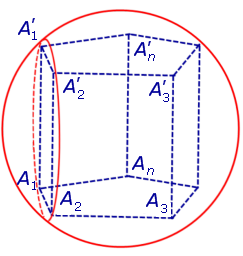
Каждая из боковых граней призмы также вписана в окружность (рис. 2).

Рассмотрим какое-нибудь боковое ребро призмы, например, A₂A’₂. Поскольку это ребро перпендикулярно к ребрам основания A₁A₂ и A₂A₃ , то в силу признака перпендикулярности прямой и плоскости заключаем, что боковое ребро A₂A’₂ перпендикулярно к плоскости основания призмы, то есть призма является прямой призмой.

Таким образом, мы доказали, что, если призма вписана в сферу, то оба условия теоремы выполнены.

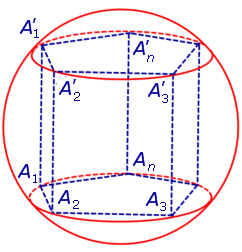
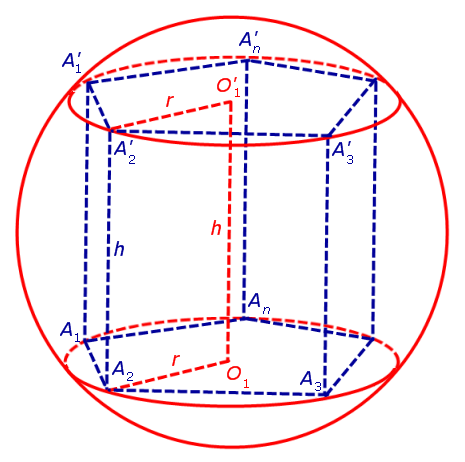
Для этого обозначим символом O₁ центр окружности радиуса r , описанной около нижнего основания призмы, а символом O’₁ обозначим центр окружности, описанной около верхнего основания призмы (рис. 3).

Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы описанных около них окружностей будут равны.

Согласно утверждению 1 из раздела «Призмы, вписанные в цилиндры» отрезок O₁O’₁, соединяющий центры окружностей, описанных около нижнего и верхнего оснований призмы, параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок O₁O’₁ перпендикулярен плоскости основания призмы и равен h.

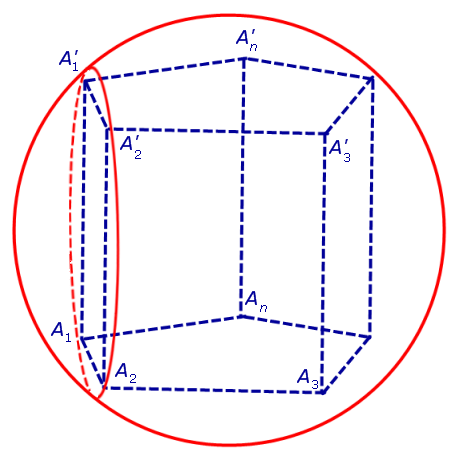
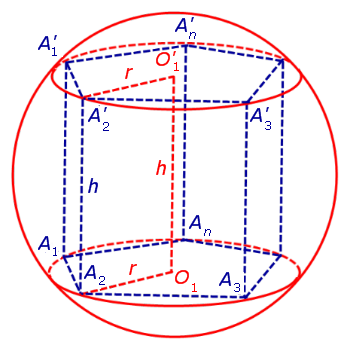
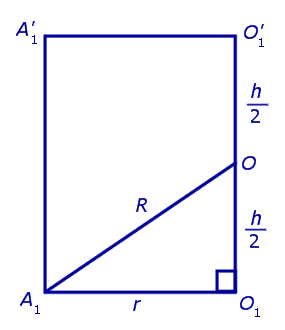
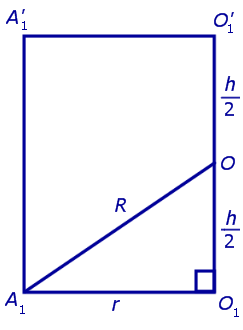
Обозначим буквой O середину отрезка O₁O’₁ и докажем, что все вершины призмы будут находиться на одном и том же расстояниии от точки O (рис. 4).

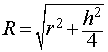(1)

от всех вершин призмы. Отсюда следует, что точка O является центром сферы радиуса R , описанной около призмы.

Следствие 1. Около любой прямой треугольной призмы можно вписать сферу.

Следствие 2. Около любого прямоугольного параллелепипеда (в частности, около куба прямоугольного параллелепипеда (в частности, около куба ) можно описать сферу.

Следствие 3. Около любой правильной призмы можно описать сферу.

Для доказательства следствия 3 достаточно заметить, что правильная n – угольная призма – это прямая призма, основания которой являются правильными n – угольниками, а около любого правильного n – угольника можно описать окружность.

Видео:Геометрия Объем правильной треугольной призмы равен 25√3. Радиус окружности, описанной околоСкачать

Радиус сферы, описанной около правильной n — угольной призмы

то из формулы (1) получаем выражение для радиуса описанной сферы

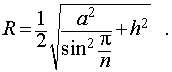(2)

Ответ.

Следствие 6. Радиус сферы, описанной около около правильной шестиугольной призмы с высотой h и ребром основания a равен

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Отношение объема правильной n — угольной призмы к объему шара, ограниченного описанной около призмы сферой

Задача 2. Около правильной n — угольной призмы с высотой h и ребром основания a описана сфера. Найти отношение объемов призмы и шара, ограниченного сферой, описанной около данной призмы.

Воспользовавшись формулой (2), выразим объем шара, ограниченного описанной около призмы сферой, через высоту и ребро основания призмы:

Ответ.

Следствие 7. Отношение объема правильной треугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Следствие 8. Отношение объема правильной четырехугольной призмы правильной четырехугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Следствие 9. Отношение объема правильной шестиугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Радиус описанной сферы и ребро «A» треугольной призмы

Видео:Геометрия Найдите площадь боковой поверхности правильной треугольной призмы, описанной околоСкачать

Свойства

Зная радиус сферы, описанной вокруг правильной треугольной призмы с равносторонним треугольником в основании, можно найти сторону этого основания и затем посчитать высоту основания, радиусы вписанной и описанной окружностей около него, а также площадь. a=√(6/5) R_1 h=a/√2=√(3/5) R_1 r=a/(2√3)=2√(2/5) R_1 R=a/√3=√(2/5) R_1 S=(√3 a^2)/4=(3√3 〖R_1〗^2)/10

Боковое ребро треугольной призмы в совокупности с радиусом описанной сферы позволяет вычислить диагональ боковой стороны, периметр призмы и площадь боковой, а затем и полной поверхности призмы. d=√(a^2+b^2 )=√(6/5 〖R_1〗^2+b^2 ) P=3(2a+b)=3(2√(6/5) R_1+b) S_(б.п.)=3ab=3b√(6/5) R_1 S_(п.п.)=3b√(6/5) R_1+(3√3 〖R_1〗^2)/5

Чтобы найти объем треугольной призмы через радиус описанной сферы и боковое ребро, нужно подставить в формулу объема необходимое выражение вместо площади основания и умножить его на боковое ребро. V=S_(осн.) b=(3√3 〖R_1〗^2)/10 b

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Сферы, описанные около многогранников.
методическая разработка по геометрии по теме

Сферы, описанные около многогранников.u

Видео:Радиус описанной окружностиСкачать

Скачать:

Предварительный просмотр:

Видео:8 класс, 39 урок, Описанная окружностьСкачать

Подписи к слайдам:

Сферы, описанные около многогранников.

Определение. Многогранник называется вписанным в сферу (а сфера описанной около многогранника), если все вершины многогранника принадлежат этой сфере. Следствие . Центр описанной сферы есть точка, равноудаленная от всех вершин многогранника. O O O . . .

Теорема 1. Множество точек равноудаленных от двух данных точек, есть плоскость, перпендикулярная к отрезку с концами в данных точках, проходящая через его середину (плоскость серединных перпендикуляров к этому отрезку). AB ┴ α AO=OB α A B O

Теорема 2. Множество точек, равноудаленных от n заданных точек, лежащих на одной окружности, есть прямая, перпендикулярная плоскости этих точек, проходящая через центр описанной около них окружности. C E A B D O a . . . . . . C E A B D . . . . .

Призма вписанная в сферу. OA=OB=…=OX=R сф . O 1 . O . O сф a 1 a .A 1 .B 1 .C 1 .D 1 E 1 . X 1 . .A .B .C .D E. X. a a 1 . O . O 1

Следствия. 1)Около прямой треугольной призмы можно описать сферу, т.к. около треугольника всегда можно описать окружность. 2) Около любой правильной призмы можно описать сферу, т.к. правильная призма является прямой и около правильного многогранника всегда можно описать окружность. O . O . .

Задача №1. Шар описан около призмы, в основании которой лежит прямоугольный треугольник с катетами 6 и 8. Боковое ребро призмы равно 24. Найдите Радиус шара. Дано : ∆ ABC – прямоугольный ; AC=6, BC=8, AA 1 =24. Найти : R ш = ? Решение : 1)OO 1 ┴AB 1 ; OO 1 =AA 1 =24. 2) ABC: AB=10. 3) O ш OB: R ш = O ш B=√OO ш 2 + OB 2 = = √144+25=13 Ответ : 13. О 1 О . . . R ш О ш С 1 B 1 A 1 A С B

Задача №3. Измерения прямоугольного параллелепипеда равны 2,3 и 5. Найдите радиус описанного шара. Дано :AB=a=2; BC=b=3; CC 1 =c=5. Найти : R ш = ? Решение : 1) AC 2 =a 2 +b 2 +c 2 . 2) A 1 C 2 =25+9+4=38 ( Свойство диагоналей прямоугольного параллелепипеда ) 3) A 1 C=√38; R ш = O ш C = √38 /2 Ответ : √38 /2 D 1 C 1 B 1 A 1 A B C D 5 2 3 . . . O ш

Задача №3. Сторона основания правильной треугольной призмы равна a, а боковое ребро равно 2 a . Найдите радиус описанного шара. Дано : AB=BC=AC=a, AA 1 ┴ABC ; AA 1= 2a. Найти : R ш = ? Решение : 1)AB=AO √3; AO=a/√3. 2)R ш =√ a 2 + a 2 /3=2a/ √ 3 Ответ : 2a/ √ 3 C 1 B A 1 C B 1 A O ш R ш . O O 1

Следствия. 1)Около треугольной пирамиду всегда можно описать сферу, так как около треугольника всегда можно описать окружность. 2)Около правильной пирамиды всегда можно описать сферу. 3)Если боковые ребра пирамиды равны (одинаково наклонены к основанию), то около такой пирамиды всегда можно описать сферу. *В последних двух случаях центр сферы лежит на прямой, содержащей высоту пирамиды. O . O .

Задачи (сфера, описанная около пирамиды). Около пирамиды PABC , основание которой – правильный треугольник ABC со стороной 4√3, описан шар. Боковое ребро PA перпендикулярно плоскости основания пирамиды и равно 6. Найти радиус шара. Дано : AB=BC=AC=4 √3 ; PA ┴(ABC); PA=6. Найти : R ш = ? Решение : 1) OO СФ ┴(ABC); O – центр описанной около ∆ABC окружности ; K O СФ ┴ PA; KP=AK (KO СФ Один из серединных перпендикуляров к боковому ребру PA ); O СФ – центр описанного шара. 2) OO СФ ┴(ABC); OO СФ принадлежит ( AKO ) ; PA ┴(ABC); AK принадлежит ( AKO ) ; значит KA|| OO СФ ; . O СФ . O K. P. A. B .C

Задачи (сфера, описанная около пирамиды). 3) KO c ф ┴AP; KO c ф принадлежит (AOK); AO ┴AP; AO принадлежит ( AOK ) ; значит KO c ф || AO; 4) Из (2) и (3) : AOO c ф K- прямоугольник, AK=PA/2=3; 5) AO=AB/ √3 =4; 6) ∆ AO O c ф : AO c ф = R ш =5 Ответ : 5

Задачи (сфера, описанная около пирамиды). В правильной четырехугольной пирамиде боковое ребро наклонено к основанию под углом 45 ˚ . Высота пирамиды равна h . Найдите радиус описанной сферы. Дано : PABCD – правильная пирамида ; (AP^(ABC))=45 ˚; PO=h . Найти : R ш = ? Решение : 1) AO=OP=h; AP=h √ 2; 2) ∆PAP 1 – прямоугольный ; PP 1 – диаметр шара ; PP 1 = 2 R ш ; AP 2 = PP 1 *OP; ( h √ 2) 2 =2 R ш *h; R ш = 2h 2 /2h=h. Ответ : h . C . B A. .D .P .P 1 . O

Задачи (сфера, описанная около пирамиды) . Самостоятельно. Радиус сферы, описанной около правильного тетраэдра равен R . Найдите площадь полной поверхности тетраэдра.

Задачи (сфера, описанная около пирамиды). Самостоятельно. Дано : DABC – правильный тетраэдр ; R – радиус сферы. Найти : S полн.тетр . =? Решение : 1) Так как тетраэдр правильный, то центр описанной сферы принадлежит прямой, содержащей высоту пирамиды ; 2) S полн.тетр . = a 2 √ 3/4*4= a 2 √ 3; 3) Точки D, A, D 1 принадлежат одной окружности – сечению сферы плоскостью DAD 1 , значит угол DAD 1 — вписанный угол, опирающийся на диаметр, DD 1 ; угол DAD 1 =90 ˚; 4) AO – высота ∆ ADD 1 , проведенная из вершины прямого угла. AD 2 = DO*DD 1 ; 5) AO=a/ √ 3; DO= √ a 2 -a 2 /3=a √ 2 / √ 3; a 2 = a √ 2 / √ 3*2R; a= √ 2 / √ 3*2R; a 2 = 8R 2 /3; .D 1 .D .O .B .C A. a a

Задачи (сфера, описанная около пирамиды). Самостоятельно. 6) S полн.тетр . = 8R 2 √ 3/3 Ответ : 8R 2 √ 3/3

📹 Видео

найти радиус окружности, описанной вокруг треугольникаСкачать

Свойство окружности, описанной около равнобедренного треугольникаСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Построить описанную окружность (Задача 1)Скачать

Вычисление радиуса сферы, описанной около правильной треугольной пирамидыСкачать

Окружность, описанная около треугольника. Как найти центр и радиус. Геометрия 7-8 классСкачать

Быстро находим радиус описанной сферыСкачать

9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Квадрат в окружности или окружность в квадрате #ShortsСкачать

Радиус описанной окружности трапецииСкачать

Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Вписанная и описанная около равнобедренного треугольника, окружностьСкачать