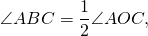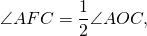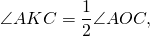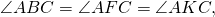Вписанные и центральные углы Вписанные и центральные углы |
 Углы, образованные хордами, касательными и секущими Углы, образованные хордами, касательными и секущими |
 Доказательства теорем об углах, связанных с окружностью Доказательства теорем об углах, связанных с окружностью |
Видео:Вписанные углы в окружностиСкачать

Вписанные и центральные углы
Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).
Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Теоремы о вписанных и центральных углах
| Фигура | Рисунок | Теорема | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | ||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же дугу равны. | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр | |||||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника |  |
| Вписанный угол | |||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника | |||||||||||||||||||||||||||||||||
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами |  |  | |
| Угол, образованный секущими, которые пересекаются вне круга |  |  | |
| Угол, образованный касательной и хордой, проходящей через точку касания |  |  | |
| Угол, образованный касательной и секущей |  |  | |
| Угол, образованный двумя касательными к окружности |  |  |
| Угол, образованный пересекающимися хордами хордами |
 |
Формула:  |
| Угол, образованный секущими секущими , которые пересекаются вне круга |
Формула:  |
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный касательной и хордой хордой , проходящей через точку касания |
 |
Формула:  |
| Угол, образованный касательной и секущей касательной и секущей |
Формула:  |
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный двумя касательными касательными к окружности |
Формулы:  |
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Видео:№655. Центральный угол АОВ на 30° больше вписанного угла, опирающегося на дугу АВ. НайдитеСкачать 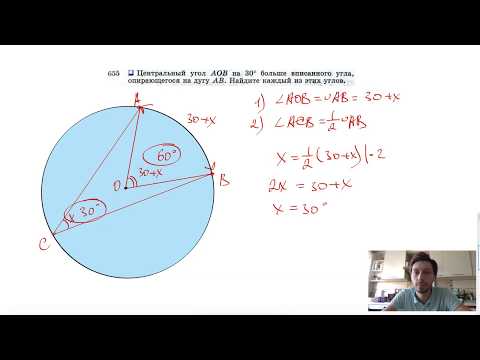 Доказательства теорем об углах, связанных с окружностьюТеорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5). Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана. Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6). В этом случае справедливы равенства и теорема 1 в этом случае доказана. Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7). В этом случае справедливы равенства что и завершает доказательство теоремы 1. Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 8. Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 9. Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами. Доказательство . Рассмотрим рисунок 10. Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства что и требовалось доказать Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 11. Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства что и требовалось доказать. Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 12. Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство Видео:Углы, вписанные в окружность. 9 класс.Скачать  Верно ли что вписанные углы опирающиеся на дугу окружности равныКакие из следующих утверждений верны? 1) Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны. 2) Если радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 3, то эти окружности не имеют общих точек. 3) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются. 4) Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°. Если утверждений несколько, запишите их номера в порядке возрастания. Проверим каждое из утверждений. 1) «Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.» — неверно, вписанные углы, опирающиеся на одну и ту же хорду окружности, равны, если их вершины лежат по одну сторону от хорды. 2) «Если радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 3, то эти окружности не имеют общих точек.» — неверно, окружности имеют две общие точки. 3) «Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются.» — верно, если расстояние от центра окружности до прямой меньше радиуса, то прямая и окружность имеют две общие точки. 4) «Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.» — верно, вписанный угол измеряется половиной дуги,на которую он опирается. Видео:Вписанный угол, опирающийся на хорду, равную радиусу окружностиСкачать  Вписанные углы, опирающиеся на одну дугуВписанные углы, опирающихся на одну дугу (или на одну хорду), обладают полезным свойством, вытекающим из теоремы о вписанном угле. Следствие из теоремы о вписанном угле. Вписанные углы, опирающиеся на одну дугу (или на одну хорду), равны. вписанный угол равен половине соответствующего ему центрального угла. Отсюда, любой вписанный угол, опирающийся на дугу AC, равен половине центрального угла AOC (или половине дуги AC). Что и требовалось доказать. Это свойство вписанных углов очень часто используется при решении задач. Позже мы рассмотрим несколько таких задач. 🎬 ВидеоВсё про вписанные и центральные углы за 4 минуты | Борис Трушин |Скачать  Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать  Геометрия. Теорема о вписанном углеСкачать  8 класс, 34 урок, Теорема о вписанном углеСкачать  Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать  Решение задач на тему центральные и вписанные углы.Скачать  Вписанный угол, опирающийся на диаметр окружности ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать  Геометрия 8 класс (Урок№26 - Градусная мера дуги окружности. Центральные углы.)Скачать  Угол, опирающийся на диаметр окружности, прямой. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать  №1 из ЕГЭ 2023 по математике. Лайфхаки для №16. Окружность, вписанные углы, хорды, касательныеСкачать  Занятие 7. Окружность. Центральные и вписанные углы. Планиметрия для ЕГЭ и ОГЭСкачать  ЦЕНТРАЛЬНЫЙ угол ВПИСАННЫЙ угол окружности 8 класс АтанасянСкачать  20 задание ОГЭ. 11429875. Анализ геометрических высказыванийСкачать  16 задание ОГЭ математика 2023 | УмскулСкачать  |