Числовая окружность положительные и отрицательные четверти (8 видео)

Четверть числовой окружности

Если посмотреть на числовую окружность , то можно заметить, что оси абсцисс и ординат разбивают ее на четыре части. Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).

(() (frac) (;2π)) — четвертая четверть

Содержание

Почему так важно определять какой четверти принадлежит угол?
Про непостоянство четвертей:
Тригонометрия простыми словами
Значения тригонометрических функций для первой четверти круга (0° – 90°)
Принцип повтора знаков тригонометрических функций
Тригонометрический круг
Углы в радианах
Тригонометрический круг: вся тригонометрия на одном рисунке
А теперь подробно о тригонометрическом круге:
🔥 Видео

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Почему так важно определять какой четверти принадлежит угол?

Дело в том, что каждая четверть уникальна в плане знаков тригонометрических функций .

Например, для любого угла из второй четверти — синус положителен, а косинус , тангенс и котангенс отрицательны. А для любого угла из первой четверти — все четыре функции будут положительны.

Теперь давайте рассмотрим пример задачи, которую не решить без использования знаний про четверти.

Пример (ЕГЭ):

Нам известен косинус, а найти нужно синус того же угла. Какая тригонометрическая формула связывает синус и косинус того же угла?
Основное тригонометрическое тождество. Запишем его.

Подставим известное, и проведем вычисления.

Видео:Тригонометрическая окружность. Как выучить?Скачать

Про непостоянство четвертей:

Важно понимать, что, например, первой четверти принадлежат не только углы от (0) до (frac) , но и углы от (2π) до (frac) , и от (4π) до (frac) , и от (6π) до (frac) и так далее. Ведь как только мы заканчиваем полный оборот – кончается четвертая четверть и опять начинается первая.

Кроме того, нужно помнить, что углы могут откладываться в отрицательную сторону (по часовой стрелке), и тогда мы попадем в первую четверть только в конце круга. Ведь сначала мы пройдем четвертую четверть, потом в третью и т.д.

Числовая окружность положительные и отрицательные четверти

((0;-) (frac) ()) — четвертая четверть

Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную.

Видео:Как искать точки на тригонометрической окружности.Скачать

Тригонометрия простыми словами

Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».

Тригонометрические функции связаны с соотношениями сторон в прямоугольном треугольнике:

Синус угла – отношение противолежащего катета к гипотенузе;
Косинус угла – отношение прилежащего катета к гипотенузе;
Тангенс угла – отношение противолежащего катета к прилежащему;
Котангенс угла – отношение прилежащего катета к противолежащему.

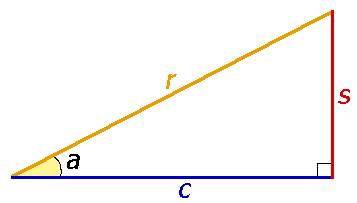Или в виде формул:

Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).

Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.

Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.

Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.

Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.

Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.

Значения тригонометрических функций
для первой четверти круга (0° – 90°)

0°

30°

45°

60°

90°

sin

√3

–

ctg

–

√3

Принцип повтора знаков тригонометрических функций

Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону.

В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ.

Например, значения тригонометрических функций для углов 270° и -90° равны.

Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно.

Видео:Алгебра 10 класс. 15 сентября. Числовая окружность #1Скачать

Тригонометрический круг

Углы в радианах

Для математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2 π r. Следовательно 360° в радианах равно 2 π , а 180° равно π радиан.

Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π .

Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.

Видео:Числовая окружностьСкачать

Тригонометрический круг: вся тригонометрия на одном рисунке

Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.

Вот что мы видим на этом рисунке:

Перевод градусов в радианы и наоборот. Полный круг содержит градусов, или радиан.

Значения синусов и косинусов основных углов. Помним, что значение косинуса угла мы находим на оси , а значение синуса — на оси .

И синус, и косинус принимают значения от до .

Значение тангенса угла тоже легко найти — поделив на . А чтобы найти котангенс — наоборот, косинус делим на синус.

Знаки синуса, косинуса, тангенса и котангенса.

Синус — функция нечётная, косинус — чётная.

Тригонометрический круг поможет увидеть, что синус и косинус — функции периодические. Период равен .

Видео:Числовая окружность | Алгебра 10 класс #8 | ИнфоурокСкачать

А теперь подробно о тригонометрическом круге:

Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.

Мы отсчитываем углы от положительного направления оси против часовой стрелки.

Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.

Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Всё это легко увидеть на нашем рисунке.

Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :

Простым следствием теоремы Пифагора является основное тригонометрическое тождество:

Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).

Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.

Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.

Легко заметить, что

Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:

где — целое число. То же самое можно записать в радианах:

Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,