Поворот окружности по часовой стрелке (7 видео)

Угол поворота, угол произвольной величины

Среди множества терминов тригонометрии важным является понятие угла поворота. В данной статье рассмотрим поворот и все соответствующие ему определения; дадим представление о полном обороте; изучим угол поворота и его характеристики, а также поворот фигуры вокруг точки. Для лучшего понимания теория будет снабжена иллюстрациями и практическими примерами.

Содержание

Поворот точки вокруг точки
Полный оборот
Угол поворота
Направление поворота
Величина угла поворота, угол произвольной величины
Поворот фигуры вокруг точки на угол
Поворот. Задачи
§ 2. Параллельный перенос и поворот
Параллельный перенос
Поворот
Задачи
🔍 Видео

Видео:Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

Поворот точки вокруг точки

Центр поворота – точка, относительно которой осуществлен поворот.

Рассмотрим, что происходит в результате поворота точки. Пусть некоторая точка А поворачивается относительно центра поворота О , в результате чего получается точка А 1 (при совершении некоторого количества полных оборотов она может совпасть с точкой А ). При этом точка А 1 лежит на окружности с центром в точке О радиуса О А . Другими словами, когда точка А осуществляет поворот относительно точки О , она переходит в точку А 1 , лежащую на окружности с центром О радиуса О А .

Считается, что в данном случае точка О при осуществлении поворота вокруг самой себя переходит в саму себя. Или: когда точка О осуществляет поворот вокруг центра поворота О , она переходит в саму себя.

Отметим также, что поворот точки А относительно центра О нужно рассматривать, в том числе, как перемещение в результате движения точки А по окружности с центром в точке О радиуса О А .

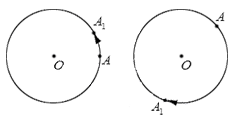
Изобразим графически поворот точки А относительно точки О , перемещение точки А в точку А 1 отметим стрелкой:

Видео:Геометрия 9 класс (Урок№30 - Поворот.)Скачать

Полный оборот

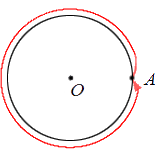
Возможно осуществить поворот точки А относительно центра поворота О таким образом, что точка А , пройдя все точки окружности, вернется на прежнее свое место. Тогда говорим, что точка совершила полный оборот вокруг точки О .

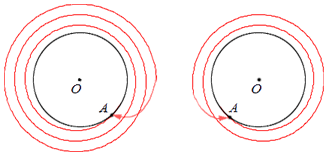
Если движение точки А по окружности продолжится, то будет выполнено два, три и так далее полных оборотов. На иллюстрации ниже справа отображено два полных оборота, а слева – три:

В рамках всего вышесказанного можно также говорить о частях полного оборота. Например, о половине оборота или трети, или четверти и так далее.

Видео:Поворот фигуры. Построить поворот фигур вокруг точки на угол по часовой или против часовой стрелкиСкачать

Угол поворота

Из указанного выше понятия поворота точки очевидно, что возможно бесконечное множество вариаций поворота точки А относительно центра О . Любую точку окружности с центром О можно рассматривать как точку А 1 , полученную в результате поворота точки А . Поэтому для определения отличия одного поворота от другого вводится понятие угла поворота.

Угол поворота имеет свои характеристики, одна из которых – направление поворота. По нему определяют, как перемещалась точка – по часовой стрелке или против.

Еще одной характеристикой угла поворота служит его величина. Углы поворота имеют ту же единицу измерения, что и углы в геометрии: наиболее распространены градусы и радианы. Отметим, что угол поворота может выражаться в градусах любым действительным числом в промежутке от — ∞ до + ∞ , что отличает его от угла в геометрии, который выражается только положительным числом, не превосходящим 180 ° .

Чтобы обозначить углы поворота, стандартно используют буквы греческого алфавита: α , β , γ и так далее. Чтобы обозначить большое количество углов поворота, применяют одну и ту же букву с различными нижними индексами: α 1 , α 2 , α 3 … . . α n .

Разберем характеристики угла поворота подробнее.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Направление поворота

Отметим на окружности с центром О точки А и А 1 . В точку А 1 возможно попасть, совершив точкой А поворот относительно центра О либо по часовой стрелке, либо – против. Очевидно определять эти повороты, как различные.

Принято считать, что поворот по часовой стрелке – поворот в отрицательном направлении направлении, а поворот против часовой стрелки – поворот в положительном направлении.

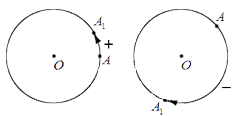
Приведем графическую иллюстрацию различных поворотов: слева на чертеже – поворот в положительном направлении; справа – в отрицательном.

Видео:Вращение против часовой стрелки.Скачать

Величина угла поворота, угол произвольной величины

Угол поворота точки, не являющейся центром поворота, в полной мере определяется указанием его величины. С другой стороны, по величине угла поворота можно определить, каким образом поворот был осуществлен.

Как было сказано выше, величина угла поворота варьируется в пределах от — ∞ до + ∞ ;

Знак плюс определяет поворот против часовой стрелки, а минус – по часовой стрелке.

Необходимо установить соответствие между самой величиной угла поворота и тем, какому повороту она соответствует.

Пусть угол поворота равен 0 ° . Такому углу поворота соответствует перемещение точки в саму себя. Иначе говоря, при повороте вокруг точки О на 0 ° точка A остается на месте.

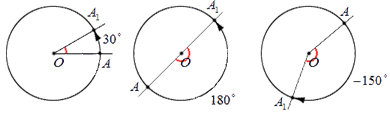
Теперь предположим, что поворот точки А происходит в пределах половины оборота: пусть точка А переходит в точку А 1 . В таком случае абсолютная величина угла А О А 1 , выраженная в градусах, не превосходит 180 . Если поворот имел положительное направление, то величина угла поворота считается равной величине угла А О А 1 ; если отрицательное – величина угла поворота равна величине угла А О А 1 со знаком минус. Для иллюстрации этих утверждений отобразим на чертеже углы поворота в 30 ° , 180 ° и — 150 ° :

Углы поворота, превышающие 180 или меньшие – 180 определяются, исходя из очевидного свойства последовательных поворотов:

Несколько последовательных поворотов точки А относительно центра О равносильны одному повороту, величина которого равна сумме величин этих поворотов.

Рассмотрим пример, который даст нам возможность графически проиллюстрировать описанное свойство. Пусть точка А выполняет поворот относительно центра О на 45 ° , затем еще на 60 ° и еще раз — на — 35 ° . Обозначим промежуточные точки поворотов А 1 , А 2 и А 3 . В конечную точку А 3 возможно было попасть, совершив один поворот на угол поворота, величина которого равна: 45 ° + 60 ° + ( — 35 ° ) = 70 ° . Проиллюстрируем:

Таким, образом, углы, превышающие 180 ° , будем представлять, как несколько последовательных поворотов на углы, сумма величин которых определяет величину исходного угла поворота. Например, угол поворота 298 ° соответствует последовательным поворотам на 180 ° и 118 ° , или 90 ° , 90 ° , 90 ° и 28 ° , или 180 ° , 180 ° и — 62 ° , или 298 последовательных поворотов на 1 ° .

По такому же принципу определяются углы меньше — 180 ° . Например, угол поворота — 515 ° можно определить, как последовательные повороты на — 180 ° , — 180 ° и — 155 ° .

Нами был определен угол поворота, и его величина выражается в градусах некоторым действительным числом в пределах от — ∞ до + ∞ . Тригонометрия работает именно с углами поворота, хотя для удобства слово «поворот» опускают и говорят «угол». Т.е. будем рассматривать углы произвольной величины, понимая под ними углы поворота.

В заключение также отметим, что полный оборот в положительном направлении соответствует углу поворота в 360 ° или 2 π радиан. Соответственно при отрицательном направлении полный оборот будет соответствовать углу в — 360 ° или — 2 π радиан.

При этом удобно большие углы поворота представлять, как некоторое количество полных оборотов и еще один на величину в пределах от — 180 ° до 180 ° . К примеру, поворот осуществляется на 1478 ° . Представим эту величину как: 360 · 4 + 38 , т.е. заданному углу поворота соответствуют 4 полных оборота и еще один поворот – на 38 ° . Или еще один пример: угол поворота в — 815 ° можно представить, как ( — 360 ) · 2 + ( — 95 ) , т.е. заданному углу поворота соответствуют 2 полных оборота в отрицательном направлении (против часовой стрелки) и еще один поворот того же направления на — 95 ° .

Видео:Шарик равномерно движется по окружности по часовой стрелке на горизонтальной поверхности - №27354Скачать

Поворот фигуры вокруг точки на угол

Понятие поворота точки легко распространить на поворот любой фигуры вокруг точки на угол (такой поворот, при котором и точка, относительно которой осуществляется поворот, и сама поворачиваемая фигура лежат в одной плоскости).

Поворот фигуры – это поворот всех ее точек вокруг заданной точки на заданный угол.

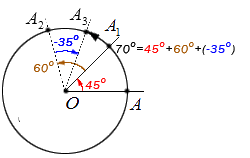
Как пример, иллюстрируем следующее действие: поворот отрезка А В на угол α относительно точки О – при повороте заданный отрезок перейдет в отрезок А 1 В 1 .

Видео:Пошаговая схема поворота на 150° против часовой стрелки.Скачать

Поворот. Задачи

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Это занятие будет посвящено теме «Поворот». Мы решим несколько задач на упомянутую тему, но для начала повторим понятие движения. После чего рассмотрим один из видов движения – поворот, перечислим его свойства и особенности. Решим вместе с преподавателем задачи на эту тему.

Если у вас возникнет сложность в понимании тему, рекомендуем посмотреть урок «Связь числа и геометрии. Часть 1. Измерения в геометрии. Свойства фигур»

Видео:Решение задач по теме "Поворот точки вокруг начала координат"Скачать

§ 2. Параллельный перенос и поворот

Параллельный перенос

Пусть — данный вектор. Параллельным переносом на вектор называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М₁, что вектор равен вектору (рис. 329).

Параллельный перенос является движением, т. е. отображением плоскости на себя, сохраняющим расстояния. Докажем это. Пусть при параллельном переносе на вектор точки М и N отображаются в точки М₁ и N₁ (см. рис. 329). Так как , то . Отсюда следует, что ММ₁ || NN₁ и MM₁ = NN₁, поэтому четырёхугольник MM₁N₁N — параллелограмм. Следовательно, MN = M₁N₁, т. е. расстояние между точками М и N равно расстоянию между точками М₁ и N₁ (случаи, когда точки М и N расположены на прямой, параллельной вектору , рассмотрите самостоятельно). Таким образом, параллельный перенос сохраняет расстояния между точками и поэтому представляет собой движение. Наглядно это движение можно представить себе как сдвиг всей плоскости в направлении данного вектора на его длину.

Поворот

Отметим на плоскости точку О (центр поворота) и зададим угол а (угол поворота). Поворотом плоскости вокруг точки О на угол α называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М₁, что ОМ = ОМ₁ и угол МОМ₁ равен α (рис. 330). При этом точка О остаётся на месте, т. е. отображается сама в себя, а все остальные точки поворачиваются вокруг точки О в одном и том же направлении — по часовой стрелке или против часовой стрелки. На рисунке 330 изображён поворот против часовой стрелки.

Поворот является движением, т. е. отображением плоскости на себя, сохраняющим расстояния.

Докажем это. Пусть О — центр поворота, α — угол поворота против часовой стрелки (случай поворота по часовой стрелке рассматривается аналогично). Допустим, что при этом повороте точки М и N отображаются в точки М₁ и N₁ (рис. 331). Треугольники OMN и ОМ₁N₁ равны по двум сторонам и углу между ними: ОМ = ОМ₁, ON = ON₁ и ∠MON = ∠M₁ON₁ (для случая, изображённого на рисунке 331, каждый из этих углов равен сумме угла α и угла M₁ON). Из равенства этих треугольников следует, что MN = M₁N₁, т. е. расстояние между точками М и N равно расстоянию между точками М, и N, (случай, когда точки О, М и N расположены на одной прямой, рассмотрите самостоятельно). Итак, поворот сохраняет расстояния между точками и поэтому представляет собой движение. Это движение можно представить себе как поворот всей плоскости вокруг данной точки О на данный угол α.

Задачи

1162. Начертите отрезок АВ и вектор . Постройте отрезок А1В1, который получается из отрезка АВ параллельным переносом на вектор .

1163. Начертите треугольник АВС, вектор , который не параллелен ни одной из сторон треугольника, и вектор , паралдельный стороне АС. Постройте треугольник А₁В₁С₁, который получается из треугольника АВС параллельным переносом: а) на вектор ; б) на вектор .

1164. Даны равнобедренный треугольник АВС с основанием АС и такая точка D на прямой АС, что точка С лежит на отрезке AD. а) Постройте отрезок BlD, который получается из отрезка ВС параллельным переносом на вектор . б) Докажите, что четырёхугольник ABB₁D — равнобедренная трапеция.

1165. Даны треугольник, трапеция и окружность. Постройте фигуры, которые получаются из этих фигур параллельным переносом на данный вектор .

1166. Постройте отрезок А₁В₁, который получается из данного отрезка АВ поворотом вокруг данного центра О: а) на 120° по часовой стрелке; б) на 75° против часовой стрелки; в) на 180°.

1167. Постройте треугольник, который получается из данного треугольника АВС поворотом вокруг точки А на угол 150° против часовой стрелки.

1168. Точка D является точкой пересечения биссектрис равностороннего треугольника АВС. Докажите, что при повороте вокруг точки D на угол 120° треугольник АВС отображается на себя.

1169. Докажите, что при повороте квадрата вокруг точки пересечения его диагоналей на угол 90° квадрат отображается на себя.

1170. Постройте окружность, которая получается из данной окружности с центром С поворотом вокруг точки О на угол 60° против часовой стрелки, если: а) точки О и С не совпадают; б) точки О и С совпадают.

1171. Постройте прямую а₁, которая получается из данной прямой а поворотом вокруг точки О на угол 60° по часовой стрелке, если прямая а: а) не проходит через точку О; б) проходит через точку О.

а) Построим окружность с центром О, которая касается прямой а (объясните, как это сделать). Пусть М — точка касания. При повороте вокруг точки О эта окружность отображается на себя, а касательная а отображается на некоторую касательную а₁ (объясните почему). Для построения прямой ах построим сначала точку М₁, в которую отображается точка М при повороте вокруг точки О на угол 60° по часовой стрелке, а затем проведём касательную а₁ к окружности в точке М₁.