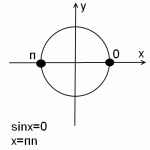Sinx 0 на окружности решение (8 видео) | Курс школьной геометрии

Узнать ещё

Знание — сила. Познавательная информация

Содержание

sinx=0
Тригонометрические уравнения с модулем
📸 Видео

Видео:Отбор корней по окружностиСкачать

sinx=0

Эта ассоциация позволяет легко запомнить, где синус равен 0, и быстро решить уравнение sin x=0.

Как обычно, частные случаи синуса рассматриваем на единичной окружности.

Используем ассоциацию косинус-колобок. Оба начинаются с ко-, в названии cos x буква o тоже косвенно на колобка указывает. Колобок движется по горизонтали. На координатной плоскости движение по горизонтали происходит вдоль оси x.

Поэтому cos x — это x, соответственно, sin x — это y.

Таким образом, чтобы найти, где синус равен 0, нужно выяснить, в каких точках y=0.

Раз y=0, то движения вверх-вниз не происходит.

На единичной окружности условию sin x=0 удовлетворяют две точки: 0 и π.

Чтобы из одной точки попасть в другую, надо пройти половину окружности, то есть π.

Поскольку таких точек, в которых синус равен 0, бесконечное множество, прибавляем не π, а πn, где n — целое число (то есть n принадлежит Z): x=0+πn.

Следовательно, решение уравнения sin x=0, есть множество точек

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Простейшими тригонометрическими уравнениями называют уравнения

Чтобы рассуждения по нахождению корней этих уравнений были более наглядными, воспользуемся графиками соответствующих функций.

19.1. Уравнение cos x = a

Объяснение и обоснование

Корни уравненияcosx=a.

2.Частые случаи решения уравнения sin x = a.

Полезно помнить специальные записи корней уравнения при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность (рис 2).

Учитывая, что синус равен ординате соответствующей точки единичной окружности, получаем, что sin x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C или тока D. Тогда

Аналогично sin x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка A, следовательно,

Также sin x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка B, таким образом,

Примеры решения задач

Замечание. Ответ к задаче 1 часто записывают в виде:

19.3. Уравнения tg x = a и ctg x = a

Объяснение и обоснование

1.Корни уравнений tg x = a и ctg x = a

Рассмотрим уравнение tg x = a. На промежутке функция y = tg x возрастает (от -∞ до +∞). Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение tg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арктангенса равен: x₁ = arctg a и для этого корня tg x = a.

Функция y = tg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения tg x = a:

При a=0 arctg 0 = 0, таким образом, уравнение tg x = 0 имеет корни x = πn (n ∈ Z).

Рассмотрим уравнение ctg x = a. На промежутке (0; π) функция y = ctg x убывает (от +∞ до -∞). Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x₁=arсctg a.

Функция y = ctg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения ctg x = a:

таким образом, уравнение ctg x = 0 имеет корни

Примеры решения задач

Вопросы для контроля

Какие уравнения называют простейшими тригонометрическими?
Запишите формулы решения простейших тригонометрических уравнений. В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам?
Выведите формулы решения простейших тригонометрических уравнений.
Обоснуйте формулы решения простейших тригонометрических уравнений для частных случаев.

Упражнения

Решите уравнение (1-11)

Найдите корни уравнения на заданном промежутке (12-13)

Видео:Решить тригонометрические неравенства sinxСкачать

Тригонометрические уравнения с модулем

Разделы: Математика

Раскрытие модуля по определению

Модулем числа а называется само это число а, если а ≥ 0, и число -а, если а 2 x-sinx=0

sinx=0 или sinx= (оба уравнения удовлетворяют условию sinx≥0)

Решаем уравнение второй системы, и выбирая те, которые удовлетворяют условию sinx 2

cosx=0 или x+1,5=1 или x-1,5 = -1

х= -0,5 х = -2,5

Условию cosx≥0 не удовлетворяет х = -2,5 (3 четверть)

Ответ:

№5. Найти все решения уравнения на отрезке [0;4].

Решение. Перепишем уравнение в виде

Раскрывая знак модуля, получаем системы:

Решая первую систему, получим

Из серии в нужном промежутке [0;4] лежат точки 0 и ; , а из серии

Решая вторую систему, получим систему , которая не имеет решений.

Ответ:

№6 Решить уравнение.

Решение. Правая часть уравнения неотрицательна, значит, неотрицательна и левая часть, тогда 2х-4≥0, 2(х-2)≥0 , х-2≥0. Если х-2≥0. то при раскрытия правого модуля по определению рассматривается только один случай:

х=2

Выберем те корни, которые удовлетворяют условию: х-2≥0; х≥2

№7. Решить уравнение.

Решение. ОДЗ:

Раскрывая знак модуля, получаем системы:

Решая первую систему, получим cos2x=0, и из решений надо выбрать те, при которых sinx>0. На круге видно, что это точки вида

Решая вторую систему, получим уравнение соs2x=2,не имеющее решений.

Ответ:

№8. Решить уравнение.

Решение. Преобразуем уравнение следующим образом:

Ответ:

№9. Решить уравнение.

Решение. Выражение под первым модулем всегда неотрицательно, и его можно сразу отбросить. Второй модуль раскрываем по определению.

Решить уравнение первой система аналитически невозможно, исследуем поведение левой и правой частей на данных промежутках. Функция f(x) =-x 2 +15x-45=(-x 2 +15x-44)-1≤-1

при причем, f(х)= -1 в точках 4 и 11.Левая часть cos при любых х, причем, в точках 4 и 11 не равна -1, значит, система решений не имеет.