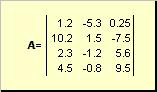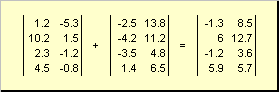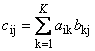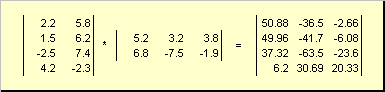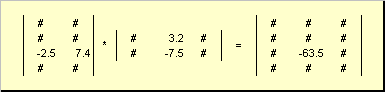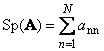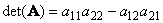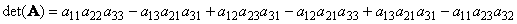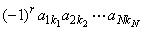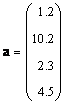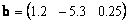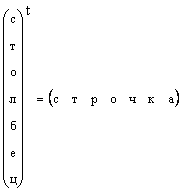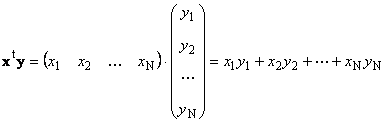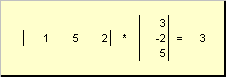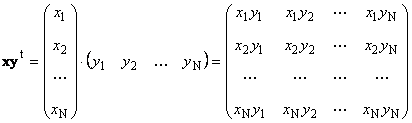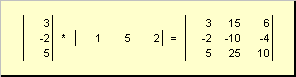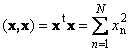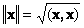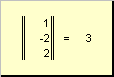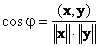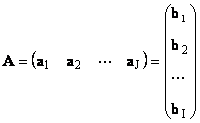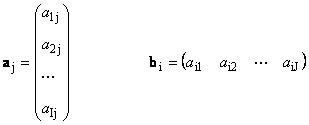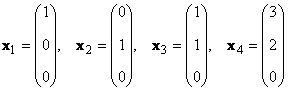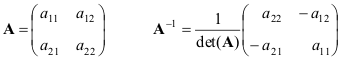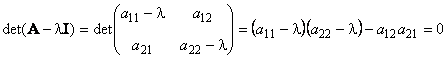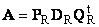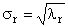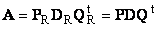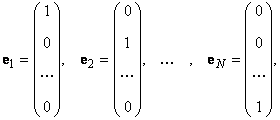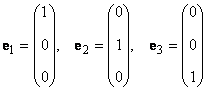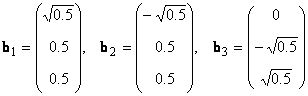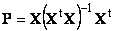Отличие вектора от матрицы

В этом документе собраны основные сведения из алгебры матриц и векторов, которые используются в хемометрике. Приведенный текст не может служить учебником по матричной алгебре — он скорее является конспектом, справочником в этой области. Более глубокое и систематическое изложение может быть найдено в литературе.

Текст разбит на две части названные — «Базовые сведения» и «Дополнительная информация». В первой части изложены положения, минимально необходимые для понимания хемометрики, а во второй части — факты, которые необходимо знать для более глубокого постижения методов многомерного анализа. Изложение иллюстрируется примерами, выполненными в рабочей книге Excel Matrix.xls, которая сопровождает этот документ.

Ссылки на примеры помещены в текст как объекты Excel. Эти примеры имеют абстрактный характер, они никак не привязаны к задачам аналитической химии. Реальные примеры использования матричной алгебры в хемометрике рассмотрены в других текстах, посвященных разнообразным хемометрическим приложениям.

Большинство измерений, проводимых в аналитической химии, являются не прямыми, а косвенными . Это означает, что в эксперименте вместо значения искомого аналита C (концентрации) получается другая величина x (сигнал), связанная, но не равная C, т.е. x (C) ≠ С. Как правило, вид зависимости x (C) не известен, однако, к счастью, в аналитической химии большинство измерений пропорциональны. Это означает, что при увеличении концентрации С в a раз, сигнал X увеличится на столько же., т.е. x ( a C) = a x (C). Кроме того, сигналы еще и аддитивны, так что сигнал от пробы, в которой присутствуют два вещества с концентрациями C 1 и C 2 , будет равен сумме сигналов от каждого компонента, т.е. x (C 1 + C 2 ) = x (C 1 )+ x (C 2 ). Пропорциональность и аддитивность вместе дают линейность . Можно привести много примеров, иллюстрирующих принцип линейности, но достаточно упомянуть два самых ярких примера — хроматографию и спектроскопию. Вторая особенность, присущая эксперименту в аналитической химии — это многоканальность . Современное аналитическое оборудование одновременно измеряет сигналы для многих каналов. Например, измеряется интенсивность пропускания света сразу для нескольких длин волн, т.е. спектр. Поэтому в эксперименте мы имеем дело со множеством сигналов x 1 , x 2 . x n , характеризующих набор концентраций C 1 ,C 2 , . C m веществ, присутствующих в изучаемой системе.

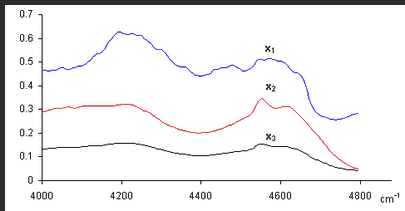
Итак, аналитический эксперимент характеризуется линейностью и многомерностью. Поэтому удобно рассматривать экспериментальные данные как векторы и матрицы и манипулировать с ними, используя аппарат матричной алгебры. Плодотворность такого подхода иллюстрирует пример, показанный на Рис. 1, где представлены три спектра, снятые для 200 длин волн от 4000 до 4796 cm −1 . Первый ( x 1 ) и второй ( x 2 ) спектры получены для стандартных образцов, в которых концентрация двух веществ A и B, известны: в первом образце [A] = 0.5, [B] = 0.1, а во втором образце [A] = 0.2, [B] = 0.6. Что можно сказать о новом, неизвестном образце, спектр которого обозначен x 3 ?

Рассмотрим три экспериментальных спектра x 1 , x 2 и x 3 как три вектора размерности 200. Средствами линейной алгебры можно легко показать, что x 3 = 0.1 x 1 +0.3 x 2 , поэтому в третьем образце очевидно присутствуют только вещества A и B в концентрациях [A] = 0.5×0.1 + 0.2×0.3 = 0.11 и [B] = 0.1×0.1 + 0.6×0.3 = 0.19.

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

1. Базовые сведения

Видео:Матрицы и векторыСкачать

1.1 Матрицы

Матрицей называется прямоугольная таблица чисел, например

Матрицы обозначаются заглавными полужирными буквами ( A ), а их элементы — соответствующими строчными буквами с индексами, т.е. a ij . Первый индекс нумерует строки, а второй — столбцы. В хемометрике принято обозначать максимальное значение индекса той же буквой, что и сам индекс, но заглавной. Поэтому матрицу A можно также записать как < a ij , i = 1. I ; j = 1. J >. Для приведенной в примере матрицы I = 4, J = 3 и a 23 = −7.5.

Пара чисел I и J называется размерностью матрицы и обознается как I × J . Примером матрицы в хемометрике может служить набор спектров, полученный для I образцов на J длинах волн.

Видео:Что такое векторы и матрицы? Душкин объяснитСкачать

1.2. Простейшие операции с матрицами

Матрицы можно умножать на числа. При этом каждый элемент умножается на это число. Например —

Рис. 3 Умножение матрицы на число

Две матрицы одинаковой размерности можно поэлементно складывать и вычитать. Например,

Рис. 4 Сложение матриц

В результате умножения на число и сложения получается матрица той же размерности.

Нулевой матрицей называется матрица, состоящая из нулей. Она обозначается O . Очевидно, что A + O = A , A − A = O и 0 A = O .

Матрицу можно транспонировать . При этой операции матрица переворачивается, т.е. строки и столбцы меняются местами. Транспонирование обозначается штрихом, A ‘ или индексом A t . Таким образом, если A = < a ij , i = 1. I ; j = 1. J >, то A t = < a ji , j = 1. J ; i = 1. I >. Например

Рис. 5 Транспонирование матрицы

Очевидно, что ( A t ) t = A , ( A + B ) t = A t + B t .

Видео:Занятие 12. Векторы и матрицыСкачать

1.3. Умножение матриц

Матрицы можно перемножать, но только в том случае, когда они имеют соответствующие размерности. Почему это так, будет ясно из определения. Произведением матрицы A , размерностью I × K , и матрицы B , размерностью K × J , называется матрица C , размерностью I × J , элементами которой являются числа

Таким образом для произведения AB необходимо, чтобы число столбцов в левой матрице A было равно числу строк в правой матрице B . Пример произведения матриц —

Рис.6 Произведение матриц

Правило перемножения матриц можно сформулировать так. Для того, чтобы найти элемент матрицы C , стоящий на пересечении i -ой строки и j -ого столбца ( c ij ) надо поэлементно перемножить i -ую строку первой матрицы A на j -ый столбец второй матрицы B и сложить все результаты. Так в показанном примере, элемент из третьей строки и второго столбца, получается как сумма поэлементных произведений третьей строки A и второго столбца B

Рис.7 Элемент произведения матриц

Произведение матриц зависит от порядка, т.е. AB ≠ BA , хотя бы по соображениям размерности. Говорят, что оно некоммутативно. Однако произведение матриц ассоциативно. Это означает, что ABC = ( AB ) C = A ( BC ). Кроме того, оно еще и дистрибутивно, т.е. A ( B + C ) = AB + AC . Очевидно, что AO = O .

Видео:Собственные значения и собственные векторыСкачать

1.4. Квадратные матрицы

Если число столбцов матрицы равно числу ее строк ( I = J = N ), то такая матрица называется квадратной. В этом разделе мы будем рассматривать только такие матрицы. Среди этих матриц можно выделить матрицы, обладающие особыми свойствами.

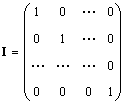
Единичной матрицей (обозначается I, а иногда E ) называется матрица, у которой все элементы равны нулю, за исключением диагональных, которые равны 1, т.е.

Очевидно AI = IA = A .

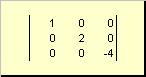
Матрица называется диагональной , если все ее элементы, кроме диагональных ( a ii ) равны нулю. Например

Рис. 8 Диагональная матрица

Матрица A называется верхней треугольной , если все ее элементы, лежащие ниже диагонали, равны нулю, т.е. a ij = 0, при i > j . Например

Рис. 9 Верхняя треугольная матрица

Аналогично определяется и нижняя треугольная матрица.

Матрица A называется симметричной , если A t = A . Иными словами a ij = a ji . Например

Рис. 10 Симметричная матрица

Матрица A называется ортогональной , если

Матрица называется нормальной если

Видео:Собственные векторы и собственные числа линейного оператораСкачать

1.5. След и определитель

Следом квадратной матрицы A (обозначается Tr( A ) или Sp( A )) называется сумма ее диагональных элементов,

Рис. 11 След матрицы

Sp(α A ) = α Sp( A ) и

Sp( A + B ) = Sp( A )+ Sp( B ).

Можно показать, что

Sp( A ) = Sp( A t ), Sp( I ) = N ,

Другой важной характеристикой квадратной матрицы является ее определитель (обозначается det( A )). Определение определителя в общем случае довольно сложно, поэтому мы начнем с простейшего варианта — матрицы A размерностью (2×2). Тогда

Для матрицы (3×3) определитель будет равен

В случае матрицы ( N × N ) определитель вычисляется как сумма 1·2·3· . · N = N ! слагаемых, каждый из которых равен

Индексы k 1 , k 2 . k N определяются как всевозможные упорядоченные перестановки r чисел в наборе (1, 2, . , N ). Вычисление определителя матрицы — это сложная процедура, которую на практике осуществляется с помощью специальных программ. Например,

Рис. 12 Определитель матрицы

Отметим только очевидные свойства:

det( I ) = 1, det( A ) = det( A t ),

det( AB ) = det( A )det( B ).

Видео:Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать

1.6. Векторы

Если матрица состоит только из одного столбца ( J = 1), то такой объект называется вектором . Точнее говоря, вектором-столбцом. Например

Можно рассматривать и матрицы, состоящие из одной строки, например

Этот объект также является вектором, но вектором-строкой . При анализе данных важно понимать, с какими векторами мы имеем дело — со столбцами или строками. Так спектр, снятый для одного образца можно рассматривать как вектор-строку. Тогда набор спектральных интенсивностей на какой-то длине волны для всех образцов нужно трактовать как вектор-столбец.

Размерностью вектора называется число его элементов.

Ясно, что всякий вектор-столбец можно превратить в вектор-строку транспонированием, т.е.

В тех случаях, когда форма вектора специально не оговаривается, а просто говорится вектор, то имеют в виду вектор-столбец. Мы тоже будем придерживаться этого правила. Вектор обозначается строчной прямой полужирной буквой. Нулевым вектором называется вектор, все элементы которого раны нулю. Он обозначается 0 .

Видео:Собственные векторы и собственные значения матрицыСкачать

1.7. Простейшие операции с векторами

Векторы можно складывать и умножать на числа так же, как это делается с матрицами. Например,

Рис. 13 Операции с векторами

Два вектора x и y называются колинеарными , если существует такое число α, что

Видео:#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy урокиСкачать

1.8. Произведения векторов

Два вектора одинаковой размерности N можно перемножить. Пусть имеются два вектора x = ( x 1 , x 2 . x N ) t и y = ( y 1 , y 2 . y N ) t . Руководствуясь правилом перемножения «строка на столбец», мы можем составить из них два произведения: x t y и xy t . Первое произведение

называется скалярным или внутренним . Его результат — это число. Для него также используется обозначение ( x , y ) = x t y . Например,

Рис. 14 Внутреннее (скалярное) произведение

называется внешним . Его результат — это матрица размерности ( N × N ). Например,

Рис. 15 Внешнее произведение

Векторы, скалярное произведение которых равно нулю, называются ортогональными .

Видео:Высшая математика. Линейные пространства. Векторы. БазисСкачать

1.9. Норма вектора

Скалярное произведение вектора самого на себя называется скалярным квадратом. Эта величина

определяет квадрат длины вектора x . Для обозначения длины (называемой также нормой вектора) используется обозначение

Рис. 16 Норма вектора

Вектор единичной длины (|| x || = 1) называется нормированным. Ненулевой вектор ( x ≠ 0 ) можно нормировать, разделив его на длину, т.е. x = || x || ( x/ || x ||) = || x || e . Здесь e = x/ || x || — нормированный вектор.

Векторы называются ортонормированными, если все они нормированы и попарно ортогональны.

Видео:Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

1.10. Угол между векторами

Скалярное произведение определяет и угол φ между двумя векторами x и y

Если вектора ортогональны, то cosφ = 0 и φ = π/2, а если они колинеарны, то cosφ = 1 и φ = 0.

Видео:Айгенвектора и айгензначения | Сущность Линейной Алгебры, глава 10Скачать

1.11. Векторное представление матрицы

Каждую матрицу A размера I × J можно представить как набор векторов

Здесь каждый вектор a j является j -ым столбцом, а вектор-строка b i является i -ой строкой матрицы A

Видео:А.7.35 Собственные вектора и собственные значения матрицыСкачать

1.12. Линейно зависимые векторы

Векторы одинаковой размерности ( N ) можно складывать и умножать на число, также как матрицы. В результате получится вектор той же размерности. Пусть имеется несколько векторов одной размерности x 1 , x 2 . x K и столько же чисел α α 1 , α 2 . α K . Вектор

y = α 1 x 1 + α 2 x 2 +. + α K x K

называется линейной комбинацией векторов x k .

Если существуют такие ненулевые числа α k ≠ 0, k = 1. K , что y = 0 , то такой набор векторов x k называется линейно зависимым . В противном случае векторы называются линейно независимыми. Например, векторы x 1 = (2, 2) t и x 2 = (−1, −1) t линейно зависимы, т.к. x 1 +2 x 2 = 0

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

1.13. Ранг матрицы

Рассмотрим набор из K векторов x 1 , x 2 . x K размерности N . Рангом этой системы векторов называется максимальное число линейно-независимых векторов. Например в наборе

имеются только два линейно независимых вектора, например x 1 и x 2 , поэтому ее ранг равен 2.

Очевидно, что если векторов в наборе больше, чем их размерность ( K > N ), то они обязательно линейно зависимы.

Рангом матрицы (обозначается rank( A )) называется ранг системы векторов, из которых она состоит. Хотя любую матрицу можно представить двумя способами (векторы столбцы или строки), это не влияет на величину ранга, т.к.

rank( A ) = rank( A t ).

Видео:7. MathCad. Векторы и матрицыСкачать

1.14. Обратная матрица

Квадратная матрица A называется невырожденной, если она имеет единственную обратную матрицу A -1 , определяемую условиями

Обратная матрица существует не для всех матриц. Необходимым и достаточным условием невырожденности является

det( A ) ≠ 0 или rank( A ) = N .

Обращение матрицы — это сложная процедура, для выполнения которой существуют специальные программы. Например,

Рис. 17 Обращение матрицы

Приведем формулы для простейшего случая — матрицы 2×2

Если матрицы A и B невырождены, то

Видео:Математика это не ИсламСкачать

1.15. Псевдообратная матрица

Если матрица A вырождена и обратная матрица не существует, то в некоторых случаях можно использовать псевдообратную матрицу, которая определяется как такая матрица A + , что

Псевдобратная матрица — не единственная и ее вид зависит от способа построения. Например для прямоугольной матрицы можно использовать метод Мура-Пенроуза.

Если число столбцов меньше числа строк, то

A + =(A t A) −1 A t

Рис. 1 7a Псевдообращение матрицы

Если же число столбцов больше числа строк, то

A + =A t (AA t ) −1

Видео:Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

1.16. Умножение вектора на матрицу

Вектор x можно умножать на матрицу A подходящей размерности. При этом вектор-столбец умножается справа Ax , а вектор строка — слева x t A . Если размерность вектора J , а размерность матрицы I × J то в результате получится вектор размерности I . Например,

Рис. 18 Умножение вектора на матрицу

Если матрица A — квадратная ( I × I ), то вектор y = Ax имеет ту же размерность, что и x . Очевидно, что

A (α 1 x 1 + α 2 x 2 ) = α 1 Ax 1 + α 2 Ax 2 .

Поэтому матрицы можно рассматривать как линейные преобразования векторов. В частности Ix = x , Ox = 0 .

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

2. Дополнительная информация

Видео:Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

2.1. Системы линейных уравнений

Пусть A — матрица размером I × J , а b — вектор размерности J . Рассмотрим уравнение

относительно вектора x , размерности I . По сути — это система из I линейных уравнений с J неизвестными x 1 . x J . Решение существует в том, и только в том случае, когда

rank( A ) = rank( B ) = R ,

где B — это расширенная матрица размерности I ×( J+1 ), состоящая из матрицы A , дополненной столбцом b , B = ( A b ). В противном случае уравнения несовместны.

Если R = I = J , то решение единственно

Если R I , то существует множество различных решений, которые можно выразить через линейную комбинацию J − R векторов. Система однородных уравнений Ax = 0 с квадратной матрицей A ( N × N ) имеет нетривиальное решение ( x ≠ 0 ) тогда и только тогда, когда det( A ) = 0. Если R = rank( A ) N , то существуют N − R линейно независимых решений.

Видео:Линал 2.6. Умножение матрицы на векторСкачать

2.2. Билинейные и квадратичные формы

Если A — это квадратная матрица , а x и y — вектора соответствующей размерности, то скалярное произведение вида x t Ay называется билинейной формой , определяемой матрицей A . При x = y выражение x t Ax называется квадратичной формой.

2.3. Положительно определенные матрицы

Квадратная матрица A называется положительно определенной, если для любого ненулевого вектора x ≠ 0 ,

Аналогично определяются отрицательно ( x t Ax x t Ax ≥ 0) и неположительно ( x t Ax ≤ 0) определенные матрицы.

2.4. Разложение Холецкого

Если симметричная матрица A положительно определена, то существует единственная треугольная матрица U с положительными элементами, для которой

Рис. 19 Разложение Холецкого

2.5. Полярное разложение

Пусть A — это невырожденная квадратная матрица размерности N × N . Тогда существует однозначное полярное представление

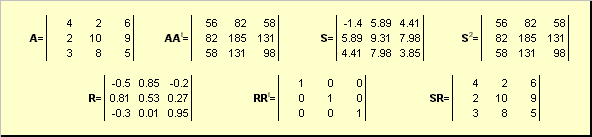
где S — это неотрицательная симметричная матрица, а R — это ортогональная матрица. Матрицы S и R могут быть определены явно:

S 2 = AA t или S = ( AA t ) ½ и R = S −1 A = ( AA t ) −½ A .

Рис. 20 Полярное разложение

Если матрица A вырождена, то разложение не единственно — а именно: S по-прежнему одна, а вот R может быть много. Полярное разложение представляет матрицу A как комбинацию сжатия/растяжения S и поворота R .

2.6. Собственные векторы и собственные значения

Пусть A — это квадратная матрица. Вектор v называется собственным вектором матрицы A , если

где число λ называется собственным значением матрицы A . Таким образом преобразование, которое выполняет матрица A над вектором v , сводится к простому растяжению или сжатию с коэффициентом λ. Собственный вектор определяется с точностью до умножения на константу α ≠ 0, т.е. если v — собственный вектор, то и α v — тоже собственный вектор.

2.7. Собственные значения

У матрицы A , размерностью ( N × N ) не может быть больше чем N собственных значений. Они удовлетворяют характеристическому уравнению

являющемуся алгебраическим уравнением N -го порядка. В частности, для матрицы 2×2 характеристическое уравнение имеет вид

Рис. 21 Собственные значения

Набор собственных значений λ 1 . λ N матрицы A называется спектром A .

Спектр обладает разнообразными свойствами. В частности

det( A ) = λ 1 ×. ×λ N , Sp( A ) = λ 1 +. +λ N .

Собственные значения произвольной матрицы могут быть комплексными числами, однако если матрица симметричная ( A t = A ), то ее собственные значения вещественны.

2.8. Собственные векторы

У матрицы A , размерностью ( N × N ) не может быть больше чем N собственных векторов, каждый из которых соответствует своему собственному значению. Для определения собственного вектора v n нужно решить систему однородных уравнений

Она имеет нетривиальное решение, поскольку det( A − λ n I ) = 0.

Рис. 22 Собственные вектора

Собственные вектора симметричной матрицы ортогональны.

2.9. Эквивалентные и подобные матрицы

Две прямоугольные матрицы A и B одной размерности I × J эквивалентны , если существуют такие квадратные матрицы S , размерности I × I , и T , размерности J × J , что

Эквивалентные матрицы имею один и тот же ранг.

Две прямоугольные матрицы A и B одной размерности N × N подобны , если существует такая невырожденная матрица T , что

Матрица T называется преобразованием подобия.

Подобные матрицы имеют один и тот же ранг, след, определитель и спектр.

2.10. Приведение матрицы к диагональному виду

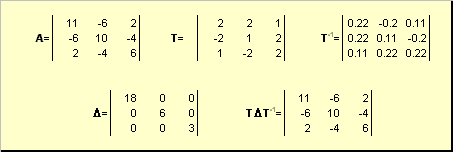
Нормальную (в частности симметричную) матрицу A можно привести к диагональному виду преобразованием подобия —

Здесь Λ = diag(λ 1 . λ N ) — это диагональная матрица, элементами которой являются собственные значения матрицы A , а T — это матрица, составленная из соответствующих собственных векторов матрицы A , т.е. T = ( v 1 . v N ).

Рис. 23 Приведение к диагональному виду

2.11. Разложение по сингулярным значениям (SVD)

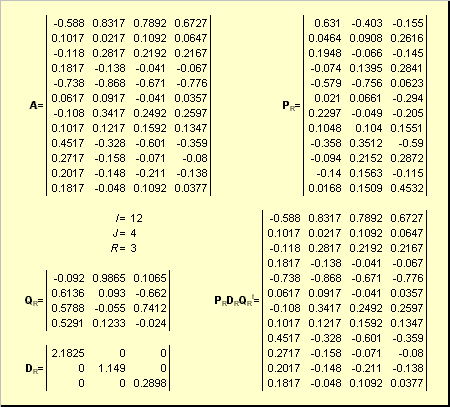
Пусть имеется прямоугольная матрица A размерностью I × J ранга R ( I ≤ J ≤ R ). Ее можно разложить в произведение трех матриц P R ( I × R ), D R ( R × R ) и Q R ( J × R ) —

.

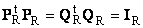
Здесь P R — матрица, образованная R ортонормированными собственными векторами p r матрицы AA t , соответствующим R наибольшим собственным значениям λ r ;

AA t p r = λ r p r ;

Q R — матрица, образованная R ортонормированными собственными векторами q r матрицы A t A ;

A t Aq r = λ r q r .

D R = diag (σ 1 . σ R ) — положительно определенная диагональная матрица , элементами которой являются σ 1 ≥. ≥σ R ≥0 — сингулярные значения матрицы A , равные квадратным корням из собственных значений матрицы A t A —

Рис. 24 SVD разложение

Дополняя матрицы P R и Q R ортонормированными столбцами, а матрицу D R нулевыми значениями, можно сконструировать матрицы P ( I × J ), D ( J × J ) и Q ( J × J ) такие, что

2.12. Линейное пространство

Рассмотрим все возможные векторы размерности N . Это множество называется линейным пространством размерности N и обозначается R N . Так как в R N включены все возможные векторы, то любая линейная комбинация векторов из R N будет также принадлежать этому пространству.

2.13. Базис линейного пространства

Любой набор из N линейно независимых векторов называется базисом в пространстве R N . Простейший пример базиса — это набор векторов

в каждом из которых только один элемент равен 1, а остальные равны нулю. Тогда любой вектор x = ( x 1 , x 2 . x N ) t может быть представлен как линейная комбинация x = x 1 e 1 + x 2 e 2+ . + x N e N базисных векторов.

Базис, составленный из попарно ортогональных векторов, называется ортогональным , а если базисные вектора еще и нормированы, то этот базис называется ортонормированным .

2.14. Геометрическая интерпретация

Линейному пространству можно дать удобную геометрическую интерпретацию. Представим себе N -мерное пространство, в котором базисные вектора задают направления осей координат. Тогда произвольный вектор x = ( x 1 , x 2 . x N ) t можно изобразить точкой в этом пространстве с координатами ( x 1 , x 2 . x N ).

Рис. 25 Координатное пространство

2.15. Множественность базисов

В линейном пространстве могут быть неограниченное число базисов. Так, в пространстве R 3 помимо обычного ортонормированного базиса

можно установить и другой ортонормированный базис, например

Каждый базис можно представить матрицей B = ( b 1 . b N ), составленной из базисных векторов. Переход от одного базиса к другому осуществляется с помощью невырожденной квадратной матрицы T , т.е. B 2 = TB 1 .

2.16. Подпространство

Пусть имеется набор из K линейно независимых векторов x 1 , x 2 . x K в пространстве R N . Рассмотрим все возможные линейные комбинации этих векторов

x = α 1 x 1 + α 2 x 2 +. + α K x K

О получившимся множестве Q говорят, что оно является линейной оболочкой или что оно натянуто на векторы x 1 , x 2 . x K . По определению линейного пространства это множество Q само является линейным пространством размерности K . При этом оно принадлежит пространству R N , поэтому Q называется линейным подпространством R K в пространстве R N .

2.17. Проекция на подпространство

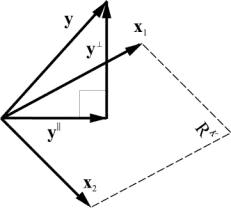
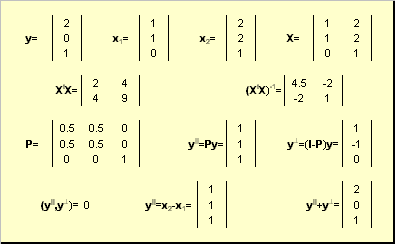
Рассмотрим подпространство R K , натянутое на векторы X = ( x 1 , x 2 . x K ) в пространстве R N . Матрица базиса X имеет размерность ( N × K ). Любой вектор y из R N может быть спроецирован на подпространство R K , т.е. представлен в виде

где вектор y || принадлежит R K , а вектор y ⊥ ортогонален y || .

Рис. 26 Проекция на подпространство

Проекцию y || можно представить как результат действия проекционной матрицы P

Проекционная матрица определяется как

Рис. 27 Проекционное разложение

Заключение

Матричные методы активно используются при анализе данных, в том числе и хемометрическими методами.

Знакомство с матрицами

Понятие и базовые операции.

Разработчики нейросетей говорят, что все нейросети — это просто бесконечное перемножение матриц. Мы решили разобраться, что это за матрицы и как их перемножать, а для этого пришлось полезть в линейную алгебру. И это оказалось не так сложно, как мы думали:

• Вектор — это просто группа из нескольких чисел, выстроенных в определённой последовательности. Например, рост и вес человека можно представить как вектор (172, 80). Ничего сложного.
• У вектора может быть внутри сколько угодно чисел. Главное — чтобы мы договорились, что для нас значат эти числа, и не меняли их местами просто так, произвольно.
• Векторы можно складывать, вычитать, умножать. Это чуть сложнее, чем с обычными числами.
• У вектора есть понятие линейной зависимости. Грубо говоря — параллельны друг другу векторы или нет. От этого зависит, какие операции можно делать с этими векторами.

Вектор — это «кирпичик» линейной алгебры. На его основе мы переходим к понятию матрицы.

Что такое матрица

Если вектор — это строка с числами в определённом порядке, то матрица — это таблица с числами в определённом порядке. Как у любой таблицы, у матрицы есть столбцы и строки. В них сидят какие-то числа. Всё вместе — это математический объект, то есть в каких-то случаях всю эту таблицу можно рассматривать как единое целое и совершать с ним операции.

Матрицы принято обозначать большими буквами латинского алфавита вроде А, В, С, D и так далее.

Числа внутри матрицы называют элементами. Каждый элемент обозначается двумя цифрами: первая цифра указывает на строку, а вторая — на столбец. Это адрес числа внутри матрицы. Например, элемент А₂₃ означает, что нужное число находится во второй строке и третьем столбце. Нумерация элементов нужна для записи формул и устного объяснения того, где находится нужное число в матрице.

В матрице может находиться неограниченное количество строк, столбцов и элементов. Из-за этого матрицы бывают разных видов и могут обладать разными особенностями. Например, если в матрице совпадает число строк и столбцов, то такая матрица называется квадратной.

В этой статье и в следующих материалах мы будем рассматривать разные виды матрицы и постепенно изучим их особенности.

Общая схема матрицы Пример квадратной матрицы с пятью строками и столбцами. Записывается как матрица размера 5×5. В числовой матрице мы не нумеруем элементы — они закрепляются за числами по умолчанию. Например, элементу А₂₃ соответствует число три

Простые операции с матрицами

Вынесение минуса за пределы матрицы. Если внутри матрицы у большинства элементов знак минус, то часто это мешает расчётам или приводит к ошибкам. Чтобы этого избежать, от минуса избавляются. Для этого нужно вынести минус за пределы матрицы и изменить знак всех элементов внутри самой матрицы.

И наоборот: если внутри матрицы у большинства элементов знак минус и перед матрицей стоит минус, то минус можно внести в матрицу.

Выносим минус за пределы матрицы и получаем вместо двадцати одного отрицательного элемента — четыре Перед матрицей минус, и внутри у большинства элементов минус. Вносим минус в матрицу и делаем её удобной для дальнейших вычислений

Умножение матрицы на число. Для умножения матрицы на число достаточно каждый элемент матрицы умножить на это число.

Пример умножения матрицы на число

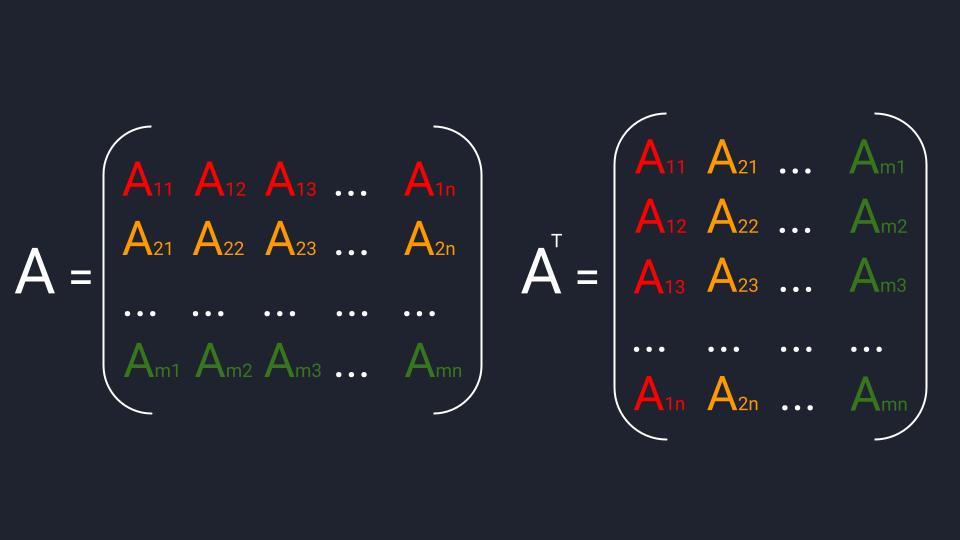
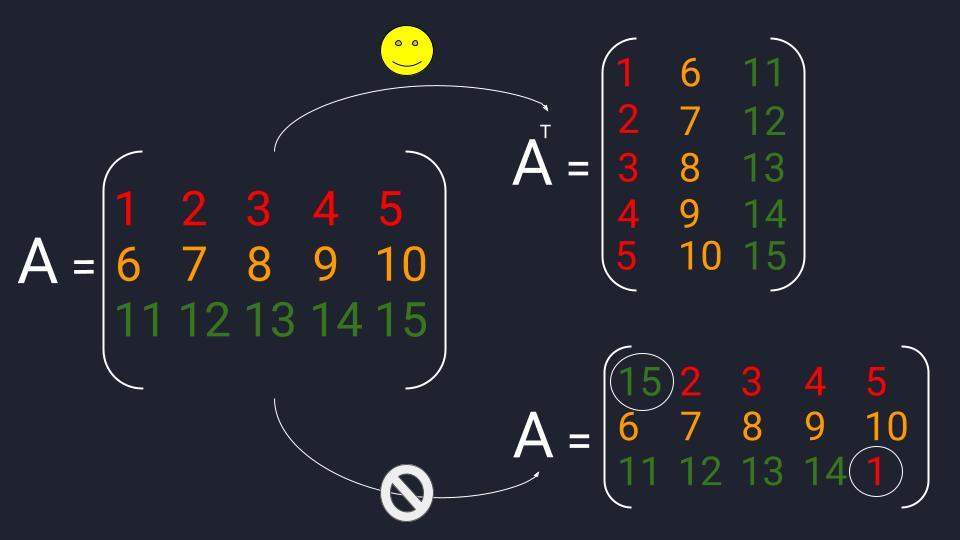
Транспонирование матрицы. Это операция, которая позже нам понадобится для решения матричных уравнений. Для транспонирования мы берём известную матрицу, меняем в ней местами строки со столбцами и получаем новую матрицу. Как бы поставили матрицу набок.

⚠️ При этом в матрице запрещено в произвольном порядке менять элементы. Зато можно полностью менять местами строки или столбцы. Если мы поменяем местами первую и вторую строку, то это останется прежняя матрица.

Схема транспонирования матриц: первая строка переходит в первый столбец, вторая строка — во второй столбец и так далее в зависимости от количества элементов матрицы Пример транспонирования. Транспонированная матрица обозначается буквой той же матрицы, из которой она получилась + надстрочечный индекс в виде печатной буквы «Т» Матрицу можно перетасовывать, но это нужно делать по правилам. Транспонирование — одно из таких правил

Сложение и вычитание матриц

Если в нескольких матрицах совпадает число строк и столбцов, то мы можем их складывать и вычитать. Для вычислений нам нужно поэлементно сложить или вычесть каждый элемент матриц: первый элемент первой матрицы складываем с первым элементом второй матрицы или вычитаем из него и так далее. В результате получаем новую матрицу.

Пример сложения двух прямоугольных матриц с тремя строками и двумя столбцами Пример вычитания двух матриц

Умножение матриц

Матрицы умножаются по принципу строка на столбец. Мы умножаем первую строку первой матрицы, на первый столбец второй матрицы, складываем результаты и получаем первый элемент новой матрицы. По аналогичной схеме вычисляем все остальные элементы. Звучит запутанно, поэтому идём по шагам:

1. У нас есть две матрицы A и B. Их нужно перемножить, чтобы получить новую матрицу C.
2. Размер матрицы A два на два: есть две строки и два столбца. Первая строка состоит из элементов А₁₁ и А₁₂; вторая — А₂₁ и А₂₂.
3. У матрицы B такая же размерность: есть две строки и два столбца. Первая строка состоит из элементов B₁₁ и B₁₂; вторая — B₂₁ и B₂₂.
4. У нас две одинаковые по размеру матрицы с двумя строками и столбцами. Это значит, что и матрица C будет размером два на два. Первая строка будет состоять из элементов C₁₁ и C₁₂; вторая — C₂₁ и C₂₂.
5. Считаем элемент C₁₁. Умножаем первый элемент первой строки матрицы А (А₁₁) на первый элемент первого столбика матрицы B (B₁₁). Это первая часть, после которой ставим знак плюс. Вторая часть: умножаем второй элемент первой строчки матрицы А (А₁₂) на второй элемент первого столбика матрицы B (B₂₁). Складываем обе части и получаем первый элемент первой строки матрицы С (C₁₁).
6. Считаем элемент C₁₂. Умножаем первый элемент первой строки матрицы А (А₁₁) на первый элемент второго столбика матрицы B (B₁₂). Это первая часть. Вторая часть: умножаем второй элемент первой строчки матрицы А (А₁₂) на второй элемент второго столбика матрицы B (B₂₂). Складываем части и получаем второй элемент первой строки матрицы С (C₁₂).
7. Считаем элемент C₂₁. Умножаем первый элемент второй строки матрицы А (А₂₁) на первый элемент первого столбика матрицы B (B₁₁). Это первая часть. Вторая часть: умножаем второй элемент второй строки матрицы А (А₂₂) на второй элемент первого столбика матрицы B (B₂₁). Складываем части и получаем первый элемент второй строки матрицы С (C₂₁).
8. Считаем элемент C₂₂. Умножаем первый элемент второй строки матрицы А (А₂₁) на первый элемент второго столбика матрицы B (B₁₂). Это первая часть. Вторая часть: умножаем второй элемент второй строки матрицы А (А₂₂) на второй элемент второго столбика матрицы B (B₂₂). Складываем части и получаем второй элемент второй строки матрицы С (C₂₂).

Если нам нужно найти матрицу в квадрате, то мы умножаем эту матрицу на саму себя. Если нужна матрица в кубе — умножаем её на саму себя три раза и так далее в зависимости от количества степеней. Если в одной из матриц все элементы нули, то она считается нулевой и после умножения на другую матрицу даёт нулевую матрицу — это как нуль умноженный на число всегда даёт нуль.

Формула умножения матриц Пример умножения квадратных матриц размерностью 2×2

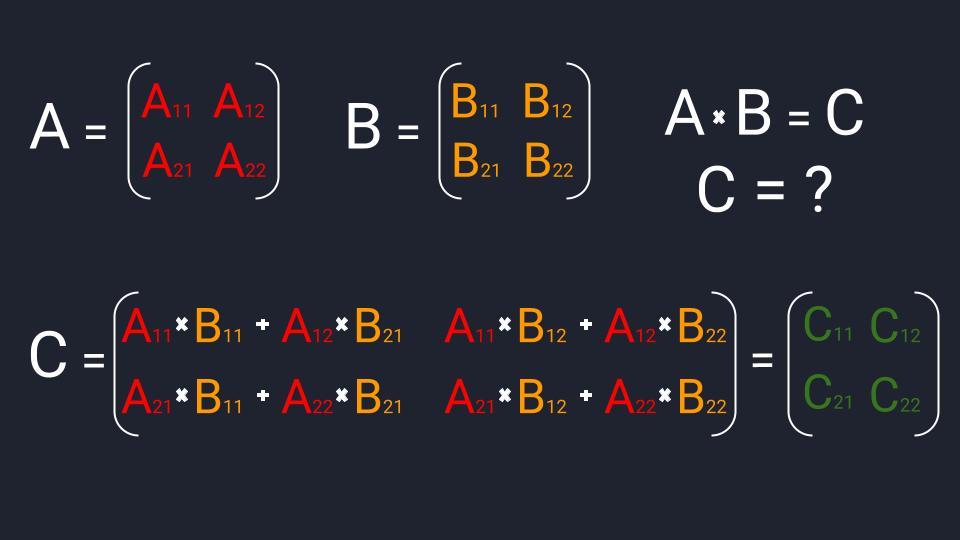
Что дальше

В следующий раз продолжим знакомиться с базовыми понятиями, которые нам понадобятся для решения матричных уравнений. А на сегодня Нео свободен 👽

Вектор и матрица 2022

Вектор против матрицы

Математика используется человеком в разных областях, которые его интересуют. Он используется в инженерных, естественных и социальных науках, медицине и других дисциплинах. Он использовался с тех пор, как человек обнаружил цифры и научился считать. Он был впервые использован человеком для записи времени, измерения земли, создания моделей для рисования и ткачества, а также в торговле. Египтяне и вавилоняне первыми использовали математику в области налогообложения, строительства и астрономии, а греки первыми изучали математику как науку. Математика имеет много полей, которые включают в себя геометрию и алгебру. Линейная алгебра, в частности, является ветвью математики, которая посвящена изучению векторных пространств и линейных операций, которые представлены матрицей или матрицами. Вектор определяется как математическая величина, имеющая величины и направления, такие как скорость. Он представлен буквой, которая также используется для представления действительного числа или скалярной величины. Чтобы отличить его от реального числа, он набирается жирным шрифтом со стрелкой над ним. Единичным вектором является вектор с величиной 1 и обозначается с карат (^) над переменной. Векторы используются в геометрии для упрощения трехмерных задач, а многие величины в физике являются векторными величинами. Вектор имеет возможность одновременно представлять величину и направление. Примером может служить ветер, который имеет скорость и направление, а также другие движущиеся объекты. С другой стороны, матрица представляет собой прямоугольный массив чисел, который является ключевым инструментом в линейной алгебре. Он используется для представления линейных преобразований и отслеживания коэффициентов в линейных уравнениях. Матрицы также используются в физике, теории графов, компьютерной графике, исчислении и сериализме. Элемент в матрице называется элементом или записью, и он представлен строчной буквой с двумя индексами индекса. Матрица представлена ​​буквой в верхнем регистре и обозначается скобками или скобками. Он может иметь строку (вектор строки) или столбец (вектор-столбец), который определяет компоненты векторов. Высшие размерные массивы чисел или матриц определяют компоненты обобщения вектора, который называется тензором.

1. Матрица представляет собой прямоугольную матрицу чисел, а вектор представляет собой математическую величину, имеющую величину и направление. 2. Вектор и матрица представляются буквой с вектором, начерченным полужирным шрифтом со стрелкой над ним, чтобы отличить его от вещественных чисел, а матрица набрана в прописной букве. 3. Векторы используются в геометрии для упрощения некоторых трехмерных задач, а матрицы — это ключевые инструменты, используемые в линейной алгебре. 4. Вектор — это массив чисел с одним индексом, а матрица — массив чисел с двумя индексами. 5. Когда вектор используется для представления величины и направления, матрица используется для представления линейных преобразований и отслеживания коэффициентов в линейных уравнениях.