Продолжения сторон ab и cd четырехугольника

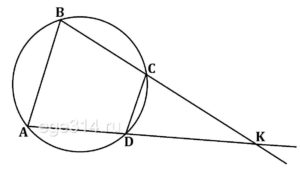
Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.

Поскольку четырёхугольник ABCD вписанный, сумма углов BAD и BCD равна 180°.

Получаем, что в треугольниках MBC и MDA углы MCB и MAD равны, угол M общий, следовательно, эти треугольники подобны.

Видео:№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать

Продолжения сторон AB и CD вписанного четырёхугольника ABCD пересекаются в точке P, а продолжения BC и AD — в точке Q. Докажите, что точки пересечения биссектрис углов AQB и BPC со сторонами четырёхугольника являются вершинами ромба.

Пусть P₁ и P₂ — точки пересечения биссектрисы угла BPC с окружностью, описанной около четырёхугольника ABCD, а Q₁ и Q₂ — биссектрисы угла AQB, причём точка P₁ лежит между P и P₂, Q₁ — между Q и Q₂. Тогда

AP₂ — BP₁ = DP₂ — CP₁, DQ₂ — AQ₁ = CQ₂ — BQ₁,

AP₂ + CP₁ = DP₂ + BP₁, AQ₁ + CQ₂ = DQ₂ + BQ₁.

Сложив почленно эти два равенства, получим, что

AP₂ + AQ₁ + CP₁ + CQ₂ = DP₂ + DQ₂ + BP₁ + BQ₁ = 180 o .

Если K — точка пересечения указанных биссектрис, то

PKQ = P₁KQ₁ = ( AP₂ + AQ₁ + CP₁ + CQ₂) = 90 o .

Если M и N — точки пересечения прямой Q₁Q₂ со сторонами AB и CD, то треугольник PMN — равнобедренный, т.к. его биссектриса PK является высотой. Поэтому MK = KN. Аналогично докажем, что K — середина второй диагонали полученного четырёхугольника. Следовательно, это ромб.

Видео:Геометрия Продолжение боковых сторон AB и CD в трапеции ABCD пересекаются в точке E. НайдитеСкачать

Решение №1222 Известно, что около четырехугольника АВСD можно описать окружность и что продолжения сторон АD и ВС …

Известно, что около четырехугольника АВСD можно описать окружность и что продолжения сторон АD и ВС четырёхугольника пересекаются в точке К. Докажите, что треугольники КАВ и КСD подобны.

Источник: ОГЭ Ященко 2021 (36 вар)

В ΔКАВ и ΔКСD ∠К общий.
Четырёхугольник АВСD вписан в окружность сумма противоположных углов равна 180°:

∠ABC + ∠ADC = 180º
∠ABC = 180º – ∠ADC

∠ADC и ∠СDK смежные их сумма равна 180º:

∠ADC + ∠СDK = 180º
∠СDK = 180º – ∠ADC

Из этих двух равенств получаем:

∠ABC = ∠СDK

Тогда ΔКАВ и ΔКСD подобны по двум равным углам.
Что и требовалось доказать.

🔍 Видео

Геометрия Продолжение боковых сторон AB и CD трапеции ABCD пересекаются в точке M. Найдите AM, еслиСкачать

ОГЭ 24 КАК РЕШИТЬ ЗАДАЧУ НА ДОКАЗАТЕЛЬСТВО ЧЕТЫРЕХУГОЛЬНИК И ОКРУЖНОСТЬСкачать

ОГЭ. Геометрия. Из открытого банка заданий ОГЭ (ФИПИ). Медианы №1Скачать

Задание 3 ЕГЭ по математике. Урок 41Скачать

ОГЭ по математике. Задача 25-2Скачать

Геометрия Известно, что около четырехугольника ABCD можно описать окружность и что продолжениеСкачать

✓ Самая сложная задача в ОГЭ-2020 | Задание 26. Математика | Геометрия | Борис ТрушинСкачать

Геометрия Точка E — середина боковой стороны CD трапеции ABCD. На стороне AB взяли точку K, такСкачать

Геометрия Боковые стороны AB и CD трапеции ABCD равны соответственно 28 и 35, а основание BC равно 7Скачать

Прямая Гаусса с доказательствомСкачать

✓ Олимпиадная задача по планиметрии за две минуты | #вызов | Борис ТрушинСкачать

2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать

Геометрия На продолжении стороны AB треугольника ABC за точку B отметили точку D Найдите радиусСкачать

Геометрия На стороне AB треугольника ABC отметили точку K а на продолжении стороны BC за точку CСкачать

Подобие || ОГЭ по математике №24Скачать

ОГЭ по математике, задание 26, тренировочный вариант 1Скачать

Геометрия В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит черезСкачать

Точка E середина стороны AD параллелограмма ABCDСкачать