Поворот вектора на 45 градусов

Поворот — это движение фигуры в пространстве вокруг неподвижной точки, принадлежащей этому же пространству.

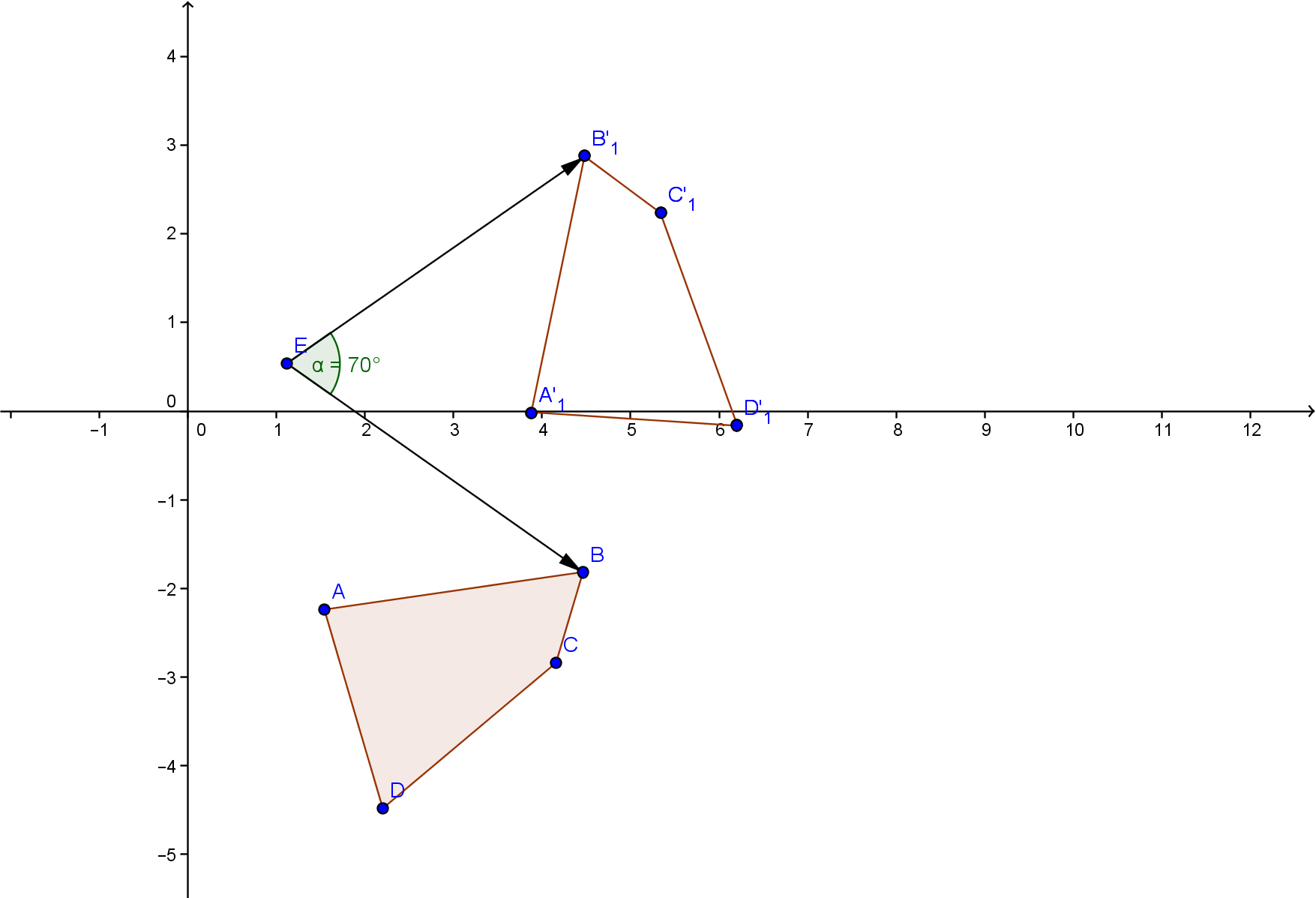
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Синтаксис

Координаты — строка, содержащая координаты в виде x:y (где x — абсцисса координаты, y — ордината координаты), разделенные хотя бы одним пробелом

Точка вращения — точка, относительно которой будет осуществляться поворот, всех заданных координат.

Поворот в градусах — поворот фигуры на заданный угол. Если число положительное — то поворот производится ПРОТИВ часовой стрелке, если отрицательный, то ПО часовой стрелке.

Видео:Угол между векторами. 9 класс.Скачать

Примеры

Пример: задан треугольник следующими координатами A(1:1) B (5:5) C(0:7)

Необходимо повернуть треугольник на 30 градусов против часовой стрелки относительно точки с координатами 3:3

Видео:Часть 3 Поворот вектораСкачать

О матрице поворота простыми словами

Когда Пифагор плыл по реке Хуанхэ, он увидел у берега, в лодке, задремавшего рыбака, в конической шляпе и с бамбуковой удочкой в руках.

Памятуя о том, что на Хабрахабр заглядывают люди разной математической подготовки, — однако, в поле интересов которых вполне может попадать тема линейных преобразований, — в связи с её практической значимостью, — я попробую рассказать об этом максимально доступно.

Видео:Скалярное произведение векторов. 9 класс.Скачать

Продолжим историю

Треугольные очертания лодки, шляпы и удочки над водой настолько поразили философа-математика, что он застыл как заворожённый.

Удочка рыбака аккуратно зависла над гладью вод Жёлтой Реки под углом, равным 45 градусам.

Лёгкий туман стелился над водой… и вдруг — поклёв. Рыбак потянул удочку, и она стала быстро набирать высоту, длина лески (катет А) стала расти на глазах, а расстояние от рыбака до самой лески стало уменьшаться (катет B). И самое интересное — длина самой удочки совсем не изменилась — телескопических удочек ещё не было, — даже когда она описала в воздухе дугу и оказалась почти над головой рыбака, под углом 90 градусов. Длина лески сравнялась с длиной удочки — катушки тогда уже были, — а расстояние между рыбаком и леской изменилось до 0, леска оказалась в руках рыбака.

Последний момент очень важен для понимания того, что происходит при умножении вектора-удочки на матрицу поворота.

Ностальгируем и думаем дальше.

Вспомним теорему Пифагора: квадрат длины удочки равен сумме квадратов катетов — самой лески и расстоянию между рыбаком и тем местом, где леска погружена в воду — С^2=А в квадрате + B в квадрате.

Представим, что длина удочки 4.2, длина (или высота над водой) лески 3, расстояние между рыбаком и местом, где леска погружена в воду тоже 3.

Видео:Матрица поворотаСкачать

Окунёмся в поиски

1) найдём то, как соотносится между собой длина лески с длиной удочки — синус угла а.
2) найдём то, как соотносится длина отрезка между рыбаком и местом погружения лески с длиной удочки — косинус а. Считаем:

А теперь порассуждаем
Что будет если катет А разделить на sin(a)?! т.е.:

Получаем длину удочки — гипотенузу.
А если мы умножим катет А на sin(а)?!

Отметим это расстояние на гипотенузе — 2.1.

На оставшееся расстояние также приходится — 2.1, так как очевидно:

Это означает, то как в текущий момент времени синус и косинус делят гипотенузу. Поскольку квадрат гипотенузы это 4.2*4.2, то вопрос: что будет если 4.2 умножить на 2.1?! На ту самую её часть, с которой связан один из катетов:

Тоже самое для второго катета.

Нашли катеты. И убедились в том, что со времён Пифагора ничего не изменилось.

Видео:Геометрия 9 класс (Урок№30 - Поворот.)Скачать

Далее

Теперь ещё раз осуществим умножение катета А на sin(a), катета B на cos(a).

Снова получили число равное длине удочки… и мы вплотную подобрались к матрице поворота.

Напомню формулу

Возьмём её нижнюю часть — получение точки y:

И сравним с вычислениями выше:

Как две капли воды. Y в нашем случае окажется равным 4.2.
Если применить первую часть формулы к вычислениям, то получим:

Иными словами случится так:

x станет 0 — рыбак поймает леску.
y станет 4.2 — леска сравняется с длиной удочки.

Помним, что для вычисления x синус и косинус меняются местами.

Ф в данном случае равно 45 градусам (Ф = 0.7 ) и при таком угле синус и косинус равны, что удобно для примера. В остальных случаях очевидно величины для синуса и косинуса будут другие. Например, для 40 градусов: cosdegree(40) = 0,7660444431, sindegree(40) = 0,6427876097 (если вы не согласны, обращайтесь в Яндекс, я пользовался его калькулятором).

Видео:§35 Формулы поворота координатных осейСкачать

В итоге

Применяя формулу к новым значениям x,y несколько раз — в цикле, наглядно увидим движение по окружности, каждый раз на 45 градусов.

Если требуется сдвинуть вектор-удочку на один градус, то его и подставляем в формулу на место Ф.

Как происходит вычисление тригонометрических функций?!
Как известно, для вычисления косинуса и синуса угла обычно используются готовые функции. Согласно информации по ссылке вычисление и точность зависят от системы. Для unix-систем есть по крайней мере два варианта: функция, написанная в недрах компании IBM и встроенная инструкция fsin на Ассемблере. Есть также библиотека fdlibm с достаточно наглядным кодом и комментариями, по которым видно, что синус и косинус вычисляются в этой библиотеке через число pi.

Видео:10 класс, 45 урок, Разложение вектора по трем некомпланарным векторамСкачать

А вдруг автор этой статьи все придумал?

Если немного изменить матрицу, то можно получить вращение по спирали или сделать из точки маятник.

Видео:4. Угловые повороты (повороты 90 градусов). Площадка. Делаем легко!Скачать

Матрицы поворота, углы Эйлера и кватернионы (Rotation matrices, Euler angles and quaternions)

Объект обычно определяется в удобной для его описания локальной системе координат (ЛСК), а его положение в пространстве — в глобальной системе координат (ГСК).

В трёхмерном пространстве переход из одной СК в другую описывается в общем случае системой линейных уравнений:

Уравнения могут быть записаны через матрицы аффинных преобразований в однородных координатах одним из 2-х способов:

В ортогональных СК оси X, Y и Z взаимно перпендикулярны и расположены по правилу правой руки:

На рисунке справа большой палец определяет направление оси, остальные пальцы — положительное направление вращения относительно этой оси.

Все три вектора направлений есть единичными.

Ниже приводится единичная матрица для 2-х способов записи уравнений геометрических преобразований. Такая матрица не описывает ни перемещения, ни вращения. Оси ЛСК и ГСК совпадают.

Далее рассматривается матрица для второго способа матричной записи уравнений (матрица справа). Этот способ встречается в статьях значительно чаще.

При использовании матрицы вы можете игнорировать нижнюю строку. В ней всегда хранятся одни и те же значения 0, 0, 0, 1. Она добавлена для того, чтобы мы могли перемножать матрицы (напомню правило перемножения матриц и отмечу, что всегда можно перемножать квадратные матрицы). Подробнее см. Композиция матриц. Однородные координаты.

Остальные 12 значений определяют координатную систему. Первый столбец описывает компоненты направления оси X(1,0,0). Второй столбец задает направление оси Y(0,1,0), третий – оси Z (0,0,1). Последний столбец определяет положение начала системы координат (0,0,0).

Как будет выглядеть матрица Евклидового преобразования (преобразование движения) для задания ЛСК , с началом в точке (10,5,0) и повёрнутой на 45° вокруг оси Z глобальной СК, показано на рисунке.

Рассмотрим сначала ось X. Если новая система координат повернута на 45° вокруг оси z, значит и ось x повернута относительно базовой оси X на 45° в положительном направлении отсчета углов. Таким образом, ось X направлена вдоль вектора (1, 1, 0), но поскольку вектор системы координат должен быть единичным, то результат должен выглядеть так (0.707, 0.707, 0). Соответственно, ось Y имеет отрицательную компоненту по X и положительную по Y и будет выглядеть следующим образом (-0.707, 0.707, 0). Ось Z направления не меняет (0, 0, 1). Наконец, в четвертом столбце вписываются координаты точки начала системы координат (10, 5, 0).

Частным случаем матриц геометрических преобразований есть матрицы поворота ЛСК относительно базовых осей ГСК. Вектора осей ЛСК здесь выражены через синусы и косинусы углов вращения относительно оси, перпендикулярной к плоскости вращения.

От матрицы преобразований размером 4*4 можно перейти непосредственно к матрице поворота 3*3, убрав нижний ряд и правый столбец. При этом, система линейных уравнений записывается без свободных элементов (лямда, мю, ню), которые определяют перемещение вдоль осей координат.

Путем перемножения базовых матриц можно получать комбинированные вращения. Ниже рассмотрены возможности комбинировать вращениями через матрицы поворота на примерах работы с углами Эйлера.

Видео:9 класс, 17 урок, Угол между векторамиСкачать

Матрицы поворота и углы Эйлера

От выбора осей и последовательности вращения зависит конечный результат. На рисунках отображена следующая последовательность вращения относительно осей ЛСК:

• оси Z (угол alpha);
• оси X (угол beta);
• оси Z (угол gamma).

Получил от читателя этой статьи вопрос: «Как понять, из каких углов поворота вокруг осей X,Y,Z можно получить текущее положение объекта, когда в качестве задания мы уже имеем повернутый объект, а нужно вывести его в это положение, последовательно повернув его из какого-то начального положения до полного совмещения с заданным?»

Мой ответ: «Если я правильно понял вопрос, то Вас интересует, как от начального положения перейти к заданному положению объекта, используя для этого элементарные базовые аффинные преобразования.

Начну с аналогии. Это как в шахматах. Мы знаем как ходит конь. Необходимо переместить его в результате многоходовки в нужную клетку на доске — при условии, что это возможно.

Подробно эта проблематика рассмотрена в статье Преобразование координат при калибровке роботов.

Умение правильно выбирать последовательность элементарных геометрических преобразований помогает в решении множества других задач (см. Примеры геометрических преобразований).»

Можно получить результирующую матрицу, которая определяет положение ГСК относительно ЛСК. Для этого необходимо перемножить матрицы с отрицательными углами в последовательности выполнения поворотов:

Почему знак угла поворота меняется на противоположный? Объяснение этому простое. Движение относительно. Абстрагируемся и представим, что ГСК меняет положение относительно неподвижной ЛСК. При этом направление вращения меняется на противоположное.

Перемножение матриц даст следующий результат:

Результирующую матрицу можно использовать для пересчета координат из ГСК в ЛСК:

Для пересчета координат из ЛСК в ГСК используется результирующая обратная матрица.

В обратной матрице последовательность поворота и знаки углов меняются на противоположные (в рассматриваемом примере снова на положительные) по сравнению с матрицей определения положения ГСК относительно ЛСК.

Перемножение матриц даст следующий результат:

Выше был рассмотрен случай определения углов Эйлера через вращение относительно осей ЛСК. То же взаимное положение СК можно получить, выполняя вращение относительно осей ГСК:

• оси z (угол (gamma+pi/2));
• оси y (угол угол beta);
• оси z (угол (-alpha)).

Определение углов Эйлера через вращение относительно осей ГСК позволяет также просто получить зависимости для пересчета координат из ЛСК в ГСК через перемножение матриц поворота.

В рамках рассматриваемой задачи вместо угла gamma в матрицe Az используем угол gamma+pi/2.

Также легко можно перейти к зависимостям для пересчета координат из ГСК в ЛСК.

Обратная матрица получается перемножением обратных матриц в обратном порядке по сравнению с прямым преобразованием. При этом каждая из обратных матриц вращения может быть получена заменой знака угла на противоположный.

Детально с теоретическими основами аффинных преобразований (включая и вращение) можно ознакомиться в статье Геометрические преобразования в графических приложениях

Примеры преобразований рассмотрены в статьях:

Видео:Видеоурок "Преобразование координат"Скачать

Axis Angle представление вращения

Выбрав подходящую ось (англ. rotation axis) и угол (англ. rotation angle) можно задать любую ориентацию объекта.

Обычно хранят ось вращения в виде единичного вектора и угол поворота вокруг этой оси в радианах или градусах.

q = [ x, y, z, w ] = [ v, w ]

В некоторых случаях удобно хранить угол вращения и ось в одном векторе. Направление вектора при этом совпадает с направлением оси вращения, а его длина равна углу поворота:

q = [ x, y, z]; w=sqrt (x*x +y*y +z*z)

В физике, таким образом хранят угловую скорость. Направление вектора совпадает с направлением оси вращения, а длина вектора равна скорости (в радианах в секунду).

Можно описать рассмотренные выше углы Эйлера через Axis Angle представление в 3 этапа:

q1 = [ 0, 0, 1, alpha]; q2 = [ 1, 0, 0, beta]; q3 = [ 0, 0, 1, gamma ]

Здесь каждое вращение выполняется относительно осей текущего положения ЛСК. Такое преобразование равнозначно рассмотренному выше преобразованию через матрицы поворота:

Возникает вопрос, а можно ли 3 этапа Axis Angle представления объединить в одно, подобно матрицам поворота? Попробуем решить геометрическую задачу по определению координат последнего вектора вращения в последовательности преобразований через Axis Angle представления:

q = [ x, y, z, gamma ]

Есть ли представление q= [x, y, z, gamma] композицией последовательности из 3-х этапов преобразований? Нет! Координаты x, y, z определяют всего лишь положение оси Z ЛСК после первого и второго этапов преобразований:

При этом ось Z, отнюдь, не есть вектор вращения для Axis Angle представления, которое могло бы заменить рассмотренные 3-х этапа преобразований.

Еще раз сформулирую задачу, которая математически пока не решена: «Необходимо найти значение угла (rotation angle) и положение оси (rotation axis), вращением относительно которой на этот угол можно заменить комбинацию из 3-х поворотов Эйлера вокруг осей координат».

К сожалению, никакие операции (типа объединения нескольких преобразований в одно) с Axis Angle представлениями нельзя выполнить. Не будем расстраиваться. Это можно сделать через кватернионы, которые также определяют вращение через параметры оси и угол.

Видео:9 класс, 18 урок, Скалярное произведение векторовСкачать

Кватернионы

Кватернион (как это и видно по названию) представляет собой набор из четырёх параметров, которые определяют вектор и угол вращения вокруг этого вектора. По сути такое определение ничем не отличается от Axis Angle представления вращения. Отличия лишь в способе представления. Как же хранят вращение в кватернионе?

q = [ V*sin(alpha/2), cos(alpha/2) ]

В кватернионе параметры единичного вектора умножается на синус половины угла поворота. Четвертый компонент — косинус половины угла поворота.

Таблица с примерами значений кватернионов:

Представление вращения кватернионом кажется необычным по сравнению с Axis Angle представлением. Почему параметры вектора умножаются на синус половины угла вращения, четвертый параметр — косинус половины угла вращения, а не просто угол?

Откуда получено такое необычное представление кватерниона детально можно ознакомиться в статье Доступно о кватернионах и их преимуществах. Хотя программисту не обязательно знать эти детали, точно также как и знать, каким образом получены матрицы преобразования пространства. Достаточно лишь знать основные операции с кватернионами, их смысл и правила применения.

Видео:Упражнение гараж автошкола. Заезд в бокс. Как правильно делать гараж. Бокс.Скачать

Основные операции над кватернионами

Кватернион удобно рассматривать как 4d вектор, и некоторые операции с ним выполняются как над векторами.

Видео:Парковка задним ходом. Способ 45º.Скачать

Сложение, вычитание и умножение на скаляр.

Смысл операции сложения можно описать как «смесь» вращений, т.е. мы получим вращение, которое находится между q и q’.

Что-то подобное сложению кватернионов выполнялось при неудачной попытке объединить 3 этапа Axis Angle представления.

Умножение на скаляр на вращении не отражается. Кватернион, умноженный на скаляр, представляет то же самое вращение, кроме случая умножения на 0. При умножении на 0 мы получим «неопределенное» вращение.

Пример сложения 2-х кватернионов:

Видео:Функции поворота на нужный угол. Самый удобный докер для Corel Draw от ДеревяшкинаСкачать

Норма и модуль

Следует различать (а путают их часто) эти две операции:

Модуль (magnitude), или как иногда говорят «длина» кватерниона:

Через модуль кватернион можно нормализовать. Нормализация кватерниона — это приведение к длине = 1 (так же как и в векторах):

Видео:Кватернионы | Вращение в 3D [Самая суть]Скачать

Обратный кватернион или сопряжение ( conjugate )

Обратный кватернион задает вращение, обратное данному. Чтобы получить обратный кватернион достаточно развернуть вектор оси в другую сторону и при необходимости нормализовать кватернион.

Например, если разворот вокруг оси Y на 90 градусов = (w=0,707; x = 0; y = 0,707; z=0), то обратный = (w=0,707; x = 0; y = -0,707; z=0).

Казалось бы, можно инвертировать только компоненту W, но при поворотах на 180 кватернион представляется как (w=1; x = 0; y = 0; z=0), то есть, у него длина вектора оси = 0.

Фрагмент программной реализации:

Видео:Как заехать в гараж с поворотом на 90градусов!Экзаменационное упражнение ГИБДД 2023г.Скачать

Инверсный (inverse) кватернион

Существует такой кватернион, при умножении на который произведение дает нулевое вращение и соответствующее тождественному кватерниону (identity quaternion), и определяется как:

Видео:Учимся вписываться в повороты. Практические примеры.Скачать

Тождественный кватернион

Записывается как q[0, 0, 0, 1]. Он описывает нулевой поворот (по аналогии с единичной матрицей), и не изменяет другой кватернион при умножении.

Видео:ЗАВАЛИЛ ГАРАЖ? | Что делать, если не попал в гараж на экзамене?Скачать

Скалярное произведение

Скалярное произведение полезно тем, что дает косинус половины угла между двумя кватернионами, умноженный на их длину. Соответственно, скалярное произведение двух единичных кватернионов даст косинус половины угла между двумя ориентациями. Угол между кватернионами — это угол поворота из q в q’ (по кратчайшей дуге).

Видео:А.7.18 Вот: это поворот!!! (+ДЗ)Скачать

Вращение 3d вектора

Вращение 3d вектора v кватернионом q определяется как

причем вектор конвертируется в кватернион как

и кватернион обратно в вектор как

Умножение кватернионов

Одна из самых полезных операций, она аналогична умножению двух матриц поворота. Итоговый кватернион представляет собой комбинацию вращений — сначала объект повернули на q, а затем на q’ (если смотреть из глобальной системы координат).

Примеры векторного и скалярного перемножения 2-х векторов векторное произведение — вектор: Скалярное произведение — число:

Пример умножения 2-х кватернионов:

Конвертирование между кватернионом и Axis Angle представлением

В разделе Axis Angle представление вращения была сделана неудачная попытка объединить 3 Axis Angle представления в одно . Это можно сделать опосредовано. Сначала Axis Angle представления конвертируются в кватернионы, затем кватернионы перемножаются и результат конвертируется в Axis Angle представление.

Пример конвертирования произведения 2-х кватернионов в Axis Angle представление:

Фрагмент программы на C:

Конвертирование кватерниона в матрицу поворота

Матрица поворота выражается через компоненты кватерниона следующим способом:

где

Проверим формулы конвертирования на примере конвертирования произведения 2-х кватернионов в матрицу поворотов:

Определяем элемент матрицы m[0][0] через параметры кватерниона:

Соответствующее произведению кватернионов (q1 и q2) произведение матриц поворотов было получено ранее (см. Матрицы поворота и углы Эйлера):

Как видим, результат m[0][0], полученный через конвертирование, совпал с значением в матрице поворота.

Фрагмент программного кода на С для конвертирования кватерниона в матрицу поворота:

При конвертировании используется только умножения и сложения, что является несомненным преимуществом на современных процессорах.

Часто для задания вращений используют только кватернионы единичной длины, но это не обязательно и иногда даже не эффективно. Разница между конвертированием единичного и неединичного кватернионов составляет около 6-ти умножений и 3-х сложений, зато избавит во многих случаях от необходимости нормировать (приводить длину к 1) кватернион. Если кусок кода критичен по скорости и вы пользуетесь только кватернионами единичной длины тогда можно воспользоваться фактом что норма его равна 1.

Конвертирование матрицы поворота в кватернион

Конвертирование матрицы в кватернион выполняется не менее эффективно, чем кватерниона в матрицу, но в итоге мы получим кватернион неединичной длины. Его можно нормализовать.

Фрагмент программного кода конвертирования матрицы поворота в кватернион: