2018-05-31 
По прямому проводнику круглого сечения течет ток $I$. Найти поток вектора Пойнтинга через боковую поверхность участка данного проводника, имеющего сопротивление $R$.
Предположим, что радиус проводника равен $R_$. Тогда плотность тока проводимости равна
где $rho = frac$ — удельное сопротивление.
Внутри проводника имеется магнитное поле, определяемое формулой
$H cdot 2 pi R_ = I$ или $H = frac <2 pi R_>$ на краю
Энергия, протекающий в секунду в сечении длины $l$
Таким образом, энергия, протекающая в проводнике $= I^ R$.
Видео:Билет №38 "Поток энергии"Скачать

5.7. Активное и внутреннее индуктивное сопротивление проводов
Активное и внутреннее индуктивное сопротивление проводников можно определить с помощью теоремы Умова – Пойнтинга в комплексной форме.
Перед тем, как записать теорему Умова – Пойнтинга 4.8) в комплексной форме, рассмотрим вопрос о полной мощности в цепи синусоидального тока. Полная мощность
Здесь 

Пусть цепь синусоидального тока содержит последовательно соединенные активные сопротивления R, индуктивность L и емкость С.
Тогда реактивная мощность
Здесь 

Таким образом, реактивная мощность Q равна разности между магнитной WМ и электрической WЭ энергиями цепи, умноженной на 2w.
Введем также в рассмотрение комплексный вектор Пойнтинга
Последнее выражение отличается от мгновенного значения вектора Пойнтинга тем, что здесь комплексная величина вектора напряженности 

С учетом этого, теорему Умова – Пойнтинга (4.8) можно переписать в следующем виде:
Первое слагаемое правой части данного выражения представляет собой активную мощность, второе – реактивную. Таким образом, теорему Умова – Пойнтинга можно записать еще следующим образом:
В таком виде ее и используют для определения активного и внутреннего индуктивного сопротивления проводников на переменном токе. С этой целью подсчитывают поток вектора Пойнтинга через боковую поверхность проводника на необходимой длине (например, 1 м) и делят его на квадрат тока, протекающего по проводнику, в результате чего и получают комплексное сопротивление проводника на этой длине
В качестве примера определим активное и внутреннее индуктивное сопротивление цилиндрического провода (см. рис. 5.11) на длине l:
Здесь d – радиус ( новое обозначение введено, чтобы отличать от сопротивления) проводника; 

а также выражения (5.11), (5.12) и (5.13), преобразуем уравнение (5.14) к следующему виду:
Если рассчитать сопротивление данного провода на длине l постоянному току, то оно будет равно 1.273?10 -3 l. Таким образом,
Отсюда видно, что активное сопротивление провода почти в четыре раза превышает сопротивление провода постоянному току.
Отметим, что если поле обладает цилиндрической симметрией, как в случае прямолинейного одиночного провода (обратный провод находится достаточно далеко) или в случае прямолинейного цилиндрического кабеля, то выражение для определения активного и внутреннего индуктивного сопротивления провода можно получить и иным путем

Здесь 
Формула (5.15) просто получается и из выражения (5.14), если в нем заменить квадрат тока его значением, определенным с помощью закона полного тока
Видео:Поток векторного поля через замкнутую поверхностьСкачать

Теорема и вектор Пойнтинга в стационарном электромагнитном поле
Теорема Пойнтинга основана на законе сохранения энергии и является важнейшей интегральной теоремой электричества и магнетизма, используемой в инженерной практике при разработке и проектировании большинства энергоемких электротехнических устройств, включая сложные системы генерирования, транспортировки и потребления электроэнергии, в особенности — нетрадиционных энергосистем с минимально возможным внутренним потреблением энергии.
Исходя из методологических соображений, обратимся вначале к простейшему наглядному примеру. На рис. 1.3 изображен замкнутый контур с током I, включающий в себя источник энергии (например, в виде источника ЭДС Е и сопротивления г,,), сопротивление Двнеш и соединительные провода с сечением Snp.
Источник генерирует энергию, которая потребляется элементами цепи:
Во всем пространстве выделим далее объем V, содержащий источник ЭДС Е, внутреннее сопротивление rv и соединительные провода. Этот объем на рис. 1.3 ограничен замкнутой поверхностью S3aMKH, которая рассекает соединительные провода Snp и разделяет внутреннюю и внешнюю части пространства:
Очевидным при этом является то, что часть энергии, развиваемой источником, сосредоточена во внутреннем объеме V (I 2 rv), а оставшаяся часть покидает объем V или излучается из объема V через замкнутую поверхность S3aMKH (Ризл) и расходуется во внешнем сопротивлении Рвнеш.
Таким образом, исходное уравнение баланса мощности (1.95) может быть представлено в виде
где Ризл носит название мощности излучения.
Покажем, что законы и уравнения электричества и магнетизма позволяют в самом общем виде получить математическое описание всех составляющих баланса мощности (1.97).
Для этого выделим в пространстве объем V (рис. 1.4), в котором существуют электрическое поле (5, 5^, Е и обусловленное им магнитное поле (Я).
Объем V обладает проводимостью у и ограничен замкнутой поверхностью S3aMKH.
Стационарное электромагнитное поле в объеме описывается уравнениями

Если (1.98) умножить скалярно на Е, а (1.99) — на Н и из (1.98) вычесть (1.99), получим:
а после соответствующего преобразования левой части (1.100):
Интегрируя далее левую и правую части (1.101) по объему V и используя известную теорему Остроградского — Гаусса
получим следующее уравнение:
Общее уравнение баланса мощности (1.103) и называют теоремой Пойнтинга, а новый вектор
равный векторному произведению векторов Е и Н, называют вектором Пойнтинга.
Сопоставляя исходное уравнение баланса мощности (1.97) с полученным уравнением (1.103), находим:
Таким образом, вектор Пойнтинга (1.104) имеет размерность поверхностной плотности мощности (ВА/м 2 ), а мощность излучения (1.107), покидающая объем V, определяется как поток вектора Пойнтинга через замкнутую поверхность, ограничивающую этот объем.
При отсутствии сторонних источников теорема Пойнтинга (1.103) упрощается и принимает вид
а если объем V представляется в виде проводника с током I и сопротивлением R, то
и, следовательно, сопротивление проводника может вычисляться при помощи выражения:
которое является прямым следствием теоремы Пойнтинга.
Энергетическое представление сопротивления проводника (1.110) по сравнению с традиционной формулой Ома
является более общим, а при сложной конфигурации проводника и неоднородных граничных условиях — единственно возможным.
Простейший пример такого проводника сложной конфигурации, выполненного из листового материала толщиной Д, приведен на рис. 1.5.
Если в этом листе рассчитать поле тока (б, Е) и определить интегральное значение выделенной мощности
то лист в целом можно характеризовать энергетическим понятием
и при известном суммарном токе I в листе определить некоторое эквивалентное напряжение
Теорема Пойнтинга позволяет также определить роль пространства, окружающего проводник, в передаче электрической энергии.
Обратимся вновь к исходному примеру. Если замкнутой поверхностью S3aMKH охватить внешнее сопротивление Квнеш (рис. 1.6), то в соответствии с теоремой Пойнтига мощность, выделяемая в этом сопротивлении, должна быть равна взятому с обратным знаком потоку вектора Пойнтинга через эту замкнутую поверхность:
Как и в исходном примере, замкнутая поверхность S3aMKH не является однородной, а состоит из поверхности внешней среды SBHeui и поперечных сечений проводов Snp. Следовательно, (1.112) можно представить в виде
Из выражения (1.113) следует, что мощность (или энергия) принципиально может поступать в объем V с сопротивлением 1?внеш по двум различным каналам — электрическим проводам и непроводящему окружающему пространству.
Общую сравнительную количественную оценку этим двум потокам энергии можно дать с помощью следующего конкретного примера. Цилиндрический провод радиуса а (рис. 1.7) обтекается током I, удельная проводимость провода равна у. Требуется определить поток вектора Пойнтинга через замкнутую поверхность, охватывающую провод на длине I.
Очевидно, что эта замкнутая поверхность будет состоять из двух торцевых и боковой поверхности:
Для решения поставленной задачи вначале нужно рассчитать Е(а), Н(а), П(а) на боковой поверхности провода и Е(г), Н(г), П(г) внутри него, на торцевых поверхностях, а затем найти соответствующие составляющие потоков и суммарный поток вектора Пойнтинга П через всю замкнутую поверхность. Рассмотрим произвольную_то_чку внутри провода и определим направления векторов Е, Н, П. Исходя из условий осевой симметрии Н = На.
Поскольку 8 = уЕ, электрическая напряженность Е направлена вдоль оси провода. Очевидно, что вектор П лежит в плоскости поперечного сечения провода, а это значит, что его поток через торцевые сечения равен нулю. Но если это так, то мощность в объем провода поступает только из окружающего пространства через боковую поверхность провода и расходуется там на тепло. Таким образом, поскольку
В окружающем пространстве магнитная напряженность в силу осевой симметрии будет изменяться так же, как в поле линейного провода с током I:
На поверхности провода
На боковой поверхности вектор dS направлен в сторону внешней нормали, а вектор П — вглубь провода. Поэтому на боковой поверхности
причем на всей боковой поверхности П(а) = const. В итоге
Этот пример говорит о том, что направление вектора Пойн- тинга одновременно указывает и на направление передачи потока энергии, а его величина определяет интенсивность этого потока или поверхностную плотность мощности излучения.
🔥 Видео
Урок 222. Поток вектора напряженности электрического поляСкачать

Вектор Умова-Пойнтинга ● 3Скачать

Вектор Умова-Пойнтинга ● 1Скачать

Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Вектор Умова-Пойнтинга ● 2Скачать

Вектор Умова-Пойнтинга ● 5Скачать

Вектор Пойнтинга и энергия конденсатораСкачать

Теорема Умова-Пойнтинга, вектор Пойнтинга. Переменное электрическое поле. Пару слов об экзамене.Скачать

Урок 225. Задачи на поток вектора напряженности электрического поляСкачать

5 Вектор ПойтингаСкачать

Поток векторного поля через поверхность. Поверхностный интеграл.Скачать
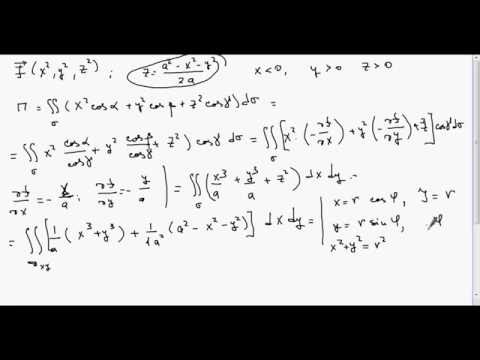
Вектор Пойнтинга и энергия. ЭНПСкачать

Электричество - Семинар 6 - Задача 3 - Иродов 3.350Скачать

Урок 224. Напряженность поля неточечных зарядовСкачать

Поток вектора магнитной индукцииСкачать

Билет №31 "Ток смещения"Скачать

Найти поток векторного поля через замкнутую поверхность S (нормаль внешняя).Скачать

Оптика - Лекция 1Скачать







































