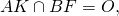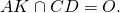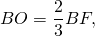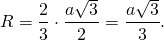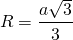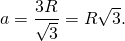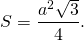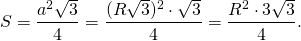В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.
Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Определение равностороннего треугольника
Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.
Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.
Видео:№122. Прямая CD перпендикулярна к плоскости правильного треугольника ABC. Через центр О этогоСкачать
Свойства равностороннего треугольника
Свойство 1
В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.
Свойство 2
В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.
CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.
Свойство 3
В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.
Свойство 4
Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.
Свойство 5
Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.
- R – радиус описанной окружности;
- r – радиус вписанной окружности;
- R = 2r.
Свойство 6
В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:
1. Высоту/медиану/биссектрису:
2. Радиус вписанной окружности:
3. Радиус описанной окружности:
4. Периметр:
5. Площадь:
Видео:№204. Прямая ОМ перпендикулярна к плоскости правильного треугольника ABC и проходит через центр ОСкачать
Пример задачи
Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.
Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:
Видео:Центр тяжести треугольникаСкачать

Окружность, описанная около правильного треугольника
Окружность, описанная около правильного треугольника, обладает всеми свойствами описанной около произвольного треугольника окружности и, кроме того, имеет свои собственные свойства.
1) Центр описанной около треугольника окружности — точка пересечения серединных перпендикуляров к его сторонам.
Поскольку в равностороннем треугольнике медианы, высоты и биссектрисы совпадают, центр описанной около правильного треугольника окружности лежит в точке пересечения его медиан, высот и биссектрис.
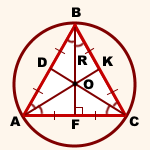
точка O — центр описанной окружности.
AK, BF и CD — медианы, высоты и биссектрисы треугольника ABC.
2) Расстояние от центра описанной окружности до вершин треугольника равно радиусу. Так как центр описанной около равностороннего треугольника окружности лежит на пересечении его медиан, а медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то радиус описанной окружности составляет две трети от длины медианы:
Таким образом, формула радиуса описанной около правильного треугольника окружности —
И обратно, сторона равностороннего треугольника через радиус описанной окружности —
3) Формула для нахождения площади правильного треугольника по его стороне —
Отсюда можем найти площадь через радиус описанной окружности:
Таким образом, формула площади площади правильного треугольника через радиус описанной окружности —
4) Центр описанной около правильного треугольника окружности совпадает с центром вписанной в него окружности.
5) Радиус описанной около равностороннего треугольника окружности в два раза больше радиуса вписанной окружности:
Видео:Геометрия - Построение правильного треугольникаСкачать

Центр треугольника
Треугольник — наиболее распространенная форма деталей в сферах машиностроения и строительства. Точка пересечения 3-х медиан считается центром треугольника. На эту точку приходится также центр тяжести и центр симметрии предметов треугольной формы. При разработке дизайнерских, инженерных проектов очень важно точно рассчитать центр тяжести элементов металлической или бетонной конструкции.
Существует несколько понятий центра для треугольника.
Инцентр — точка пересечения его биссектрис. Это — центр описанной около треугольника окружности.
Ортоцентр — точка пересечения его высот.
Центр тяжести,центр масс или центроид (обозн. М) — точка пересечения медиан треугольника.
Рассмотрим треугольник. Определим середины его сторон и соединим их с противолежащими углами. Точка пересечения медиан и будет центром тяжести тр-ка. Медиана делится этой точкой в пропорции 2:1 , (считая от вершины тр-ка).
Видео:№143. Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4 смСкачать
Как найти центр треугольника
Если известны координаты его вершин, найдем сумму трех значений координат «х» и трех значений координат «у». Поделим каждую сумму на 3, получим среднее значение сумм координат «х» и «у», что и будет координатами центра тяжести.
Центром равностороннего треугольника является точка пересечения высот, биссектрис и медиан.
Центр равностороннего треугольника является также центром вписанной и описанной окружности.
Центроид расположен на отрезке, соединяющем ортоцентр и центр описанной окружности. Центроид делит отрезок 2:1.
Быстро найти центр треугольника G можно с помощью онлайн калькулятора. Для этого:
- ввести в поле калькулятора координаты вершин треугольника;
- нажать кнопку Вычислить. Калькулятор вычислит значение центра треугольника G.
🌟 Видео
Формулы равностороннего треугольника #shortsСкачать

Площадь треугольника. Как найти площадь треугольника?Скачать

По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Геометрия Через центр O правильного треугольника ABC проведена прямая DO перпендикулярная плоскостиСкачать

Найти центр кругаСкачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать

КАК НАЙТИ ДЛИНУ ОКРУЖНОСТИ, ОПИСАННОЙ ОКОЛО ПРАВИЛЬНОГО ТРЕУГОЛЬНИКА? Примеры | ГЕОМЕТРИЯ 9 классСкачать

Построение равностронего треугольника.Скачать

У равностороннего треугольника есть центр симметрии. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Задание 15 ОГЭ. Медиана равностороннего треугольникаСкачать

НАЙДИТЕ ВЫСОТУ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКАСкачать

Площадь равностороннего треугольникаСкачать

Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать