Поток вектора магнитной индукции через некоторый (5 видео)

Поток вектора магнитной индукции через некоторый

Поток вектора магнитной индукции через некоторый проводящий контур изменяется от 50 мкВб до 20 мкВб. Сопротивление контура 15 Ом. Найдите модуль электрического заряда, который при этом протекает через контур. Ответ дайте в мкКл.

При изменении магнитного потока в контуре возникает ЭДС индукции

Под действием этой ЭДС возникает ток, равный, согласно закону Ома для полной цепи,

С другой стороны, сила тока есть отношение заряда, прошедшего за единицу времени

Объединяя все уравнения, получим выражения для электрического заряда в контуре

Содержание

Поток вектора магнитной индукции (магнитный поток)
Определение
Связь магнитного потока и работы сил магнитного поля
Теорема Гаусса для магнитного поля
Поток вектора магнитной индукции
Формула магнитного потока
В чем измеряется магнитный поток
Связь магнитного потока и работы сил магнитного поля
Теорема Гаусса для магнитного поля
💡 Видео

Видео:Поток вектора магнитной индукцииСкачать

Поток вектора магнитной индукции (магнитный поток)

Вы будете перенаправлены на Автор24

Видео:Поток вектора магнитной индукции через некоторый проводящий контур изменяется от 10 мкВб до - №26998Скачать

Определение

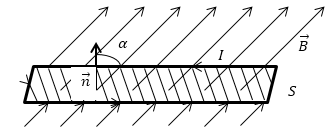
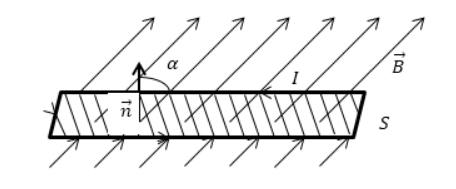
Потоком вектора магнитной индукции (магнитным потоком) (Ф) через площадку S называют скалярную величину равную:

где $alpha $ угол между $overrightarrow$ и $overrightarrow$, $overrightarrow$ — нормаль к площадке S.

Ф равен количеству линий магнитной индукции, которые пересекают площадку S (рис.1). Поток магнитной индукции может быть положительным и отрицательным. Знак потока зависит от выбора положительного направлении нормали к площадке S. Обычно, положительное направление нормали связывают с направлением обхода контура током. За положительное направление нормали принимают поступательное перемещение правого винта, при вращении его по току.

В том случае, если магнитное поле неоднородно, S не является плоской, то поверхность можно разбить на элементарные площадки dS, которые рассматриваются как плоские, а поле на этой площадке можно считать однородным. В таком случае магнитный поток (dФ) можно через такую поверхность определить как:

Тогда полный поток через поверхность S находится как:

Основная единица измерения магнитного потока в системе СИ — вебер (Вб). $1 Вб=frac$.

Видео:Урок 281. Электромагнитная индукция. Магнитный поток. Правило ЛенцаСкачать

Связь магнитного потока и работы сил магнитного поля

Элементарную работу ($delta A$), которую совершают силы магнитного поля можно выразить через элементарное изменение потока вектора магнитной индукции (dФ):

[delta A=IdФ left(4right).]

В том случае, когда проводник с током совершил конечное перемещение, а сила тока постоянна, то работа сил поля равна:

где $Ф_1$ — поток через контур в начале перемещения, $Ф_2$ — поток через контур в конце перемещения.

Видео:ПОТОК ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ для ЕГЭ по физике // SATTAROVFAMILYСкачать

Теорема Гаусса для магнитного поля

Суммарный магнитный поток через замкнутую поверхность S равен нулю:

Уравнение (6) справедливо для любых магнитных полей. Это уравнение аналог теоремы Остроградского — Гаусса в электростатике (в вакууме):

Уравнение (6) означает, что источником магнитного поля являются не магнитные заряды (их в природе не существует), а электрические токи. Данную теорему мы подробно рассматривали в разделе «Отсутствие в природе магнитных зарядов».

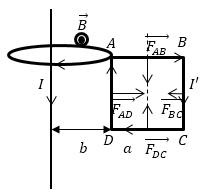
Задание: Недалеко от бесконечно длинного прямого проводника с током I находится квадратная рамка, по которой течет ток с силой $I’$. Сторона рамки равна $а$. Рамка лежит в плоскости с проводом (рис.2). Расстояние от ближайшей стороны рамки до проводника равно b. Найдите работу магнитной силы при удалении рамки из поля. Считать токи постоянными.

Индукция магнитного поля длинного проводника с током в части, где расположена квадратная рамка, направлена на нас.

При решении этой задачи необходимо помнить, что рамка с током находится в неоднородном поле, магнитная индукция убывает при удалении от провода.

В качестве основы для решения задачи используем формулу связи потока и работы:

$I’$- сила тока в рамке, $Ф_1$- поток через квадратную рамку, когда расстояние от ее стороны, ближайшей к проводу равна $b$. $Ф_2=0$, так как в конечном положении рамка вне магнитного поля по условию. Следовательно, формула (1.1) запишется как:

Выберем направление нормали ($overrightarrow$) к квадратному контуру от нас (по правилу правого винта). Тогда для всех элементов поверхности, которая ограничена контуром квадратной рамки угол между нормалью $overrightarrow$ и вектором $overrightarrow$ равен $pi $. Тогда формула для потока через поверхность рамки на расстоянии x от провода имеет вид:

где индукция магнитного поля бесконечно длинного проводника с током силы I равна:

Следовательно, весь поток из (1.3) найдем как:

Подставим формулу (1.5) в выражение (1.2) найдем искомую работу:

Видео:Физика Поток вектора магнитной индукцииСкачать

Поток вектора магнитной индукции

Магнитный поток Φ через площадку S (поток вектора магнитной индукции) – это скалярная величина:

Φ = B S cos α = B n S = B → S → с углом между n → и B → , обозначаемым α , n → является нормалью к площадке S .

Видео:Индукция магнитного поля | Физика 9 класс #37 | ИнфоурокСкачать

Формула магнитного потока

Φ равняется количеству линий магнитной индукции, пересекающих площадку S , как показано на рисунке 1 . Поток магнитной индукции по формуле принимает положительные и отрицательные значения. Его знак зависит от выбора положительного направления нормали к площадке S . Зачастую положительное направление нормали связано с направлением обхода контура током. За такое направление берут поступательное перемещение правого винта во время его вращения по току.

Видео:Билет №27 "Магнитный поток. Взаимоиндукция"Скачать

В чем измеряется магнитный поток

В случае неоднородности магнитного поля S не будет плоской, а плоскость может быть разбита на элементарные площадки d S , рассматриваемые в качестве плоских, поле которых также считается однородным. Определение магнитного потока d Φ производится через эту поверхность. Запись примет вид:

d Φ = B d S cos α = B → d S → .

Нахождение полного потока через поверхность S :

Φ = ∫ S B d S cos α = ∫ S B → d S → .

Основной единицей измерения магнитного потока в системе СИ считаются веберы ( В б ) . 1 В б = 1 Т л 1 м 2 .

Видео:Электромагнитная индукция. ЕГЭ Физика. Николай НьютонСкачать

Связь магнитного потока и работы сил магнитного поля

Элементарная работа δ A , совершаемая силами магнитного поля, выражается через элементарное изменение потока вектора магнитной индукции d Φ :

Если проводник с током совершает конечное перемещение, сила тока постоянна, то работа сил поля равняется:

A = I Φ 2 — Φ 1 с Φ 1 , обозначаемым потоком через контур в начале перемещения, Φ 2 является потоком через контур в конце перемещения.

Видео:Билет №16 "Теорема о циркуляции и теорема Гаусса для магнитного поля"Скачать

Теорема Гаусса для магнитного поля

Значение суммарного магнитного потока через замкнутую поверхность S равняется нулю:

Выражение ∮ B → d S → = 0 является справедливым для любых магнитных полей. Данное уравнение считается аналогом теоремы Остроградского-Гаусса в электростатике в вакууме:

Запись ∮ B → d S → = 0 говорит о том, что источник магнитного поля – это не магнитные заряды, а электрические токи.

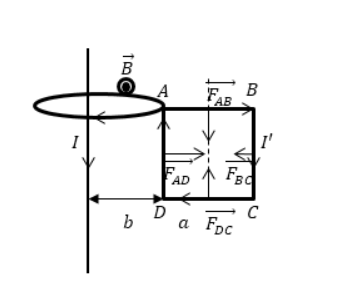
Дан бесконечно длинный прямой проводник с током I , недалеко от которого имеется квадратная рамка. По ней проходит ток с силой I ‘ . Сторона рамки равна a . Она располагается в одной плоскости с проводом, как показано на рисунке 2 . Значение расстояния от ближайшей стороны рамки до проводника равняется b . Найти работу магнитной силы при удалении рамки из поля. Считать токи постоянными.

Индукция магнитного поля длинного проводника с током в части, где расположена квадратная рамка, направляется на нас.

Следует учитывать нахождение рамки с током в неоднородном поле, что означает убывание магнитной индукции при удалении от провода.

За основу возьмем формулу магнитного потока и работы, которая их связывает:

A = I ‘ Φ 2 — Φ 1 ( 1 . 1 ) , где I ‘ принимают за силу тока в рамке, Φ 1 – за поток через квадратную рамку при расстоянии от ее стороны к проводу равняющимся b . Φ 2 = 0 . Это объясняется тем, что конечное положение рамки вне магнитного поля, как дано по условию. Отсюда следует, запись формулы ( 1 . 1 ) изменится:

A = — I ‘ Φ 1 ( 1 . 2 ) .

Перейдем к нормали n → и выберем ее направление к квадратному контуру относительно нас, используя правило правого винта. Отсюда следует, что для всех элементов поверхности, ограниченной при помощи контура квадратной рамки, угол между нормалью n → и вектором B → равняется π . Запись формулы потока через поверхность рамки на расстоянии х от провода примет вид:

d Φ = — B d S = — B · a · d x = — μ 0 2 π I l d x x ( 1 . 3 ) , значение индукции магнитного поля бесконечно длинного проводника с током силы I будет:

B = μ 0 2 π x I l ( 1 . 4 ) .

Отсюда следует, что для нахождения всего потока из ( 1 . 3 ) потребуется:

Φ 1 = ∫ S — μ 0 2 π I l d x x = — μ 0 2 π I l ∫ b b + a d x x = — μ 0 2 π I l · ln b + a b ( 1 . 5 ) .

Произведем подстановку формулы ( 1 . 5 ) в ( 1 . 2 ) . Искомая работа равняется:

A = I ‘ μ 0 2 π I l · ln b + a b .

Ответ: A = μ 0 2 π I I ‘ l · ln b + a b .

Найти силу, действующую на рамку, из предыдущего примера.

Для нахождения искомой силы, действующей на квадратную рамку с током в поле длинного провода, предположим, что под воздействием магнитной силы рамка смещается на незначительное расстояние d x . Это говорит о совершении силой работы, равной:

δ A = F d x ( 2 . 1 ) .

Элементарная работа δ A может быть выражена как:

δ A = I ‘ d Φ ( 2 . 2 ) .

Произведем то же с силой, применяя формулы ( 2 . 1 ) , ( 2 . 2 ) . Получаем:

F d x = I ‘ d Φ → F = I ‘ d Φ d x ( 2 . 3 ) .

Используем выражение, которое было получено в примере 1 :

d Φ = — μ 0 2 π I l d x x → d Φ d x = — μ 0 2 π I l x ( 2 . 4 ) .

Произведем подстановку d Φ d x в ( 2 . 3 ) . Имеем:

F = I ‘ μ 0 2 π I l x ( 2 . 5 ) .

Каждый элемент контура квадратной рамки находится под воздействием сил (силы Ампера). Отсюда следует, что на рамку действует 4 силы, причем на стороны A B и D C равные по модулю и противоположные по направлению. Выражение принимает вид:

F A B → + F D C → = 0 ( 2 . 6 ) , то есть их сумма равняется нулю. Тогда значение результирующей силы, приложенной к контуру, запишется:

F → = F A D → + F B C → ( 2 . 6 ) .

Используя правило левой руки, получаем направление этих сил вдоль одной прямой в противоположные стороны:

F = F A D — F B C ( 2 . 7 ) .

Произведем поиск силы F A D , действующей на сторону A D , применив формулу ( 2 . 5 ) , где x = b :

F A D = I ‘ м 0 2 π I l b ( 2 . 8 ) .

Значение F B C будет:

F B C = I ‘ μ 0 2 π I l b + a ( 2 . 9 ) .

Для нахождения искомой силы:

F = I ‘ μ 0 2 π I l b — I ‘ μ 0 2 π I l b + a = I I ‘ μ 0 l 2 π 1 b — 1 b + a .

Ответ: F = I I ‘ μ 0 l 2 π 1 b — 1 b + a . Магнитные силы выталкивают рамку с током до тех пор, пока она находится в первоначальной ориентации относительно поля провода.