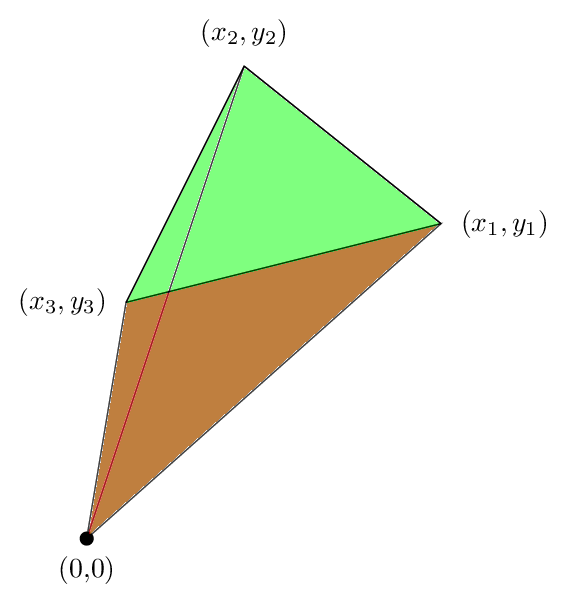Пересечение круга и треугольника (3 видео)

Треугольник вписанный в окружность

Содержание

Определение
Формулы
Радиус вписанной окружности в треугольник
Радиус описанной окружности около треугольника
Площадь треугольника
Периметр треугольника
Сторона треугольника
Средняя линия треугольника
Высота треугольника
Свойства
Доказательство
Вычислить площадь пересечения круга и треугольника?
11 ответов
как найти площадь многоугольника
площадь пересечения окружности с многоугольником
Как проверить принадлежность треугольника пересечению двух окружностей?
📹 Видео

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

Периметр треугольника вписанного в окружность,
если известны все стороны:

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

Средняя линия треугольника вписанного
в окружность, если известно основание:

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

Высота треугольника вписанного в окружность,
если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Свойства

Центр вписанной в треугольник окружности
находится на пересечении биссектрис.
В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну.
Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора.
Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров.
Все вершины треугольника, вписанного
в окружность, лежат на окружности.
Сумма всех углов треугольника — 180 градусов.
Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.

Видео:Построение равностронего треугольника.Скачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

Проведем серединные
перпендикуляры — HO, FO, EO.
O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника.
Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Видео:Линия пересечения плоскостейСкачать

Вычислить площадь пересечения круга и треугольника?

Как вычислить площадь пересечения треугольника (заданного как три (X,Y) пары) и окружности (X,Y,R)? Я провел некоторые поиски, но безрезультатно. Это для работы, а не для школы. 🙂

это будет выглядеть примерно так в C#:

Видео:Пересечение биссектрис треугольника в одной точке, Геометрия 7 классСкачать

11 ответов

Если вы хотите точное решение (или, по крайней мере, так точно, как вы можете получить с помощью арифметики с плавающей запятой), то это потребует много работы, потому что есть так много случаев для рассмотрения.

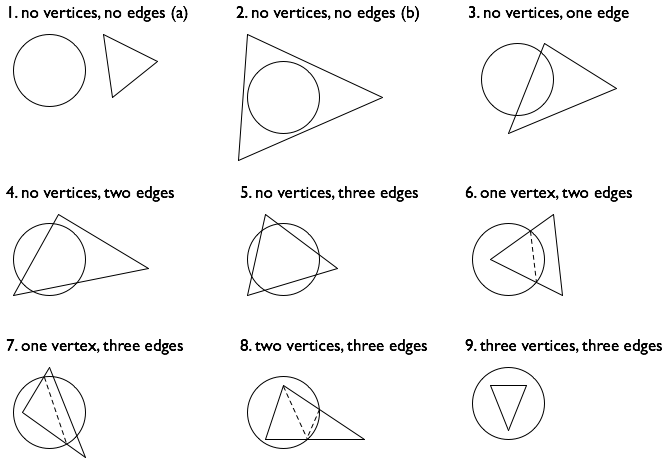
Я насчитал девять различных случаев (классифицированных на рисунке ниже по числу вершин треугольника внутри круга и числу ребер треугольника, которые пересекаются или содержатся в круге):

(однако, этот вид перечисление геометрических случаев хорошо известно, что это сложно, и меня совсем не удивило бы, если бы я пропустил один или два!)

определите для каждой вершины треугольника, находится ли она внутри круга. Полагаю, ты знаешь, как это сделать.

определите для каждого края треугольника, пересекает ли он окружность. (Я написал один метод здесь, или см. любую книгу вычислительной геометрии.) Вам необходимо вычислить точки пересечения (если таковые имеются) для использования на шаге 4.

определить, какие из девяти случаев у вас есть.

вычислить площадь пересечения. Случаи 1, 2 и 9 легко. В остальных шести случаях я нарисовал пунктирные линии, чтобы показать, как разбить область пересечения на треугольники и круговых сегментов на основе исходных вершин треугольника и точек пересечение, вычисленное на Шаге 2.

этот алгоритм будет довольно деликатным и склонным к ошибкам, которые влияют только на один из случаев, поэтому убедитесь, что у вас есть тестовые случаи, которые охватывают все девять случаев (и я предлагаю перестановку вершин тестовых треугольников). Обратите особое внимание на случаи, когда одна из вершин треугольника находится на краю круга.

Если вам не нужно точное решение, то растеризация фигур и подсчет пикселей в пересечении (как было предложено несколькими другими респондентами) кажется гораздо более простым подходом к коду и, соответственно, менее подверженным ошибкам.

сначала я напомню, как найти площадь многоугольника. Как только мы это сделаем, алгоритм поиска пересечения между многоугольником и кругом должен быть легко понятен.

Видео:Нахождение пересечения двух треугольниковСкачать

как найти площадь многоугольника

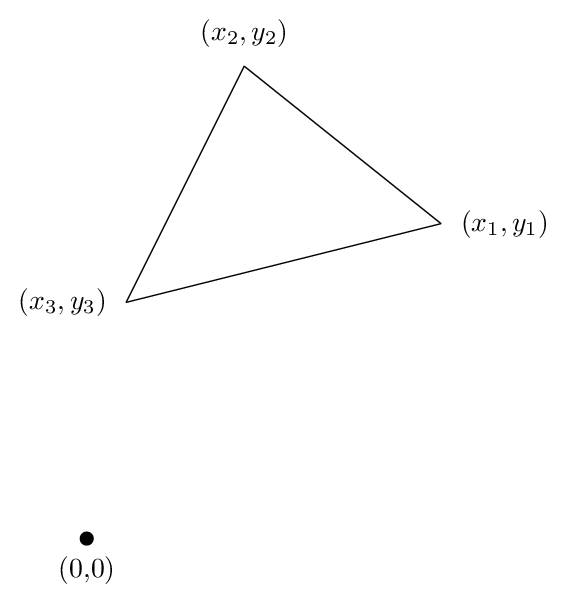
давайте посмотрим на случай треугольника, потому что там появляется вся существенная логика. Предположим, что у нас есть треугольник с вершинами (x1,y1), (x2,y2) и (x3, y3), когда вы идете вокруг треугольника против часовой стрелки, как показано в следующая цифра:

затем вы можете вычислить площадь по формуле

а=(Х1 У2 + У3 х2 + х3 У1 — x2y1 — Х3 У2 — x1y3)/2.

чтобы понять, почему эта формула работает, давайте переставим ее так, чтобы она была в виде

A=(x1 y2 — x2 y1)/2 + (x2 y3 — x3 y2)/2 + (x3 y1 — x1y3 )/2.

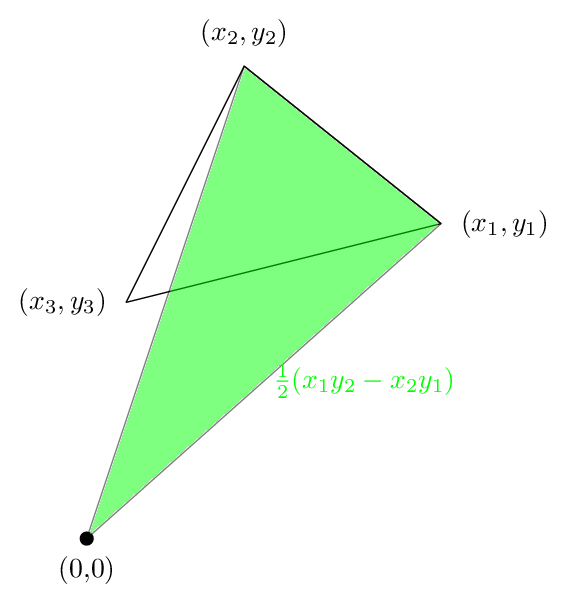
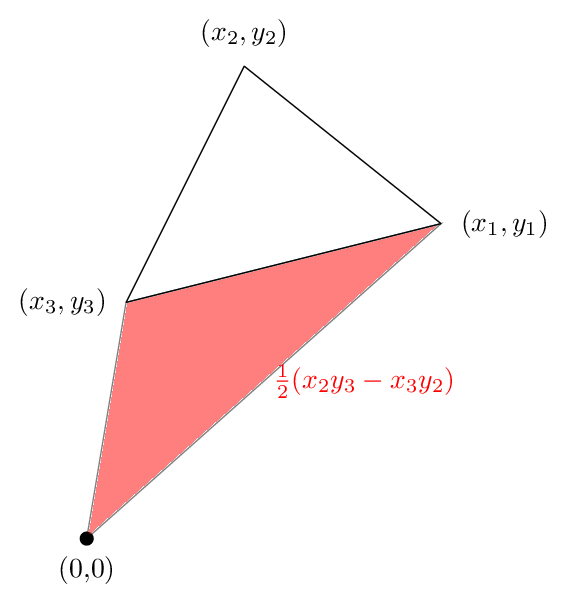
теперь первый термин-это следующая область, которая является положительной в нашем случае:

если не ясно, что площадь зеленого область действительно (x1 y2-x2 y1)/2, тогда прочитайте этой.

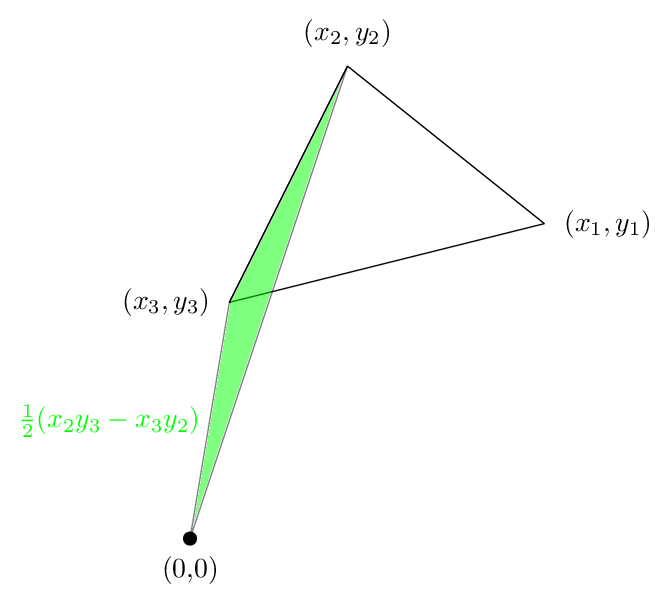
второй член-это область, которая снова положительна:

и третья область показана на следующем рисунке. На этот раз область отрицательная

добавив эти три мы получаем следующую картину

мы видим, что зеленая область, которая была вне треугольника, отменена на Красной площади, так что чистая площадь-это только площадь треугольника, и это показывает, почему наша формула была верна в этом случае.

то, что я сказал выше, было интуитивным объяснением того, почему формула области была правильной. Более строгим объяснением было бы наблюдать, что при вычислении площади от ребра площадь, которую мы получаем, является той же областью, которую мы получим от интегрирования r^2dθ / 2, поэтому мы эффективно интегрируем r^2dθ / 2 вокруг границы многоугольника и Стоксом теорема, это дает тот же результат, что и интегрирование rdrdθ над областью, ограниченной многоугольником. Поскольку интегрирование rdrdθ над областью, ограниченной многоугольником, дает область, мы заключаем, что наша процедура должна правильно дать область.

Видео:Центр кругаСкачать

площадь пересечения окружности с многоугольником

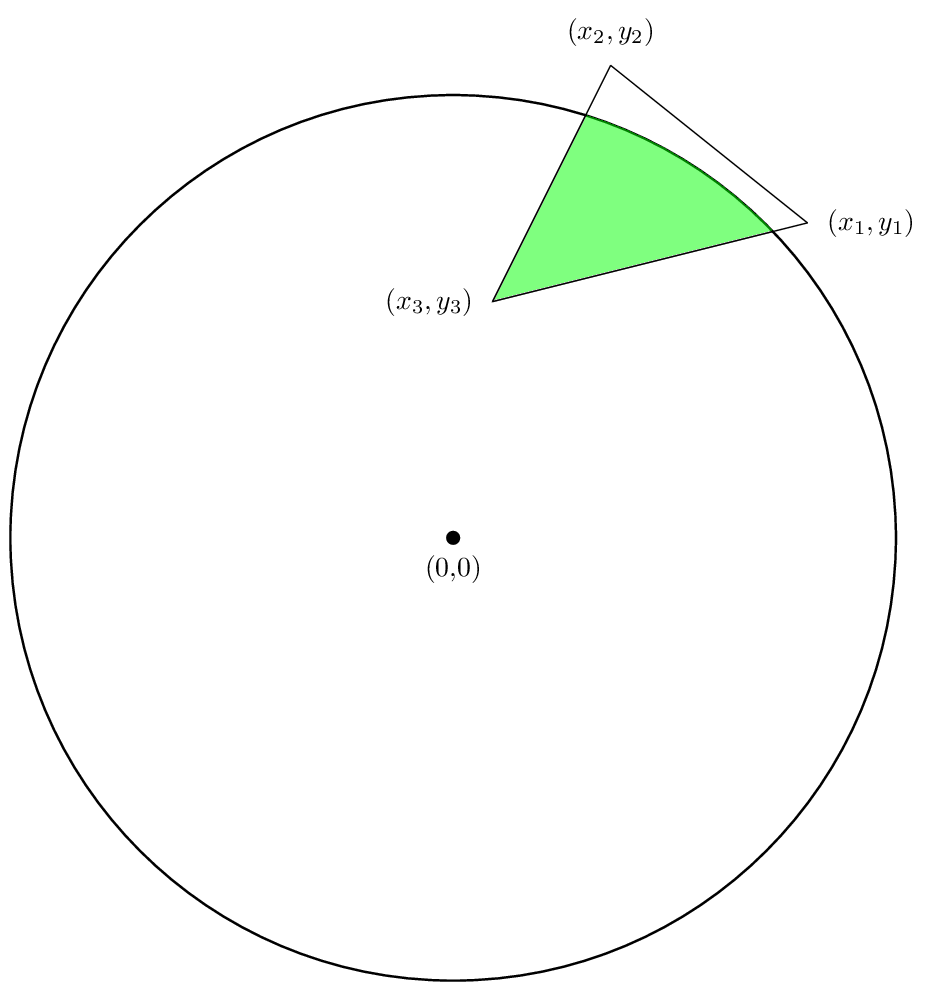
теперь давайте обсудим, как найти площадь пересечения круга радиуса R с многоугольником, как показано в следующем рисунок:

нас интересует найдите площадь зеленой области. Мы можем, как и в случае с одним многоугольником, разбить наш расчет на поиск области для каждой стороны многоугольника,а затем добавить эти области.

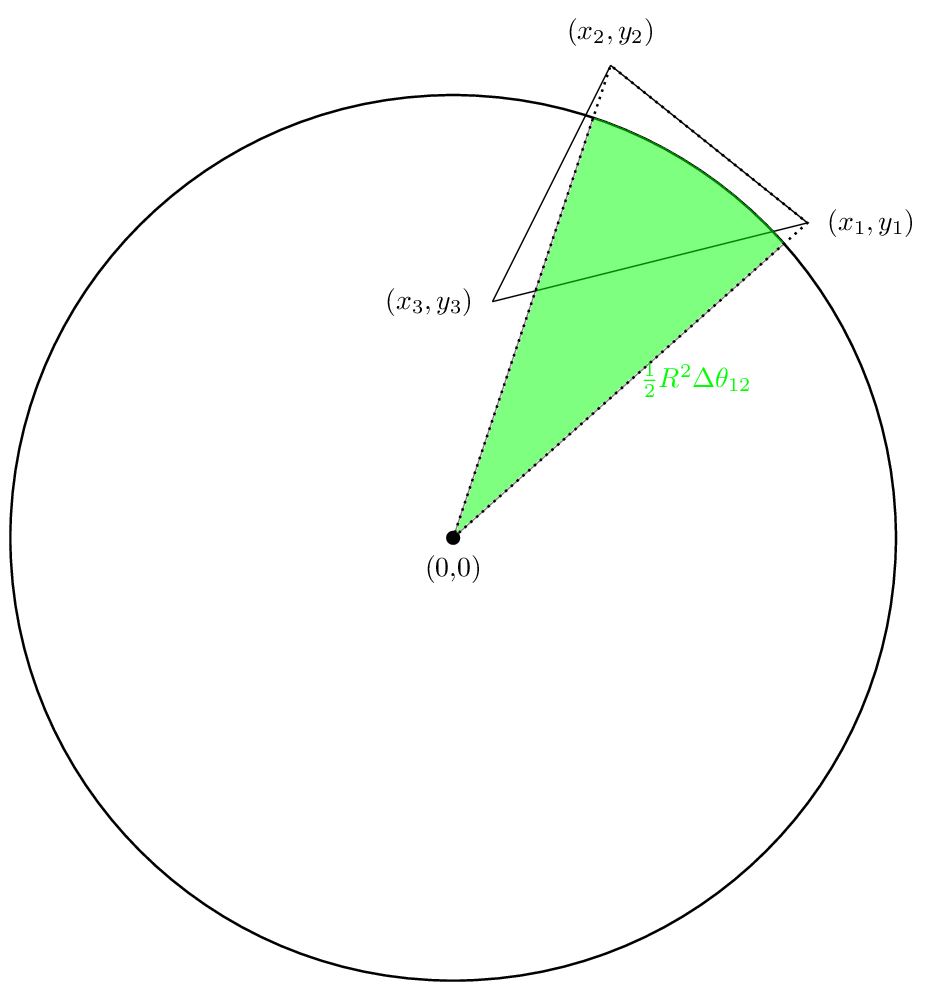
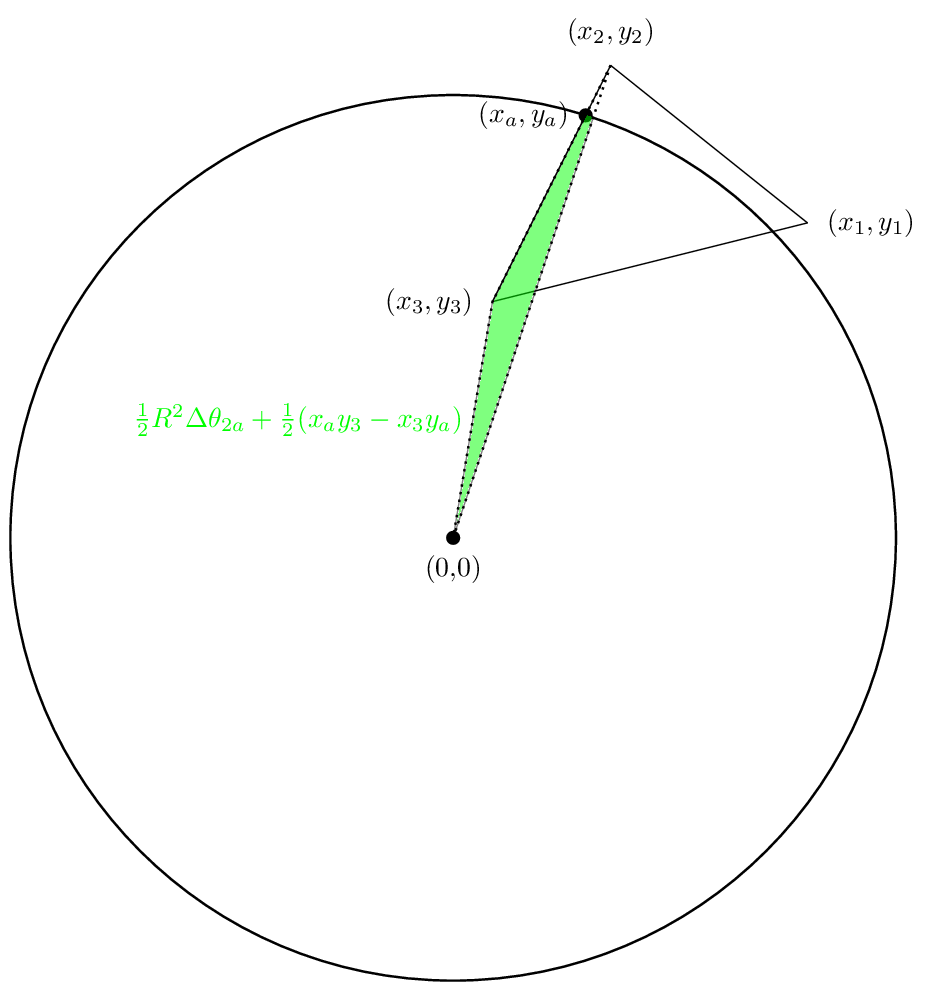
наша первая область будет выглядеть так:

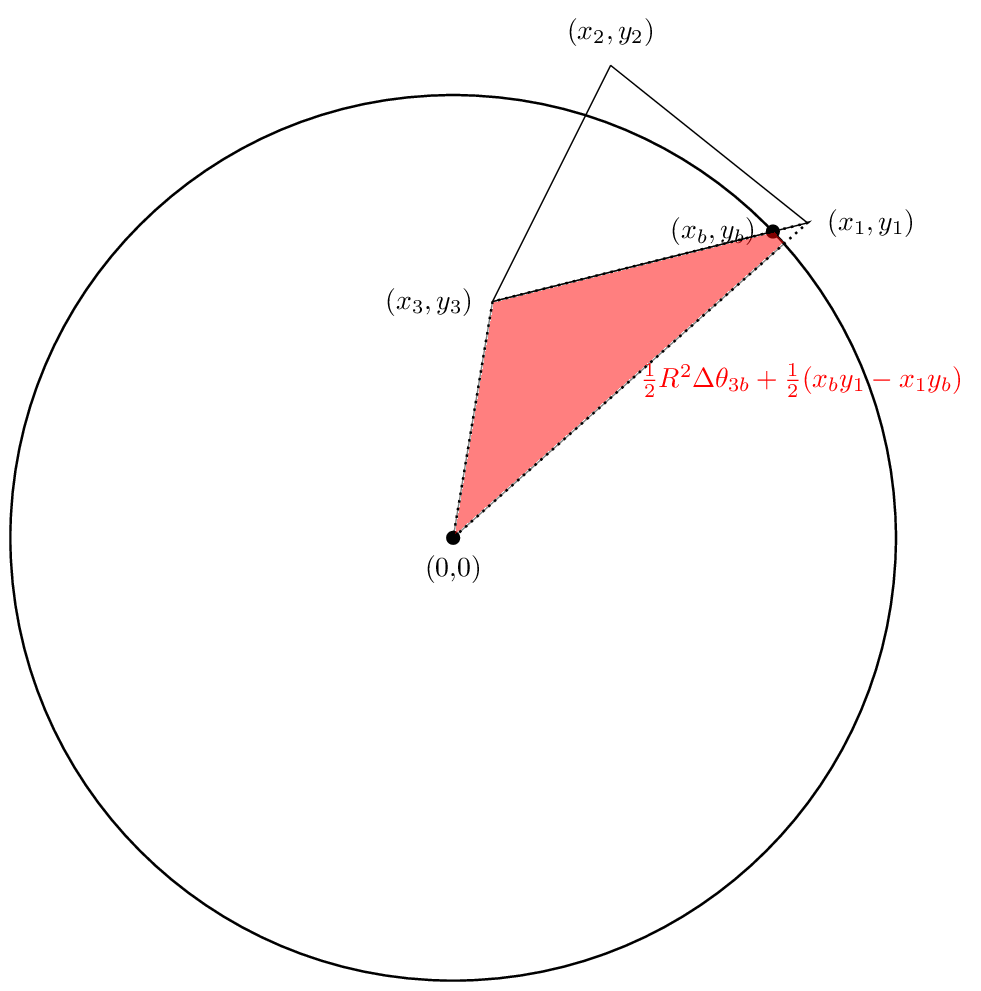
вторая область будет выглядеть так

и третья область будет

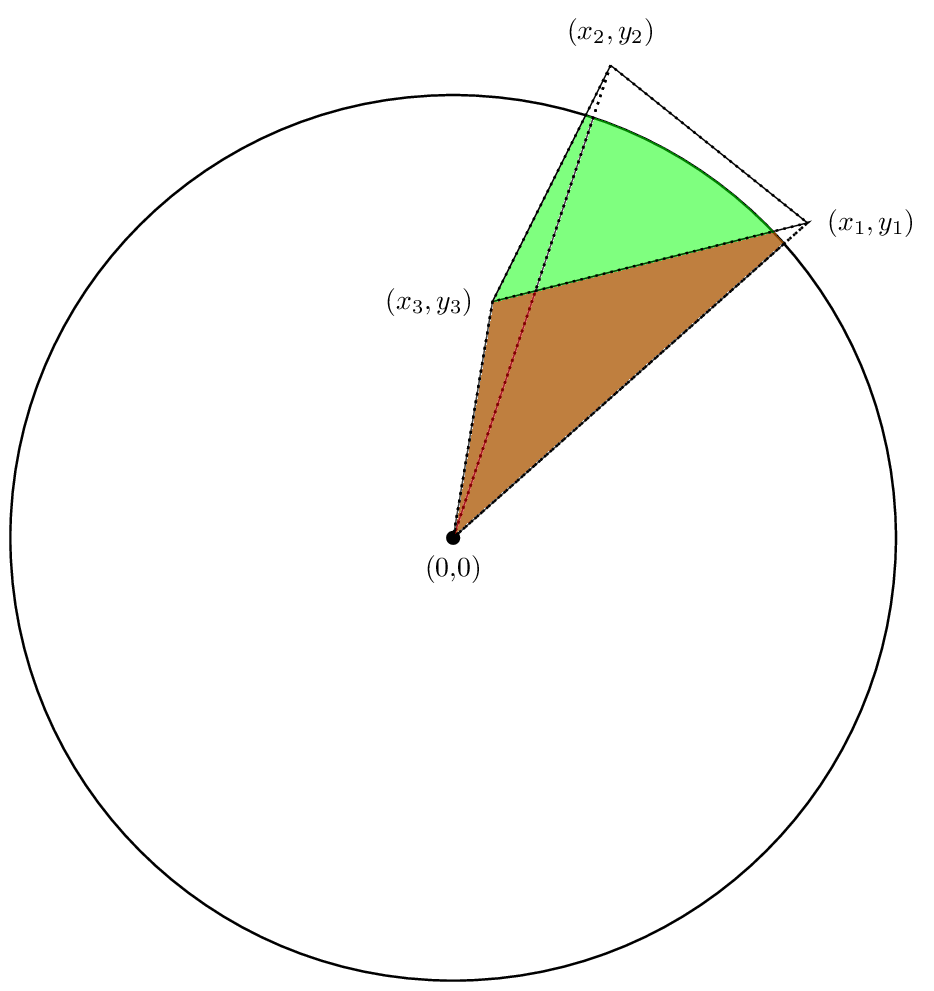
опять же, первые две области положительный в нашем случае, в то время как третий будет отрицательным. Надеюсь, что отмена будет работать так, что чистая область действительно является областью, в которой мы заинтересованы. Давайте посмотрим.

действительно, сумма областей будет областью, в которой мы заинтересованы.

опять же, мы можем дать более строгое объяснение, почему это работает. Пусть I-область, определенная пересечением, а P-многоугольник. Из предыдущего обсуждения мы знаем, что хотите вычислить Интеграл r^2dθ / 2 вокруг границы I. Однако это трудно сделать, потому что для этого требуется найти пересечение.

вместо этого мы сделали Интеграл над многоугольником. Мы интегрировали max (r,R)^2 dθ/2 по границе многоугольника. Чтобы понять, почему это дает правильный ответ, определим функцию π, которая принимает точку в полярных координатах (r,θ) к точке(max (r,R),θ). Не следует путать ссылаться на координатные функции π(r)=max (r,R) и π(θ)=θ. Затем мы интегрировали π (r)^2 dθ/2 через границу многоугольника.

с другой стороны, так как π(θ)=θ, это то же самое, что интегрирование π(r)^2 dn(θ)/2 по границе многоугольника.

теперь, делая изменение переменной, мы обнаруживаем, что получим тот же ответ, если мы интегрируем r^2 dθ/2 через границу π(P), где π(P) — образ P под π.

снова используя теорему Стокса, мы знаем, что интегрирование r^2 dθ / 2 над граница π(P) дает нам площадь π (P). Другими словами, он дает тот же ответ, что и интегрирование dxdy над π(P).

используя изменение переменной снова, мы знаем, что интегрирование dxdy над π(P) совпадает с интегрированием Jdxdy над P, где J-якобиан π.

теперь мы можем разделить Интеграл Jdxdy на две области: часть в круге и часть вне круга. Теперь π оставляет точки только в окружности, поэтому J=1 там, поэтому вклад из этого часть P-это площадь части P, которая лежит в окружности, т. е. площадь пересечения. Вторая область-это область вне круга. Там J=0, так как π сжимает эту часть до границы круга.

таким образом, то, что мы вычисляем, действительно является областью пересечения.

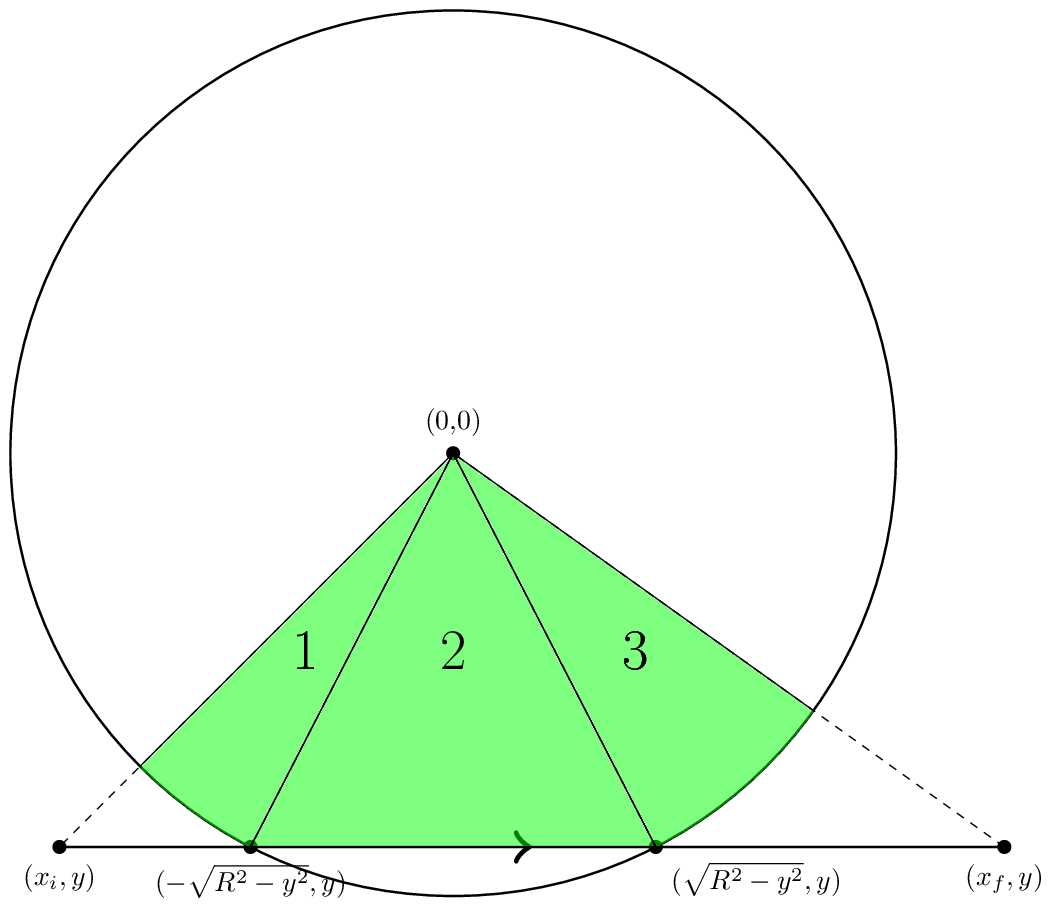
теперь, когда мы относительно уверены, что знаем концептуально, как найти область, давайте поговорим более конкретно о том, как вычислить вклад из одного сегмента. Давайте начните с рассмотрения сегмента в том, что я буду называть «стандартной геометрией». Это показано ниже.

в стандартной геометрии, край идет горизонтально слева направо. Он описывается тремя числами: xi, координата x, где начинается ребро, xf, координата x, где заканчивается ребро, и y, координата Y ребра.

теперь мы видим, что если |y /

область области 2-это только область треугольник. Однако мы должны быть осторожны со знаком. Мы хотим, чтобы область была положительной, поэтому мы скажем, что область — (xint — (- xint))y/2.

еще одна вещь, чтобы иметь в виду, что в целом, xi не должен быть меньше, чем-xint и xf не должен быть больше, чем xint.

другой случай для рассмотрения — |y / > R. Этот случай проще, потому что есть только одна часть, которая похожа на область 1 на рисунке.

теперь, когда мы знаем, как в стандартной геометрии остается только описать, как преобразовать любое ребро в стандартную геометрию.

но это всего лишь простое изменение координат. Учитывая некоторые с начальной вершиной vi и конечной вершиной vf, новый единичный вектор x будет единичным вектором, указывающим от vi до vf. Тогда xi — это просто смещение vi от центра окружности, пунктиром в x, а xf-просто xi плюс расстояние между vi и vf. Между тем y задается Клиновое произведение x со смещением vi от центра окружности.

это завершает описание алгоритма, теперь пришло время написать некоторый код. Я буду использовать Java.

во-первых, поскольку мы работаем с кругами, у нас должен быть класс circle

для полигонов я буду использовать java Shape класса. Shape С PathIterator что я могу использовать для итерации по краям многоугольника.

теперь для фактической работы. Я отделю логику итерации через ребра, помещая ребра в стандартную геометрию и т. д., от логики вычисления области, как только это будет сделано. Причина этого в том, что в будущем вы можете захотеть вычислить что-то еще, кроме или в дополнение к области, и вы хотите иметь возможность повторно использовать код, имеющий дело с итерацией по краям.

поэтому у меня есть общий класс, который вычисляет некоторое свойство класса T о нашем пересечении многоугольника.

public abstract class CircleShapeIntersectionFinder <

он имеет три статических метода, которые просто помогают вычислить геометрию:

есть два поля экземпляра, a Circle который просто держит копию круга, и currentSquareRadius , который сохраняет копию квадратного радиуса. Это может показаться странным, но класс, который я использую, на самом деле оборудован для поиска областей целого набора пересечений круга и полигона. Вот почему я имею в виду один из кругов как «текущий».

Далее идет метод вычисления того, что мы хотим вычислить:

initialize() и getValue() абстрактны. initialize() установит переменную, которая держит общую площадь в нуль, и getValue() просто вернет область. Определение для processCircleShape и

давайте второй посмотреть initializeForNewCirclePrivate быстро. Этот метод просто устанавливает поля экземпляра и позволяет производному классу сохраните любое свойство круга. Его определение

initializeForNewCircle является абстрактным, и одна реализация будет для него хранить радиус окружностей, чтобы избежать необходимости делать квадратные корни. Во всяком случае, вернемся к processCircleShape . После вызова initializeForNewCirclePrivate , мы проверяем, является ли многоугольник null (который я интерпретирую как пустой многоугольник), и мы возвращаемся, если это null . В этом случае наша вычисленная площадь будет равна нулю. Если многоугольник не null тогда мы получим PathIterator полигона. Аргумент в пользу getPathIterator метод, который я вызываю, является аффинным преобразованием, которое может быть применено к пути. Я не хочу применять один, хотя, так что я просто пройти null .

далее объявляю double[] s, которые будут отслеживать вершины. Я должен помнить первую вершину, потому что PathIterator только дает мне каждую вершину один раз, поэтому я должен вернуться после того, как он дал мне последнюю вершину, и сформировать ребро с этой последней вершиной и первой вершиной.

на currentSegment метод на следующей строке помещает следующую вершину в свой аргумент. Он возвращает код, который сообщает вам, когда он находится вне вершин. Вот почему выражение управления для моего цикла while является тем, что оно есть.

большая часть остальной части кода этого метода неинтересна логикой, связанной с итерацией через вершины. Важно то, что один раз за итерацию цикла while я вызываю processSegment и processSegment снова в конце метода для обработки края, который соединяет последняя вершина к первой вершине.

давайте посмотрим на код для processSegment :

в этом методе я реализую шаги для преобразования ребра в стандартную геометрию, как описано выше. Сначала я вычисляю segmentDisplacement смещение от начальной вершины до конечной вершины. Это определяет ось x стандартной геометрии. Я делаю раннее возвращение, если это смещение равно нулю.

далее я вычисляю длину смещения, потому что это необходимо получить X единичный вектор. Как только у меня есть эта информация, я вычисляю смещение от центра круга к начальной вершине. Точечный продукт этого с segmentDisplacement дает мне leftX который я называл xi. Тогда rightX , который я называл xf, просто leftX + segmentLength . Наконец, я делаю продукт клина, чтобы получить y как описано выше.

теперь, когда я преобразовал проблему в стандартную геометрию, с ней будет легко справиться. То есть что за processSegmentStandardGeometry метод. Давайте посмотрим на код

первый if выделяет случаи, когда y достаточно мал, чтобы ребро могло пересекать окружность. Если y большой, и нет возможности пересечения, тогда я вызываю метод для обработки этого случая. В противном случае я занимаюсь делом, где возможно пересечение.

если пересечение возможно, я вычисляю координату X пересечения, intersectionX , и я разделяю край вверх на три части, которые соответствуют областям 1, 2 и 3 приведенной выше стандартной геометрии. Сначала я обрабатываю область 1.

чтобы обработать область 1, я проверяю, если leftX действительно меньше!—54—> в противном случае не было бы области 1. Если есть область 1, то мне нужно знать, когда она закончится. Он заканчивается как минимум rightX и -intersectionX . После того, как я нашел эти X-координаты, я имею дело с этой областью, не пересекающейся.

я делаю аналогичную вещь ручки области 3.

для региона 2 я должен сделать некоторую логику, чтобы проверить это leftX и rightX на самом деле скобки некоторые области между -intersectionX и intersectionX . После нахождения области мне нужна только длина области и y , поэтому я передаю эти два числа абстрактному методу, который обрабатывает область 2.

теперь давайте посмотрим на код processNonIntersectingRegion

я просто использовать atan2 для того чтобы высчитать разницу в угле между leftX и rightX . Затем я добавляю код для борьбы с разрывом в atan2 , но это, вероятно, не нужно, потому что разрыв происходит либо при 180 градусах, либо при 0 градусах. Затем я передаю разницу в угле абстрактному методу. Наконец, у нас есть только абстрактные методы и геттеры:

теперь давайте посмотрим на класс, расширяющийся, CircleAreaFinder

в поле area для отслеживания области. initialize наборы зона до нуля, как и ожидалось. Когда мы обрабатываем непересекающийся край, мы увеличиваем площадь на R^2 Δθ/2, как мы заключили выше. Для пересекающегося края мы уменьшаем площадь на y*length/2 . Это было так, что отрицательные значения для y соответствуют положительным областям, как мы и решили.

теперь аккуратная вещь, если мы хотим отслеживать периметр, нам не нужно делать намного больше работы. Я определил AreaPerimeter класс:

и теперь мы просто нужно снова расширить наш абстрактный класс, используя AreaPerimeter как тип.

у нас есть переменная perimeter чтобы отслеживать периметр, мы помним значение radius чтобы избежать придется позвонить Math.sqrt много, и мы делегируем расчет площади нашему CircleAreaFinder . Мы видим, что формулы для периметра легко.

для справки вот полный код CircleShapeIntersectionFinder

во всяком случае, это мое описание алгоритм. Я думаю, что это хорошо, потому что это точно, и на самом деле не так много случаев, чтобы проверить.

Я почти на полтора года опоздал, но я думал, может быть, люди будут заинтересованы в здесь код что я написал, что я думаю, что это правильно. Посмотрите в функции IntersectionArea внизу. Общий подход состоит в том, чтобы снять выпуклый многоугольник, описанный окружностью, а затем иметь дело с маленькими круглыми колпачками.

предполагая, что вы говорите целочисленные пиксели, а не реальные, наивная реализация будет проходить через каждый пиксель треугольника и проверять расстояние от центра круга по его радиусу.

Это не милая формула, или особенно быстро,но она делает свою работу.

Примечание: это не тривиальная проблема, я надеюсь, что это не домашнее задание ; -)

Если у вас есть GPU в вашем распоряжении, вы можете использовать этой техника для получения количества пикселей пересечения..

Я думаю, что вы не должны аппроксимировать круг как некоторый набор треугольников, вместо этого вы можете аппроксимировать его форму многоугольником. Наивный алгоритм может выглядеть так:

преобразовать круг в многоугольник с некоторым желаемым количеством вершин.
вычислить пересечение двух полигонов (преобразованный круг и треугольник).
вычислить площадь этого пересечения.

вы можете оптимизировать этот алгоритм, объединив Шаг 2 и Шаг 3 в одной функции.

поскольку ваши фигуры выпуклые, вы можете использовать оценку площади Монте-Карло.

нарисуйте квадрат вокруг круга и треугольника.

выберите случайные точки в поле и подсчитайте, сколько падают в круге, и сколько падают как в круге, так и в треугольнике.

площадь пересечения ≅ площадь окружности * # точки в окружности и треугольник / # точки в окружности

остановить выбор точек, когда оценочная площадь не изменяется более чем на определенное количество за определенное количество раундов, или просто выбрать фиксированное количество очков на основе области коробки. Оценка площади должна сходиться довольно быстро, если одна из ваших фигур не имеет очень маленькой площади.

Примечание: вот как вы определяете, находится ли точка в треугольнике:Барицентрическими координатами

насколько точно вам нужно быть? Если вы можете приблизить круг с более простыми формами, вы можете упростить задачу. Например, было бы нетрудно смоделировать круг как набор очень узких треугольников, встречающихся в центре.

если только один из отрезков линии треугольника пересекает круг, чистое математическое решение не слишком сложно. Как только вы узнаете, когда две точки пересечения, вы можете использовать формулу расстояния, чтобы найти длину аккорда.

где c-длина хорды, r-радиус, ϑ — угол через центр, а A-площадь. Обратите внимание, что это решение нарушает, если более половины окружности выключено.

вероятно, это не стоит усилий, если вам просто нужно приближение, так как оно делает несколько предположений о том, как выглядит фактическое пересечение.

мой первый инстинкт состоял бы в том, чтобы преобразовать все так, чтобы круг был сосредоточен на происхождении, перевести треугольник в полярные координаты и решить для пересечения (или охвата) треугольника с кругом. Я еще не проработал это на бумаге, хотя это только догадка.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Как проверить принадлежность треугольника пересечению двух окружностей?

Я вот не могу понять как узнать что этот треугольник лежит на пересечении этих кругов?

P.S. Я только начал изучать с++

Вопрос задан более года назад
161 просмотр

Простой 2 комментария

У треугольника три угла, так?
И нужно, чтобы каждый из углов лежал внутри обоих кругов.
Вот и проверяйте каждую из вершин на нахождение в обоих кругах.

А у вас сейчас проверяется только одна точка.