Поток вектора электрического смещения в чем измеряется (8 видео)

Поток вектора напряженности электрического поля и электрического смещения

Как уже отмечалось, силовые линии могут начинаться или заканчиваться в какой-то точке, только если в этой точке имеется электрический заряд. Это позволяет установить связь между пространственным распределением зарядов и напряженностью создаваемого поля.

Выделим в области однородного поля Е некоторую площадку площадью S с единичным вектором нормали п к площадке (рис. 16.1). Для анализа полезно ввести новое понятие. Поток вектора напряженности электрического поля через площадку определим по формуле

где в скалярном произведении направление вектора 5 определяется нормалью п Е_п — проекция вектора напряженности электрического поля на направление нормали п. Угол а между направлением ноля и направлением нормали варьируется в пределах от 0 (поле направлено вдоль нормали) до л (ноле направлено в противоположную от нормали сторону). При этом если угол острый, то поток положителен, если тупой — отрицателен.

Поток вектора напряженности электрического ноля фактически равен (или пропорционален) числу силовых линий, проходящих через выбранную плохие. 16.1 щадку.

Несложно обобщить определение на неоднородное иоле и произвольную поверхность. В этом случае первоначально определяется ноток через бесконечно малую площадку dS:

а затем полный поток вектора напряженности электрического поля находится через интеграл по поверхности:

Аналогичным образом можно определить ноток вектора электрического смещения:

Отметим, что в случае замкнутой поверхности нормаль к поверхности принято проводить наружу. При этом поток вектора наружу получается положительным, а поток вектора внутрь — отрицательным.

Поток вектора напряженности электрического поля измеряется в Н • м 2 /Кл или В • м, поток вектора электрического смещения — в кулонах.

Содержание

Вектор электрической индукции
Вектор индукции
Связь вектора напряженности и вектора электрического смещения
Вектор D (электрическое смещение). Теорема Гаусса для вектора b
🎦 Видео

Видео:44. Электрическое поле в диэлектрике. Вектор поляризованностиСкачать

Вектор электрической индукции

Вектором электрической индукции (электрического смещения) D → называют физическую величину, определяемую по системе С И :

D → = ε 0 E → + P → , где ε 0 — электрическая постоянная, E → — вектор напряженности, P → — вектор поляризации.

Вектор электрического смещения в СНС определяется как:

Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Вектор индукции

Значение вектора D → не является только полевым, потому как он учитывает поляризованность среды. Имеется связь с объемной плотностью заряда, выражаемая соотношением:

По уравнению d i v D → = ρ видно, что для D → единственным источником будут являться свободные заряды, на которых данный вектор начинается и заканчивается. В точках с отсутствующими свободными зарядами вектор электрической индукции является непрерывным. Изменения напряженности поля, вызванные наличием связанных зарядов, учитываются в самом векторе D → .

Видео:45. Электрическое смещениеСкачать

Связь вектора напряженности и вектора электрического смещения

При наличии изотропной среды запись связи вектора напряженности и вектора электрического смещения запишется как:

D → = ε 0 E → + ε 0 χ E → = ε 0 + ε 0 χ E → = ε ε 0 E → .

Где ε – диэлектическая проницаемость среды.

Наличие D → способствует облегчению анализа поля при наличии диэлектрика. Используя теорему Остроградского-Гаусса в интегральном виде с диэлектриком, фиксируется как:

Проходя через границу разделов двух диэлектриков для нормальной составляющей, вектор D → может быть записан:

D 2 n — D 1 n = σ

n 2 → D 2 → — D 1 → = σ ,

где σ – поверхностная плотность распределения зарядов на границе диэлектриков, n 2 → — нормаль, проведенная в сторону второй среды.

Формула тангенциальной составляющей:

D 2 τ = ε 2 ε 1 D 1 τ .

Единица вектора электрической индукции измеряется в системе С И как К л м 2 .

Поле вектора D → изображается при помощи линий электрического смещения.

Определение направления и густоты идет аналогично линиям вектора напряженности. Но линии вектора электрической индукции начинаются и заканчиваются только на свободных зарядах.

Имеются пластины плоского конденсатора с зарядом q . Произойдет ли изменение вектора электрической индукции при заполненном воздухом пространстве между пластинами и диэлектрика с диэлектрической проницаемостью ε ≠ ε υ o z d .

Поле конденсатора в первом случае характеризовалось вектором смещения ε v o z d = 1 , то есть D 1 → = ε v o z d ε 0 E 1 → = ε 0 E 1 → .

Необходимо заполнить пространство между пластинами конденсатора однородным и изотропным диэлектриком. При наличии поля в конденсаторе диэлектрик поляризуется. Тогда начинают появляться связанные заряды с плотностью σ s υ на его поверхности. Создается дополнительное поле с напряженностью:

Векторы полей E → ‘ и E 1 → имеют противоположные направления, причем:

Запись результирующего поля с диэлектриком примет вид:

E = E 1 — E ‘ = σ ε 0 — σ s υ ε 0 = 1 ε 0 σ — σ s υ .

Формула плотности связанных зарядов:

Произведем подстановку σ s υ = χ ε 0 E в E = E 1 — E ‘ = σ ε 0 — σ s υ ε 0 = 1 ε 0 σ — σ s υ , тогда:

Далее выражаем из ( 1 . 6 ) напряженность поля Е . Формула принимает вид:

E = E 1 1 + χ = E 1 ε .

Отсюда следует, что значение вектора электрической индукции в диэлектрике равняется:

D = ε ε 0 E 1 ε = ε 0 E 1 = D 1 .

Ответ: вектор электрической индукции не изменяется.

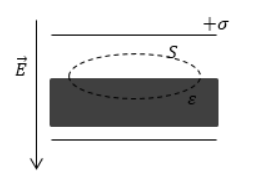
Была внесена пластина из диэлектрика с диэлектрической проницаемостью ε без свободных зарядов в зазор между разноименными заряженными пластинами. На рисунке 1 показана при помощи штриховой линии замкнутая поверхность. Определить поток электрической индукции Φ D через эту поверхность.

Рисунок 1 . Замкнутая поверхность

Формула записи потока вектора электрического смещения Φ D через замкнутую поверхность S :

Φ D = ∫ S D → · d S → .

Используя теорему Остроградского-Гаусса, можно сказать, что Φ D равняется суммарному свободному заряду, находящемуся внутри заданной поверхности. Из условия видно отсутствие свободных зарядов в диэлектрике и в имеющемся пространстве между пластинами конденсатора, а поток вектора индукции равняется нулю.

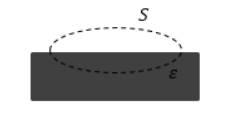
Изображена замкнутая поверхность S , проходящая с захватом части пластины изотропного диэлектрика на рисунке 2 . Поток вектора электрической индукции через нее равняется нулю, а поток вектора напряженности > 0 . Какой вывод можно сделать из данной задачи?

Рисунок 2 . Замкнутая поверхность с захватом части пластины изотропного диэлектрика

Из условия имеем, что поток вектора электрического смещения Φ D через замкнутую поверхность равняется нулю, то есть:

Если использовать теорему Остроградского-Гаусса, то значение Φ D – это суммарный свободный заряд, находящийся внутри заданной поверхности. Следует, что внутри такой поверхности отсутствуют свободные заряды:

Φ D = ∫ S D → · d S → = Q = 0 .

Имеем, что поток вектора напряженности не равен нулю, но он считается как сумма свободных и связанных зарядов. Отсюда вывод – диэлектрик содержит связанный заряды.

Ответ: свободные заряды отсутствуют, а связанные есть, причем с положительной их суммой.

Видео:Билет №02 "Теорема Гаусса"Скачать

Вектор D (электрическое смещение). Теорема Гаусса для вектора b

Напряженность электростатического поля зависит от свойств среды (от с). Кроме того, вектор напряженности Е на границе диэлектриков претерпевает скачкообразное изменение. Введем для описания электрического поля системы зарядов с учетом поляризационных свойств диэлектриков вспомогательный вектор, использование которого во многих случаях упрощает изучение поля в диэлектриках.

Внутри диэлектрика поле определяется и сторонними, и связанными зарядами. Поэтому, исходя из теоремы Гаусса для вектора напряженности в вакууме (12.11) и учитывая величину плотности нескомпенсированного связанного заряда р’ в диэлектрике, запишем:

По теореме Гаусса для вектора поляризации (13.5)

Тогда имеем, что

где вектором электрического смещения (электрической индукции) называется вектор

Для изотропного диэлектрика с учетом формулы (13.3) получаем

Единица вектора электрического смещения в СИ — кулон на метр в квадрате (Кл/м 2 ).

Вектор D описывает электростатическое поле, создаваемое сторонними зарядами в вакууме, но при таком их распределении в пространстве, какое имеется при наличии диэлектрика.

Аналогично линиям напряженности можно ввести линии электрического смещения. Направление и густота линий вектора электрического смещения определяются так же, как и для вектора напряженности Е.

Согласно уравнению (13.11), теорема Гаусса в дифференциальной форме для вектора D имеет вид